Properties of Quartics

Abstract. This portfolio investigates properties of quartics, with

a special eye toward their points of inflection. As a result of this
investigation we shall see the emergence of the Golden Ratio.

which is the same as solving

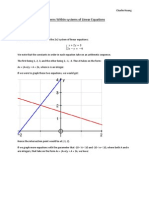
Let us begin with the quartic defined

by the function f (x) = x4 8x3 + 18x2
12x + 24. As f 00 (x) = 12x2 48x + 36 =
12(x 1)(x 3), we conclude that on the
graph of y = f (x) there are two points
of inflection, namely the points Q(1, 23)
and R(3, 15). The straight line passing
through Q and R meets the graph of
y = f (x) at two other points, which we
call P and S. This is indicated in the
graph below:

x4 8x3 + 18x2 8x 3 = 0.
Since we already know that x = 1, 3 are
solutions, two synthetic divisions will reduce to problem of finding the remaining
solutions to that of solving a quadratic
equation. The synthetic division is displayed below:
1

Place quartic1 here

3

1 8
18 8 3
1 7 11
3
1 7
11
3
3 12 3
1 4 1

As a result of the above, we see that

the x-coordinates of the remaining points
are the two (irrational) solutions of the
2
quadratic equation
x 4x1 = 0. These
solutions are 2 5. We therefore let

P = P (2 + 5, f (2 + 5)), and

R = R(2 5, f (2 5)).

The coordinates of P and S are very

easily arrived at, as follows. First, note
that the line passing through Q and R has
slope 4, from which it follows that this
line has equation y 15 = 4(x 3). We
write this as y = 4x+27 which allows us
to compute the points of intersection with
the graph of y = f (x). The x-coordinates
Our investigation continues by considof such points are obtained by solving the ering the ratios P Q : QR : RS. Notice
equation
that we really dont need to compute the
distances between the points themselves
(using the distance formula); rather, by
4
3
2
x 8x + 18x 12x + 24 = 4x + 27, similar triangles (see diagram below) we
1

need only compute the distances between

the x-coordinates of these points.

Place quartic4 here

Place quartic2 here

In order to find the x-coordinates of

the remaining two points of intesection,
we solve the equation
Thus, we let xP , xQ , xR , and xS be
x4 2x3 = x,
the x-coordinates of the points P, Q, R,
and S, respectively. Therefore, the ratio which is the same as solving
P Q : QR : RS is simply the ratio
x4 2x3 + x = 0.
|xP xQ | : |xQ xR | : |xR xS |.
That is, we get the ratio

51:2:

Since x4 2x3 +x = x(x3 2x2 +1), reduce

the problem to that of solving a quadratic
by a synthetic division by 1:
1

5 1.

1 2
0
1
1 1 1
1 1 1

This says that x4 2x3 +x = x(x1)(x2

5 1 yields x 1); the zeros of the quadratic are precisely the Golden
Ratio and
its algebraic

1+ 5
1 5
conjugate:
and 2 . It follows,
2

therefore
that
the
ratio P Q : P R : RS
1+ 5
1:
: 1.
is the ratio
2

1 5
1 5
:1:
.
2
2
While it may seem premature, we nonormalize by dividing
tice that the middle factor is precisely the As above, we

1 5
,
which now produces the
through
by
Golden Ratio, which is the positive solu2
2
tion of the quadratic equation x x1 = equivalent ratio
0. The next obvious step is to try another

1+ 5
example to see if the same result obtains.
1:
: 1,
2
We take up the ostensibly simpler exactly as in the case above!
quartic polynomial g(x) = x4 2x3 . As
We formalize the above as a conjecg 00 (x) = 12x2 12x = 12x(x 1), we
see that the points of inflection are at the ture.
points (0, 0) and (1, 1). The relevant be- Conjecture. Let f (x) be a quartic
havior is depicted below:
polynomial and assume that The graph
Dividing all quantities by
the equivalent ratio

of y = f (x) has two distinct points, Q factor; we accomplish this via a synthetic
and R of inflection. Then the straight division:
line passing through Q and R meets the
a 1 2a
0
a3
graph of y = f (x) in two other distinct
2
a a a3
points P and S;furthermore P Q = RS
1 a a2
QR
1+ 5
, the Golden Ratio.
and
=
2
PQ
and so the x-coordinates of P and S are
We analyze the general case along the the solutions of the quadratic equation
following lines. Assume that the graph
y = f (x) of the quartic polynomial f (x)
x2 ax a2 = 0.
has two points of inflection Q and R. By

1
These
solutions
are
x
=
(a

a
5),
translating this graph in the x and y di2
from
which
we
conclude
that
the
ratio
rections if necessary, we may assume that
Q is the origin and that R has coordi- P Q : QR : RS is given by
nates R(a, f (a)), for some real number a.

Therefore, for some constant b we have

1
1
(a

a
5)
:
a
:
(a
+
a
5).
2
2
that
00
f (x) = bx(x a).
Finally, upon normalizing so that the first
Integrating twice we conclude that f (x) factor is unity, we arrive at the ratio
must have the form

1+ 5
1:
: 1,
2
f (x) = 1 b(x4 2ax3 + cx),
12

exactly as in the previous specific cases!

for an arbitrary real constants c. (Note
This concludes the proof of the above
that since f (0) = 0, there is only one
conjecture.
nonzero constant of integration.) This
1
says that R = R(a, 12
b(a4 + ca)), and so
As a postscript we mention that there
the slope of the straight line joining Q and
1
R is 12
b(a3 + c). From this we conclude are two other classes of quartics that dont
fall under the perview of the above conthat the equation of this straight line is
jecture. The first class of quartics will
1
y = 12
b(a3 + c)x.
have a second derivative having a multiple (hence a double) zero. Such a zero
Next, we proceed to find the remainwill not afford a point of inflection point
ing two points P and S of intersection of
as the graph of the quartic will not change
the above line with the graph of the quarits concavity through this point (the sectic. The x-coordinates of this intersection
ond derivative wont change sign). The
are given by the solutions of the equation
second class of quartics will have an irreducible (over the reals) quadratic; again,
4
3
3
1
1
there can be no points of inflection on the
b(x 2ax + cx) = 12 b(a + c)x,
12
graph.
which simplifies to the equation
With this in mind, we now can state
the following theorem.
x(x3 2ax2 + a3 ) = 0.
Since a is also a root of the above equa- Theorem. Let f (x) be a quartic polynotion, we can factor the cubic polynomial mial having a point of inflection Q. Then

there must be a second point of inflec- R, and S according to their x-coordinates

tion R. If l is the straight line pass- (least to greatest), then P Q = RS and
ing through Q and R, then, in addition to

QR
1+ 5
these points, l must meet the graph of y =
=
,
f (x) in two other distinct points P and
PQ
2
S. Finally, if we order the points P , Q, the Golden Ratio.