Circles and Construction

Circles and Construction

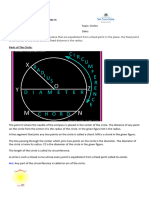
A circle is a simple shape of Euclidean geometry that is the set of points in the plane that are equidistant from a given point, the centre. The distance between any of the points and the centre is called the radius. A circle is a simple closed curve which divides the plane into two regions: an interior and an exterior. In everyday use, the term "circle" may be used interchangeably to refer to either the boundary of the figure, or to the whole figure including its interior; in strict technical usage, the circle is the former and the latter is called a disk. A circle can be defined as the curve traced out by a point that moves so that its distance from a given point is constant. A circle may also be defined as a special ellipse in which the two foci are coincident and the eccentricity is 0. Circles are conic sections attained when a right circular cone is intersected by a plane perpendicular to the axis of the cone. Napoleon's problem is a famous compass construction problem. In it, a circle and its center are given. The challenge is to divide the circle into four equal arcs using only a compass. Napoleon was known to be an amateur mathematician but it is not known if he either created or solved the problem. Napoleon's friend the Italian mathematician Lorenzo Mascheroni introduced the limitation of using only a compass (no straight edge) into geometric constructions. But actually, the challenge above is easier than the real Napoleon's problem, consisting in finding the center of a given circle with compass alone. The following sections will describe solutions to both problems, and the proofs that they work. Know More About :- Whole Number Subtraction

Math.Edurite.com

Page : 1/3

Construction :- Let (C) be the circle, whose centre is to be found. Let A be a point on (C). A circle (C1) centered at A meets (C) at B and B'. Two circles (C2) centered at B and B', with radius AB, cross again at point C. A circle (C3) centered at C with radius AC meets (C1) at D and D'. Two circles (C4) centered at D and D' with radius AD meet at A, and at O, the sought center of (C). Note: for this to work the radius of circle (C1) must be neither too small nor too large. More precisely, this radius must be between half and double of the radius of (C): if the radius is greater than the diameter of (C), (C1) will not intersect (C); if the radius is shorter than half the radius of (C), point C will be between A and O and (C3) will not intersect (C). Dividing a given circle into four equal arcs given its centre :- Centred on any point X on circle C, draw an arc through O (the centre of C) which intersects C at points V and Y. Do the same centred on Y through O, intersecting C at X and Z. Note that the segments OV, OX, OY, OZ, VX, XY, YZ have the same length, all distances being equal to the radius of the circle C. Now draw an arc centred on V which goes through Y and an arc centred on Z which goes through X; call where these two arcs intersect T. Note that the distances VY and XZ are times the radius of the circle C. Put the compass radius equal to the distance OT ( times the radius of the circle C) and draw an arc centred on Z which intersects the circle C at U and W. UVWZ is a square and the arcs of C UV, VW, WZ, and ZU are each equal to a quarter of the circumference of C.

Read More About :- Properties of Rational Number

Math.Edurite.com

Page : 2/3

ThankYou

Math.Edurite.Com