First Order Nonlinear Equations

The most general nonlinear first order ordinary differential equation we could imagine would be of the form Ft, yt, y v t = 0. 1

In general we would have no hope of solving such an equation. A less general nonlinear equation would be one of the form y v t = Ft, yt, 2

but even this more general equation is often too difficult to solve. We will consider then, equations of the form y v t = Fyt. 3

Equation (3) is said to be an autonomous differential equation, meaning that the nonlinear function F does not depend explicitly on t. The equation (2) is nonautonomous because F does contain explicit t dependence. The equations, y v t = yt 2 and y v t = yt 2 + t 2 ,

are examples of autonomous and nonautonomous equations, respectively. We will consider some examples of nonlinear first order equations first and then state some general principles that will make it clear why autonomous equations are easier to deal with than nonautonomous ones. We will first recall a few of the properties that we have observed about linear problems. We saw in several examples that solutions to linear problems tend to be smooth functions, even when the coefficients and forcing term are discontinuous. The only thing that seemed to lead to a blow up or singularity in the solution (i.e., a point where the solution becomes undefined) was a singularity in a coefficient or forcing term. Thus, when there are no singularities in the inputs of the problem, there will be no singularities in the solution and the solution will satisfy the equation for all t. Another way to say this is that there are no spontaneous singularities in the solution to a linear ODE. Solution singularities can only result from input singularities. In addition, the general solution of a linear equation is a 1-parameter family of functions which satisfies the equation for every choice of the parameter and which contains all possible solutions to the equation. That is, there are no solutions to the equation that cant be written in the form of the general solution for some choice of the parameter. We have not yet proved this last statement but will prove it later. When an initial condition is combined with the equation, it follows that there is a unique value of the parameter in the general solution that causes the initial condition to be satisfied. Thus the initial value problem will always have a unique solution. Summarizing these features of linear problems, we have

t t t

no spontaneous singularities 1-parameter family of general solutions initial value problem has a unique solution

We will now give some examples that will show that for nonlinear problems, none of these things need be true. Example 1 Consider the initial value problem, y v t = yt 2 , Writing leads to ?yt ?1 = t ? C 0 , or yt = Then given by, y0 = A 1 . C0 ? t C 0 = 1/A and the solution of the initial value problem is y0 = A > 0.

X dy = X dt 2
y

implies A . 1 ? At

yt =

Note that this function has a singularity at t = 1/A so that, even though there is nothing in the equation to suggest it, the solution develops a spontaneous singularity. Example 2 Consider the initial value problem, y v t = 2 yt , Writing we find yt = t ? C 0 or yt = t ? C 0 2 . The functions yt solve the differential equation for each value of the constant C 0 . However, this cannot be called the general solution of the equation since the zero function yt = 0 also solves the equation but the zero function does not equal t ? C 0 2 for any value of C 0 . Notice also that yt 0 = 0, t 0 > 0.

dy = X dt, 2 yt

yt = t ? t 0 2 solves the intial value problem, while at the same time, for every t 1 > t 0 , the functions yt = 0 if t 0 < t < t 1 t > t1

t ? t 1 2 if

also solve the initial value problem. These two examples illustrate that solutions to nonlinear differential equations may behave quite differently from solutions to linear problems. This does not mean that all nonlinear problems are necessarily badly behaved, it only means that we should not assume that we cannot suppose that they are necessarily as well behaved as linear problems. Autonomous First Order Equations The simplest possible model for population growth is the equation P v t = kPt, P0 = P 0

where the constant k denotes the growth rate of the population. If k is positive, the population described by this equation grows rapidly to infinity while, if k is negative, it decays steadily to zero. In an effort to make a more realistic model for growth of population size, we may suppose that k is not a constant but depends on P. In particular, if we suppose kP = rP K ? Pt for some positive constants r, P K , then we obtain the autonomous equation P v t = r P K ? PtPt, P0 = P 0 . 4

Here FP = r P K ? PtPt does not depend explicitly on t. It is not difficult to solve this differential equation but we are going to see that it is possible to completely understand the behavior this equation predicts without actually solving the equation. In fact, it is generally harder to see the predicted behavior from the solution than from the qualitative analysis we are going to describe. We begin by determining if the equation has any critical points. These are values P D of P such that FP D = 0, (which means that if there is any time t = T D at which PT D = P D , then Pt = P D for all t T D ). Equation (4) has two critical points, namely P = 0 and P = P K . In addition, for any solution curve starting at P 0 with 0 < P 0 < P K , we have P v 0 = r P K ? P 0 P 0 > 0, which means the curve starts out with P increasing. In fact, we will show that P is increasing along this solution curve for all t > 0. The argument goes like this. If there is a point on this solution curve where P is not increasing, then there has to be a time t 0 > 0 where P v t 0 = 0 (i.e., if P is decreasing, it has to first stop increasing). Since this is a point on a solution curve, if P v t 0 = 0 then either Pt 0 = 0 or else Pt 0 = P K . But Pt 0 = 0 is not possible since P started at P 0 with 0 < P 0 < P K , and P has been increasing since then. On the other hand, Pt 0 = P K is not possible either since if t 0 is the first time after t = 0 where Pt 0 = P K , then Pt < P K for t < t 0 which would imply P v t 0 > 0. But this contradicts equation (4) which asserts that P v t 0 = 0 if Pt 0 = P K . The only

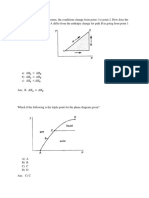
remaining possibility is that a solution curve which originates at P 0 with 0 < P 0 < P K , must approach the horizontal asymptote P = P K , increasing steadily as t tends to K. In the same way, we can argue that any solution curve that originates at P 0 with P 0 > P K , must approach the horizontal asymptote P = P K , from above, decreasing steadily as t tends to K. A plot showing three different solution curves is shown below.

If we define a asymptotically stable critical point P = P D to mean a value P D such that FP D = 0, and such that any for trajectory, Pt, originating at P0 near P D , it follows that Pt P D as t K. A critical point for which the distance between Pt and P D increases as t K, even for P0 arbitrarily near P D , is said to be unstable. Equation (4) has critical points at P = 0 and P = P K . T By examining the figure above, we see that the critical point at P = 0 is unstable, while the critical point at P = P K is asymptotically stable. Now we state some general results about autonomous nonlinear equations. If we consider the equation y v t = Fyt, then
1. 2. 3. 4.

the critical points of (5) are the values y D for which Fy D = 0 the critical point, y D is stable if F v y D < 0 the critical point, y D is unstable if F v y D > 0 distinct trajectories of (5) can never cross

Here 1 is just the definition of critical point. Points 2 and 3 can be proved in a similar manner so let us prove 3. The figure below shows an F(y) having a zero at y D (hence y D is a critical point for (5)) with F v y D > 0. Since the derivative of F at y D is positive and Fy D = 0,

it follows that at any y > y D , we have Fy > 0 which implies, in turn through (5) that y v t is positive (i.e., y is increasing when y > y D . Similarly, at any y < y D , we have Fy < 0 which implies, in turn through (5) that y v t is negative (i.e., y is decreasing when y < y D . Then solution curves of (5) which originate near y D move away from y D rather than towards it. This is what it means for the critical point to be unstable. Point 2 is proved by a similar argument.

To see that point 4 must be true suppose that y = y 1 t and y = y 2 t are two different solutions of (5) whose graphs cross at some time t 0 . To say the graphs cross at t = t 0 means that y 1 t 0 = y 2 t 0 , and y v1 t 0 y v2 t 0 .; i.e., the graphs go through the same point but have different slopes there. But y 1 t 0 = y 2 t 0 y v1 t 0 = Fy 1 t 0 = Fy 2 t 0 = y v2 t 0 , hence the slopes cannot be different. This contradiction shows that solution curves are either identical or else they never cross. We say that the family of solution curves is coherent.