Escolar Documentos
Profissional Documentos
Cultura Documentos
Integrales Complejas
Enviado por
Lin Lin Alata MayhuireTítulo original
Direitos autorais
Formatos disponíveis
Compartilhar este documento
Compartilhar ou incorporar documento
Você considera este documento útil?
Este conteúdo é inapropriado?
Denunciar este documentoDireitos autorais:
Formatos disponíveis
Integrales Complejas
Enviado por
Lin Lin Alata MayhuireDireitos autorais:
Formatos disponíveis
Semana 14 - Clase 36/13 Tema 2: Variable Compleja
Integraci on en Variable Compleja
1. Integrales complejas
Como siempre, luego de denir la derivada, construimos el concepto de integral a partir de la
suma de Riemann. Esto es
S
n
=
n
j=1
f(
j
)(z
j
z
j1
) si n |z
j
z
j1
| 0 lm
n
n
j=1
f(
j
)(z
j
z
j1
) =
_
z
2
z
1
dz f(z)
Es decir, que si el lm
n
S
n
existe, entonces corresponde con la denicion de la integral.
1.1. Algunas propiedades
Es claro que esta integral es, necesariamente, una integral de lnea, ya que z tiene dos dimen-
siones
_
z
2
z
1
dz f(z) =
_
z
2
z
1
(dx + idy) (u(x, y) + iv(x, y))
=
_
x
2
,y
2
x
1
,y
1
(u(x, y)dx v(x, y)dy) + i
_
x
2
,y
2
x
1
,y
1
(v(x, y)dx + u(x, y)dy) (1)
con lo cual transformamos una integral compleja en una suma de integrales reales, pero necesitamos
denir el contorno a traves del cual vamos de z
1
= x
1
+ iy
1
z
2
= x
2
+ iy
2
La integracion compleja tendra las propiedades acostumbradas
_
C
dz (f(z) + g(z)) =
_
C
dz f(z) +
_
C
dzg(z)
_
C
dz Kf(z) = K
_
C
dz f(z) con K una constante real o compleja
_
b
a
dz f(z) =
_
a
b
dz f(z)
_
b
a
dz f(z) =
_
m
a
dz f(z) +
_
b
m
dz f(z)
_
C
dz |f(z)| ML donde M = max |f(z)| y L la longitud de C
Esta ultima propiedad es importante porque permite establecer cotas a las integrales complejas sin
tener que evaluarlas. De la denicion de integral es casi inmediata la demotracion
lm
n
n
j=1
f(
j
)z
j
=
_
z
2
z
1
dz f(z)
j=1
f(
j
)z
j
j=1
|f(
j
)| |z
j
| M
n
j=1
|z
j
| ML
Donde hemos utilizado que |f(
j
)| M y que la suma de los intervalos z
j
= z
j
z
j1
es la longitud
L del recorrido C. Es claro que tomando lmites a ambos miembros obtendremos
_
C
dz f(z)
_
C
dz |f(z)| ML.
Hector Hernandez / Luis N u nez 1 Universidad de Los Andes, Merida
Semana 14 - Clase 36/13 Tema 2: Variable Compleja
1.2. Un par de ejemplos
Por ejemplo, evaluemos la integral compleja f(z) = z
1
a lo largo de diferentes contornos, tal
y como se ilustran en la gura 1
un circuito cerrado a lo largo de una circunferencia de radio R
_
dz z
1
_
d(Re
i
) R
1
e
i
= i
_
2
0
d = 2i
siguiendo una semicircunferencia desde (R, 0) (R, 0). Esto es
_
z
2
=(R,0)
z
1
=(R,0)
dz z
1
=
_
(R,)
(R,0)
d(Re
i
) R
1
e
i
= i
_
0
d = i
siguiendo dos lneas rectas entre los puntos (R, 0) (0, R) (R, 0). En este caso, pro-
cedemos utilizando la expresion cartesiana para los n umeros complejos. Para ello, vamos a
parametrizar z = z(t) para (R, 0) (0, R) y z = z(s) cuando (0, R) (R, 0). Veamos
_
z
3
=(R,0)
z
1
=(R,0)
dz z
1
=
_
z
2
=(0,R)
z
1
=(R,0)
dz z
1
+
_
z
3
=(0,R)
z
2
=(0,R)
dz z
1
para cada una de las integrales se cumple, respectivamente, que
z = (1 t)R + itR con 0 t 1 z = sR + i(1 s)R con 0 s 1
con lo cual
_
z
2
=(R,0)
z
1
=(R,0)
dz
z
=
_
1
0
1 + i
(1 t) + it
dt +
_
1
0
1 i
s + i(1 s)
ds
procedemos entonces con la primera de las integrales
_
1
0
1 + i
(1 t) + it
dt =
_
1
0
1 + i
(1 t) + it
(1 t) it
(1 t) it
dt =
_
1
0
2t 1
1 2t + 2t
2
dt + i
_
1
0
dt
1 2t + 2t
2
es decir
_
1
0
1 + i
(1 t) + it
dt =
1
2
ln(1 2t + 2t
2
)
1
0
+ i arctan(2t 1)|
1
0
= 0 +
i
2
=
i
2
la segunda integral tambien tendra el mismo resultado, con lo cual:
_
z
2
=(R,0)
z
1
=(R,0)
dz
z
= i , el mismo resultado que a traves del arco de circunferencia !
Hector Hernandez / Luis N u nez 2 Universidad de Los Andes, Merida
Semana 14 - Clase 36/13 Tema 2: Variable Compleja
Figura 1: Integrales complejas y circuitos
Es interesante notar que si regresamos al punto (R, 0) a traves del contorno: (R, 0) (0, R)
(R, 0) la integral cerrada se anula, no as cuando nos regresamos a traves el arco complementario
de circunferencia. En pocas palabras, como se esperaba, el valor de las integrales de camino, para
algunas funciones, dependeran del camino seleccionado. Mas adelante veremos a cuales funciones
correspondera un mismo valor de la integral cerrada, independientemente del circuito que uno elija.
Queda como ejercicio al lector repetir los mismos pasos anteriores para el caso de f(z) = (z
)
1
.
Otro ejemplo ilustrativo lo constituye
_
dz
(z z
0
)
n+1
,
esto es:
_
2
0
Rie
i
d
R
n+1
e
i(n+1)
=
i
R
n
_
2
0
d e
in
_
_
_
n = 0 :
_
2
0
d = 2i
n = 0 :
i
R
n
_
2
0
d (cos n isen n) = 0
donde hemos utilizado la forma polar z z
0
Re
i
e integrado a lo largo de una circunferencia de
radio R centrada en z = z
0
.
Hector Hernandez / Luis N u nez 3 Universidad de Los Andes, Merida
Semana 14 - Clase 36/13 Tema 2: Variable Compleja
Figura 2: Regiones en el plano complejo
2. Teorema Integral de Cauchy
2.1. El Teorema y las Regiones
El teorema integral de Cauchy es uno de los dos teoremas basicos en la teora de funciones
de variable compleja. Este teorema considera que si f(z) es analtica en una region simplemente
conexa, R, en su contorno C y su derivada f
(z) existe y es contnua en esta region
1
, entonces la
circulacion a lo largo de cualquier contorno cerrado C se anula. Esto es
_
C
dz f(z) = 0
Antes que nada, y como parte de ese adiestramiento en lenguaje, precisaremos que queremos decir
(que quieren decir los matematicos) con regiones simplemente conexa y m ultiplemente conexa
Una region simplemente conexa es aquella que no tiene huecos, o dicho de una manera mas
precisa y elegante, en la cual una curva puede ser reducida (encogida) a un punto sin salir de la
region R. En la gura 2 cuadrante Ia se muestra una region simplemente conexa y en los cuadrantes
Ib y Ic regiones multiplemente conexas. Estas dos ultimas guras clarican este concepto. Es decir,
una region m ultiplemente conexa es aquella que no es simplemente conexa y con eso queremos decir
que tiene huecos, o lo que es lo mismo existen curvas que no se pueden reducir a puntos en la
region.
1
Esta ultima condicion no es necesaria, pero la demostraci on del Teorema se torna mucho m as sosticada, y
referimos al lector a los libros especializados, vale decir a las referencias: Churchill R. V. y a Knopp K.
Hector Hernandez / Luis N u nez 4 Universidad de Los Andes, Merida
Semana 14 - Clase 36/13 Tema 2: Variable Compleja
Tal y como hemos comentado la demostracion rigurosa del Teorema de Cauchy esta fuera de
los alcances de estas notas, pero algo se puede hacer si invocamos el Teorema de Stokes (o uno
de los Teoremas de Green en el plano) que vimos cuando estudiamos analisis vectorial. Con ello
recordamos la ecuacion (1), entonces
_
z
2
z
1
dz f(z) =
_
x
2
,y
2
x
1
,y
1
(u(x, y)dx v(x, y)dy) + i
_
x
2
,y
2
x
1
,y
1
(v(x, y)dx + u(x, y)dy)
El Teorema de Stokes nos dice que
_
R
dxdy
_
p
x
+
q
y
_
=
_
C
(pdy qdx)
con lo cual, si una vez mas suponemos f(z) = u(x, y)+iv(x, y) y dz = dx+idy, entonces tendremos
que
_
C
(udx vdy)+i
_
C
(vdx + udy) =
_
R
dxdy
_
(v)
x
+
(u)
y
_
+i
_
R
dxdy
_
(u)
x
+
(v)
y
_
= 0
y acto seguido, como f(z) es analtica, invocamos las condiciones de Cauchy Riemann y es inmediato
ver que se anula la integral de circulacion.
2.2. Algunas observaciones y el Teorema de Morera
De la anterior demostracion del Teorema de Cauchy Riemann emergen algunas observaciones:
La primera es la insistencia de que la condicion que la derivada f
(z) existe y es contnua en
esta region no es necesaria.
La segunda es que el Teorema de Cauchy Riemann, es valido tambien para regiones m ulti-
plementes conexas. Consieremos una region como la descrita en la gura 2 cuadrante II, es
claro que podemos circular la integral en los siguientes contornos
_
C
dz f(z) =
_
ABDEAFGHFA
dz f(z)
_
ABDEA
dz f(z)+
_
AF
dz f(z)+
_
FGHF
dz f(z)+
_
FA
dz f(z) = 0
y como
_
AF
dz f(z) =
_
FA
dz f(z), entonces:
_
ABDEA
dz f(z) +
_
FGHF
dz f(z) = 0
_
C
1
dz f(z) +
_
C
2
dz f(z) = 0
con lo cual se nota que para regiones m ultiplemente conexas, a pesar que las circulaciones son
opuestas, el observador que circula por C
1
y C
2
siempre tiene la region R a su izquierda.
Siguiendo con la reexion anterior, podemos invertir el sentido de la circulacion en el contorno
C
2
con lo cual
_
C
1
dz f(z)
_
C
2
dz f(z) = 0
_
C
1
dz f(z) =
_
C
2
dz f(z)
Es decir, que si f(z) es analtica en una region R, da igual cualquier recorrido por las fronteras
de una region y el valor de la integral permanecera inalterado.
Hector Hernandez / Luis N u nez 5 Universidad de Los Andes, Merida
Semana 14 - Clase 36/13 Tema 2: Variable Compleja
Mas a un este resultado puede extenderse a regiones con n huecos de tal forma que, tal y como
ilustra en en la gura 2 cuadrante III
_
C
1
dz f(z) =
n
j=1
_
C
j
dz f(z)
Con lo cual estamos armando que, dada una region que contiene un n umero nito ( nume-
rable ?) n de singularidades, la integral a lo largo del contorno que encierra la region R es
equivalente a la suma de las integrales que encierran cada una de las n singularidades.
Enunciaremos sin demostracion el Teorema de Morera
2
, tambien conocido como el teorema inverso
de Cauchy.
Teorema de Morera: Si una funcion f(z) es continua en una region Rencerrada por un contorno
C y
_
C
dz f(z) = 0 entonces f(z) es analtica en R
Ejemplo: Considere la funcion denida en una region R
f(z) =
1
z z
0
con
_
z
0
fuera de la region R
z
0
dentro de la region R
Si z
0
esta fuera de la region, entonces f(z) esa analtica en R, con lo cual el Teorema de
Cauchy implica que
_
C
dz f(z) = 0
Si z
0
esta dentro de la region, entonces f(z) no es analtica en R por cuanto existe una
singularidad z = z
0
. Si consideramos C el contorno que bordea a R, como una circunsferencia
centrada en z = z
0
y otra circunsferencia que aisla a z
0
con un radio |z z
0
| = (esta
situacion se ilustra en la gura 3 cuadrante I). Entonces, si hacemos z z
0
= z = e
i
el
Teorema de Cauchy implica
_
C
dz
z z
0
=
_
dz
z z
0
=
_
2
0
ie
i
d
e
i
= i
_
2
0
d = 2i
3. F ormula integral de Cauchy
El ejemplo de la seccion anterior nos lleva a una de las expresiones mas utiles e importantes del
analisis complejo: La Formula Integral de Cauchy la cual dice que si f(z) es analtica en una region
R encerrada por un contorno C y consideramos un punto z = z
0
contenido en esa region, entonces
1
2i
_
C
f(z) dz
z z
0
= f(z
0
) .
2
Pueden consultar la demostraci on en el Arfken,Weber: Mathematical Methods for Physicists
Hector Hernandez / Luis N u nez 6 Universidad de Los Andes, Merida
Semana 14 - Clase 36/13 Tema 2: Variable Compleja
Figura 3: Circulaciones y Polos
Para probar esta armacion supongamos, una vez mas un circuito en encierra al polo z = z
0
(ver
gura 3, cuadrante II). Con lo cual, como f(z) es analtica en esa region, el Teorema de Cauchy
nos garantiza
1
2i
_
C
f(z) dz
z z
0
=
1
2i
_
f(z) dz
z z
0
si z z
0
= re
i
,
esto implica que
1
2i
_
2
0
f(z
0
+ re
i
)rie
i
d
re
i
=
1
2
_
2
0
f(z
0
+ re
i
)d ,
si hacemos r 0 tendremos que
1
2i
_
C
f(z) dz
z z
0
=
1
2i
_
f(z) dz
z z
0
= lm
r0
1
2
_
2
0
f(z
0
+re
i
)d =
1
2
_
2
0
lm
r0
f(z
0
+re
i
)d = f(z
0
)
Observaciones Surgen tambien observaciones al respecto
Obvio que es valido para regiones m ultiplemente conexas y es facil demostrarlo. Se lo dejamos
al lector como ejercicio.
Si reacomodamos la expresion para la forma integral podemos hacer en esa formula es valida
para todo z
f(z) =
1
2i
_
C
f() d
z
Hector Hernandez / Luis N u nez 7 Universidad de Los Andes, Merida
Semana 14 - Clase 36/13 Tema 2: Variable Compleja
Mas a un veremos que es facil generalizar esta formula para derivadas de funciones, vale decir
f
(n)
(z
0
) =
n!
2i
_
C
f(z) dz
(z z
0
)
n+1
Veamos con el caso mas sencillo y demostremos que para n = 1
f
(z
0
) =
1
2i
_
C
f(z)dz
(z z
0
)
2
f
(z
0
) = lm
h0
f(z
0
+ h) f(z
0
)
h
= lm
h0
1
2i
_
C
f(z)
h
_
1
z z
0
h
1
z z
0
_
dz
tal y como se muestra en la gura 3, cuadrante III tenemos que
f
(z
0
) = lm
h0
_
1
2i
_
C
f(z) dz
(z z
0
h)(z z
0
)
_
=
1
2i
_
C
f(z) dz
(z z
0
)
2
Pero mucho mas interesante hubiera sido derivar respecto a una constante. Este truco implica
que
f(z) =
1
2i
_
C
f() d
z
f
(n)
(z) =
1
2i
_
C
n
z
n
_
f()
z
_
d =
n!
2i
_
C
f() d
( z)
n+1
(2)
Esta formula es muy util para calcular integrales. Considere, por ejemplo la siguiente integral
I =
_
C
e
2
d
( + 1)
4
2i
3!
f
(3)
(1) con f(z) = e
2z
I =
8i
3
e
2
donde hemos supuesto que el contorno C encerraba el punto z = 1, porque de otro modo la funcion
e
2z
(z + 1)
4
sera analtica y la integral se anulara por el Teorema de Cauchy.
Ejemplos: 1.- Evaluar
I =
1
2i
_
C
e
z
z 2
dz , para los entornos: C: |z| = 3 y C: |z| = 1 .
El entorno |z| = 3 contiene en su interior al punto z
0
= 2, esto implica que:
1
2i
_
C
e
z
z 2
dz = e
2
.
Para el entorno |z| = 1, vemos que el punto z
0
= 2 no esta contenido en ese entorno, esto signica
que el integrando es una funcion analtica en toda la region. Por lo tanto:
1
2i
_
C
e
z
z 2
dz = 0.
2.- Evaluar
I =
_
C
1
z
2
+ 4
dz , para los entornos: C
1
: |z 1| = 2 , C
2
: |z| = 3 y C
3
: |z + i| = 2 .
Hector Hernandez / Luis N u nez 8 Universidad de Los Andes, Merida
Semana 14 - Clase 36/13 Tema 2: Variable Compleja
La integral puede ser escrita de la siguiente manera:
I =
_
C
1
(z + 2i)(z 2i)
dz .
Para el contorno |z 1| = 2, tenemos que este contiene en su interior al punto z
0
= 2i. Si escribimos
la integral como
I =
_
C
1
z+2i
z 2i
dz ,
la funcion 1/(z + 2i) es analtica dentro de C
1
y entonces por el teorema de Cauchy
I =
_
C
1
z+2i
z 2i
dz = 2i
_
1
4i
_
=
2
.
Consideremos ahora el contorno |z| = 3. Este contorno contiene en su interior a los puntos 2i y
2i. Podemos trazar dos contornos adicionales, de radio alrededor de cada punto, entonces:
_
C
1
z
2
+ 4
dz =
_
C
(2i)
1
z
2
+ 4
dz +
_
C
(2i)
1
z
2
+ 4
dz
=
_
C
(2i)
1
z+2i
z 2i
dz +
_
C
(2i)
1
z2i
z + 2i
dz
= 2i
_
1
z + 2i
_
z=2i
+ 2i
_
1
z 2i
_
z=2i
= 2i
_
1
4i
_
+ 2i
_
1
4i
_
= 0 .
Finalmente, para el contorno |z +i| = 2 se tiene que este contiene al punto z
0
= 2i. Repitiendo
lo que hicimos en el primer caso tenemos:
I =
_
C
1
z2i
z + 2i
dz
la funcion 1/(z 2i) es analtica dentro de C
3
y entonces por el teorema de Cauchy
I =
_
C
1
z2i
z + 2i
dz = 2i
_
1
4i
_
=
2
.
Hector Hernandez / Luis N u nez 9 Universidad de Los Andes, Merida
Você também pode gostar
- Laplaciano EsfericasDocumento7 páginasLaplaciano EsfericasGorky Limachi CcapaAinda não há avaliações
- Problemas Resueltos DivergenciaDocumento10 páginasProblemas Resueltos DivergenciafansbeatlesAinda não há avaliações
- Unidad 5: Integración MúltipleDocumento29 páginasUnidad 5: Integración MúltipleE Ben Hernandez Chavez69% (13)
- Metodos Numericos para Raices Complejas (Newton-Raphson)Documento7 páginasMetodos Numericos para Raices Complejas (Newton-Raphson)Saul Ayala RodriguezAinda não há avaliações
- Vale Oro Problemas Resueltos TodoDocumento222 páginasVale Oro Problemas Resueltos TodoManuel100% (4)
- Informe, Curva Del Ventilador - Geraldyne, RenzzoDocumento11 páginasInforme, Curva Del Ventilador - Geraldyne, RenzzoGeraldyne Figueredo AriasAinda não há avaliações
- Integrales de SuperficieDocumento8 páginasIntegrales de SuperficieBenji Martell BernardoAinda não há avaliações
- An Alisis Matem Atico en Variable ComplejaDocumento31 páginasAn Alisis Matem Atico en Variable ComplejaacomillaAinda não há avaliações
- Teorema de Green, Stokes y de La Divergencia y Su Aplicación en La Física.Documento8 páginasTeorema de Green, Stokes y de La Divergencia y Su Aplicación en La Física.Carlos Ivan VilladiegoAinda não há avaliações
- Clse 3 RelatividadDocumento34 páginasClse 3 RelatividadChristiam Rossi GonzalesAinda não há avaliações
- Apgeom 3Documento36 páginasApgeom 3pbchantaAinda não há avaliações
- Funciones Complejas de Variable Compleja.Documento13 páginasFunciones Complejas de Variable Compleja.leorefasolAinda não há avaliações
- Integrales ComplejasDocumento10 páginasIntegrales ComplejasNuri AlonsoAinda não há avaliações
- Métodos Matemáticos II Febrero 2023 Segunda SemanaDocumento10 páginasMétodos Matemáticos II Febrero 2023 Segunda SemanaPaquito MAinda não há avaliações
- Sanabria - Generalización de La Carta de SmithDocumento11 páginasSanabria - Generalización de La Carta de SmithArashi AoiAinda não há avaliações
- Lectura Fundamental 5Documento16 páginasLectura Fundamental 5jhon jairo marinez rojasAinda não há avaliações
- Int MultDocumento39 páginasInt MultEsteban QuinteroAinda não há avaliações
- Apuntes Matematica Superior 2014Documento112 páginasApuntes Matematica Superior 2014GEORGE AR�MIS VASQUEZ LLANOSAinda não há avaliações
- Integral PDFDocumento37 páginasIntegral PDFCristoferPonteRojasAinda não há avaliações
- Integrales Triples - Regiones Generales, Sustituciones y Aplicaciones.Documento28 páginasIntegrales Triples - Regiones Generales, Sustituciones y Aplicaciones.Macarena FuicaAinda não há avaliações
- Cap 11Documento18 páginasCap 11ManuelGarcíaAinda não há avaliações
- Ejercicios Resueltos Variable Compleja 1Documento36 páginasEjercicios Resueltos Variable Compleja 1ronald_c07Ainda não há avaliações
- Semana15-Calculo3 - Teorema de GreenDocumento16 páginasSemana15-Calculo3 - Teorema de GreenZamuel CRamosAinda não há avaliações
- Examen 11 MayobDocumento4 páginasExamen 11 MayobIvan Prieto OlivaAinda não há avaliações
- Teorema de La DivergenciaDocumento10 páginasTeorema de La DivergenciaAlexis CruzAinda não há avaliações
- Restricciones de Grupos FuchsianosDocumento56 páginasRestricciones de Grupos FuchsianosCarlos Martinez100% (1)
- Unidad 5 Integracion MultipleDocumento27 páginasUnidad 5 Integracion Multiplelyon100% (2)
- MMTF Tarea31Documento9 páginasMMTF Tarea31Juan Manuel González López100% (1)
- Resolucion SchrodingerDocumento4 páginasResolucion SchrodingerVafdg Pdert AokiuAinda não há avaliações
- Calculo 3 Integrales Triples IteradasDocumento8 páginasCalculo 3 Integrales Triples IteradasCielo CastilloAinda não há avaliações
- Apuntes Ie305Documento91 páginasApuntes Ie305José Carlos Cortés Mora100% (1)
- Integraci On en El Plano Complejo: 4.1. Funciones Complejas de Variable RealDocumento28 páginasIntegraci On en El Plano Complejo: 4.1. Funciones Complejas de Variable RealAnonymous zBSE9MAinda não há avaliações
- Integral ComplejaDocumento17 páginasIntegral ComplejaelhacedordelimasAinda não há avaliações
- MetIGrJun2011Sem2Sol 3Documento3 páginasMetIGrJun2011Sem2Sol 3Jorge SánchezAinda não há avaliações
- Resumen02 PDFDocumento8 páginasResumen02 PDFGustavo EscalanteAinda não há avaliações
- Problemas Variable ComplejaDocumento11 páginasProblemas Variable Complejasimha_86100% (1)
- Integrales TriplesDocumento16 páginasIntegrales TriplesPiero Lermo100% (1)
- Teoremas Variable Compleja PDFDocumento10 páginasTeoremas Variable Compleja PDFmichi garcilazoAinda não há avaliações
- Centro de MasaDocumento54 páginasCentro de MasaRafael Carvajal MillánAinda não há avaliações
- HW 01Documento4 páginasHW 01Martin Alejandro Arredondo GonzalezAinda não há avaliações
- Varcomi 2019-20 Apuntes8 Tma-ResiduosDocumento10 páginasVarcomi 2019-20 Apuntes8 Tma-ResiduosNelson CarbajalAinda não há avaliações
- Guía Teórica Lagrange e Integrales MultiplesDocumento7 páginasGuía Teórica Lagrange e Integrales MultiplesFrank OsunaAinda não há avaliações
- Complejos DistanciaDocumento10 páginasComplejos DistanciaEmiliano NavarroAinda não há avaliações
- 2 - Metodo de Separacion de Variables Ec Poisson PDFDocumento15 páginas2 - Metodo de Separacion de Variables Ec Poisson PDFRamses Jerez NicurcarAinda não há avaliações
- Integral Doble 0910Documento37 páginasIntegral Doble 0910Edwin C. AbregúAinda não há avaliações
- Ejercicios de Integrales y Ecuaciones Integrales-DiferencialesNo EverandEjercicios de Integrales y Ecuaciones Integrales-DiferencialesAinda não há avaliações
- La ecuación general de segundo grado en dos y tres variablesNo EverandLa ecuación general de segundo grado en dos y tres variablesAinda não há avaliações
- Transformación de radón: Revelando patrones ocultos en datos visualesNo EverandTransformación de radón: Revelando patrones ocultos en datos visualesAinda não há avaliações
- Analisis de Agua de CalderasDocumento13 páginasAnalisis de Agua de Calderasari78Ainda não há avaliações
- Manual de Procedimientos para Análisis de Aguas y Efluentes IndustrialesDocumento174 páginasManual de Procedimientos para Análisis de Aguas y Efluentes IndustrialesFortunato Seijas50% (2)
- Tratamiento de Aguas de ProcesoDocumento70 páginasTratamiento de Aguas de ProcesoLin Lin Alata MayhuireAinda não há avaliações
- Limites de Control en Sistemas de Vapor y Condensado Agosto 2014Documento4 páginasLimites de Control en Sistemas de Vapor y Condensado Agosto 2014Lin Lin Alata MayhuireAinda não há avaliações
- CRISTALIZACIONDocumento5 páginasCRISTALIZACIONLin Lin Alata MayhuireAinda não há avaliações
- Medidores de Area VariableDocumento39 páginasMedidores de Area VariableAlex Uscanga Lara0% (1)
- Caudalimetro UltrasonicoDocumento11 páginasCaudalimetro UltrasonicoLin Lin Alata MayhuireAinda não há avaliações
- TrabajoDocumento34 páginasTrabajoLin Lin Alata MayhuireAinda não há avaliações
- Helado TESIS PDFDocumento97 páginasHelado TESIS PDFWalter WalterAinda não há avaliações
- Guia de MatlabDocumento59 páginasGuia de MatlabOscar VargasAinda não há avaliações
- UNIDAD 3 Proyecto de Empresa Gerencia 1Documento11 páginasUNIDAD 3 Proyecto de Empresa Gerencia 1Lin Lin Alata MayhuireAinda não há avaliações
- Unidad #1 y 2 Aspectos Conceptuales de Empresa, Promocvion Empresarial GERENCIA 1Documento88 páginasUnidad #1 y 2 Aspectos Conceptuales de Empresa, Promocvion Empresarial GERENCIA 1Lin Lin Alata MayhuireAinda não há avaliações
- AdafDocumento1 páginaAdafLin Lin Alata MayhuireAinda não há avaliações
- 1489 PapaDocumento33 páginas1489 PapaLin Lin Alata MayhuireAinda não há avaliações
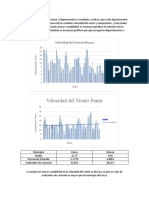
- VelocidadDocumento1 páginaVelocidadLin Lin Alata MayhuireAinda não há avaliações
- Taller 1 FQDocumento2 páginasTaller 1 FQAlejandra Lopez RuizAinda não há avaliações
- ChristiannDocumento7 páginasChristiannChristian CalderonAinda não há avaliações
- Plan Estudios Ing Mecatrónica 2021Documento1 páginaPlan Estudios Ing Mecatrónica 2021daniela paola munoz bustosAinda não há avaliações
- Taller de Nivelación #1 - MatemáticasDocumento4 páginasTaller de Nivelación #1 - MatemáticasPascual Jose HerreraAinda não há avaliações
- Taller de Fisica de Decimo Periodo IIDocumento2 páginasTaller de Fisica de Decimo Periodo IIBreidys FortichAinda não há avaliações
- Examen Final de ESTADISTICA GENERALDocumento4 páginasExamen Final de ESTADISTICA GENERALKAROL STEPHANNIE SERRANO MAMANIAinda não há avaliações
- Calculo CurvasDocumento4 páginasCalculo CurvasKevin Vargas JulcamoroAinda não há avaliações
- Me1 2021 Guia1Documento2 páginasMe1 2021 Guia1Nahuel NietoAinda não há avaliações
- FisicaDocumento2 páginasFisicaDaniel Alejandro GilAinda não há avaliações
- Busqueda y RescateDocumento34 páginasBusqueda y RescateAlexander Gutierres Hernandez100% (1)
- Perdidas en Carga A Conductos A PresionDocumento9 páginasPerdidas en Carga A Conductos A PresionDaniel Mosquera LunaAinda não há avaliações
- Tema2 Estadistica Descriptiva UnivarianteDocumento16 páginasTema2 Estadistica Descriptiva UnivarianteSamuel HerediaAinda não há avaliações
- Modulo 1 - SituacionesDocumento13 páginasModulo 1 - SituacionesJesús Emmanuel Chuquispuma SauñeAinda não há avaliações
- Silabus de Circuitos ElectricosDocumento5 páginasSilabus de Circuitos ElectricosAlex Coronado VarelaAinda não há avaliações
- Probabilidad WeibullDocumento4 páginasProbabilidad WeibullJeisson Alejandro Luque GuacanemeAinda não há avaliações
- Curriculo Byn 2018Documento1 páginaCurriculo Byn 2018Yolanda Marinez PuertoAinda não há avaliações
- Fórmula de HerónDocumento7 páginasFórmula de HerónElías Arias EstebanAinda não há avaliações
- Cilindro y CircunferenciaDocumento8 páginasCilindro y CircunferenciaKristopher Angel CQAinda não há avaliações
- Estructuras y Sistemas Constructivos, Zapatas Aisladas, NTN Ings. CivilesDocumento16 páginasEstructuras y Sistemas Constructivos, Zapatas Aisladas, NTN Ings. CivilesMauri Rivera GonzalesAinda não há avaliações
- Grupo 4 - Exposición 1Documento8 páginasGrupo 4 - Exposición 1NESTOR HUINCHO LEONAinda não há avaliações
- Razones y ProporcionesDocumento34 páginasRazones y ProporcionesSaavedra Carranza LidiaAinda não há avaliações
- Escala de Corrientes en El Multímetro DigitalDocumento2 páginasEscala de Corrientes en El Multímetro DigitalAlex Jesus Coronado SaucedoAinda não há avaliações
- Cálculo Del Caudal de La Bomba: Bombas Triplex de LodoDocumento3 páginasCálculo Del Caudal de La Bomba: Bombas Triplex de LodoMilton SilesAinda não há avaliações
- 59 - 21 - Mundial - 2020 - ES IdeDocumento32 páginas59 - 21 - Mundial - 2020 - ES IdemarioAinda não há avaliações
- Modulo Semana 5Documento80 páginasModulo Semana 5eeggalAinda não há avaliações
- HT Semana 6 WaDocumento2 páginasHT Semana 6 WaAlexander Santiago PorrasAinda não há avaliações
- Serie 1 Problemas 2020Documento5 páginasSerie 1 Problemas 2020OlyAlcantarAinda não há avaliações
- Magnitudes Eléctricas. Ley de Ohm: Material Resistividad ( M)Documento7 páginasMagnitudes Eléctricas. Ley de Ohm: Material Resistividad ( M)De La Cruz Vasquez JeffersonAinda não há avaliações