Escolar Documentos
Profissional Documentos
Cultura Documentos
AlgebraTema5Teo (09 10) PDF
Enviado por
water125Título original
Direitos autorais
Formatos disponíveis
Compartilhar este documento
Compartilhar ou incorporar documento
Você considera este documento útil?
Este conteúdo é inapropriado?
Denunciar este documentoDireitos autorais:
Formatos disponíveis
AlgebraTema5Teo (09 10) PDF
Enviado por
water125Direitos autorais:
Formatos disponíveis
Tema 5
Diagonalizaci on de Endomorsmos
5.1 Introducci on
En este tema estudiaremos la diagonalizaci on de endomorsmos. La idea central de este proceso es determinar, para una aplicaci on lineal f : E E , en qu e situaciones es posible construir una base del espacio vectorial E de tal manera que la matriz asociada a f en dicha base sea una matriz diagonal. Recordemos algunos conceptos estudiados en temas anteriores: Sea B = { e1 , . . . , en } es una base de E , entonces se construye de manera directa la matriz: M = M (f ; B, B ) sin m as que colocar como columnas a las coordenadas de las im agenes de los vectores de B : f ( e1 ), . . . , f ( en ), en la propia base B . De esta manera, para un vector cualquiera: u = (x1 , . . . , xn )B , con f ( u) = (y1 , . . . , yn )B , tendremos: M.X = Y siendo X e Y las matrices columna de las coordenadas xi e yj respectivamente. en E , con matriz de cambio de base A, es decir: Si se introduce una nueva base B =X P.X , =Y P.Y
entonces, tal y como se demostr o en temas anteriores: = M (f ; B, B ) M , = A1 .M.A M
(si es que existe) obtendremos y la cuesti on que nos ocupa es determinar en qu e base B sea diagonal. que M 57
58
DIAGONALIZACION
, son matrices semejantes si Denici on: Se dice que dos matrices cuadradas, M y M = P 1 M P . existe una matriz invertible P tal que M Desde este punto de vista, la idea fundamental comentada puede re-escribirse en la forma: Buscamos determinar, dada una matriz M cuadrada, si es semejante o no a una matriz diagonal. Ejemplo: Dado el endomorsmo f : R3 R3 denido por f (x, y, z ) = (4x + y + 2z, 2x +
y 2z, x y + z ) respecto de la base can onica, calcular la matriz B = {e1 (1, 1, 1), e2 (1, 0, 1), e3 (1, 1, 0)} de R3 . Calculamos la matriz de cambio de base y aplicamos la f ormula: 1 1 1 1 = A1 M A = A= 1 0 1 M 0 1 1 0 0 asociada a f en la base
0 2 0
0 0 3
Hemos obtenido por tanto que la matriz asociada a f en las nuevas bases es diagonal. Alternati y expresarlas en la propia vamente, podr amos haber calculado las im agenes de los vectores de B B , de la siguiente forma: f (1, 1, 1) = 1(1, 1, 1) 1 0 0 = M f (1, 0, 1) = 2(1, 0, 1) 0 2 0 f (1, 1, 0) = 3(1, 1, 0) 0 0 3
Denici on: Sea E un espacio vectorial real de dimensi on n y sea f : E E un endomorsmo de V . Un vector e E , no nulo, e = 0, es un vector propio (o autovector) de f si existe un escalar tal que f ( e) = e. El escalar recibe entonces el nombre de valor propio o autovalor de f correspondiente al vector propio e. Es evidente la raz on por la cual se ha excluido el vector nulo de la denici on anterior. Dado que f es una aplicaci on lineal, se vericar a siempre que f ( 0) = 0, por lo que el vector nulo ser a, de alguna manera, un vector propio de todos los endomorsmos, eso s , sin un autovalor concreto asignado. Proposici on 1. El valor propio asociado a un vector propio es u nico.
Dem. Consideremos dos autovalores 1 y 2 para el autovector e: } f ( e) = 1 e 1 e = 2 e (1 2 ) e = 0 1 = 2 pues e = 0 f ( e) = 2 e de modo que el autovalor es u nico.
Proposici on 2. El conjunto de todos los vectores propios asociados a un mismo autovalor (incluyendo en dicho conjunto al vector nulo) es un subespacio vectorial de E. V = { e E / f ( e) = e} { 0}
DIAGONALIZACION
59
La demostraci on es trivial. Si razonamos brevemente con estas dos proposiciones, resulta evidente que dados dos autovalores 1 y 2 , 1 = 2 , de un endomorsmo, entonces: 0}. V1 V2 = { Por otro lado, ambas proposiciones conducen tambi en de manera directa a demostrar que dos autovectores correspondientes a diferentes autovalores son linealmente independientes. Este hecho se generaliza sin dicultad en la siguiente proposici on: Proposici on: Sean e1 , . . . , er vectores propios del endomorsmo f de E , asociados a los autovalores 1 , . . . , r , respectivamente. Si i = j , i = j , entonces el sistema S = { e1 , . . . , er } es libre. Denici on: Se dene multiplicidad geom etrica d del autovalor como la dimensi on del subespacio de vectores propios V . El subespacio V puede caracterizarse de la siguiente forma: e V f ( e) = e f ( e) e = 0 (f Id)( e) = 0 e Ker(f Id) siendo Id el endomorsmo identidad, es decir: Id( e) = e, e E. Tenemos entonces: V = Ker(f Id) , d = dim Ker(f Id)
Denici on: Un endomorsmo f del espacio vectorial E es diagonalizable si existe una base BD de E formada por vectores propios de F . Es evidente que esta denici on concuerda perfectamente con lo expuesto al principio de la secci on. Si la base BD es de la forma: BD = { e1 , e2 , ..., ed1 , ed1 +1 , ed1 +2 , ..., ed1 +d2 , ..., }
1 2
donde los d1 primeros autovectores tienen como autovalor asociado a 1 , y as sucesivamente con los dem as. Tendremos entonces: f ( e1 ) = 1 e1 + 0 e2 + ... + 0 ed1 + 0 ed1 +1 + ... f ( e2 ) = 0 e1 + 1 e2 + ... + 0 ed1 + 0 ed1 +1 + ... ... = ... f ( ed1 ) = 0 e1 + 0 e2 + ... + 1 ed1 + 0 ed1 +1 + ... f ( ed1 +1 ) = 0 e1 + 0 e2 + ... + 0 ed1 + ed1 +1 + ... ... = ...
60 D = M (f ; BD , BD ) = 1 ... ... (d1 ) ... 1 2 ... ... (d2 ) ... 2 ...
DIAGONALIZACION
= diag (1 , ..., 1 , 2 , ..., 2 , ...) ... ...
5.2
Polinomio caracter stico
Tal y como se ha comentado anteriormente, si e es un autovector de f con autovalor , entonces: e Ker(f Id). Buscamos ahora una manera de determinar cu ales son los autovectores y autovalores de un endomorsmo dado. Fijada una base B en E , sea M = M = M (f ; B, B ) la matriz asociada a f en dicha base y sea X la matriz columna de coordenadas de un vector propio cualquiera e en dicha base. Tendremos entonces: M X = X (M I ) X = 0 Si se escribe expl citamente la expresi on (M I ) X = 0: (a11 ) x1 + a12 x2 +... a21 x1 + (a22 ) x2 + . . . . . .. . . . . . an1 x1 + an2 x2 a1n xn a2n xn . . . = 0 = 0 . . .
+ . . . (ann ) xn = 0
observamos que no es m as que un sistema de n ecuaciones con n inc ognitas para cada valor concreto del escalar . Dado que se trata de un sistema homog eneo, ser a siempre compatible (admite trivialmente la soluci on nula, ). La existencia de autovectores est a por tanto ligada al hecho de que el sistema sea compatible indeterminado, y por tanto, aplicando el Teorema de Rouch e-Frobenius el rango de la matriz de coecientes ha de ser necesariamente menor que n. Es decir: det (M I ) = 0 Esta ecuaci on recibe el nombre de ecuaci on caracter stica del endomorsmo f (demostraremos a continuaci on que no depende de la base tomada, tan s olo de f ) y sus soluciones son los valores de para los cuales existen autovectores de f , es decir son los u nicos autovalores posibles del endomorsmo. Denici on: Se dene el polinomio caracter stico del endomorsmo f (o equivalentemente de su matriz asociada M ) como: Pc () = det (M I )
DIAGONALIZACION
61
Proposici on: La condici on necesaria y suciente para que sea autovalor del endomorsmo f es que sea ra z de la ecuaci on caracter stica. Recordemos ahora que un polinomio de grado n tiene siempre n ra ces en el cuerpo de los n umeros complejos, pero no es as si nos restringimos al cuerpo de los n umeros reales, como es nuestro caso. Si suponemos que un caso concreto todas las ra ces son reales, tendremos entonces: Pc () = ( 1 )1 ( 2 )2 .... ( r )r donde i , i = 1, . . . , r, denota la multiplicidad algebraica de cada ra z del polinomio. Obviamente: 1 + . . . + r = n. Propiedades del polinomio caracter stico 1. El polinomio caracter stico de un endomorsmo f es invariante bajo los cambios de base. Por tanto el polinomio caracter stico no depende de la base elegida. 2. Si i es autovalor del endomorsmo f entonces: ki es autovalor del endomorsmo kf . i k es autovalor del endormorsmo f kId. Si f es un isomorsmo, 1/i es autovalor del isomorsmo inverso f 1 .
n n i es autovalor del endomorsmo f
Propiedad 3. Si i es una ra z de Pc () con multiplicidad algebraica i y multiplicidad geom etrica di , se cumple que: 1 di i Ejemplo: Calculemos los valores y vectores propios de las siguientes matrices:
1 2 0 A = 1 3 1 0 1 1 5 0 B= 0 3 2 0 4 0 1
Matriz A: Se tiene que pc () = (1 )( 2)2 . Los autovalores son 1 = 1 y 2 = 2 con multiplicidades algebraicas 1 = 1 y 2 = 2 respectivamente. Los subespacios propios ser an: V1 =1 = ker(A I ) = (1, 0, 1) y V2 =2 = ker(A 2I ) = (2, 1, 1), y por ello las multiplicidades geom etricas son: d1 = 1 y d2 = 1. Matriz B : Se tiene que pc () = ( 1)( 3)2 . Los autovalores son 1 = 1 y 2 = 3 con multiplicidades algebraicas 1 = 1 y 2 = 3 respectivamente. Los subespacios propios son: V1 =1 = ker(A I ) = (1, 0, 1) y V2 =3 = ker(A 3I ) = (2, 0, 1), (0, 1, 0), y por ello las multiplicidades geom etricas son: d1 = 1 y d2 = 2.
62
DIAGONALIZACION
5.3
Teorema de Diagonalizaci on
Teorema: Dado un endomorsmo f End(E ), con E un K-espacio vectorial de dimensi on n, entonces f es diagonalizable si y s olo si, a) Su polinomio caracter stico tiene n ra ces en K, esto es, 1 + 2 + ... + p = n b) Para cualquier autovalor i se verica que la multiplicidad algebraica y la geom etrica coinciden di = i Demostraci on: Tenemos que demostrar los dos sentidos de la armaci on anterior:
f es diagonalizable Condiciones a) y b). Si f : E e es diagonalizable entonces existe una base BD en la que la matriz asociada D es diagonal, por ello, D = M (f ; BD , BD ) = diag{1 , ..., 1 , 2 , ..., 2 , ..., p , ..., p }
1 2 p
El polinomio caracter stico ser a entonces: Pc () = (1 )1 (2 )2 ... (p )p , de modo que obviamente: 1 + 2 + ... + p = n. Observemos en particular el autovalor 1 : d1 = dim Ker(M 1 I ) = n rang (M 1 I ) = = n rang diag {0, ..., 0, 2 , ..., 2 , ..., p , ..., p } =
1 2 p
= n (n 1 ) = 1 De manera an aloga se procede para el resto de autovalores, de manera que se concluye: di = i . Condiciones a) y b) f es diagonalizable. Ya hemos visto que si queremos encontrar una base en la que la matriz M sea diagonal, esta debe estar formada por los autovectores de f . Es obvio los subespacios propios pertenecen al espacio vectorial E , Vi = Ker (M i I ) E . Se demostr o tambi en que los Vi eran disjuntos, de manera que la suma de estos subespacions ser a directa. Por tanto: V1 V2 ... Vp V
d1 d2 dp
y como di = i y adem as 1 + 2 + ... + p = n, entonces tambi en d1 + d2 + ... + dp = n, y en denitiva: V1 V2 ... Vp = E En consecuencia, puede elegirse una base del espacio E formada por autovectores, y as f es diagonalizable. Q.E.D.
Você também pode gostar
- 15 Años Tiene Mi AmorDocumento2 páginas15 Años Tiene Mi Amorwater125Ainda não há avaliações
- Porque Te VasDocumento2 páginasPorque Te Vaswater125Ainda não há avaliações
- Me Cole en Una FiestaDocumento1 páginaMe Cole en Una Fiestawater125Ainda não há avaliações
- GuantanameraDocumento1 páginaGuantanamerawater125Ainda não há avaliações
- La Garota de Ipanema Piano AcordsDocumento1 páginaLa Garota de Ipanema Piano Acordswater125Ainda não há avaliações
- Dossier Grease El Musical PDFDocumento6 páginasDossier Grease El Musical PDFwater125Ainda não há avaliações
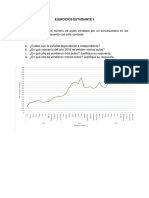
- Calculo Diferencial Tarea 1 Ejercicios Estudiante 3Documento17 páginasCalculo Diferencial Tarea 1 Ejercicios Estudiante 3Edinson Medina RiveraAinda não há avaliações
- La Función AfínDocumento3 páginasLa Función AfínPedroOlivarAinda não há avaliações
- Matlab Man - 01Documento18 páginasMatlab Man - 01Diego NareaAinda não há avaliações
- CDI2 Cap 5Documento16 páginasCDI2 Cap 5Johnny HuincahueAinda não há avaliações
- 2do - Quiz - Calculo II - Intento2Documento4 páginas2do - Quiz - Calculo II - Intento2Raul Junco100% (3)
- Cuadernillo Recuperación TALLER MATE IV 2023 EPOANADocumento10 páginasCuadernillo Recuperación TALLER MATE IV 2023 EPOANASAUL RAZIEL TOBON SILVAAinda não há avaliações
- Transformadas EspecialesDocumento5 páginasTransformadas EspecialesMiguel Navarrete SotoAinda não há avaliações
- Actividad 7Documento4 páginasActividad 7camilaAinda não há avaliações
- Funcion de HeavisideDocumento22 páginasFuncion de Heavisidealeb4119Ainda não há avaliações
- Evidencia U2Documento27 páginasEvidencia U2Juan Genaro Parra RosalesAinda não há avaliações
- Soluciones 3Documento11 páginasSoluciones 3JozeluAinda não há avaliações
- Integrales ImpropiasDocumento55 páginasIntegrales ImpropiasIsmael MillanAinda não há avaliações
- Ángulo Mitad para Quinto Grado de SecundariaDocumento2 páginasÁngulo Mitad para Quinto Grado de Secundariaelber527Ainda não há avaliações
- AlgebraDocumento63 páginasAlgebraDiego BendezuAinda não há avaliações
- Tablas WeigelDocumento30 páginasTablas WeigelSantiago EstrellaAinda não há avaliações
- Conjunto de UnicidadDocumento50 páginasConjunto de UnicidadSantiago SanguchoAinda não há avaliações
- 27-04-2021 Cálculo GA. Integrales de Productos de Senos y Cosenos de Ángulos Diferentes. Integrales DefinidasDocumento13 páginas27-04-2021 Cálculo GA. Integrales de Productos de Senos y Cosenos de Ángulos Diferentes. Integrales DefinidasdanielaAinda não há avaliações
- S13.s1 - VOLUMEN POR CORTEZAS Y CAPAS CILINDRICAS PDFDocumento7 páginasS13.s1 - VOLUMEN POR CORTEZAS Y CAPAS CILINDRICAS PDFFredy Hilaridad chaisaAinda não há avaliações
- EJERCICIOS. DerivadasDocumento10 páginasEJERCICIOS. DerivadasLuz EscobarAinda não há avaliações
- Grupos AlgebraicosDocumento3 páginasGrupos AlgebraicosJosé Carlos Chávez Sandoval100% (1)
- X Matrices UniDocumento2 páginasX Matrices UniSoujiro Seta0% (1)
- CálculoDocumento8 páginasCálculoRomina Hilen Lerma NavaAinda não há avaliações
- TP 3 Límite y Continuidad-ADMINISTRACIÓNDocumento10 páginasTP 3 Límite y Continuidad-ADMINISTRACIÓNSandri DeltinAinda não há avaliações
- Funciones HiperbólicasDocumento12 páginasFunciones HiperbólicasJorgeAlexanderBenaventeTiconaAinda não há avaliações
- 1-2-Calculo en Una Variable-1618 10s Vig 15Documento5 páginas1-2-Calculo en Una Variable-1618 10s Vig 15Mac PepeAinda não há avaliações
- Ejercicios 2.5Documento18 páginasEjercicios 2.5Daniel Jose Berrios RivasAinda não há avaliações
- Hoja de Trabajo #12 - Valores y Vectores Propios-1Documento2 páginasHoja de Trabajo #12 - Valores y Vectores Propios-1Alejo Paredes VarasAinda não há avaliações
- Algebra III Clase 03 ESFMDocumento6 páginasAlgebra III Clase 03 ESFMLuis Angel Rivera CruzAinda não há avaliações
- Tabla de Valores de Funciones TrigonometricasDocumento3 páginasTabla de Valores de Funciones TrigonometricasRichard Morales MendezAinda não há avaliações
- Función de Dos o Más VariablesDocumento3 páginasFunción de Dos o Más VariablesJose Jimenez0% (1)