Escolar Documentos
Profissional Documentos
Cultura Documentos
WWW - Enggnotes.In: Concepts of Mechanical Vibrations
Enviado por
Trigger DineshTítulo original
Direitos autorais
Formatos disponíveis
Compartilhar este documento
Compartilhar ou incorporar documento
Você considera este documento útil?
Este conteúdo é inapropriado?
Denunciar este documentoDireitos autorais:
Formatos disponíveis
WWW - Enggnotes.In: Concepts of Mechanical Vibrations
Enviado por
Trigger DineshDireitos autorais:
Formatos disponíveis
Concepts of Mechanical Vibrations
Draft 1, 10/04/06
Introduction
Consider the single degree of freedom (dof) system in Figure 1 that is usually introduced in a first course in physics or ordinary differential equations. There, k is the spring constant, or stiffness, and m is the mass, and c is a viscous damper. If the system is subjected to a horizontal force, say f(t), then Newtons law of motion leads to the differential equation of motion in terms of the displacement as a function of time, x(t): m d2x /dt2 + c dx / dt + k x(t) = f(t) which requires the initial conditions on the displacement, x(0), and velocity, v(0) = dx / dt(0). When there is no external force and no damping, then it is called free, undamped motion, or simple harmonic motion (SHM): m d2x /dt2 + k x(t) = 0.
[k 2 m] a sin (t) = 0, or [k 2 m] = 0.
Natural Frequencies
A spring and a mass interact with one another to form a system that resonates at their characteristic natural frequency. If energy is applied to a spring-mass system, it will vibrate at its natural frequency. The level of a general vibration depends on the strength of the energy source as well as the damping inherent in the system. The natural frequency of an undamped (c = 0), free (f=0), single spring-mass system is given by the following equation:
Figure 1 A spring-mass-damper system
Page 1 of 2. Copyright J.E. Akin. All rights reserved.
.E
= 2 Fn = (k/m)
This is solved for the circular frequency, , which is related to the so called natural frequency, Fn, by F n = / 2 .
The usual simple harmonic motion assumption is x(t) = a sin (t) where a is the amplitude of motion and is the circular frequency of the motion. Then the motion is described by
es
.i n
where Fn is the natural frequency. From this, it is seen that if the stiffness increases, the natural frequency also increases, and if the mass increases, the natural frequency decreases. If the system has damping, which all physical systems do, its frequency of response is a little lower, and depends on the amount of damping.
Finite element vibrations
Any physical structure vibration can be modeled by springs (stiffnesses), masses, and dampers. In elementary models you use line springs and dampers, and point masses. In finite element models, the continuous nature of the stiffness and mass leads to the use of square matrices for stiffness, mass, and damping. They can still contain special cases of line element springs and dampers, as well as point masses. Dampers dissipate energy, but springs and masses do not. If you have a finite element system with many dof then the above single dof system generalizes to a displacement vector, X(t) interacting with a square mass matrix, M, stiffness matrix, K, damping matrix C, and externally applied force vector, F(t), but retains the same general form: M d2X / dt2 + C dX / dt + K X(t) = F(t)
Usually you are interested only in the first few natural frequencies. A zero natural frequency corresponds to a rigid body motion. If a shell model is used the rotational dof exist and the mass matrix is generalized to include the mass moments of inertia. For every natural frequency there is a corresponding vibration mode shape. Most mode shapes can generally be described as being an axial mode, torsional mode, bending mode, or general mode Like stress analysis models, probably the most challenging part of getting accurate finite element natural frequencies and mode shapes is to get the type and locations of the restraints correct. A crude mesh will give accurate frequency values, but not accurate stress values. TK Solver contains equations for most known analytic solutions for the frequencies of mechanical systems. They can be quite useful in validating the finite element frequency results.
There is a frequency, say k, and mode shape vector, Ak, for each degree of freedom, k. A matrix eigenvalue-eigenvector solution is much more computationally expensive that a matrix time history solution. Therefore most finite element systems usually solve for the first few natural frequencies. Depending on the available computer power, that may mean 10 to 100 frequencies. CosmosWorks includes natural frequency and mode shape calculations as well as time history solutions.
Page 2 of 2. Copyright J.E. Akin. All rights reserved.
.E
The SHM assumption generalizes to X(t) = A sin (t) where the amplitude, A, is usually called the mode shape vector at circular frequency . This leads to the general matrix eigenvalue problem
| K - 2 M | = 0.
M d2X / dt2 + K X(t) = 0.
plus the initial conditions on the displacement, X(0), and velocity, v(0) = dX / dt(0). Integrating these equations in time gives a time history solution. The solution concepts are basically the same, they just have to be done using matrix algebra. The corresponding SHM, or free vibration mode (C = 0, F = 0) for a finite element system is
es
.i n
Você também pode gostar
- Green's Function Estimates for Lattice Schrödinger Operators and Applications. (AM-158)No EverandGreen's Function Estimates for Lattice Schrödinger Operators and Applications. (AM-158)Ainda não há avaliações
- Seminar on Micro-Local Analysis. (AM-93), Volume 93No EverandSeminar on Micro-Local Analysis. (AM-93), Volume 93Ainda não há avaliações
- Lecture 4 NotesDocumento36 páginasLecture 4 Notesahmed11 engyemenAinda não há avaliações
- Vibration Analysis - Approximate Methods: Unit 4 - ContinuationDocumento29 páginasVibration Analysis - Approximate Methods: Unit 4 - ContinuationAdrian ArasuAinda não há avaliações
- Two Lecture VibrationDocumento12 páginasTwo Lecture VibrationUjjawal GuptaAinda não há avaliações
- 1 - Fundamentos Da Vibração MecânicaDocumento26 páginas1 - Fundamentos Da Vibração MecânicaWallace Franco da SilvaAinda não há avaliações
- Lecture 13Documento41 páginasLecture 13Mohamad AsrulAinda não há avaliações
- DOM M S D F Harmonical Excited Vibration 1Documento90 páginasDOM M S D F Harmonical Excited Vibration 1Prajapati DhavalAinda não há avaliações
- Notes Dynamics UC3MDocumento6 páginasNotes Dynamics UC3MAnonymous oFxrAqvAinda não há avaliações
- Dinamika StrukturDocumento25 páginasDinamika StrukturErik Wahyu PradanaAinda não há avaliações
- STRC201 Sdof JMWBDocumento99 páginasSTRC201 Sdof JMWBJura PateregaAinda não há avaliações
- 1 Single Degree of Freedom (SDOF) Systems: James MW Brownjohn, University of Plymouth, January 2005Documento99 páginas1 Single Degree of Freedom (SDOF) Systems: James MW Brownjohn, University of Plymouth, January 2005Amandeep SinghAinda não há avaliações
- STRC201 Sdof JMWB PDFDocumento99 páginasSTRC201 Sdof JMWB PDFAkash ChandraAinda não há avaliações
- JPD - 2M Vibrations NotesDocumento46 páginasJPD - 2M Vibrations NotesHillel BadermanAinda não há avaliações
- Submitted By:-Kumar AshishDocumento20 páginasSubmitted By:-Kumar AshishKumar AshishAinda não há avaliações
- Single Degree of Freedom SystemDocumento28 páginasSingle Degree of Freedom SystemAjeng Swariyanatar PutriAinda não há avaliações
- Vibration Reference.: Timoshenko MedalistDocumento15 páginasVibration Reference.: Timoshenko MedalistChandra ClarkAinda não há avaliações
- The' Wave Equation: 1.1 One Dimension: Waves On A Stretched StringDocumento12 páginasThe' Wave Equation: 1.1 One Dimension: Waves On A Stretched StringDavid ThomsonAinda não há avaliações
- NPTEL - Mechanical Engineering - Vibration ControlDocumento10 páginasNPTEL - Mechanical Engineering - Vibration Control8104772799Ainda não há avaliações
- Free Vibration of Single-Degree-Of-freedom SystemsDocumento7 páginasFree Vibration of Single-Degree-Of-freedom SystemsShafiq ShajaAinda não há avaliações
- Nuclear PhysicsDocumento11 páginasNuclear Physicsgiovanny_francisAinda não há avaliações
- ME312 Lab Manual 2021 - Cantilever BeamDocumento7 páginasME312 Lab Manual 2021 - Cantilever BeamPranav BajajAinda não há avaliações
- SHM NotesDocumento4 páginasSHM Notesgiulio.zizzo2850Ainda não há avaliações
- Physics Mid-Sem CompilationDocumento220 páginasPhysics Mid-Sem Compilationdhruv goraiAinda não há avaliações
- MECH226 Vibration Section 2. Forced Vibration of A Single Degree-Of-Freedom SystemDocumento9 páginasMECH226 Vibration Section 2. Forced Vibration of A Single Degree-Of-Freedom SystemkibzeamAinda não há avaliações
- Newtonian Mechanics - Part 1: L Del Debbio, University of EdinburghDocumento12 páginasNewtonian Mechanics - Part 1: L Del Debbio, University of Edinburghcharles luisAinda não há avaliações
- Harmonic Oscilator Lecture NotesDocumento5 páginasHarmonic Oscilator Lecture Notesdanger99Ainda não há avaliações
- Dynamics of A Mass-Spring-Pendulum System With Vastly Different FrequenciesDocumento6 páginasDynamics of A Mass-Spring-Pendulum System With Vastly Different FrequenciesvertugoAinda não há avaliações
- MCG4308 Lec4Documento25 páginasMCG4308 Lec4Christian PaultreAinda não há avaliações
- Bda31103 Lect02 - 1 Dof Part1Documento20 páginasBda31103 Lect02 - 1 Dof Part1Ong Kok MengAinda não há avaliações
- Lectures 23-24 Chapter 15 Fall 2009Documento28 páginasLectures 23-24 Chapter 15 Fall 2009tewari_skAinda não há avaliações
- Microsoft Powerpoint - 3-Introduction To Dynamic AnalysisDocumento37 páginasMicrosoft Powerpoint - 3-Introduction To Dynamic AnalysisyuchunieAinda não há avaliações
- Two-Degree-of-Freedom SystemsDocumento19 páginasTwo-Degree-of-Freedom SystemsMarwan NasserAinda não há avaliações
- Simple Harmonic Motion and Elastic EnergyDocumento5 páginasSimple Harmonic Motion and Elastic Energyalexduart01Ainda não há avaliações
- Applications of Fourier SeriesDocumento2 páginasApplications of Fourier SeriesMoiz Arif50% (2)
- Modal Analysis of Beams - An Experiment Symposium On Dynamic Problems of MechanicsDocumento9 páginasModal Analysis of Beams - An Experiment Symposium On Dynamic Problems of MechanicsnizamshahrinAinda não há avaliações
- A Summary of Basic Vibration Theory: Degree-Of-Freedom BlueDocumento22 páginasA Summary of Basic Vibration Theory: Degree-Of-Freedom BlueRui Pedro Chedas SampaioAinda não há avaliações
- Simple Harmonic Motion: Is SHM Sinusoidal Wave ?Documento5 páginasSimple Harmonic Motion: Is SHM Sinusoidal Wave ?ضياء بن احمد الكباريAinda não há avaliações
- Harmonically Excited VibrationsDocumento39 páginasHarmonically Excited VibrationsJuan Paulo MayorAinda não há avaliações
- Engineering Dynamics CourseworkDocumento14 páginasEngineering Dynamics CourseworkAli Abdulla100% (1)
- Simple Mass Spring SystemDocumento11 páginasSimple Mass Spring SystemArindam MondalAinda não há avaliações
- Loss of Energy Concentration in Nonlinear Evolution Beam Equations (Journal of Nonlinear Science) (2017)Documento39 páginasLoss of Energy Concentration in Nonlinear Evolution Beam Equations (Journal of Nonlinear Science) (2017)rxflexAinda não há avaliações
- Chapter 1 - Introduction To Mechanical Vibrations PDFDocumento13 páginasChapter 1 - Introduction To Mechanical Vibrations PDFLuchito CtAinda não há avaliações
- Wave Phenomena: Physics 15cDocumento29 páginasWave Phenomena: Physics 15cKattari DwiAinda não há avaliações
- Journal of Sound and Vibration 1997 - v200 31-40Documento10 páginasJournal of Sound and Vibration 1997 - v200 31-40Franco VillanuevaAinda não há avaliações
- Forced VibrationDocumento9 páginasForced Vibrationstphn_maturinAinda não há avaliações
- Notes On Mechanical Vibrations: 1 Masses and Springs-The Linear OscillatorDocumento10 páginasNotes On Mechanical Vibrations: 1 Masses and Springs-The Linear Oscillatoramlandas08Ainda não há avaliações
- Second-Order Linear Equations: 2.1 Classical MechanicsDocumento11 páginasSecond-Order Linear Equations: 2.1 Classical Mechanicssohail amarAinda não há avaliações
- Chapter1 PDFDocumento13 páginasChapter1 PDFnkoreisha7752Ainda não há avaliações
- Adv Lab OscillatorsDocumento12 páginasAdv Lab OscillatorsPeter John BolgertAinda não há avaliações
- Ch4 PDFDocumento31 páginasCh4 PDFRicardo ColosimoAinda não há avaliações
- Dynamic AnalysisDocumento16 páginasDynamic AnalysismshAinda não há avaliações
- Feynman Lectures Simplified 1B: Harmonic Oscillators, & ThermodynamicsNo EverandFeynman Lectures Simplified 1B: Harmonic Oscillators, & ThermodynamicsAinda não há avaliações
- Interactions between Electromagnetic Fields and Matter: Vieweg Tracts in Pure and Applied PhysicsNo EverandInteractions between Electromagnetic Fields and Matter: Vieweg Tracts in Pure and Applied PhysicsAinda não há avaliações
- Introduction to Non-Linear Mechanics. (AM-11), Volume 11No EverandIntroduction to Non-Linear Mechanics. (AM-11), Volume 11Ainda não há avaliações
- Ordinary Differential Equations and Stability Theory: An IntroductionNo EverandOrdinary Differential Equations and Stability Theory: An IntroductionAinda não há avaliações
- Mechanical Engineer SkillDocumento3 páginasMechanical Engineer Skillmesa142100% (1)
- Cad NotesDocumento61 páginasCad NotesNaga PrasadAinda não há avaliações
- Me6501 Computer Aided Design 2 Marks With AnswersDocumento12 páginasMe6501 Computer Aided Design 2 Marks With AnswersTrigger DineshAinda não há avaliações
- Two Marks Question and Answer Unit - I: Scad Engineering CollegeDocumento12 páginasTwo Marks Question and Answer Unit - I: Scad Engineering CollegeMohu CricketerAinda não há avaliações
- CadDocumento27 páginasCadTrigger DineshAinda não há avaliações
- Pneumatic SystemDocumento28 páginasPneumatic SystemMohd FazillAinda não há avaliações
- Mechanical Engineer ResumeDocumento1 páginaMechanical Engineer ResumeAala'a Khalil Abu AridaAinda não há avaliações
- Strength of Materials - 2marksDocumento37 páginasStrength of Materials - 2marksTrigger DineshAinda não há avaliações
- Heat Exchanger PDFDocumento9 páginasHeat Exchanger PDFsunita45Ainda não há avaliações
- QB M8Documento1 páginaQB M8vik03223Ainda não há avaliações
- 04 Eng Graphics 2002 PRTDocumento28 páginas04 Eng Graphics 2002 PRTRaghib ShakeelAinda não há avaliações
- Adv Midyear 2015Documento1 páginaAdv Midyear 2015Trigger DineshAinda não há avaliações
- Pavement DistressDocumento64 páginasPavement DistressTrigger DineshAinda não há avaliações
- Boiling and CondensationDocumento16 páginasBoiling and CondensationJunnaid NissarAinda não há avaliações
- Distress ManagementDocumento12 páginasDistress ManagementTrigger DineshAinda não há avaliações
- Analysis of Front Suspension Lower Control Arm of An Automobile Vehicle - Ijsrnet Editorial - AcademiaDocumento7 páginasAnalysis of Front Suspension Lower Control Arm of An Automobile Vehicle - Ijsrnet Editorial - AcademiaTrigger DineshAinda não há avaliações
- Introduction To Fluid Mechanics : Fred Stern, Tao Xing, Jun Shao, Surajeet GhoshDocumento44 páginasIntroduction To Fluid Mechanics : Fred Stern, Tao Xing, Jun Shao, Surajeet GhoshTrigger DineshAinda não há avaliações
- Condensation: The Lecture ContainsDocumento15 páginasCondensation: The Lecture ContainsTrigger DineshAinda não há avaliações
- Boiling and CondensationDocumento16 páginasBoiling and CondensationJunnaid NissarAinda não há avaliações
- Man and Environment: Asst. Dr. Nantana GajaseniDocumento50 páginasMan and Environment: Asst. Dr. Nantana GajaseniTrigger DineshAinda não há avaliações
- 8th Mech - BakDocumento19 páginas8th Mech - Bakbadboys123Ainda não há avaliações
- Tpde Rejinpaul - Com Question BankDocumento15 páginasTpde Rejinpaul - Com Question BankTrigger DineshAinda não há avaliações
- 303 Chapter1 2Documento9 páginas303 Chapter1 2Mohammed ImranAinda não há avaliações
- Response: Free or Forced in This Chapter: Free Response, I.E. No External Forces Are AppliedDocumento12 páginasResponse: Free or Forced in This Chapter: Free Response, I.E. No External Forces Are AppliedTrigger DineshAinda não há avaliações
- Electro Magnetic Pumping Braking System (11000)Documento1 páginaElectro Magnetic Pumping Braking System (11000)Trigger DineshAinda não há avaliações
- Response: Free or Forced in This Chapter: Free Response, I.E. No External Forces Are AppliedDocumento12 páginasResponse: Free or Forced in This Chapter: Free Response, I.E. No External Forces Are AppliedTrigger DineshAinda não há avaliações
- Ejsr 62 2 03Documento8 páginasEjsr 62 2 03Trigger DineshAinda não há avaliações
- Final Year Project Details (VPC)Documento1 páginaFinal Year Project Details (VPC)Trigger DineshAinda não há avaliações
- Regenerative BrakingDocumento2 páginasRegenerative BrakingTrigger DineshAinda não há avaliações
- Kern ComputingDocumento7 páginasKern ComputingTrigger DineshAinda não há avaliações
- Proportional Hydraulics Basic Level - Workbook - EN (TP 701) PDFDocumento144 páginasProportional Hydraulics Basic Level - Workbook - EN (TP 701) PDFLong Vu BuiAinda não há avaliações
- Form Inspeksi Mesin MillingDocumento17 páginasForm Inspeksi Mesin MillingSasa MonicaAinda não há avaliações
- Head LossDocumento1 páginaHead LossamrAinda não há avaliações
- Sans Titre PDFDocumento1 páginaSans Titre PDFjoker63000Ainda não há avaliações
- ISO 6358 ApplicabilityDocumento10 páginasISO 6358 ApplicabilityL095244Ainda não há avaliações
- Iso 13703-2000 PDFDocumento8 páginasIso 13703-2000 PDFs111_sunil0% (1)
- Design of Base Plate LKP Arm 4-F-30.01.2018Documento5 páginasDesign of Base Plate LKP Arm 4-F-30.01.2018HarikrishnaAinda não há avaliações
- SK200-8 YN11 Error CodesDocumento58 páginasSK200-8 YN11 Error Codest544207189% (37)
- Pew 209 .02Documento59 páginasPew 209 .02Raj BindasAinda não há avaliações
- Alliance Tires: Industrial Construction Machinary 321Documento1 páginaAlliance Tires: Industrial Construction Machinary 321José Rojas AlvaradoAinda não há avaliações
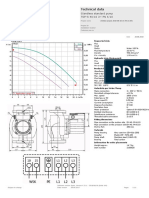
- FichaTécnicaMotor200KW PDFDocumento1 páginaFichaTécnicaMotor200KW PDFEdward Jr ChapetonAinda não há avaliações
- Astm A216Documento4 páginasAstm A216salazaralexi100% (1)
- BMS Cable MeasurmentDocumento2 páginasBMS Cable MeasurmentsamhardworkerAinda não há avaliações
- Manitowoc 4500 - 4665 - Parts ManualDocumento280 páginasManitowoc 4500 - 4665 - Parts ManualalbertoAinda não há avaliações
- Other Forms of Work and First Law of ThermodynamicsDocumento18 páginasOther Forms of Work and First Law of ThermodynamicsSerimAinda não há avaliações
- Conveyors and Conveying Systems (Lec1b)Documento81 páginasConveyors and Conveying Systems (Lec1b)Rhizhail100% (1)
- EXPERIMENTDocumento4 páginasEXPERIMENTBholenath BhaktAinda não há avaliações
- BOMBAS PRIMARIAS - Data - Sheet - TOP-S - 40 - 10 - 3 - PN - 6 - 10Documento1 páginaBOMBAS PRIMARIAS - Data - Sheet - TOP-S - 40 - 10 - 3 - PN - 6 - 10Sebastian FuentesAinda não há avaliações
- Service Manual #41Documento106 páginasService Manual #41GrindK0re73% (15)
- Royal Military College of Science - Cranfield University: ReliabilityDocumento4 páginasRoyal Military College of Science - Cranfield University: ReliabilitySanjay MehrishiAinda não há avaliações
- Cyclon 111Documento8 páginasCyclon 111mariobri_49809106650% (2)
- Design of Tension MembersDocumento11 páginasDesign of Tension MembersWilfharry billyAinda não há avaliações
- B.Tech UG Project Ideas 4Documento11 páginasB.Tech UG Project Ideas 4nambimunnaAinda não há avaliações
- Resonance and Analysis of Barton's Pendulum PDFDocumento17 páginasResonance and Analysis of Barton's Pendulum PDFmailbox_afeef2Ainda não há avaliações
- B62 0030 (Rev. E 2008.03) EN - THERMOPLASTIC, THERMOSETTING MATERIALS, THERMOPLASTIC ELASTOMERS AND RUBBERS - SPECIFICATIONSDocumento15 páginasB62 0030 (Rev. E 2008.03) EN - THERMOPLASTIC, THERMOSETTING MATERIALS, THERMOPLASTIC ELASTOMERS AND RUBBERS - SPECIFICATIONSDiego CamargoAinda não há avaliações
- HMC 080Documento12 páginasHMC 080Mohamed ElmakkyAinda não há avaliações
- Boiling and Condensation PDFDocumento11 páginasBoiling and Condensation PDFYeditha Satyanarayana MurthyAinda não há avaliações
- 9 Understanding Analysis Failures and WarningsDocumento6 páginas9 Understanding Analysis Failures and WarningsSara RamliAinda não há avaliações
- RHQ-IOCL-CPMSL-2020 Rev.0 Master Supplier ListDocumento224 páginasRHQ-IOCL-CPMSL-2020 Rev.0 Master Supplier ListKunal100% (1)
- Brilliant: Physics Olympiad Model ExaminationDocumento9 páginasBrilliant: Physics Olympiad Model ExaminationKalyani BaijuAinda não há avaliações