Table of Contents

Chapter 1 Author: Andrei Nistreanu ....................................................................................................3

Chapter 2 The tricks ............................................................................................................................3
Chapter 3 List of articles:.....................................................................................................................5
Chapter 4 Group theory.......................................................................................................................8
4.1 Basis ........................................................................................................................................8
4.2 Rotations................................................................................................................................11
4.3 Reflections.............................................................................................................................13
4.4 Group representations............................................................................................................20
4.5 Unitary Matrix ......................................................................................................................22
4.6 Schur's Lemma......................................................................................................................23
4.7 Great orthogonality theorem..................................................................................................23
4.8 Great orthogonality theorem (application)............................................................................24
4.9 D3 representations and irreducible representations...............................................................25
4.10 Basis Functions....................................................................................................................28
4.11 Projection Operators (D3)....................................................................................................29
4.12 Symmetry adapted linear combinations(C3v).....................................................................36
4.13 Bonding in polyatomics - constructing molecular orbitals from SALCs............................39
4.14 Product representations........................................................................................................40
4.15 Clebsch-Gordan coefficients for simply reducible groups (CGC)......................................42
4.16 Full matrix representations..................................................................................................49
4.17 Selections rules....................................................................................................................52
4.18 (SO3)Linear combinations of spherical harmonics of point groups....................................53
Chapter 5 Tensors...............................................................................................................................58
5.1 Direct products, vectors.........................................................................................................58
5.2 Tensor continuation Polarizability Directions cosines..........................................................66
Chapter 6 Fine structure.....................................................................................................................74
6.1 Angular Momentum...............................................................................................................74
6.2 Atom with Many Electrons....................................................................................................81
6.3 The band structure of blue and yellow diamonds..................................................................88
6.4 optical transition ...................................................................................................................90
6.5 angular momentum deduction...............................................................................................91
Chapter 7 Quantum mechanics and postulates...................................................................................99
7.1 The most important thing in Quantum Mechanics ...............................................................99
7.2 Matrix representation of operators:.......................................................................................99
7.3 Hermitian Operators..............................................................................................................99
Chapter 8 Clebsch-Gordan...............................................................................................................100
8.1 Addition of angular Momenta: Clebsch-Gordan coefficients I..........................................100
8.2 Clebsch-Gordan coefficients (other source)II.....................................................................102
8.3 Examples..............................................................................................................................105
Chapter 9 Binomial relationship.......................................................................................................108
9.1 Permutations........................................................................................................................108
9.2 Combinations......................................................................................................................109
9.3 Binomial formula ...............................................................................................................109
9.4 A relationship among binomial coefficents (Wigner [55] pag 194).....................................111
1
Chapter 10 Explicit formulas for GC or Wigner coefficients...........................................................112
10.1 Equivalence between Fock states or coherent states and spinors......................................112
10.2 Functions of operators ......................................................................................................113
10.3 Generating Function of the States .....................................................................................114
10.4 Evaluation of the Elements of the Wigner Rotation Matrix..............................................115
10.5 RWF lecture.......................................................................................................................117
10.5.1The Beta Function..........................................................................................................117
10.6 Explicit expression for Wigner (CG) coefficients I...........................................................119
10.7 Explicit expression for Clebsch-Gordan coefficients (CGC) (Wigner's formula)II..........121
10.8 Explicit expression for Clebsch-Gordan coefficients (CGC) (Wigner's formula)III ........125
10.9 Van der Waerden symmetric form of CGC .......................................................................127
10.10 Wigner 3j symbols or Racah formula .............................................................................131
Chapter 11 The formula of Lagrange and Sylvester for function F of matrix .................................134
11.1 Sylvester formula for Rabi oscillations full deduction......................................................134
11.2 Eigenvalues and Eigenvectors...........................................................................................135
11.3 Properties of determinants.................................................................................................136
11.4 The Method of Cofactors...................................................................................................138
11.5 Cramer's rule proof............................................................................................................138
11.6 Vandermonde determinant ................................................................................................140
11.7 Vandermonde determinant and Cramer's rule result Lagrange's interpolation formula.. . .141
11.8 Cayley-Hamilton Theorem................................................................................................145
11.8.1 The Theorem.................................................................................................................145
11.8.2The Simple But Invalid Proof........................................................................................146
11.8.3An Analytic Proof..........................................................................................................146
11.8.4Proof for Commutative Rings........................................................................................148
11.8.5Appendix A. Every Complex Matrix is Similar to an Upper Triangular Matrix...........148
11.8.6APPENDIX B. A Complex Polynomial Is Identically Zero Only If All Coefficients Are
Zero..........................................................................................................................................149
11.8.7From Wikipedia, the free encyclopedia.........................................................................149
11.9 SYLVESTER'S MATRIX THEOREM..............................................................................150
11.10 Final formula....................................................................................................................153
Chapter 12 Time evolution two level atom Rabi frequency.............................................................154
12.1 Two level atom..................................................................................................................154
2
Chapter 1 Author: Andrei Nistreanu
I must put the heading 4 because the numbering of formulas become long 10.10.12
Lenef
Chapter 2 The tricks
At each bibliography name you must to create a button back so at the page insert the text : Insert
Bookmark give a number
JsMath rfs10 hhand lhand H L
ctrl +b J
ctrl sift+b J
2

ctrl shift +p J
2
Vezi flv-urile
alignl pentru ecuatii
dupa ce apesi hyperlinkul nu face ctrl-z ci Edit si vezi undo sau redo New Paragraph
fn apesi F3 si apare
E=mc
2
(2.1)
Wikipedia in order to remove hyper-links: select all right click remove hyper-link
Images , jpg from internet : click on the images after double click on the graphics from: Format
styles and formatting

ghilimelee ca text (b'
+

) and(b'

)
Pui caption la figuri apoi click dreapta wrap(a inveli, infasura) > optimal to page
spelling and grammar intri in tools in options languages settings si pui ca sa faca spell check
3( x+4)2( x1)=3 x+12(2 x2)
=3 x+122 x+2
=x+14
"" =alignl
3
x+y = 2
x = 2y
http://wiki.services.openoffice.org/wiki/Documentation/OOoAuthors_User_Manual/Writer_Guide/Cre
ating_a_table_of_contents
1. Mai intai configurezi headingsurile: If you want numbering by chapter, you first have to
configure chapter numbering for the document. Your document uses no heading styles and is
not configured to number the headings. Such numbering can be configured under Tools >
Outline Numbering; normally you would use the "Heading 1" style for the top-level heading.
2. Deci pentru chapter pui hedings 2 show sublevels 1
3. pentru paragrafe pui headings 3 - show sublevels 2 (inserezi si din coltul stanga de sus pui
hedings 3)
4. la equatii pui levelul 2 sau 3 daca pui level 2 atunci apare apare 2 cifre numarul capitolului
punct numarul ecuatiei; daca pui level 3 apare 3 numere adica este inclus si num paragrafului
5. Contents of table : Insert > Indexes and tables
6. right click on the field of the tables: Edit index/tables
7. if you want hyper-link on the headings 3 then chose level 3, after chose hyperlink to pe click on
the page or on the entry
windows Ooo 3.2.1 cu negru vede default faci dublu click pe ecuatie si schimbi la fiecare in parte
dac vrei din gray in negru sau scrie in windows
Right-click page este page setup margins
Open the Navigator (press F5).
1. Click the + sign next to Indexes.
2. Right-click on the desired index and choose Index > Edit.
3. Delete table of contents
In order to change the cross-reference in a Hyperlink:
-make a cross reference
-Insert that cross-reference > Hyperlink
-Click the target in document button to the right of the Target text field, simply
type the name into the target text field box.
-Click apply
Mai bine ctrl-B ctrl U si blue caci in pdf tot nu se vede displayed information
Dar may bine hyperlink caci mai apoi cu navigatorul te intorci ina poi F5 si alegi hyperlinkul
dar daca ai o mie de hyperlincuri?
Add special character in Math first see the name in Latex e.g. \dagger or \otimes after go in insert
object formula or F2 and chose catalog special edit symbols
Step 4. Add the symbol.
(a) In the Edit symbols dialog, delete the entry under Old symbol
(b) In the symbol field, type the command that you want to use to refer to the symbol. For example, say
you want to use the binary order symbol . If you type succ then you will be able to access the
4
symbol using %succ in the equation editor.
(c) Select the font that you want to use under the font dropdown menu. The MIT math fonts are named
Math1 through Math5. You will need to browse through the catalog to find your symbol.
(d) Select the symbol that you want to add and click add.

ubuntu 3.2.1 cu gray dublu click si schimbi in gray
p
j
=

i

c
a
c
(ci )(c j ) E
i
p
j
=

i

c
a
c
(ci )(c j ) E
i
p
j
=

i

c
a
c
(ci )(c j ) E
i
p
j
=

i

c
a
c
(ci )(c j ) E
i
p
j
=

i

c
a
c
(ci )(c j ) E
i
p
j
=

i

c
a
c
(ci )(c j ) E
i
latex
http://es.wikipedia.org/wiki/LaTeX
0=a_{11} + a_{12}
0=a
11
+a
12
correct
x^{a+b}=x^ax^b x
a+b
=x
a
x
b
spatiu intre a si x
x'+x'' = \dot x + \ddot x x ' +x ' ' = x+

x nu se pune \
E &=& mc^2
E = mc
2
&=~
You can do it with LaTeX using Eqe:
\definecolor{grey}{rgb}{0.5,0.5,0.5}
\textcolor{grey}{What you want in grey}
or for example:
\definecolor{grey}{rgb}{0.5,0.5,0.5}
\textcolor{grey}{$\left(\begin {array}{c}7289\\2\end {array}\right) = 65\times10^9$}
Chapter 3 List of articles:
[1] A. Lenef, S. Rand , Electronic structure of the N-V center in diamond: Theory, Phys. Rev. B 53
13441(1996)(Ref. Pag:34, 44, 48)
[2] N. Manson, R. McMurtrie , Issues concerning the nitrogen-vacancy center in diamond, J.
Lumin. 127, 98 103(2007)
[3] J. Loubser and J. Van Wyk Electron spin resonance in the study of diamond, Rep. Prog. Phys.
41 1201-48(1978)
[4] M. Doherty, N. Manson, P. Delaney and L. Hollenberg , The negatively charged N-V center in
diamond: the electronic solution, arXiv:1008.5224(2010)
[5] J. Maze, A. Gali, E. Togan, Y Chu, A. Trifonov, E. Kaxiras, And M. Lukin , Propreties of
nitrogen-vacancy centers in diamond: the group theoretical approach, New J. Phys. 13
025025(2011)
[6] Jacobs P. , Group theory with applications in Chemical Physics, (Cambridge 2005)(Ref.
Pag:13,13)
[7] B. Naydenov, F. Dolde, L. Hall, C. Shin, H Fedder, L. Hollenberg, F. Jelezco, and J. Wrachtrup,
5
Dynamical decoupling of a single-electron spin at room temperature, Phys. Rev. B 83,
081201(R)(2011)
[8] A. Nizovtsev, S. Kilin, V. Pushkarchuk, A. Pushkarchuk, and S. Kuten , Quantum informatics.
Quantum information processors, Optics and Spectroscopy 108,2 230(2010)
[9] A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Vol. I
(Moscow 1972, Oxford 1970)
[10] A. Lesk, Introduction to Symmetry and Group Theory for Chemists, Dordrecht (2004)
[11] C. Vallance, Lecture, Molecular Symmetry, Group Theory & Applications (2006)(Ref.
Pag:34,36)
[12] R. Powell,_Symmetry, Group Theory, and the Physical Properties of Crystals Springer (2010)
[13] M. Dresselhaus, Application of Group Theory to the Physics of Solids, Spring 2002
[14] , Curs de matematica superioara, Chisinau 1971
[15] H. Eyring and G. Kimball, Quantum Chemistry, Singapore, New-York, London (1944)
[16] K. Riley, M. Hobson, Mathematical Methods for Physics and Engineering: A Comprehensive
Guide, Second Edition, Cambridge 2002
[17] D. Long, The Raman Effect A Unified Treatment of the Theory of Raman Scattering by
Molecules , (2002)
[18] L. Barron, Molecular Light Scattering and Optical Activity(2004) (Ref. Pag:134, 134)
[19] Eric C. Le Ru, Pablo G. Etchegoin, Principles of Surface Enhanced Raman Spectroscopy,
(2009)(bond- polarizability model Wolkenstein)
[20] D. Griffiths, Introduction to electrodynamics, New Jersey (1999)
[21] M. , , Leningrad 1960
[22] . . . . , . . 1 2, . .: 1949
[23] H. Heinbockel, Introduction to tensor calculus,(1996)
[24] G. Arfken, H. Weber, Mathematical Methods For Physicists, International Student
Edition(2005)
[25] B. Berne and R. Pecora, Dynamic Light Scattering, New York 1990
[26] Liang, ScandaloJ. Chem. Phys. 125, 194524 (2006)
[27] R. Feynman, The Feynman Lectures on Physics, V I,II, III, California (1964)
[28] C.J. Foot, Atomic Physics , Oxford 2005(Ref. Pag:57)
[29] C. Gerry, Introductory Quantum Optics, Cambridge 2005
[30] E. Kartheuser , Elements de MECANIQUE QUANTIQUE , Liege 1998?!
[31] M. Kuno, Quantum mechanics, Notre Dame, USA 2008(Ref. Pag:32)
[32] M. Kuno, Quantum spectroscopy, Notre Dame,USA 2006
[33] I. Savelyev, Fundamental of theoretical Physics,Moscow 1982
[34] I. Savelyev, Physics: A general course vol. I,III,III, Moscow 1980
[35] .. . [ 5, 1]
[36] . . , M 1991
[37] S. Blundell, Magnetism in condensed matter,Oxford 2001
[38] P. Atkins, Physical Chemistry
[39] J. Sakurai, Modern quantum mechanics, 1993
[40] A. Matveev , , Moscow 1989(Ref. Pag:32)
[41] . , , 2001
[42] A. Messiah, Quantum mechanics
[43] G. Arfken, H. Weber, Mathematical Methods For Physicists, International Student
Edition(2005)
[44] C. Clark , Angular Momentum, 2006 august (5 pag)
6
[45] A. Restrepo, Group theory in Quantum Mhechanics, (gt3)(2009)
[46] . , , 1976
[47] http://en.wikipedia.org/wiki/Lowering_operator
[48] W. Nolting, Quantum thory of magnetism, Springer-Verlag Berlin Heidelberg 2009
[49] I. Irodov, Problems in General Physics, English translation, Mir Publishers, 1981 Moscow
[50] Abhay Kumar Singh, Solutions to Irodov's Problems in General Physics Vol. I and 2, New
Delhi (2005)
[51] G. Herzberg, Atomic Spectra and Atomic Structure, New-York (1944)
[52] M. Mueller, Fundamentals of Quantum Chemistry, New-York (2002)
[53] E. U. Condon, G. H. Shortley, The Theory of Atomic Spectra Cambridge (1959)
[54] D. Perkins, Introduction to High Energy Physics, Cambridge (2000)
[55] E. Wigner, Group Theory And Its Application To The Quantum Mechanics Of Atomic
Spectra, New-York (1959) (Ref. Pag: 117)
[56] K. Schulten, Notes on Quantum Mechanics, Universities of Illinois (2000)
[57] M Caola, Lat. Am. J. Phys. Educ. Vol. 4, No. 1, Jan 2010 p84 (Ref. Pag: )
[58] Calais J-L., I. Jour. Of Quant. Chem. Vol.II, 715-727(1968)(Ref. Pag: )
[59] L. C. Biedenharn, J.D. Louck, Angular momentum in quantum physics, London (1981) (Ref.
Pag: 125, 130)
[60] E.B. Manoukian, Quantum Theory:A Wide Spectrum , Springer (2006)(Ref. Pag: 117 )
[61] Smirnov V., Cours de Mathmatique Suprieure , tome III deuxime partie dition MIR
Moscou 1972
[62] Robuk V. , Nuc. Ins. and Meth. in Phys. Res. A 534, p 319-323 (2004)
[63] Claude F., Atomes et lumire :Interactions Matire rayonnement, Universit Pierre et Marie
Curie (2006)
[64] Orszag M., Quantum Optics, Springer 2008
[65] Scully M., Zubairy M., Quantum optics, Cambridge 2001
[66] Brink Satchler Angular_momentum(1968)
[67] Rieger P., Electron Spin Resonance: Analysis_and_Interpretation, Royal Society of Chemistry
(2007)
[68] Jones H. Groups, Representations, and Physics (IPP, 1998) (Ref. Pag: 23)
[69] Weissbluth M., Atoms and molecules, Academic Press Inc.,U.S.(1978)(Ref. Pag:13, 25, 32, 35,
40, 57, 55)
[70] Ludwig W., Falter C., Symmetries in Physics: Group Theory Applied to Physical Problems,
Springer Series In Solid-State Sciences 64(1988)(Ref. Pag:14, 42, 46, 48, 53, 55)
[71] Inui T., Tanabe I.,Onodera I.,Group Theory and its Applications in Physics,Springer Series In
Solid-State Sciences 78(1990)(Ref. Pag:12, 34, 52, 53)
[72] Harris D., Symmetry and Spectroscopy: An Introduction to Vibrational and Electronic
Spectroscopy, Dover (1989)(Ref. Pag:32)
[73] Tinkham M., Group Theory and Quantum Mechanics, Dover(1992) (Ref. Pag:32, 132, 134)
[74] Cornwell J., Group Theory in Physics, Volume 1 (Techniques of Physics) , Academic Press
London (1984) (Ref. Pag:43)
[75] Cornwell J., :Symmetry Proprieties of the Clebsch-Gordan Coefficients, phys. stat. sol.(b)
37,225(1970) (Ref. Pag:42, 44)
[76] VAN DEN Broek P.,Cornwell J., :Clebsch-Gordan Coefficients of Symmetry Groups, phys.
stat. sol. (b) 90,211(1978) (Ref. Pag:44)
[77] Sugano S., Tanabe Y., Kamimura H., Multiplets of Transition-Metal Ions in Crystals,
Academic Press ,New-York 1970 (Ref. Pag:49, 48)
7
[78] Cornwell J., Group theory in physics ,Academic Press London (1997) (Ref. Pag:51)
[79] Fitts D.D., Principles of Quantum Mechanics, as Applied to Chemistry and Chemical Physics,
Cambridge (2002)(Ref. Pag:57 )
[80] Racah G., (I) Phys. Rev. 61, 186197 (1942) (Ref. Pag:128 )
[81] Racah G., (II)Phys. Rev. 62, 438462 (1942) (Ref. Pag:128 )
[82] Judd B., Operator Techniques in Atomic Spectroscopy, Princeton University Press(1998)(Ref.
Pag:128 )
[83] Griffith J., The Theory of Transition-Metal Ions Cambridge (1971)(Ref. Pag:127 )
[84] Edmonds A., Angular momentum in quantum mechanics. [Rev. printing, 1968]Princeton
(1957) (Ref. Pag:127)
[85] Sobelman I., Atomic Spectra and Radiative Transitions(1992) (Ref. Pag:133)
Wolkenstein, M. I94I C.R. Acad. Sci., U.R.S.S. 32, 185.
Eliashevich, M. & Wolkenstein, M. I945 J. Phys., Moscow, 9, 101, 326
Chapter 4 Group theory
4.1 Basis
pag 11 [10]
Definition of a group
A group consists of a set (of symmetry operations, numbers, etc.) together with a rule by which any two
elements of the set may be combined which will be called, generically, multiplication with the
following four properties:
1 Closure: The result of combining any two elements the product of any two elements is another
element in the set.
2 Group multiplication satisfies the associative law: a (b c) = (a b) c for all elements a, b and c of
the group.
3 There exists a unit element, or identity, denoted E, such that E a = a for any element of the group.
4 For every element a of the group, the group contains another element called the inverse, a1, such
that a a1 = E. Note that as EE = E, the inverse of E is E itself.
Examples of groups
Elements of the group Rule of combination
1. covering operations of an object Successive application
2. All real numbers Addition
3. All complex numbers Addition
4. All real numbers except 0 Multiplication
5. All complex numbers except (0, 0) Multiplication
6. All integers Addition
8
7. Even integers Addition
8. The n complex numbers of the form cos 2k/n + i sin 2k/n, k = 0, . . . , n 1 Multiplication
9. All permutations of an ordered set of objects Successive application
A permutation is a specification of a way to reorder a set. For example, the group of permutations of
two objects contains two elements: the identity, first first, second second and the exchange, first
second, second first. This group is isomorphic to the group formed by 1 and 1 under
multiplication.
10. All possible rotations in three-dimensional space Successive application
Pag 15 [10]
Def. A point group is the symmetry group of an object of finite extent, such as an atom or molecule.
Pag 3. [11]
A symmetry operation is an action that leaves an object looking the same after it has been carried out.
For example, if we take a molecule of water and rotate it by 180 about an axis passing through the
central O atom (between the two H atoms) it will look the same as before. It will also look the same if
we reflect it through either of two mirror planes, as shown in the figure below.
1. E - the identity. The identity operation consists of doing nothing, and the corresponding symmetry
element is the entire molecule. Every molecule has at least this element.
2. C
n
- an n-fold axis of rotation. Rotation by 360/n leaves the molecule unchanged. The H2O
molecule above has a C
2
axis. Some molecules have more than one C
n
axis, in which case the one with
the highest value of n is called the principal axis. Note that by convention rotations are counter-
clockwise about the axis.
3. - a plane of symmetry. Reflection in the plane leaves the molecule looking the same. In a molecule
that also has an axis of symmetry, a mirror plane that includes the axis is called a vertical mirror plane
and is labelled
v
, while one perpendicular to the axis is called a horizontal mirror plane and is labelled

h
. A vertical mirror plane that bisects the angle between two C
2
axes is called a dihedral mirror plane,

d
.
4. i - a centre of symmetry. Inversion through the centre of symmetry leaves the molecule unchanged.
Inversion consists of passing each point through the centre of inversion and out to the same distance on
the other side of the molecule. An example of a molecule with a centre of inversion is shown below.
5. S
n
- an n-fold improper rotation axis (also called a rotary-reflection axis). The rotary reflection
9
operation consists of rotating through an angle 360/n about the axis, followed by reflecting in a plane
perpendicular to the axis. Note that S
1
is the same as reflection and S
2
is the same as inversion. The
molecule shown above has two S
2
axes.
C
nv
contains the identity, an n-fold axis of rotation, and n vertical mirror planes
v
.
C
nh
- contains the identity, an n-fold axis of rotation, and a horizontal reflection plane
h
(note that in
C
2h
this combination of symmetry elements automatically implies a centre of inversion).
D
n
- contains the identity, an n-fold axis of rotation, and n 2-fold rotations about axes perpendicular to
the principal axis.
D
nh
- contains the same symmetry elements as D
n
with the addition of a horizontal mirror plane.
Now we will investigate what happens when we apply two symmetry operations in sequence. As an
example, consider the NH
3
molecule, which belongs to the C
3v
point group. Consider what happens if
we apply a C
3
rotation followed by a
v
reflection. We write this combined operation
v
C
3
(when
written, symmetry operations operate on the thing directly to their right, just as operators do in quantum
mechanics we therefore have to work backwards from right to left from the notation to get the correct
order in which the operators are applied).
The combined operation
v
C
3
is equivalent to
v
'', which is also a symmetry operation of the C
3v
point
group. Now lets see what happens if we apply the operators in the reverse order i.e. C
3

v
(
v
followed
by C
3
).
10
There are two important points that are illustrated by this example:
1. The order in which two operations are applied is important. For two symmetry operations A and B,
AB is not necessarily the same as BA, i.e. symmetry operations do not in general commute. In some
groups the symmetry elements do commute; such groups are said to be Abelian.
2. If two operations from the same point group are applied in sequence, the result will be equivalent to
another operation from the point group. Symmetry operations that are related to each other by other
symmetry operations of the group are said to belong to the same class. In NH
3
, the three mirror planes

v
,
v
' and
v
'' belong to the same class (related to each other through a C
3
rotation), as do the rotations
C
3
+
and C
3
-
(anticlockwise and clockwise rotations about the principal axis, related to each other by a
vertical mirror plane).
or
Pag 26 [12]
Group multiplication Table
E A B C D F
E E A B C D F
A A E D F B C
B B F E D C A
C C D F E A B
D D C A B F E
F F B C A E D
Consider a group consisting of six elements represented by the letters A , B , C , D , E , and F that
obey the multiplication table shown above. The elements in the table are the product of the element
designating its column and the element designating its row. Following this convention, the table shows
that the identity element is a member of the group, the product of any two elements is an element of the
group, and each group element has an element in the group that is its inverse. Each element appears
only once in any given row or column. The associative law holds but the commutative law does not
hold for all products so the group is not Abelian. The order of the group is 6.
4.2 Rotations
11
pag 22 [14]
Rotation of Cartesian axes by an angle o about the
z-axis.
j=j' , =' +o
x=jcos, y=jsin
x ' =jcos' , y' =jsin '
x=jcos(' +coso)=j(cos' cososin ' sino)=x ' cosoy ' sin o
y=jsin (' +cos o)=j(sin ' coso+cos' sin o)=y' coso+x' sino
finally we get
x=x' cosoy' sino
y=x ' sin o+y ' cos o
z=z '
(4.2.1)
Another method (pag 780 [16] )that you can sum the
projections (the triangle rule x ' =x+y ) so we have
that:
x ' =x coso+ysino
see Fig 1
and the same for the other
y' =xsin o+ycos o
the transformation matrix are:
R=
(
coso sin o 0
sino coso 0
0 0 1
)
(4.2.2)
and from (4.2.1) we have the inverse:
R
1
=
(
coso sin o 0
sino coso 0
0 0 1
)
13
(4.2.3)
Thus we can write 321 in matrix form
r=R
1
r '
r ( x , y , z)
28
r ' =Rr see pag 51[71]
(4.2.4)
12
Fig 1
y
x
o
x coso
y sino
x '
pag 2 [13] also see [69] pag 61-63:
Figure 1.1: The symmetry operations on an equilateral triangle,
are the rotations by !2n/ 3 about the origin 0 and the rotations
by n about the axes 01, 02, and 03.
As a simple example of a group, consider the permutation group
for three elements, P(3). Below are listed the 3!=6 possible
permutations that can be carried out; the top row denotes the initial
arrangement of the three numbers and the bottom row denotes the
final arrangement.
This is for group D3:
E=
(
1 2 3
1 2 3
)
A=
(
1 2 3
2 1 3
)

B=
(
1 2 3
1 3 2
)
C=
(
1 2 3
3 2 1
)
D=
(
1 2 3
3 1 2
)
F=
(
1 2 3
2 3 1
)
(AB)C = DC = B
A(BC) = AD = B
bellow 14:
E=
(
1 0
0 1
)
A=
(
1 0
0 1
)

B=
(
1/ 2 .3/ 2
.3/ 2 1/ 2
)
C=
(
1/ 2 .3/ 2
.3/ 2 1/ 2
)
D=
(
1/ 2 .3/ 2
.3/ 2 1/ 2
)
F=
(
1/ 2 .3/ 2
.3/ 2 1/ 2
)
For C
3v
:
we have see[6] pag 70-71:
C
3v
={ E C
3
+
C
3

c
d
c
e
c
f
}
we have two rotations using for C
3
+

o=
2n
3
and for C
3

o=
2n
3
in eq.(4.2.3):
C
3
+
=
(
1/ 2 .3/ 2
.3/ 2 1/ 2
)
and
C
3

=
(
1/ 2 .3/ 2
.3/ 2 1/ 2
)
4.3 Reflections
at page 59 [6] for reflection in plane we have:
from theFig. 2 we put
](P'O c )=x
](YOP')=y we have we need to find the angle:
13
Fig. 2 Reflection of a point P(x y) in a mirror
plane whose normal m makes an angle with
y,so that the angle between and the zx plane is
0 . OP makes an angle o with x . P'(x'
y') is the reflection of P in x=0o , and OP'
makes an angle 20o with x .
x+x+o=2x+o (4.3.1)
We make the system of eq.:

2x+y+o=n/ 2
x+y+0=n/ 2
(4.3.2)
The solution is
x=0o (4.3.3)
Substitution of (4.3.3)in(4.3.1) yields
20o (4.3.4)
x=cos o and y=sin o
x ' =cos(20o)=x cos(20)+ysin(20) and
y' =sin( 20o)=xsin(20)ycos(20)
thus we got the transformation:
|
x '
y'
z'

=
|
cos(20) sin( 20) 0
sin(20) cos( 20) 0
0 0 1
|
x
y
z

(4.3.5)
With the representation :
I(c(0 y))=
|
cos(20) sin(20) 0
sin (20) cos(20) 0
0 0 1

(4.3.6)
Thus we have three reflections:
for
c
d
0=0 ,for
c
e
0=
n
3
and for
c
f
0=
n
3
in eq.(4.3.6):
c
d
=
(
1 0
0 1
)
c
e
=
(
1/ 2 .3/ 2
.3/ 2 1/ 2
)
c
f
=
(
1/ 2 .3/ 2
.3/ 2 1/ 2
)
for representation of
S
3
we have
e=
(
1 0
0 1
)
a=
(
1/ 2 .3/ 2
.3/ 2 1/ 2
)
b=
(
1/ 2 .3/ 2
.3/ 2 1/ 2
)
c=
(
1 0
0 1
)
d=
(
1/ 2 .3/ 2
.3/ 2 1/ 2
)
f =
(
1/ 2 .3/ 2
.3/ 2 1/ 2
)
d=D, f=F, c=A, a=B where the signs in principal diagonal is ganged, and b=C where the signs in
principal diagonal is ganged see 13 above.
In conclusion we see that
D
3
C
3v
also with
S
3
:see [70]pag 409 .
14
pag 27 [10]
Linear transformations and matrices
in linear transformation the most important class of geometrical manipulations is the set of linear
transformations, for which the effect on a point is given by the linear equations:
x
f
=a
11
x
i
+a
12
y
i
+a
13
z
i
y
f
=a
21
x
i
+a
22
y
i
+a
23
z
i
z
f
=a
31
x
i
+a
32
y
i
+a
33
z
i
in which (x
i
, y
i
, z
i
) and (x
f
, y
f
, z
f
) are vectors representing the initial and final points, and the a
ij
are real
numbers characterizing the transformation. All the covering operations we have dealt with are of this
type.
Matrix notation is a shorthand way of writing such systems of linear equations, that avoids tedious
copying of the symbols x
i
, y
i
and z
i
. The application of the identity matrix:
(
x
f
y
f
z
f
)
=
(
1 0 0
0 1 0
0 0 1
)
(
x
i
y
i
z
i
)
in abbreviations of system equations:
x
f
=1x
i
+0y
i
+0z
i
y
f
=0x
i
+1y
i
+0z
i
z
f
=0x
i
+0y
i
+1z
i
in general the array of numbers:
(
a
11
a
12
a
13
a
21
a
22
a
23
a
31
a
32
a
33
)
is called a matrix. The numbers
a
ij
are its elements: the first subscript specifies the row and the
second subscript specifies the column.
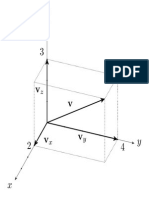
Each of the symmetry operations we have defined geometrically can be represented by a matrix. The
elements of the matrices depend on the choice of coordinate system.
15
The operations
c
v
, the mirror reflection in the y-z plane, has the effect in this coordinate system of
reversing the sign of the x-coordinate of any point it operates on. This effect is specified by the
equations:

x
f
=x
i
, y
f
=y
i
, z
f
=z
i
or bu the matrix equation:
(
x
f
y
f
z
f
)
=
(
1 0 0
0 1 0
0 0 1
)
(
x
i
y
i
z
i
)
The identity operation is expressed by identity matrix:
I =
(
1 0 0
0 1 0
0 0 1
)
Successive transformations; matrix multiplication
Because the successive application of two linear transformations is itself a linear transformation, it
must also correspond to a matrix. The matrix corresponding to a compound transformation can be
computed directly from the matrices corresponding to the individual transformations. Let us derive the
formulas; for simplicity we shall work in two dimensions. Given two linear transformations:
x
f
=a
11
x
i
+a
12
y
i
y
f
=a
21
x
i
+a
22
y
i
and
x'
f
=b
11
x'
i
+b
12
y'
i
y'
f
=b
21
x '
i
+b
22
y'
i
use the final point of the first transformation as the initial point of the second. That is, let
x '
i
=x
f
=a
11
x
i
+a
12
y
i
y'
i
=y
f
=a
21
x
i
+a
22
y
i
then
x'
f
=b
11
( a
11
x
i
+a
12
y
i
)+b
12
( a
21
x
i
+a
22
y
i
)
y'
f
=b
21
(a
11
x
i
+a
12
y
i
)+b
22
(a
21
x
i
+a
22
y
i
)
or
x '
f
=(b
11
a
11
x
i
+b
12
a
21
) x
i
+(b
11
a
12
+b
12
a
21
) y
i
y'
f
=(b
21
a
11
x
i
+b
22
a
21
) x
i
+( b
21
a
12
+b
22
a
22
) y
i
The last set of equations is in the standard form for a linear transformation. Its matrix form is:
(
x '
f
y'
f
)
=
(
(b
11
a
11
x
i
+b
12
a
21
) (b
11
a
12
+b
12
a
21
)
(b
21
a
11
x
i
+b
22
a
21
) (b
21
a
12
+b
22
a
22
)
)(
x
i
y
i
)
16
In more than two dimensions, the calculation is similar. The general result is that: if the matrix
C=
(
c
11
... c
1n
... ... ...
c
n1
... c
nn
)
A=
(
a
11
... a
1n
... ... ...
a
n1
... a
nn
)
B=
(
b
11
... b
1n
... ... ...
b
n1
... b
nn
)
we say that C is the product of B and A: C=BA . The elements of C are given by the formula:
c
ik
=

j =1
n
b
ij
a
jk
If the rows of B and the columns of A are considered as vectors, then the element
c
ik
is the dot
product of the i th row of B with the k th column of A:
C=
(

... c
ik
... ...

)
=
(
b
i1
b
i2
... b
i n
)

(
a
1k
a
2k
...
a
nk
)
The effect on a matrix of a change in coordinate system
The elements of the matrix that corresponds to a geometrical operation such as a rotation depend on the
coordinate system in which it is expressed. Consider a mirror reflection, in two dimensions, expressed
in three different coordinate systems, as shown in Figure 52. The mirror itself is in each case vertical,
independent of the orientation of the coordinate system.
17
Figure 5.2. Expression of a reflection in a mirror plane in three different coordinate systems. Note that
the points
x
i
, y
i
and
x
f
, y
f
dont change position. Only the coordinate axes change.
The relationships between the matrices representing the reflection in different coordinate systems are
expressible in terms of the matrix S that defines the relationships between the coordinate systems
themselves. Suppose ( x , y) and ( x' , y' ) are two pairs of normalized vectors oriented along the
axes of two Cartesian coordinate systems related by a linear transformation:
(
x '
y'
)
=S
(
x
y
)
If the matrix A represents the mirror reflection in the ( x , y) coordinate system, then the matrix that
represents the reflection in the ( x' , y' ) coordinate system is the triple matrix product S
1
AS ,
where S
1
is the inverse of S. Such a change in representation induced by a change in coordinate
system is called a similarity transformation.
Traces and determinants
Linear transformations that correspond to nonorthogonal matrices distort lengths or angles. The trace
and determinant of a matrix provide partial measures of the distortions introduced. The trace of a
matrix is defined as the sum of the diagonal elements.
Tr A=

i =1
n
a
ii
det
(
a b
c d
)
=adbc
Analogous but more complicated formulas define the determinants of square matrices of higher
dimensions. (A square matrix is a matrix which has the same number of rows as columns.) It is not
possible to define the determinant of a non-square matrix.
18
What conclusions do these examples suggest? First, note that only the first six examples are orthogonal
transformations. The determinant of each of these matrices is +1 or 1. Every matrix that represents an
orthogonal transformation must have determinant 1.
19
The importance of the trace and determinant lies in their independence of the coordinate system in
which the matrix is expressed. Recalling that a change in coordinate system leads to a change in the
matrix representation of a transformation by a similarity transformation, the independence of trace and
determinant on coordinate system is expressed by the equations:
Tr ( S
1
AS )=Tr A
det ( S
1
AS )=det A
where S is an orthogonal matrix. Thus the trace and determinant provide numerical characteristics of a
transformation independent of any coordinate system.
Pag 52 [10]
4.4 Group representations
A representation of a symmetry group is a set of square matrices, all of the same dimension,
corresponding to the elements of the group, such that multiplication of the matrices is consistent with
the multiplication table of the group. That is, the product of matrices corresponding to two elements of
the group corresponds to that element of the group equal to the product of the two group elements in
the group itself. Representations can be of any dimension; 11 arrays are of course just ordinary
numbers.
If each group element corresponds to a different matrix, the representation is said to be faithful. A
faithful representation is a matrix group that is isomorphic to the group being represented. If the same
matrix corresponds to more than one group element, the representation, is called unfaithful. Unfaithful
representations of any group are available by assigning the number 1 to every element, or by assigning
the identity matrix of some dimension to every element. (But the number 1 is a faithful representation
of the group C1.) The collection of matrices occurring in an unfaithful representation of a group, if
taken each only once, forms a group isomorphic to a subgroup of the original group. Thus to any
unfaithful representation of a group there corresponds a faithful representation of a subgroup.
Examples of group representations:
20
21
4.5 Unitary Matrix
The following complex matrix is unitary: that its set of row vectors form an orthonormal set in C
3
:
A=
|
1
2
1i
2

1
2

i
.3
i
.3
1
.3
5i
2.15
3+i
2.15
4+3i
2.15

27 (4.5.1)
Let
r
1

r
2

r
3
be defined as follows:
r
1
=
(
1
2
,
1i
2
,
1
2
)

r
2
=
(

i
.3
,
i
.3
,
1
.3
)
r
3
=
(
5i
2.15
,
3+i
2.15
,
4+3i
2.15
)
(4.5.2)
The length of
r
1
is
r
1
=
(
r
1
r
1
)
1/2
=
|
(
1
2
)(
1
2
)
+
(
1+i
2
)(
1+i
2
)
+
(

1
2
)(

1
2
)

1/ 2
=
|
1
4
+
2
4
+
1
4

1/ 2
=1
49 (4.5.3)
For the vectors
r
2

r
3
the same.
The inner product of
r
1
r
2
is given by:
r
1
r
2
=
(
1
2
)(
i
.3
)
+
(
1+i
2
)(
i
.3
)
+
(

1
2
)(
1
.3
)
=
(
1
2
)(
i
.3
)
+
(
1+i
2
)(
i
.3
)
+
(

1
2
)(
1
.3
)
=
i
2.3

i
2.3
+
i
2.3

i
2.3
=0
(4.5.4)
Similarly, and
r
1
r
3
=0
and
r
2
r
3
=0
we can conclude that{
r
1
,
r
2
,
r
3
} is an orthonormal
set. (Try showing that the column vectors of A also form an orthonormal set in C3 .)
see [15]pag174 :
In addition the determinant of the A's is unity. The matrices representing rotations, reflections and
22
inversions are unitary follows that the matrix representations of groups are unitary.
4.6 Schur's Lemma
See pag 59 [68]:
Lemma:
In matrix form this states that any matrix which commutes with all the matrices of an irreducible
representation must be a multiple of the unit matrix, i.e.
BD( g)=D( g) B gGB=\1 (4.6.1)
To prove the identity , let b be an eigenvector of B with eigenvalue \ :
Bb=\b (4.6.2)
Then
B( D( g) b)=D( g) B b=D( g)\b=\( D( g) b) (4.6.3)
You know from quantum mechanics that if the operators commutes then they have the same
eigenvalues.
This means that D( g) b is also an eigenvector of B, with the same eigenvalue \ .
In matrix form one has to solve the equation Bb=\b , leading to the characteristic equation
det ( B\1)=0 (4.6.4)
. If we are working within the framework of complex numbers, this polynomial equation is guaranteed
to have at least one root \ , with a corresponding eigenvector b .
4.7 Great orthogonality theorem
Theorem:
Consider two unitary irreducible matrix representations I
(i )
(G) and I
( j )
(G) of a group G then:

g
I
( i)
( g)
o
I
( j )
( g)
6
=
|G
l
i
6
ij
6
o
6
6
30, 43 (4.7.1)
Where [G] is order of a group G and
l
i
is the dimension of I
(i )
(G) .
Proof:
Define the matrix M :
M

gG
I
(i )
( g) X I
( j)
( g)
(4.7.2)
Where X is some unspecified matrix. Then
23
I
( i)
( h) M=I
( i)
( h)

g
I
(i )
( g) X I
( j )
( g)
=

g
I
( i)
(hg) X I
( j )
( g)
=

hg
I
( i)
(hg) X I
( j )
(h
1
hg)
=

g
I
( i)
( g) X I
( j )
( h
1
g) (relabing hg - g)
=

g
I
( i)
( g) X I
( j )
I
( j )
(h)
=M I
( j )
(h)
(4.7.3)
By the converse of Schur's lemma , either i=j, or M=0. If i=j then by Schu's lemma M=\1=\ I
where we find m by taking the trace .

g
I
( i)
( g) X I
( j )
( g)=\6
ij
1
(4.7.4)
|G tr X =\l
(i )
So

g
I
( i)
( g) X I
( j )
( g)=
|G
l
i
6
ij
tr X 1
(4.7.5)
Or with index notations:

g
I
( i)
( g)
o
X

I
( j )
( g)
6
=
|G
l
i
6

X

6
ij
6
o6
(4.7.6)
But since
X
o
is arbitrary we chose to be also unity matrix:

g
I
( i)
( g)
o
I
( j)
( g)
6
=
| G
l
i
6

6
ij
6
o6
(4.7.7)
4.8 Great orthogonality theorem (application)
Example of the permutation group on 3 objects:
The 3! permutations of three objects form a group of order 6, commonly denoted by S
3
(symmetric
group). This group is isomorphic to the point group C
3v
, consisting of a threefold rotation axis and
three vertical mirror planes. The groups have a 2-dimensional irrep (l = 2). In the case of S
3
one usually
labels this irrep by the Young tableau = [2,1] and in the case of C
3v
one usually writes = E. In both
cases the irrep consists of the following six real matrices, each representing a single group element:
24
(
1 0
0 1
)(
1 0
0 1
)
(

1
2
.3
2
.3
2
1
2
)(

1
2

.3
2

.3
2
1
2
)(

1
2
.3
2

.3
2

1
2
)(

1
2

.3
2
.3
2

1
2
)
we have the flowing vectors:
(
V
11
V
12
V
21
V
22
)
The normalization of the (1,1) (2,2) ,(1,2)and (2,1) elements:
V
11
V
11
=

RG
6
I( R)
11

I( R)
11
=1
2
+1
2
+
(

1
2
)
2
+
(

1
2
)
2
+
(

1
2
)
2
+
(

1
2
)
2
=3
V
12
V
12
=

RG
6
I( R)
12

I( R)
12
=
2
+0
2
+
(
.3
2
)
2
+
(

.3
2
)
2
+
(
.3
2
)
2
+
(

.3
2
)
2
=3
V
21
V
21
=

RG
6
I( R)
21

I( R)
21
=0
2
+0
2
+
(
.3
2
)
2
+
(

.3
2
)
2
+
(

.3
2
)
2
+
(
.3
2
)
2
=3
V
22
V
22
=

RG
6
I( R)
22

I( R)
22
=1
2
+(1)
2
+
(
1
2
)
2
+
(
1
2
)
2
+
(

1
2
)
2
+
(

1
2
)
2
=3
(4.8.1)
The orthogonality of the (1,1) and (2,2) elements:
V
11
V
22
=

RG
6
I( R)
11

I( R)
22
=1
2
+(1)(1)+
(

1
2
)(
1
2
)
+
(

1
2
)(
1
2
)
+
(

1
2
)
2
+
(

1
2
)
2
=0. (4.8.2)
Similar relations hold for the orthogonality of the elements (1,1) and (1,2), etc. One verifies easily in
the example that all sums of corresponding matrix elements vanish because of the orthogonality of the
given irrep to the identity irrep.
4.9 D
3
representations and irreducible representations
See [69]pag 66:
A matrix representation of a group is defined as a set of square, nonsingular matrices (matrices with
nonvanishing determinants) that satisfy the multiplication table of the group when the matrices are
multiplied by the ordinary rules of matrix multiplication. There are other kinds of representations (see
Section 6.1) but unless there is a specific statement to that effect, it will be understood that a
representation means a matrix representation.
We give several examples of representations of the group D3:
I
(1)
( E)=I
( 1)
( A)=I
( 1)
( B)=I
( 1)
(C)=I
(1)
( D)=I
( 1)
( F)=1 28 (4.9.1)
This is a one-dimensional representation (lxl matrices) which obviously satisfies the group
multiplication table. It appears to be trivial but nevertheless plays an important role in later
developments. This representation is called the totally symmetric representation or the unit
representation. Another one-dimensional representation is
I
( 2)
( E)=I
(2)
( A)=I
( 2)
( B)=I
( 2)
(C)=1, I
( 2)
( D)=I
( 2)
( F )=1 (4.9.2)
25
A two-dimensional representation consisting of 2 x 2 matrices is:
I
(3)
( E)=
(
1 0
0 1
)
I
(3)
( A)=
(
1 0
0 1
)

I
(3)
( B)=
(
1/ 2 .3/ 2
.3/ 2 1/ 2
)
28,31
I
(3)
(C)=
(
1/ 2 .3/ 2
.3/ 2 1/ 2
)
I
(3)
( D)=
(
1/ 2 .3/ 2
.3/ 2 1/ 2
)
I
(3)
( F)=
(
1/ 2 .3/ 2
.3/ 2 1/ 2
)
(4.9.3)
We may therefore regard these matrices as a three-dimensional representation of D
3
:
I have calculated in Mathematica (4.11.31) and here I found a lot of mistakes in Weissbluth the correct
are:
I
( 4)
( E)=
(
1 0 0
0 1 0
0 0 1
)
I
( 4)
( A)=
(
1 0 0
0 1 0
0 0 1
)
I
( 4)
( B)=
(
1/ 2 .3/ 2 0
.3/ 2 1/ 2 0
0 0 1
)
I
( 4)
(C)=
(
1/ 2 .3/ 2 0
.3/ 2 1/ 2 0
0 0 1
)
35
I
( 4)
( D)=
(
1/ 2 .3/ 2 0
.3/ 2 1/ 2 0
0 0 1
)
I
( 4)
( F)=
(
1/ 2 .3/ 2 0
.3/ 2 1/ 2 0
0 0 1
)
(4.9.4)
Another three-dimensional representation is the set
I
(5)
( E)=
(
1 0 0
0 1 0
0 0 1
)
I
(5)
( A)=
(
1 0 0
0 0 1
0 1 0
)
I
(5)
(C)=
(
0 0 1
0 1 0
1 0 0
)
I
(5)
( B)=
(
0 1 0
1 0 0
0 0 1
)
I
(5)
( D)=
(
0 0 1
1 0 0
0 1 0
)
I
(5)
( F)=
(
0 1 0
0 0 1
1 0 0
)
29
(4.9.5)
The number of representations that may be constructed is without limit; as a final example we show a
six-dimensional representation:
26
I
(6)
( E)=
(
1 0 0 0 0 0
0 1 0 0 0 0
0 0 1 0 0 0
0 0 0 1 0 0
0 0 0 0 1 0
0 0 0 0 0 1
)
I
(6)
( A)=
(
1 0 0 0 0 0
0 1 0 0 0 0
0 0 1 0 0 0
0 0 0 1 0 0
0 0 0 0 1 0
0 0 0 0 0 1
)
I
(6)
( B)=
(
1/ 2 .3/ 2 0 0 0 0
.3/ 2 1/ 2 0 0 0 0
0 0 1/ 2 .3/ 2 0 0
0 0 .3/ 2 1/ 2 0 0
0 0 0 0 1 0
0 0 0 0 0 1
)
I
(6)
(C)=
(
1/ 2 .3/ 2 0 0 0 0
.3/ 2 1/ 2 0 0 0 0
0 0 1/ 2 .3/ 2 0 0
0 0 .3/ 2 1/ 2 0 0
0 0 0 0 1 0
0 0 0 0 0 1
)
I
(6)
( D)=
(
1/ 2 .3/ 2 0 0 0 0
.3/ 2 1/ 2 0 0 0 0
0 0 1/ 2 .3/ 2 0 0
0 0 .3/ 2 1/ 2 0 0
0 0 0 0 1 0
0 0 0 0 0 1
)
I
(6)
( F)=
(
1/ 2 .3/ 2 0 0 0 0
.3/ 2 1/ 2 0 0 0 0
0 0 1/ 2 .3/ 2 0 0
0 0 .3/ 2 1/ 2 0 0
0 0 0 0 1 0
0 0 0 0 0 1
)
(4.9.6)
If the matrices belonging to a representation I are subjected to a similarity transformation, the
result is a new representation I ' . The two representations I and I ' are said to be equivalent.
If I and I ' cannot be transformed into one another by a similarity transformation, I and
I ' are then said to be inequivalent. It may be shown (eq.(4.5.1)) that for a finite group every
representation is equivalent to a unitary representation (i.e., consisting entirely of unitary matrices). We
shall assume henceforth that all representations are unitary unless the contrary is explicitly stated (see
also Section 3.4).
An important notion concerning representations is that of reducibility. Consider, for example
27
I
(6)
( B) in (4.9.6):
I
(6)
( B)=
(
1/ 2 .3/ 2 0 0 0 0
.3/ 2 1/ 2 0 0 0 0
0 0 1/ 2 .3/ 2 0 0
0 0 .3/ 2 1/ 2 0 0
0 0 0 0 1 0
0 0 0 0 0 1
)
(4.9.7)
This matrix consists of four separate blocks along the main diagonaltwo of the blocks are two-
dimensional and the other two are one-dimensional. Moreover, examination of the separate blocks
reveals that the two- dimensional blocks are identical with the representation matrix I
(3)
( B)
[Eq. (4.9.3)] and the one-dimensional blocks coincide with I
(1)
( B) [Eq. (4.9.1)]. Therefore
I
(6)
( B) is said to be reducible into 2 I
(3)
( B) and 2 I
(1)
( B) . Symbolically this is expressed by
I
(6)
( B)=2 I
( 3)
( B)+2I
( 1)
( B)
I
(6)
( B)=2 I
( 3)
( B)2I
(1)
( B)
(4.9.8)
in which the right side of the equation signifies that I
(3)
( B) appears twice and I
(1)
( B) appears
twice along the main diagonal in (4.9.7). In this context the symbol + clearly has nothing to do with
addition. The symbol is also used which means direct sum.
The character is denoted by X
( j )
( R) , thus
X
( j )
( R)=

o
I
oo
( j )
( R)
(4.9.9)
Table 1.1 Character table of D
3 31
E A B C D F
I
(1)
I
( 2)
I
(3)
1
1
2
1
-1
0
1
-1
0
1
-1
0
1
1
-1
1
1
-1
4.10 Basis Functions
The representations of a group are intimately connected with sets of functions called basis functions. A
few examples will help to establish the central idea. Let

1
( r)=x ,
2
(r)=y
(4.10.1)
We now inquire as to how these functions are altered under the coordinate transformations E, A,. .., F
which are elements of the group D
3
. Under any coordinate transformation described by r ' =Rr (R is
a matrix of rotations(see (4.2.4),(5.2.14))), a function f (r) transforms in accordance with
P
R
f ( r )=f ( R
1
r) (4.10.2)
28
For R=E we obtain trivially,
P
E

1
(r)=
1
(r)=x , P
E

2
( r)=
2
( r )=y
(4.10.3)
Or in matrix form:
P
E
(
1,

2
)=(
1,

2
)
(
1 0
0 1
)
(4.10.4)
The general statement is that a set of linearly independent functions
1
( j)
( r) ,
2
( j )
(r) ,... ,
n
( j )
(r) are
basis functions for the I
( j )
representations of a group if
P
R

k
( j )
(r)=

\=1
n

\
( j )
(r) I
\k
( j )
( R) 29,30, 40 (4.10.5)
For all the elements of the group R.
The basis set for a representation consists of linearly independent functions. These can always be
chosen so as to be orthonormal, i.e.,

l
j
( r)
k
j
( r)=6
lk
(4.10.6)
From (4.10.5),

l
j
( r )P
R

k
j
( r ) =

\

l
j
(r)
k
j
(r) I
\k
( j)
( R)=I
l k
( j )
( R) P
R

k
j
( r)=

\=1
n

\
j
( r)I
\k
( j)
(4.10.7)
4.11 Projection Operators (D
3
)
We will prove that see(4.11.31):
I
(5)
=I
(3)
+I
(1)
31 (4.11.1)
It is pertinent to inquire what relations, if any, exist between the basis functions of I
(5)
and the basis
functions of the component irreducible representations I
(3)
and I
(1)
. Suppose (f
l
,f
2
,f
3
) is the set
of (normalized) basis functions of I
(5)
[Eq. (4.9.5)]. It follows, from the definition of basis
functions (4.10.5),that
29
P
E
( f
1,
f
2,
f
3
)=( f
1,
f
2,
f
3
)
(
1 0 0
0 1 0
0 0 1
)
=( f
1,
f
2,
f
3
)
P
A
( f
1,
f
2,
f
3
)=( f
1,
f
2,
f
3
)
(
1 0 0
0 0 1
0 1 0
)
=( f
1,
f
3,
f
2
)
P
B
( f
1,
f
2,
f
3
)=( f
1,
f
2,
f
3
)
(
0 0 1
0 1 0
1 0 0
)
=( f
3,
f
2,
f
1
)
P
C
( f
1,
f
2,
f
3
)=( f
1,
f
2,
f
3
)
(
0 1 0
1 0 0
0 0 1
)
=( f
2,
f
1,
f
3
)
P
D
( f
1,
f
2,
f
3
)=( f
1,
f
2,
f
3
)
(
0 0 1
1 0 0
0 1 0
)
=( f
2,
f
3,
f
1
)
P
F
( f
1,
f
2,
f
3
)=( f
1,
f
2,
f
3
)
(
0 1 0
0 0 1
1 0 0
)
=( f
3,
f
1,
f
2
) 32
(4.11.2)
Where we have multiplied the row with matrix = row.
Let
k
j
(r) be a basis function belonging to the jth irreducible representation I
( j )
see(4.10.5).
Then, by definition,
P
R

k
j
( r)=

\=1
n

\
( j )
(r ) I
\k
( j )
( R) (4.11.3)
Multiplying through by I
\ ' k '
( j )
( R)

and summing over R, we obtain

R
I
\' k '
( j ' )
( R)

P
R

k
( j )
(r)=

R

\=1
l
j
I
\' k '
( j ' )
( R)

\
( j )
(r )I
\k
( j )
( R)
=
h
l
j

\

\
( j)
6
jj '
6
\\'
6
kk '
=
h
l
j

\'
( j)
6
jj '
6
kk '
(4.11.4)
in which the second and third equalities are a consequence of the orthogonality theorem (4.7.1). We
may now define an operator
P
\k
( j )
=
l
j
h

R
I
\k
( j )
( R)

P
R
48 (4.11.5)
Having the property from (4.11.4):
30
P
\k
( j )

l
( i)
=
\
(i )
6
ij
6
lk
(4.11.6)
Or when i=j and l=k,
P
\k
( j )

k
( j )
=
\
( j )
(4.11.7)
When \=k (4.11.6) becomes
P
k k
( j )

l
( i)
=
k
(i )
6
ij
6
lk
(4.11.8)
Or
P
k k
( j )

k
( j )
=
k
( j)

P
k k
( j )

l
( j )
=0, i j , l k
(4.11.9)
From (4.11.9) it is seen that
k
( j)
is an eigenvector of P
k k
( j )
with eigenvalue equal to one. Also
(P
k k
( j)
)
2

k
( j )
=P
k k
( j )

k
( j )
=
k
( j)
(4.11.10)
So that
(P
k k
( j)
)
2
=P
k k
( j )
=
l
j
h

R
I
k k
( j )
( R)

P
R
(4.11.11)
P
k k
( j )
is known as a projection operator; operators that obey a relation of the type O
2
= O are said to
be idempotent. From (3.5-14) we see that projection operators are idempotent.
If one now sums P
k k
( j )
over k, then, from (4.11.11),

k
P
k k
( j )
P
( j )
=
l
j
h

R

k
I
k k
( j)
( R)

P
R
=
l
j
h

R
X
( j)
( R)

P
R
(4.11.12)
P
( j )
Is also a projection operator(for example I
kk
(3)
is a matrix 2x2 (4.9.3) and kk= 11,12,21,22).
Illustration of (4.11.12) :
P
(1)
=
l
1
h

R
X
( 1)
P
R
=
1
6
|
P
E
+P
A
+P
B
+P
C
+P
D
+P
F
32
P
( 2)
=
l
1
h

R
X
(1)
P
R
=
1
6
|
P
E
P
A
P
B
P
C
+P
D
+P
F

P
( 3)
=
2
6
|
2P
E
P
D
P
F

(4.11.13)
We will prove (4.11.1) by using (4.11.12) we will generate the basis functions for I
(3)
in the
decomposition of I
(5)
as is given by (4.11.1) . From (4.9.3) or Table 1.1 Character table of D3 31 we
have
X
(3)
( E)=2, X
(3)
( A)=X
( 3)
( B)=X
( 3)
(C)=0, X
( 3)
( D)=X
(3)
( F )=1 (4.11.14)
31
Therefore using (4.11.2), (for example
P
D
f
2
=f
3
) we get:
P
( 3)
f
1
=
2
6
|
2P
E
f
1
P
D
f
1
P
F
f
1

=
1
3
| 2 f
1
f
2
f
3
h
1

P
(3)
f
2
=
2
6
|
2P
E
f
2
P
D
f
2
P
F
f
2

=
1
3
| 2 f
2
f
3
f
1
h
2
P
(3)
f
3
=
2
6
|
2P
E
f
3
P
D
f
3
P
F
f
3

=
1
3
| 2 f
3
f
1
f
2
h
3
39
(4.11.15)
The three functions h1,h2, and h3 are not independent since hl + h2 + h3 = 0. Hence there are only two
independent functions and these may be constructed in an infinite number of ways. The choice
corresponding to (3.5-3), after normalization, is g2 = h1 and g3 = h3 h2.
So we have
g
2
=
1
3
| 2 f
1
f
2
f
3

33,39 (4.11.16)
And
g
3
=h
3
h
2
=
1
3
| 2 f
3
f
1
f
2

1
3
| 2 f
2
f
3
f
1
=f
2
+ f
3
33 ,39 (4.11.17)
In similar way taking into account that for first equation in (4.11.13) all characters are equal to one :
P
(1)
f
1
=
l
1
h

R
X
(1)
P
R
f
1
=
1
6
|
P
E
f
1
+P
A
f
1
+P
B
f
1
+P
C
f
1
+P
D
f
1
+P
F
f
1

=
1
3
|
f
1
+ f
2
+ f
3

P
( 1)
f
2
=
1
3
|
f
1
+ f
2
+f
3

P
( 1)
f
3
=
1
3
|
f
1
+f
2
+ f
3

(4.11.18)
Thus we get for
g
1
g
1
=
1
3
|
f
1
+ f
2
+ f
3
33 (4.11.19)
In what follows we will normalise applying the procedure described at pag 248 [72] or pag 141,248
[40] or pag 63,61[31] or 214,230 [73] or pag 588 [69] :
1=

( N 1)

( N 1)d t
(4.11.20)
32
1=N
2

( c
1

+c
2

)( c
1

1
+c
2

2
) d t

1=N
2

( c
1
2

1
2
d t+2c
1
c
2

2
d t+c
2
2

2
2
d t)
(4.11.21)
1=N
2
(c
1
2
+2c
1
c
2

2
d t+c
2
2
)
1=N
2
(c
1
2
+2c
1
c
2
S
12
+c
2
2
)
N=
1
.
(c
1
2
+2c
1
c
2
S
12
+c
2
2
)
(4.11.22)
Where
S
12
=

2
d t
(4.11.23)
Is the overlap integral.
Thus the normalisation for (4.11.19) is:

|
f
1
+f
2
+ f
3

N
3

N
3
|
f
1
+ f
2
+ f
3

=
N
2
9
(
f
1
f
1
+ f
2
f
2
+ f
3
f
3
+2 f
1
f
2
+2 f
1
f
3
+2 f
2
f
3

)
=
N
2
9
( 3+6S)=1

thus
N=
3
.3+6S
(4.11.24)
The normalisation for (4.11.16):

| 2 f
1
f
2
f
3

N
3

N
3
| 2 f
1
f
2
f
3

=
N
2
9
(
4 f
1
f
1
+ f
2
f
2
+ f
3
f
3
4 f
1
f
2
4 f
1
f
3
+2 f
2
f
3

)
=
N
2
9
( 4+28S+2S)=1

thus
N=
3
.66S
(4.11.25)
And the normalisation for (4.11.17):
33

|f
2
f
3
N

N |f
2
f
3

=N
2
(
f
2
f
2
+ f
3
f
3
2 f
2
f
3

)
=N
2
( 22S)=1

thus
N=
1
.22S
(4.11.26)
If we put all together we get (see [1])
g
1
=
1
3
3
.3+6S
|
f
1
+f
2
+ f
3

g
2
=
1
3
3
.66S
| 2 f
1
f
2
f
3

g
3
=
1
.22S
|f
2
+f
3

(4.11.27)
Or if we put overlap integrals to be zero we get
g
1
=
1
.3
|
f
1
+ f
2
+ f
3

g
2
=
1
.6
| 2 f
1
f
2
f
3

g
3
=
1
.2
|f
2
+ f
3

(4.11.28)
Now we can construct the unitary matrix S and S
1
see pag 56 [71] :
| g
1
, g
2
, g
3
=| f
1
, f
2
, f
3
S
(4.11.29)
(
1
.3
2
.6
0
1
.3

1
.6

1
. 2
1
.3

1
.6
1
.2
)
and see [11] pag 19:
I ' (G)=S
1
I(G) S 42 (4.11.30)
1) The matrix in order to obtain
5
=
1
+
3

34
S={ {
1
.3
,
2
.6
, 0}, {
1
.3
,
1
.6
,
1
.2
} , {
1
.3
,
1
.6
,
1
.2
}};

S1=Inverse| S ;
MatrixForm| S1 . MatrixForm| C . MatrixForm| S
=MatrixForm| S1. C. S ,TableSpacing-{1 , 2}

for I
(5)
( B)
(
1
.3
1
.3
1
.3
.2
3
1
.6
1
.6
0
1
.2
1
. 2
)
(
0 1 0
1 0 0
0 0 1
)
(
1
.3
. 2
3
0
1
.3
1
.6
1
.2
1
.3
1
.6
1
.2
)
=
(
1 0 0
0
1
2
.3
2
0
.3
2
1
2
)

for I
(5)
(C)
(
1
.3
1
.3
1
.3
.2
3
1
.6
1
.6
0
1
.2
1
. 2
)
(
0 0 1
0 1 0
1 0 0
)
(
1
.3
.2
3
0
1
.3
1
.6
1
.2
1
.3
1
.6
1
.2
)
=
(
1 0 0
0
1
2
.3
2
0
.3
2
1
2
)

for I
(5)
( A)
(
1
.3
1
.3
1
.3
.2
3
1
.6
1
.6
0
1
.2
1
. 2
)
(
1 0 0
0 0 1
0 1 0
)
(
1
.3
. 2
3
0
1
.3
1
.6
1
.2
1
.3
1
.6
1
.2
)
=
(
1 0 0
0 1 0
0 0 1
)

2) We put here other matrix in order to obtain
5
=
3
+
1
29,26 (4.11.31)
I
(5)
( B)
here I corrected at pag 69 [69]:because Weissbluth had mistaken the correct is M I
( 5)
( B) M
1
:
35
(
.2
3
1
.6
1
.6
0
1
. 2
1
.2
1
.3
1
.3
1
.3
)
(
0 1 0
1 0 0
0 0 1
)
(
.2
3
0
1
.3
1
.6
1
.2
1
.3
1
.6
1
.2
1
.3
)
=
(
1
2
.3
2
0
.3
2
1
2
0
0 0 1
)
42 (4.11.32)

for I
(5)
( D)
(
.2
3
1
.6
1
.6
0
1
. 2
1
.2
1
.3
1
.3
1
.3
)
(
0 1 0
0 0 1
1 0 0
)
(
.2
3
0
1
.3
1
.6
1
.2
1
.3
1
.6
1
.2
1
.3
)
=
(
1
2
.3
2
0
.3
2
1
2
0
0 0 1
)

for I
(5)
( A)
(
.2
3
1
.6
1
.6
0
1
. 2
1
.2
1
.3
1
.3
1
.3
)
(
1 0 0
0 0 1
0 1 0
)
(
.2
3
0
1
.3
1
.6
1
.2
1
.3
1
.6
1
.2
1
.3
)
=
(
1 0 0
0 1 0
0 0 1
)

4.12 Symmetry adapted linear combinations(C
3v
)
See [11]:Once we know the irreps spanned by an arbitrary basis set, we can work out the appropriate
linear combinations of basis functions that transform the matrix representatives of our original
representation into block diagonal form (i.e. the symmetry adapted linear combinations). Each of the
SALCs transforms as one of the irreps of the reduced representation. We have already seen this in our
D
3
example. The two linear combinations of A1 symmetry were sN and s1 + s2 + s3, both of which are
symmetric under all the symmetry operations of the point group. We also chose another pair of
functions, 2s1 s2 s3 and s2 s3, which together transform as the symmetry species E.
Example: a matrix representation of the
C
3v
point group (the ammonia molecule)
The first thing we need to do before we can construct a matrix representation is to choose a basis. For
NH
3
, we will select a basis
( s
N
, s
1,
s
2,
s
3
)
that consists of the valence s orbitals on the nitrogen
and the three hydrogen atoms. We need to consider what happens to this basis when it is acted on by
each of the symmetry operations in the
C
3v
point group, and determine the matrices that would be
required to produce the same effect. The basis set and the symmetry operations in the
C
3v
point
group are summarised in the Fig. 3 below.
36
E (sN,s1,s2,s3) (sN,s1,s2,s3)
C
3
+
(sN,s1,s2,s3) (sN,s2,s3,s1)
C
3

(sN,s1,s2,s3) (sN,s3,s1,s2)

v
(sN,s1,s2,s3) (sN,s1,s3,s2)

v
'
(sN,s1,s2,s3) (sN,s2,s1,s3)

v
' '
(sN,s1,s2,s3) (sN,s3,s2,s1)
in Matrix form:
the matrices that carry out the same transformations are:
(E) ( s
N
, s
1,
s
2,
s
3
)
(
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
)
=( s
N
, s
1,
s
2,
s
3
)
( C
3
+
) ( s
N
, s
1,
s
2,
s
3
)=
(
1 0 0 0
0 0 0 1
0 1 0 0
0 0 1 0
)
=(s
N
, s
2,
s
3,
s
1
)
( C
3

) ( sN , s1 , s2 , s3)
(
1 0 0 0
0 0 1 0
0 0 0 1
0 1 0 0
)
=( s
N
, s
3,
s
1,
s
2
)
(

v
) ( s
N
, s
1,
s
2,
s
3
)
(
1 0 0 0
0 1 0 0
0 0 0 1
0 0 1 0
)
=( s
N
, s
1,
s
3,
s
2
)
37
Fig. 3
(

v
'
) ( s
N
, s
1,
s
2,
s
3
)
(
1 0 0 0
0 0 1 0
0 1 0 0
0 0 0 1
)
=( s
N
, s
2,
s
1,
s
3
)
(

v
' '
) ( s
N
, s
1,
s
2,
s
3
)
(
1 0 0 0
0 0 0 1
0 0 1 0
0 1 0 0
)
=( s
N
, s
3,
s
2,
s
1
)
In the table form:
sN s1 s2 s3
E sN s1 s2 s3
C
3
+
sN s2 s3 s1
C
3

sN s3 s1 s2

v
sN s1 s3 s2

v
'
sN s2 s1 s3

v
' '
sN s3 s2 s1
To determine the SALCs of A1 symmetry, we multiply the table through by the characters of the A1
irrep (all of which take the value 1). Summing the columns gives
sN + sN + sN + sN + sN + sN = 6sN
s1 + s2 + s3 + s1 + s2 + s3 = 2(s1 + s2 + s3)
s2 + s3 + s1 + s3 + s1 + s2 = 2(s1 + s2 + s3)
s3 + s1 + s2 + s2 + s3 + s1 = 2(s1 + s2 + s3)
Apart from a constant factor (which doesnt affect the functional form and therefore doesnt affect the
symmetry properties), these are the same as the combinations we determined earlier. Normalising gives
us two SALCs of A1 symmetry.

1
=s
N

2
=
1
.3
( s
1
+s
2
+s
3
)
(4.12.1)
We now move on to determine the SALCs of E symmetry. Multiplying the table above by the
appropriate characters for the E irrep gives
sN s1 s2 s3
E 2sN 2s1 2s2 2s3
C
3
+
-sN -s2 -s3 -s1
C
3

-sN -s3 -s1 -s2

v
0 0 0 0
38

v
'
0 0 0 0

v
' '
0 0 0 0
Summing the columns yields
2sN sN sN = 0
2s1 s2 s3
2s2 s3 s1
2s3 s1 s2
and this is equivalent with previous derivation (4.11.15),(4.11.16) and (4.11.17):

3
=
1
.6
( 2s
1
s
2
s
3
)

4
=
1
.2
( s
2
s
3
)

(4.12.2)
4.13 Bonding in polyatomics - constructing molecular orbitals from
SALCs
In the previous section we showed how to use symmetry to determine whether two atomic orbitals can
form a chemical bond. How do we carry out the same procedure for a polyatomic molecule, in which
many atomic orbitals may combine to form a bond? Any SALCs of the same symmetry could
potentially form a bond, so all we need to do to construct a molecular orbital is take a linear
combination of all the SALCs of the same symmetry species.
The general procedure is:
1. Use a basis set consisting of valence atomic orbitals on each atom in the system.
2. Determine which irreps are spanned by the basis set and construct the SALCs that transform as each
irrep.
3. Take linear combinations of irreps of the same symmetry species to form the molecular orbitals.
e.g. in our
NH
3
example we could form a molecular orbital of
A
1
symmetry from the two
SALCs that
transform as
A
1
,
1( A
1
)=c
1

1
+c
2

2
=c
1
s
N
+c
2
1
.3
( s
1
+s
2
+s
3
)
(4.13.1)
Unfortunately, this is as far as group theory can take us. It can give us the functional form of the
molecular orbitals but it cannot determine the coefficients c1 and c2. To go further and obtain the
expansion coefficients and orbital energies, we must turn to quantum mechanics.
39
4.14 Product representations
Consider the two matrices(see pag 83 [69] )
The direct product of two matrices (given the symbol ) is a special type of matrix product that generates
a matrix of higher dimensionality if both matrices have dimension greater than one. The easiest way to
demonstrate how to construct a direct product of two matrices A and B is by an example:
AB=
(
a
11
a
12
a
21
a
22
)

(
b
11
b
12
b
21
b
22
)
=
(
a
11
B a
12
B
a
21
B a
22
B
)
=
(
a
11
(
b
11
b
12
b
21
b
22
)
a
12
(
b
11
b
12
b
21
b
22
)
a
21
(
b
11
b
12
b
21
b
22
)
a
22
(
b
11
b
12
b
21
b
22
)
)
=
(
a
11
b
11
a
11
b
12
a
12
b
11
a
12
b
12
a
11
b
21
a
11
b
22
a
12
b
21
a
12
b
22
a
21
b
11
a
21
b
12
a
22
b
11
a
22
b
12
a
21
b
21
a
21
b
22
a
22
b
21
a
22
b
22
)
The characters of A , B and AxB are evidently related by
X( AB)=X( A)X( B) (4.14.1)
Now let
(
1
,
2
)
be a set of basis function,s for a two dimensional irreducible representation I
(j)
of a group G and let
(
1
,
2
)
similarly belong to I
(+)
of G. This mean , according to (4.10.5)
that:
P
R

1
=
1
I
11
(j)
( R)+
2
I
21
( j)
( R)
P
R

2
=
1
I
12
(j)
( R)+
2
I
22
( j)
( R)
(4.14.2)
With analogous relations for
(
1
,
2
)
.Therefore,
P
R
(
1

1
)=|
1
I
11
(j)
( R)+
2
I
21
( j)
( R) |
1
I
11
( +)
( R)+
2
I
21
( +)
( R)
=
1

1
I
11
( j)
( R) I
11
( +)
( R)+
1

2
I
11
(j)
( R) I
21
(+)
( R)
+
2

1
I
21
( j)
( R) I
11
( +)
( R)+
2

2
I
21
(j)
( R)I
21
( +)
( R)
(4.14.3)
And continuing in the same fashion it is found that
P
R
(
1

1
,
1

2
,
2

1
,
2

2
)
=(
1

1
,
1

2
,
2

1
,
2

2
)
(
I
11
(j)
I
11
(+)
I
11
(j)
I
12
(+)
I
12
(j)
I
11
(+)
I
12
(j)
I
12
(+)
I
11
(j)
I
21
(+)
I
11
(j)
I
22
(+)
I
12
(j)
I
21
(+)
I
12
(j)
I
22
(+)
I
21
(j)
I
11
(+)
I
21
(j)
I
12
(+)
I
22
(j)
I
11
(+)
I
22
(j)
I
12
(+)
I
21
(j)
I
21
(+)
I
21
(j)
I
22
(+)
I
22
(j)
I
21
(+)
I
22
(j)
I
22
(+)
)
41 (4.14.4)
We can see that (4.14.3) is the first column of (4.14.4).
40
Hence it may be concluded that the four product functions

1
,
1

2
,
2

1
,
2

2
are basis
functions for a representationcalled a product representationof the group G. The product
representation I
(j+)
I
( j)
I
( +)
is generally reducible even if I
(j)
and I
(+)
are irreducible. As
in (4.14.1),
X
(j+)
( R)=X
(j)
( R) X
( +)
( R) (4.14.5)
This result can be formalised by writing
P
R
(
j
(j)

l
( +)
)=

ik

i
(j)

k
(+)
I
ij
(j)
( R)I
kl
(+)
( R)
=

ik

i
( j)

k
( +)
| I
(j)
( R)I
(+)
( R)
ik , jl
=

ik

i
( j)

k
( +)
I
ik , jl
( j+)
( R)
43 (4.14.6)
And
X
(j+)
( R)=

ij
I
ii
( j)
( R)I
jj
(+)
( R)
(4.14.7)
It is sometimes useful to regard
(
1
,
2
)
and
(
1
,
2
)
the basis sets for I
(j)
and I
(+)
,
respectivelyas the components of two-dimensional vectors.
An important case arises when j=+ ; then the two representations forming the product
representation are the same. As before, let both
(
1
,
2
)
and
(
1
,
2
)
belong to I
(j)
(=
I
(+)
). It should be kept in mind that

1
and

2
are partners, as are

1
and

2
, but
there is no partnership relation between any of the 's with any of the 's. From (4.14.4) ,
(4.14.3) we find (with the superscript j suppressed)
P
R
(
1

1
)=
1

1
| I
11
( R)
2
+(
1

2
+
2

1
) I
11
( R) I
21
( R)
+
2

2
| I
21
( R)
2
(4.14.8)
P
R
(
1

1
+
2

1
)=2
1

1
I
11
( R)I
12
( R)
+(
1

2
+
2

1
)| I
11
( R)I
22
( R)+I
12
( R) I
21
( R)
+2
2

2
I
21
( R)I
22
( R)
(4.14.9)
P
R
(
2

2
)=
1

1
| I
12
( R)
2
+(
1

2
+
2

1
) I
12
( R) I
22
( R)
+
2

2
| I
22
( R)
2
(4.14.10)
P
R
(
1

1
)=(
1

1
)| I
11
( R)I
22
( R)I
12
( R) I
21
( R)
(4.14.11)
The products

1
,

2
+
2

1
,

2

2
are symmetric products in the sense that they remain
unchanged under an interchange of indices. The product

1
is antisymmetric. From
(4.14.8)-(4.14.11) it is seen that the symmetric products transform among themselves and do not mix
with the antisymmetric product and vice versa. This feature may be expressed by writing
I
(j)
I
(j)
=( I
( j)
I
(j)
)
+
+(I
(j)
I
(j)
)
-
(4.14.12)
where (I
(j)
I
( j)
)
+
stands for the product representation whose basis functions are symmetric
41
products; (I
(j)
I
( j)
)
+
is called the symmetric product representation; (I
(j)
I
( j)
)
-
, the product
representation whose basis functions are antisymmetric, is called the antisymmetric product
representation.
4.15 Clebsch-Gordan coefficients for simply reducible groups (CGC)
See pag 61 [70] :
Equivalent representations
We have seen in (4.11.30) and example (4.11.32) that on changing the basis by a nonsingular matrix S ,
an operator P transforms according to P' =S
1
P S . This leads us to the following definition:
Two REPs ={P
R
|R2G} and ' ={P'
R
|
RG
} of a group G
are equivalent or similar , if every P
R
and P'
R
there exists a nonsingular operator S such that
P' =S
1
P S
for each a2G
Let
{ f
i
' }
be the new basis . Then in the matrix REP we have,
f
i
' =

j
S
ij
f
j
(4.15.1)
P
R
f
i
' =

J
S
ij
P
R
f
i
=

jk
S
ji
I
kj
( R) f
k
=

jkl
S
ji
I
kj
( R)(S
1
) f
l
' =

l
(S
1
I( R) S)
li
f
l
'
(4.15.2)
Therefore
I ' ( R)=S
1
I( R) S = (4.11.30) (4.15.3)
The reduction of I
(o)
is achieved according to (4.15.3) by a non-singular matrix C
o
(we will
use C-Clebsch instead of S ), wich transform the basis e
i
( o)
e
k
( )
into a new basis
e
l
( s )
s=1,2,. .. ,(o) . The matrix elements of C
o
are denoted by
(
o
i k

s
l
)
and called
Clebsch-Gordan or Wigner coefficients (CGC). Then
e
l
( s)
=

ik
(
o
i k

s
l
)
e
i
(o)
e
k
()
(4.15.4)
Or in notations of [75] :
42

l
( s )
=

ik
(
o
i k

s
l
)

i
( o)

k
()
48 (4.15.5)
Diagonal form
(C
o
)
1
I
( o)
C
o
=

I
( ,1)
I
( , s)
...

(4.15.6)
If the basis systems e
i
( o)
e
k
( )
and e
l
( , s)
are orthonormal then C
o
is unitary and the CGC
obey

ik
(
o
i k

' s '
l '
)(
o
i k

s
l
)
=6
'
6
ss'
6
l l '

s l
(
o
i k

s
l
)(
o
i ' k '

s
l
)

=6
ii'
6
kk '
(4.15.7)
And therefore also
e
i
(o)
e
k
()
=

ik
(
o
i k

s
l
)

e
l
( s )
(4.15.8)
Or in notations of [75] :

i
( o)

k
()
=

ik
(
o
i k

s
l
)

l
(s )
(4.15.9)
Multiplying both sides of (4.15.6) with
C
o
and (C
o
)
1
we get
I
(o)
=C
o
I
( , s)
(C
o
)
1
(4.15.10)
But from (4.14.6) we have also
I
ik , jl
(o)
( R)=I
ij
( o)
( R) I
kl
( )
( R) (4.15.11)
Equating (4.15.10) and (4.15.11) we obtain,
I
ij
(o)
( R) I
kl
( )
( R)=

s ,mn
(
o
i k

s
m
)
I
mn
( s)
( R)
(
o
j l

s
n
)

(4.15.12)
Multiplying this by I
m' n'
( ' )
( R) and summing over all
RG
, we obtain with (4.7.1):

s
(
o
i k

s
m
)(
o
j l

s
n
)

=
l

h

RG
I
ij
( o)
( R) I
kl
( )
( R) I
mn
()
( R) (4.15.13)
As particular case for (4.15.13) see pag 104 [74]with j =i , l =k and n=m have:
43
(
o
j l

n
n
)
=

h

RG
I
jj
( o)
( R) I
l l
( )
( R) I
nn
( )
( R)

1/ 2
(4.15.14)
Substituting in (4.15.14) we get:

s
(
o
i k

s
m
)

h

RG
I
jj
(o)
( R) I
l l
()
( R) I
nn
()
( R)

1/ 2
=
l

h

RG
I
ij
( o)
( R) I
kl
( )
( R) I
mn
( )
( R)
(
o
i k

s
m
)
=
l

h

RG
I
ij
(o)
( R)I
kl
( )
( R) I
mn
()
( R)

h

RG
I
jj
(o)
( R)I
l l
( )
( R) I
nn
()
( R)

1/2
(
o
i k

s
m
)
=
.
l

h

RG
I
ij
( o)
( R) I
kl
( )
( R)I
mn
( )
( R)
.

RG
I
jj
(o)
( R)I
l l
( )
( R) I
nn
( )
( R)
51
(4.15.15)
For other forms of (4.15.15) see [75] and [76] .
Illustration (4.15.15):
we have a table from Lenef [1]:
Table 1.2 Irreducible representations of the group
C
3v
C
3v
E C
3
C
3
' c
va
c
vb
c
vc
A
1
1 1 1 1 1 1
A
2
1 1 1 -1 -1 -1
E
(
1 0
0 1
)
(

1
2
.3
2

.3
2

1
2
) (
1
2

.3
2
.3
2

1
2
)
(
1 0
0 1
)
(

1
2

.3
2

.3
2
1
2
) (

1
2
.3
2
.3
2
1
2
)
we will multiply approximately(or slightly different ) like in great orthogonality theorem
(
E E
11

A
1
s
1
)
=
.
l

h

R=1
6
I
11
( E)
( R) I
11
( E)
( R) I
11
( A
1
)
( R)
.

R=1
6
I
11
( E)
( R)I
11
( E)
( R) I
11
( A
1
)
( R)
l

=1
this is the dimension of
A
1
h=6 number of the groups
44
i k=
(
11 12
21 22
)
for E
(
E E
11

A
1
s
1
)
=
.
1
6
|
111+
(

1
2
)

1
2
)
1+
(

1
2
)

1
2
)
1+111+
(

1
2
)

1
2
)
1+
(

1
2
)

1
2
)
1

.
111+
(

1
2
)

1
2
)
1+
(

1
2
)

1
2
)
1+111+
(

1
2
)

1
2
)
1+
(

1
2
)

1
2
)
1
=
.
1
6
|
1+
1
4
+
1
4
+1+
1
4
+
1
4

.
1+
1
4
+
1
4
+1+
1
4
+
1
4
=
.
1
6
3
.3
=
.
1
23
3
.3
=
1
.2
(
E E
22

A
1
s
1
)
=
.
1
6
|
111+
(

1
2
)

1
2
)
1+
(

1
2
)

1
2
)
1+111+
(
1
2
)

(
1
2
)
1+
(
1
2
)

(
1
2
)
1

.
111+
(

1
2
)

1
2
)
1+
(

1
2
)

1
2
)
1+111+
(
1
2
)

(
1
2
)
1+
(
1
2
)

(
1
2
)
1
=
.
1
6
|
1+
1
4
+
1
4
+1+
1
4
+
1
4

.
1+
1
4
+
1
4
+1+
1
4
+
1
4
=
.
1
6
3
.3
=
.
1
23
3
.3
=
1
.2
(
E E
12

A
1
s
1
)
=
.
l

h

R=1
6
I
12
( E)
( R) I
21
( E)
( R) I
11
( A
1
)
( R)
.

R=1
6
I
22
( E)
( R)I
11
( E)
( R) I
11
( A
1
)
( R)
(
E E
12

A
1
s
1
)
=
.
1
6
|
001+
(
.3
2
)

.3
2
)
1+
(

.3
2
)

(
.3
2
)
1+001+
(

.3
2
)

.3
2
)
1+
(
.3
2
)

(
.3
2
)
1

.
111+
(

1
2
)

1
2
)
1+
(

1
2
)

1
2
)
1+11(1)+
(
1
2
)

1
2
)
1+
(
1
2
)

1
2
)
1
=
.
1
6
|

3
4

3
4
+
3
4
+
3
4

.
1+
1
4
+
1
4
1
1
4

1
4
=
0
0
we have
0
0
and in this case we use the formula (4.15.13)
45
(
E E
12

A
1
s
1
)(
E E
21

A
1
s
1
)

=
.
1
6
|
001+
(
.3
2
)

.3
2
)
1+
(

.3
2
)

(
.3
2
)
1+001+
(

.3
2
)

.3
2
)
1+
(
.3
2
)

(
.3
2
)
1

=
.
1
6
|

3
4

3
4
+
3
4
+
3
4

=0
Thus we get:
(
E E
i k

A
1
1
)
=
1
.2
(
1 0
0 1
)
(4.15.16)
for
A
2
See pag 85[70] we take i= j , k=l , m=n in (4.15.13) and obtain at least one CGC which is
different from zero, then we keep j , l , n constant and vary i , k , m :
(
E E
11

A
2
s
1
)
=
.
111+
(

1
2
)

1
2
)
1+
(

1
2
)

1
2
)
1+11(1)+
(

1
2
)

1
2
)
(1)+
(

1
2
)

1
2
)
(1)
=
.
1+
1
4
+
1
4
1
1
4

1
4
=0
thus tis square root is not good.
(
E E
12

A
2
s
1
)
=
.
l

R=1
6
I
12
( E)
( R) I
21
( E)
( R)I
11
( A
1
)
( R)
.

R=1
6
I
22
( E)
( R) I
11
( E)
( R) I
11
(A
1
)
( R)
(4.15.17)
46
(
E E
12

A
2
s
1
)
=
(
E E
21

A
2
s
1
)
=
.
1
6
|
001+
(
.3
2
)

.3
2
)
1+
(

.3
2
)

(
.3
2
)
1+001+
(

.3
2
)

.3
2
)
(1)+
(
.3
2
)

(
.3
2
)
(1)

.
111+
(

1
2
)

1
2
)
1+
(

1
2
)

1
2
)
1+111+
(
1
2
)

1
2
)
(1)+
(
1
2
)

1
2
)
(1)
=
.
1
6
|

3
4

3
4

3
4

3
4

.
1+
1
4
+
1
4
+1+
1
4
+
1
4
=
.
1
6
3
.3
=
.
1
23
3
.3
=
1
. 2
Thus we find a sure root different from zero and we fiw j =2,l =1, n=1 thus
(
E E
x y

A
2
s
1
)
=
.
l

R=1
6
I
x2
( E)
( R) I
y1
( E)
( R)I
11
( A
1
)
( R)
.

R=1
6
I
22
( E)
( R) I
11
( E)
( R) I
11
(A
1
)
( R)
(4.15.18)
xy=11 From (4.15.18) :
(
E E
11

A
2
s
1
)
=
.
1
6
|
011+
(
.3
2
)

1
2
)
1+
(

.3
2
)

1
2
)
1+011+
(

.3
2
)

1
2
)
(1)+
(
.3
2
)

1
2
)
(1)

.
111+
(

1
2
)

1
2
)
1+
(

1
2
)

1
2
)
1+111+
(
1
2
)

1
2
)
(1)+
(
1
2
)

1
2
)
(1)
=0
xy=22 From (4.15.18) we get:
(
E E
22

A
2
s
1
)
=0
xy=21 From (4.15.18) we get:
47
(
E E
21

A
2
s
1
)
=
.
1
6
|
111+
(

1
2
)

1
2
)
1+
(

1
2
)

1
2
)
1+111+
(
1
2
)

1
2
)
(1)+
(
1
2
)

1
2
)
(1)

.
111+
(

1
2
)

1
2
)
1+
(

1
2
)

1
2
)
1+111+
(
1
2
)

1
2
)
(1)+
(
1
2
)

1
2
)
(1)
=
.
1
6
|
1+
1
4
+
1
4
+1+
1
4
+
1
4

.
1+
1
4
+
1
4
+1+
1
4
+
1
4
=
.
1
6
3
.3
=
.
1
23
3
.3
=
1
.2
thus we get again:
(
E E
i k

A
1
1
)
=
1
.2
(
0 1
1 0
)
(4.15.19)
The same procedure for E
l

=2
this is the dimension of E 2x2 matrix:
(
E E
i k

E
2
)
=
1
.2
(
0 1
1 0
)

(
E E
i k

E
1
)
=
1
.2
(
1 0
0 1
)
(4.15.20)
If
f
1
,
f
2
and
g
1
,
g
2
are basis functions belonging to I
( E)
, then basis functions in
I
( EE)
(
EE=A
1
A
2
E
)are from (4.15.5):

( A
1
)
=
1
.2
( f
1
g
1
+ f
2
g
2
)
( A
2
)
=
1
.2
( f
1
g
2
f
2
g
1
)

1
( E)
=
1
.2
( f
1
g
2
+ f
2
g
1
)
2
( E)
=
1
.2
( f
1
g
1
f
2
g
2
) 53
(4.15.21)
Or if you want
f
1
, f
2
=
1
E
(1) ,
2
E
(1) and g
1
, g
2
=
1
E
(2) ,
2
E
(2) (4.15.22)
You can see eq (11) and (12a,b,c,d) from [1], actually he solve the problem 4.11 at pag 86 using table
8.1 pag 196 from [70]. Where problem 4.11 from [70] is another way for finding CGC by applying
projector operators (4.11.5) to (4.15.22).where CGC are from (4.15.5) after ortho-normalization. This
procedure you can also see in[77] pag 47,48.
48
At pag 85[70] is not correct see pag 287 Sugano [77].

A
1
A
2
E E
u v
u
1
.2
0
1
.2
0
v 0
1
.2
0
1
.2
u 0
1
.2
0
1
.2
v
1
.2
0
1
.2
0
C
EE
=
(
1
.2
0
1
.2
0
0
1
.2
0
1
.2
0
1
.2
0
1
.2
1
.2
0
1
.2
0
)
(4.15.23)
Therefore (4.15.23) Is a unitary matrix(you can verify by applying eq. (4.5.3) ).
Finally you can verify that:
(C
EE
)
1
I
( EE)
C
EE
=I
A
1
I
A
2
I
E
(4.15.24)
4.16 Full matrix representations
We list here full matrix representations for several groups. Abelian groups are omitted, as their irreps
are one-dimensional and hence all the necessary information is contained in the character table. We
give C3v (isomorphic with D3) and C4v (isomorphic with D4 and D2d). By employing higher l value
spherical harmonics as basis functions it is straightforward to extend these to Cnv for any n, even or
49
odd. We note that the even n Cnv case has four nondegenerate irreps while the odd n Cnv case has only
two.
Table 1.3
C
3v
and
D
3
Matrix irreducible representations:
D
3
E C
3 C
3
2
C
2
a
C
2
b
C
2
c
C
3v
E C
3 C
3
2
c
v
a
c
v
b
c
v
c
A
1
A
1
1 1 1 1 1 1
A
2
A
2
1 1 1 -1 -1 -1
( E)
11
( E)
11
1

1
2

1
2
1

1
2

1
2
( E)
21
( E)
21
0
.3
2

.3
2
0

.3
2
.3
2
( E)
12
( E)
12
0

.3
2
.3
2
0

.3
2
.3
2
( E)
22
( E)
22
1

1
2

1
2
-1 1
2
1
2
50
Table 1.4
D
4
,
D
2d
and
D
4v
Matrix irreducible representations:
D
4
E
C
2

C
4
C
4
3
C
2
x
C
2
y
C
2
135
C
2
45
D
2d
E
C
2

S
4
S
4
3
C
2
x
C
2
y
C
2
135
c
2
45
D
4v
E
C
2

C
4
C
4
3
c
xz
c
yz
c
2
45
c
2
135
A
1
A
2
B
1
B
2
( E)
11
( E)
21
( E)
12
( E)
22
A
1
A
2
B
1
B
2
( E)
11
( E)
21
( E)
12
( E)
22
A
1
A
2
B
1
B
2
( E)
11
( E)
21
( E)
12
( E)
22
1 1 1 1 1 1 1 1 I
1

1 1 1 1 -1 -1 -1 -1 I
2
1 1 -1 -1 1 1 -1 -1 I
3
1 1 -1 -1 -1 -1 1 1 I
4
1 -1 0 0 1 -1 0 0 I
5
0 0 1 -1 0 0 1 -1 I
5
0 0 -1 1 0 0 -1 1 I
5
1 -1 0 0 -1 1 0 0 I
5

The numbers 45 and 135 refer to the angles (in degrees) the particular axis makes with the positive x
axis, or the plane makes with the xz plane.
Clebsch-Gordan coefficients for the crystallographic point group
D
4
See pag 76-77 [78] :
Using the matrices of the two-dimensional irreducible representation I
5
specified in Table 1.4 , the
Clebsch-Gordan coefficients corresponding to the series I
5
I
4
I
5
are given by Equation
(4.15.15) (with j =2,l =1, n=2 ) as
(
54
11

51
2
)
=
(
54
21

51
1
)
=1
(
54
11

51
1
)
=
(
54
21

51
2
)
=0
Similarly for I
5
I
3
I
5
(with j =2,l =1, n=2 )
(
53
11

51
2
)
=
(
53
21

51
1
)
=1
(
53
11

51
1
)
=
(
53
21

51
2
)
=0
Likewise for I
5
I
5
I
1
I
2
I
3
I
4
.Equation (4.15.15) implies that all the Clebsch-Gordan
51
coefficients are zero except the following:
(
55
11

11
1
)
=
(
55
22

11
1
)
=
1
.2
(
55
11

21
1
)
=
(
55
22

21
1
)
=
1
.2
(
55
21

31
1
)
=
(
55
12

31
1
)
=
1
.2
(
55
21

41
1
)
=
(
55
12

41
1
)
=
1
.2
4.17 Selections rules
See pag 109 [71] :
when calculating various matrix elements in quantum mechanics some of them happen to vanish for
reason of symmetry. Representation theory greatly helps in judjing whether or not a given matrix
element vanishes by symmetry.
Let us examine a matrix element like
(
m
(o)
, H
l
( )
) (4.17.1)
Where H is the hamiltonian or any other operator that is invariant under the symmetry group G .
Invariance of H means that H
l
()
transform in exactly the same way as
l
( )
. then the
orthogonality relation
(
m
(o)
,
l
( )
)=6
o
6
ml
constant independent of m and l (4.17.2)
Indicates that the above matrix element is non-vanishing only when o= and m=l and that it is
independent of m. That is, the Hamiltonian has non-vanishing matrix elements only between the
functions that have the same transformations properties.
To consider matrix elements of general operators it is convenient to define irreducible tensor operators.
In parallel with the basis functions
m
( o)
transforming like
R
m
(o)
=

m'

m'
( o)
I
m'
(o)
( R)
(4.17.3)
The operators T
m
(o)
which transform like
RT
m
(o)
R
1
=

m'
T
m'
(o)
I
m'
( o)
( R)
(4.17.4)
Are called irreducible tensors operators. For instance in the group
C
3v
components of the vector r
, momentum p and angular momentum l vectors constitute irreducible tensor operators
belonging to the following irreducible representations:
52
A
1
: z ,
p
z
A
2
:
l
z
E : x , y ,
p
x
, p
y

,
l
x
, l
y

.
Whether or not a matrix element of the irreducible tensor operator T
j
(o)
(
m
( )
, T
j
(o)

l
( )
) (4.17.5)
vanishes by symmetry is examined in the following way. The functions T
j
(o)

l
( )
transform as basis
functions of the product representation I
(o)
I
( )
. So the function T
j
(o)

l
( )
contains in itself
irreducible components that are obtained by reduction of the product representation I
(o)
I
( )
. In
order that the matrix element (4.17.5) should not vanish by symmetry it has to contain the
m
( )
component because of the orthogonality relation (4.17.2). This requires that the representation I
( )
should appear at least once in the reduction of the product representation I
(o)
I
( )
Product representations are reducible in general . If I
(o)
I
( )
has the irreducible decomposition
I
(o)
I
( )
=

I
( )
(4.17.6)
Then the values of
q

may be calculated by means of

q

=
1
g

G
X
( )
(G)

X
(o)
(G)=
1
g

G
X
( )
(G)

X
( o)
(G)X
( )
(G)
(4.17.7)
Here q

gives the number of the times the representation I

( )
apears in the reduction of
I
(o)
I
( )
.
Thus the matrix element vanishes by symmetry if q

=0 .
see pag 67 [71] is equivalent with (4.15.21):
As an example let us examine the selection rules for photoabsorbtion by an atom placed in a field of
C
3v
symmetry. Interaction of the electron with light has the form pe , where e stands for the
polarisation of the electric field . Suppose that the initial state belongs to the irreducible representation
I
i
. For light polarised in the z direction the optical transition takes place trough
p
z
.Since the
operator
p
z
belongs to
A
1
representation of
C
3v
the final state must be
A
1
I
i
=I
i
. So
p
z
causes transitions between states with the same symmetry.
When the light is polarized in the xy-plane the transitions takes place trough
p
x
and
p
y
wich
belong to the representation E . The symmetry of final states is obtained by reducing
EI
i
. The
result of this reduction turns out to be
E , E , A
1
A
2
E
for
I
i
=A
1,
A
2,
E
.
4.18 (SO
3
)Linear combinations of spherical harmonics of point
groups
See pag 88 [70] :
For the point groups that are subgroups of
SO
3
we obtain the standard REPs via the spherical
harmonics Y
m
l
. These Y
m
l
are the basis functions of the Irs I
(l )
of the rotation group
SO
3
and
constitute a generally reducible basis for REPs of point groups.
The spherical harmonics ( 0 , : angles of spherical polar coordinates)
53
Y
m
l
(0, )=
1
.2n
0
m
l
()e
i m
, m0
56 (4.18.1)
0
m
l
()=
(
2l +1
2
( lm) !
(l +m) !
)
1
2 (1)
m
2
l
l !
sin
m

(

cos
)
l +m
(cos
2
1)
l
Y
m
l
=(1)
m
Y
m
l
, l ml
constitute a 2l +1 dimensional linear space for the REPs of point groups.
Often it is useful to chose real functions, thus (m0)
Y
m, c
l
=
1
.2
|
(1)
m
Y
m
l
+Y
m
l

=(1)
m 1
.n
0
m
l
cosm
Y
m, s
l
=
i
.2
|
(1)
m
Y
m
l
Y
m
l

=(1)
m 1
.n
0
m
l
sinm

(4.18.2)
For those point groups with one main axis thee real functions are bases for the standard REPs . In the
case of cubic point groups we have to chose linear combinations of spherical harmonics adptet to the
cubic symmetry: the cubic harmonics are different from real spherical harmonics for l 3 . The
spherical harmonics are denoted as s-, p-, d-, f-, , or more detailed
p
x
,
p
y
,..., according to their
use in quantum mechanics see the Table 1.5:
54
Table 1.5 Linear combinations of spherical harmonics of point groups according to (4.18.1),(4.18.2)
for l =0 to l =3 pag 88 [70]:
Y
m
l
Normalization Spherical coordinates Cartesian coordinates
Y
0
0
s
.1/ 4n 1 1
Y
0
1
Y
1c
1
Y
1 s
1
p
z
p
x
p
y
.3/ 4n
.3/ 4n
.3/ 4n
cos
sin cos
sinsin
z
x
y
Y
0
2
Y
1c
2
Y
1 s
2
Y
2c
2
Y
2s
2
d
0
d
1c
d
1s
d
2c
d
2s
.5/ 16n
.15/ 4n
.15/ 4n
.15/ 16n
.15/ 16n
3cos
2
1
sincos cos
sincos sin
sin
2
cos2
sin
2
sin 2
3z
2
1=2z
2
x
2
y
2
zx
zy
x
2
y
2
2 xy
Y
0
3
Y
1c
3
Y
1 s
3
f
0
f
1c
f
1s
.7/ 16n
.21/ 32n
.21/ 32n
cos (5cos
2
3)
sin(5cos
2
1)cos
sin(5cos
2
1)sin
z (5z
2
3)=z(2z
2
3x
2
3y
2
)
x(5z
2
1)=x(4z
2
x
2
y
2
)
y(5z
2
1)=y( 4z
2
x
2
y
2
)
Y
2c
3
Y
2s
3
Y
3c
3
Y
3 s
3
f
2c
f
2s
f
3c
f
3s
.105/ 16n
.105/ 16n
.35/ 32n
.35/ 32n
sin
2
coscos 2
sin
2
cossin 2
sin
3
cos 3
sin
3
sin3
z ( x
2
y
2
)
2 xyz
x( x
2
3y
2
)
y(3 x
2
y
2
)
This is equivalent with
Table 1.6 Character table of
C
3v
with assigned functions
E 2C
3
3c
v
s p d L
I
(1)
A
1
I
( 2)
A
2
I
(3)
E
1
1
2
1
1
-1
1
-1
0
1 z
( x , y)
z
2
: singlets
doublets:
(2 xy , x
2
y
2
) ; ( xz , yz)
L
z
L
x
, L
y
The spherical harmonics see pag 3 [69]:
55
Y
l m
(0, )=.(1)
m+m
(
2l +1
2
(l m) !
(l +m) !
)
1
2
P
l
m
(cos0) e
i m
=(4.18.1) (4.18.3)
Table 1.7 Spherical harmonics
l m
r
l
Y
l m
( x , y , z)
Y
l m
(0, )
0
1
1
2
2
2
3
3
3
3
0
0
!1
0
!1
!2
0
!1
!2
!3
.
1
4n
.
3
4n
z

.
3
8n
( x!i y)
.
5
4n.
1
4
(3z
2
r
2
)

.
5
4n.
3
2
z( x!i y)
.
5
4n.
3
8
( x!i y)
2
.
7
4n.
1
4
z (5z
2
3r
2
)

.
7
4n.
3
16
( x!i y)(5z
2
3r
2
)
.
7
4n.
15
8
z( x!i y)
2

.
7
4n.
15
16
( x!i y)
3
.
1
4n
.
3
4n
cos 0

.
3
8n
sin 0e
!i
.
5
4n.
1
4
(3cos
2
1)

.
5
4n.
3
2
cos0sin 0e
!i
.
5
4n.
3
2
sin
2
0e
!2i
.
7
4n.
1
4
(2cos
3
03cos 0sin
2
0)
.
7
4n.
3
16
( 4cos
2
0sin0sin
3
0)e
!i
.
7
4n.
15
8
cos0sin
2
0e
!2i

.
7
4n.
15
16
sin
3
0e
!3i
Proof:
x=r sin cos y=rsin sin z=r cos
Y
2,!2
=
.
5
4n.
3
8
( x!i y)
2
=
.
5
4n.
3
8
(cos
2
+2i sincossin
2
) r
2
sin
2
0
=
.
5
4n.
3
8
e
!2i
r
2
sin
2
0
(4.18.4)
56
Table 1.8 Linear combinations of spherical harmonics = pag 6 [69]:=pag 178 [79]:
Spherical harmonics Spherical coordinates Cartesian coordinates
s
.4nY
00
1 1
p
z
p
x
p
y
.
4n
3
Y
10
r
.
4n
3 .
1
2
(Y
11
+Y
11
) r
.
4n
3 .
1
2
i ( Y
11
+Y
11
) r
r cos
r sincos
r sinsin
z
x
y
d
z
2
d
x
2
y
2
d
xy
d
yz
d
zx
.
4n
5
Y
20
r
2
.
4n
5 .
1
2
( Y
22
+Y
22
) r
2
.
4n
5 .
1
2
i (Y
22
+Y
22
) r
2
.
4n
5 .
1
2
i ( Y
21
+Y
21
) r
2
.
4n
5 .
1
2
(Y
21
+Y
21
) r
2
1
2
r
2
(3cos
2
1)
1
2
.3r
2
sin
2
cos 2
1
2
.3r
2
sin
2
sin2
.3r
2
sin coscos
.3r
2
sincossin
1
2
(3z
2
r
2
)
1
2
.3( x
2
y
2
)
.3 xy
.3 yz
.3 zx
Proof:
take into account that
e
2i
=cos 2+i sin 2 (4.18.5)
And using the formula (4.18.4) we get:
.
4n
5 .
1
2
( Y
22
+Y
22
) r
2
=
1
2
.3r
2
sin
2
cos 2 (4.18.6)
Table From Table 1.8 we see the formula from pag 30 [28]:
r sin cos=
.
4n
3 .
1
2
(Y
11
+Y
11
) r (4.18.7)
57

Chapter 5 Tensors
5.1 Direct products, vectors
pag 11 [11]
Direct products
The direct product of two matrices (given the symbol ) is a special type of matrix product that generates
a matrix of higher dimensionality if both matrices have dimension greater than one. The easiest way to
demonstrate how to construct a direct product of two matrices A and B is by an example:
58
AB=
(
a
11
a
12
a
21
a
22
)

(
b
11
b
12
b
21
b
22
)
=
(
a
11
B a
12
B
a
21
B a
22
B
)
=
=
(
a
11
b
11
a
11
b
12
a
12
b
11
a
12
b
12
a
11
b
21
a
11
b
22
a
12
b
21
a
12
b
22
a
21
b
11
a
21
b
12
a
22
b
11
a
22
b
12
a
21
b
21
a
21
b
22
a
22
b
21
a
22
b
22
)
Though this may seem like a somewhat strange operation to carry out, direct products crop up a great
deal in group theory.
Pag 390 [17]
The third kind of multiplication of two vectors A and B is the direct product which is represented by
AB. It is defined by writing each vector in terms of its components using eq. (A8.3.6) and forming the
nine possible products of pairs of components by ordinary multiplication. Thus
A=A
x
e
x
+A
y
e
y
+A
z
e
z
(A. 8.3.6)
AB=( e
x
A
x
+e
y
A
y
+e
z
A
z
)(e
x
B
x
+e
y
B
y
+e
z
B
z
)=
=A
x
B
x
e
x
e
x
+A
x
B
y
e
x
e
y
+A
x
B
z
e
x
e
z
+A
y
B
x
e
y
e
x
+A
y
B
y
e
y
e
y
+
+A
y
B
z
e
y
e
z
+A
z
B
x
e
z
e
x
+A
z
B
y
e
z
e
y
+A
z
B
z
e
z
e
z
(A 8.5.20)
pag 417 [17]
The direct product AB of two vectors A and B which is defined in Chapter A8 constitutes a
second-rank tensor. We shall denote this generally by T
2
where the superscript 2 denotes the
rank. Thus
T
2
= AB
This tensor is said to be of rank two because each of the nine terms in the expansion of AB in eq.
(A8.5.20) involves dyads (bivalent , cate doi) which are the products of two vector components. We
may say that T
2
is a dyad which can be expressed as a dyadic, i.e. a sum of dyads. The tensor
T
2
is a linear operator which sends a vector V into another vector according to the following
rule:
T
2
(V )=ABC(V )=AB(CV )
The result is clearly a second-rank tensor as the direct product AB is a second-rank tensor and
CV is a scalar. T
3
can also act as a linear operator on a vector dyad VW and produce a
vector according to the rule
T
3
(VW )=ABC( VW)=ABC: VW=A( CV )( BW ) (A10.1.6)
The result is a vector, because A is a vector and CV and BW are scalars. Finally, T
3
can
act as a linear operator on a vector triad VWX and produce a scalar according to the rule
T
3
(VWX )=ABC(VWX )=ABCVWX=(CV )( BW)( AX )
59
The result is clearly a scalar because all terms in the last line are scalars. The symbol is termed a
triple dot product and the process may be described as the triple dot product of a triad acting on a triad.
Pag 420 [17]
We may represent a second rank tensor T
2
by the following 33 matrix of this nine dyad
components:
T
2

|
T
xx
T
xy
T
xz
T
yx
T
yy
T
yz
T
zy
T
zy
T
zz

(A10.2.1)
where
T
xx
=A
x
B
x
, T
xy
=A
x
B
y
etc. in accordance with eq. (A8.5.20). This representation has as its
basis the nine pairs of cartesian basis vectors, or dyads. We can see that the linear operation of T
2

on a vector V defined in eq. (A10.1.2) may now be expressed in the form of a matrix equation:
|
V
x
'
V
y
'
V
z
'
=
|
T
xx
T
xy
T
xz
T
yx
T
yy
T
yz
T
zy
T
zy
T
zz
|
V
x
V
y
V
z

(A10.2.2)
where
V
x
, V
y
, V
z
are the components of the original vector V and V
x
'
, V
y
'
, V
z
'
are the
components of the transformed vector V
'
. Both sets of components are related to the same cartesian
axis system, namely x, y, z.
It is often convenient to use the compact matrix form for eq. (A10.2.2) and write
V
'
=T
2
V (A10.2.3)
Equation (A10.2.2) is equivalent to the following set of three linear equations:
V
x
'
=T
xx
V
x
+T
xy
V
y
+T
xz
V
z
V
y
'
=T
yx
V
x
+T
yy
V
y
+T
yz
V
z
V
z
'
=T
zx
V
x
+T
zy
V
y
+T
zz
V
z
(A10.2.4)
In the definition of T
2
given by eq. (A10.1.2) the selection of the appropriate products of pairs of
components of B and V is made by following the rules of scalar product formation. In the
matrix representation the corresponding process is performed by following the rules of matrix
multiplication. These rules involve matching the second subscripts of a component of T having first
subscripts x, with the same subscript of a component of V and then summing over all possible
values x, y, z of these second subscripts of T
2
to give V
x
'
and so on. The selection process is
readily seen if the set of eqs. (A10.2.4) is written in the summation nomenclature,
V
j
'
=T
jc
V
c

j=x , y , z
c=x , y , z
(A10.2.5)
Equation (A10.2.5) is yet another method of representing eq. (A10.2.2). Likewise, we may represent a
third-rank tensor T
3
by a 39 matrix of its 27 components
T
3
=
|
T
xxx
T
xyy
T
xzz
T
xxy
T
xyx
T
xyz
T
xzy
T
xzx
T
xxz
T
yxx
T
yyy
T
yzz
T
yxy
T
yyx
T
yyz
T
yzy
T
yzx
T
yxz
T
zxx
T
zyy
T
zzz
T
zxy
T
zyx
T
zyz
T
zzy
T
zzx
T
zxz

(A10.2.6)
60
This representation has as its basis the 27 triads of cartesian basis vectors etc. The linear operation of
T
3
on a vector dyad, defined in eq. (A10.1.6) may then be expressed in the form of a matrix
equation
|
V
x
'
V
y
'
V
z
'
=T
3
=
|
T
xxx
T
xyy
T
xzz
T
xxy
T
xyx
T
xyz
T
xzy
T
xzx
T
xxz
T
yxx
T
yyy
T
yzz
T
yxy
T
yyx
T
yyz
T
yzy
T
yzx
T
yxz
T
zxx
T
zyy
T
zzz
T
zxy
T
zyx
T
zyz
T
zzy
T
zzx
T
zxz

|
V
x
W
x
V
y
W
x
V
z
W
z
V
x
W
x
V
y
W
x
V
z
W
z
V
x
W
x
V
y
W
x
V
z
W
z

(A10.2.7)
where we have used a column matrix of nine rows to represent the components of the vector dyad. The
set of three linear equations for V
x
'
, V
y
'
, V
z
'
follow readily from eq. (A10.2.7). The compact form of
eq. (A10.2.7) is
V
'
=T
3
(VW ) (A 10.2.8)
or equivalently
V
'
=ABC : VW (A 10.2.9)
Comparison of eq. (A10.2.9) with eq. (A8.6.10) which gives the 27 cartesian-based components of the
direct product of three vectors ABC shows how the subscripts on the 27 terms
T
xyz
, T
xyy
, ...
etc
arise.
Equation (A10.2.7) may be rewritten using the summation convention
V
j '
'
=T
jct
V
c
W
t

j=x , y , z
c=x , y , z
t=x , y , z
(A 10.2.10)
IRREDUCIBLE TENSORIAL SETS
We begin by defining a tensorial set. A tensorial set is the set of all the components of a tensor, and we
shall represent these as a column matrix. For a first-rank tensor T
1
, this column matrix has three
entries; for a second-rank tensor T
2
it has nine entries; and for a tensor of rank R it has 3R entries.
For the special case of a first-rank tensor, the tensorial set of three components corresponds to the set of
three components of a vector. Under a rotational transformation (rotation of coordinate axes), a
tensorial set a with components
a
i
transforms to a new set b with components
b
k
. The
b
k

are related to the ai as follows:
b
k
=

i
D
ki
a
i
(A 10.5.1)
where the
D
ki
are transformation coefficients. In general, each
b
k
is a linear combination of all
the
a
i
. The relationship between the tensorial sets b and a may also be expressed in compact matrix
61
form as
b=Da (A 10.5.2)
where D is a 3
R
3
R
matrix of the transformation coefficients
D
ki
, and R is the rank of
the tensor. D is required to have an inverse, that is det D0 . However, it is often possible to
replace the tensorial set a by a new set a
'
, such that a rotational transformation transforms
certain subsets of a
'
separately. The components of the new set a
'
are related to the components
of the old set a by a unitary transformation,
a
r '
=

A
ri
a
i
(A 10.5.3)
where the Ari are coefficients. The corresponding
compact matrix equation is
a' =Aa
(A 10.5.4)
where A is a 3
R
3
R
matrix of the coefficients
A
ri
. It then follows that the rotational transformation
of the new tensorial set a' is given, in compact
matrix notation, by
b
'
=D
'
a
'
(A 10.5.5)
where
D' =ADA
1
The transformation matrix D' has its non-vanishing
elements concentrated in square blocks or sub-matrices
along the diagonal (see Fig. A10.1). Each of the subsets
constitutes a separate tensorial set whose transformation
matrix is one of the submatrices along the diagonal of
D'
.
Consider first the simultaneous reduction of the set of components of an ordinary tensor T and of
the corresponding set of unit basis tensors. This operation splits the tensor into a sum of tensors, each
of which consists of an irreducible set of components and of an irreducible set of basis tensors. Each of
these tensors may accordingly be called an irreducible tensor. For example, a second-rank tensor
represented by
T=e
x
e
x
T
xx
+e
x
e
y
T
xy
+...+e
z
e
z
T
zz
(A 10.5.7)
resolves into three irreducible parts,
T=T
( 0)
+T
( 1)
+T
(2)
(A 10.5.8)
where
T
( 0)
=
1
3
(e
x
e
x
+e
y
e
y
+e
z
e
z
)(T
xx
+T
yy
+T
zz
)
(A 10.5.9)
T
(1)
=
1
2
|( e
y
e
z
e
z
e
y
)(T
yz
T
zy
)+(e
z
e
x
e
x
e
z
)(T
zx
T
xz
)+(e
x
e
y
e
y
e
x
)(T
xy
T
yx
)
(A 10.5.10)
T
( 2)
=
1
2
|
1
3
(2e
z
e
z
e
x
e
x
e
y
e
y
)( 2T
zz
T
xx
+T
yy
)+
62
Fig. A10.1: Diagrammatic representation of a
transformation matrix in reduced form. All
matrices outside the shaded areas vanish.
+(e
x
e
x
e
y
e
y
)(T
xx
T
yy
)+(e
y
e
z
+e
z
e
y
)(T
yz
T
zy
)+(e
z
e
x
+e
x
e
z
)(T
zx
T
xz
)
(A 10.5.11)
and the superscripts in parentheses label irreducible representations and not rank.
Alternatives to the word rank sometimes used in the literature are degree and order. Alternatives to
tensor are names which incorporate the rank as for example: diad, triad, tetrad; or bisor, trisor, tetror.
These have not found much favour.
The superscript for rank is placed in braces f g to avoid confusion with the labels for irreducible
tensor components which are written in parentheses ( ) as e.g. T
( 0)
. In many situations the tensor
rank symbol can be omitted without creating ambiguities.
The five equations above need careful study. Equations (A10.5.9) to (A10.5.11) emphasize the
structures of T
( 0)
, T
(1)
and T
( 2)
in terms of irreducible basis sets. However, T
( 0)
, T
(1)

and T
( 2)
may also be written out in the form given by eq. (A10.5.7) giving essentially vector
representations. In this sense they may each be regarded as tensors of second rank with non-
independent components.
Consider first T
( 0)
. We see from eq. (A10.5.9) that it is the product of two quantities
1/ .3(e
x
e
x
+e
y
e
y
+e
z
e
z
) : which involves dyads of basis vectors; and 1/ .3(T
xx
+T
yy
+T
zz
)
which involves components of the basis vector dyads. Each of these is invariant under a unitary
rotation transformation and so is a scalar. Thus T
( 0)
is a scalar or a zero rank tensor. However, if we
introduce a quantity a given by
a=
1
3
(T
xx
+T
yy
+T
zz
)
(A 10.5.12) (5.1.1)
then (A10.5.9) can also be written as
T
( 0)
=e
x
e
x
a+e
y
e
y
a+e
z
e
z
a+e
x
e
y
0+... (A 10.5.13)
using the form defined by eq. (A10.5.7) We see that this corresponds to a second-rank tensor of a
particular type, namely an isotropic tensor. It has only three non-zero components which are associated
with
e
x
e
x
, e
y
e
y
, e
z
e
z
and each component is equal to a. The matrix representation of the
components is
T
0

|
a 0 0
0 a 0
0 0 a

(A 10.5.14)
We consider now eq. (A 10.5.10) for T
(1)
. We see that T
(1)
is a vector with components
1/ .2(T
yz
T
zy
) , 1/ .2(T
zx
T
xz
) and 1/ .2(T
xy
T
yx
) and three basis vectors
1/ .2(e
y
e
z
e
z
e
y
) , 1/ .2(e
z
e
x
e
x
e
z
) and 1/ .2(e
x
e
y
e
y
e
x
) . it is also a tensor of rank of
unit rank. Equation (A 10.5.10) can be also written as
T
(1)
=e
x
e
x
0+e
y
e
y
0+e
z
e
z
0+
+e
x
e
y
1
2
(T
xy
T
yx
)+e
y
e
x
1
2
(T
yx
T
xy
)
63
+e
y
e
z
1
2
(T
yz
T
zy
)+e
z
e
y
1
2
(T
zy
T
yz
)
+e
z
e
x
1
2
(T
zx
T
xz
)+e
x
e
z
1
2
(T
xz
T
zx
)
(A 10.5.15)
using the form defined by (A10.5.7). This corresponds to an antisymmetric second-rank tensor. The
matrix representation of the components is
T
1

|
0
1
2
(T
xy
T
yx
)
1
2
(T
xz
T
zx
)
1
2
(T
yx
T
xy
) 0
1
2
(T
yz
T
zy
)
1
2
(T
zx
T
xz
)
1
2
(T
zy
T
yz
) 0

(A 10.5.16)
Finally we consider eq. (A10.5.11) for T
( 2)
which involves five components and five basis vectors.
For example 1/ .6( 2T
zz
T
xx
+T
yy
) is the component associated with the basis vector
1/ .6( 2e
z
e
z
e
x
e
x
e
y
e
y
) and so on. The five basis vectors 1/ .6( 2e
z
e
z
e
x
e
x
e
y
e
y
) ,
1/ .2(e
x
e
x
e
y
e
y
) . . . constitute the simplest set of irreducible unit basis vectors of order five. We
may also represent T
( 2)
using the form defined by eq. (A10.5.7):
T
(1)
=e
x
e
x
(T
xx
a)+e
y
e
y
(T
yy
a)+e
z
e
z
(T
zz
a)+
+e
x
e
y
1
2
(T
xy
T
yx
)+e
y
e
x
1
2
(T
yx
T
xy
)
+e
y
e
z
1
2
(T
yz
T
zy
)+e
z
e
y
1
2
(T
zy
T
yz
)
+e
z
e
x
1
2
(T
zx
T
xz
)+e
x
e
z
1
2
(T
xz
T
zx
)
(A 10.5.17)
This constitutes yet another type of second-rank tensor, a symmetric traceless tensor. Its matrix
representation is
T
1

|
T
xx
a
1
2
(T
xy
T
yx
)
1
2
(T
xz
T
zx
)
1
2
(T
yx
T
xy
) T
yy
a
1
2
(T
yz
T
zy
)
1
2
(T
zx
T
xz
)
1
2
(T
zy
T
yz
) T
zz
a

(A 10.5.18)
pag 159 [25]
64
so you can see Wolkenstein (bond polarizability tensors )or pag 23-25[21].
see Feynman V II, p 390 (31-1 to 31-7) [27].
What is most important that if you remember the experiments that you have done Chetrus's labs , so
you have a parallelepiped [,pr,l l pap d] if you will chose the system of coordinates that do not
coincide with principal axes so you will get a tensor with non diagonal components different from zero.
Or for different objects you can chose one bases that coincide with principles axes so you will have the
tensor with non diagonal components zero or that is the same you have only the diagonal components.
In other context by rotations(diagonalization) you can reduce to the diagonal components only.
In other problems you find a basis (that is a set of vectors or functions e.g. Cartesian basis or orbitals)
that their matrices or tensor is already diagonalized.
So this is the main task of quantum mechanics. To find a complete set. Or to represent the operators in
such basis that is easy to deal with them e.g. eigenfunctions.
65
5.2 Tensor continuation Polarizability Directions cosines
pag 343 [17]
We shall refer to an axis system fixed at the center of the nuclear mass of a molecule, and parallel to the
laboratory axis system as a space-fixed system and an axis system fixed in the nuclear frame-work,
so that it rotates with the molecule as a molecule-fixed system.
pag 172 [18]
The electric polarizability o of a molecule is a tensor since it relates the induced electric dipole
moment vector to the applied electric field vector through
j=o E (4.2.6)
The directions of the influence E and the response j are not necessarily the same on account of
anisotropy in the electrical properties of the molecule. If j and E are written in the form (4.2.1),
then o must be written as the dyad
o=o
xx
ii +o
xy
ij+o
xz
ik+o
yx
ji+
+o
yy
jj+o
yz
jk+o
zx
ki +o
zy
kj +o
zz
kk
(4.2.7)
If the vectors and E are written in the column matrix form , then must be written as the square matrix
o=
(
o
xx
o
xy
o
xz
o
yx
o
yy
o
yz
o
zx
o
zy
o
zz
)
(4.2.8)
Whatever representation is used, if the components of (4.2.6) are written out explicitly, the same result
obtains:
j
x
=o
xx
E
x
+o
xy
E
y
+o
xz
E
z
j
y
=o
yx
E
x
+o
yy
E
y
+o
yz
E
z
j
z
=o
zx
E
x
+o
zy
E
y
+o
zz
E
z
(4.2.9)
Tensor manipulations are simplified considerably by the use of the following notation. The set of
equations (4.2.9) can be written
j
o
=

=x , y , z
o
o
E

, o=x , y , z
(4.2.10)
The summation sign is now omitted, and the Einstein summation convention introduced: when a Greek
suffix occurs twice in the same term, summation with respect to that suffix is understood. Thus (4.2.10)
is now written
j
o
=o
o
E
(4.2.11)
pag 5 [23]
EXAMPLE 1.1-2. For
y
i
=a
ij
x
j
i,j = 1, 2,3 and
x
i
=b
ij
z
j
; i,j = 1, 2,3 solve for the y variables in
terms of the z variables.
In matrix form thr given equation can be expressed:
(
y
1
y
2
y
3
)
=
(
a
11
a
12
a
13
a
21
a
22
a
23
a
31
a
32
a
33
)(
x
1
x
2
x
3
)
and
(
x
1
x
2
x
3
)
=
(
b
11
b
12
b
13
b
21
b
22
a
23
b
31
b
32
b
33
)(
z
1
z
2
z
3
)
Now solve for the y variables in terms of of the z variables and obtain
66
(
y
1
y
2
y
3
)
=
(
a
11
a
12
a
13
a
21
a
22
a
23
a
31
a
32
a
33
)(
b
11
b
12
b
13
b
21
b
22
a
23
b
31
b
32
b
33
)(
z
1
z
2
z
3
)
y
n
=a
nm
x
m
, n , m=1,2,3
and
x
m
=b
mj
z
j
, m, j =1,2,3
the index notation employs indices that are dummy indices and so we can write
Here we have purposely changed the indices so that when we substitute for x
m
, from one equation into the
other, a summation index does not repeat itself more than twice. Substituting we find the indicial form of the
above matrix equation as
y
n
=a
nm
b
mj
z
j
, m, n , j =1,2,3
where n is the free index and m, j are the dummy summation indices. It is left as an exercise to
expand both the matrix equation and the indicial equation and verify that they are different ways of
representing the same thing(see formula (5.2.2)and (5.2.3)).
So the problem is to represent the polarisability in space-fix system through polarisability of molecule
in molecule-fixed system components.
o(o
xx
, o
yy
, o
zz
)= f (o
(
, o
j
,o

)
or
o(o
xx
, o
yy
, o
zz
)= f (o

, o

)
because e from pag 162 [20]
when the field is at some angle to axis you must to resolve it into perpendicular and parallel
components and multiply each by pertinent polarizability
p=o

+o

pag 36 [21]
suppose that we have two systems molecular frame-work c with axis (, j, and a space fixed
frame-work i with x , y , z axis.
Suppose that principal axis of polarizability of ellipsoid coincide with the axis of molecular frame so
we have a diagonal form for tensor of polarizabilty
(
o
(
0 0
0 o
j
0
0 0 o

)
(5.2.1)
p
c
=

c
p
c
(c j )
(5.2.2)
Expanding we have (see pag 49 [22])
67

p
x
=p
(
(( x)+p
j
(j x)+p

(x)
p
y
=p
(
(( y)+p
j
(j y)+p

( y)
p
z
=p
(
((z)+p
j
(j z)+p

(z )
(5.2.3)
(a)

p
x
=p
(
(( x)+p
j
(j x)+p

(x)
p
y
=p
(
(( y)+p
j
(j y)+p

( y)
p
z
=p
(
((z)+p
j
(j z)+p

(z )

p
x
=p
(
cos(( , x)+p
j
cos(j , x)+p

cos( , x)
p
y
=p
(
cos((, y)+p
j
cos (j , y)+p

cos(, y)
p
z
=p
(
cos(( , z)+p
j
cos (j , z)+p

cos( , z )
these are the directions cosines
we can proof by taking into account that in laboratory system we have
p=p
x
x+p
y
y+p
z
z
(b)
and by the other hand in molecular frame we have
p=p
(

(+p
j
j+p

(c)
taking into account orthogonality relations we have
from (b) px=p
x
(xx)+p
y
(yx)+p
z
(zx)=p
x
from (c) px=p
(
(

(x)+p
j
(jx)+p

x)
so (b) =(c) (a)
(

(x)=

(xcos((, x)=11cos((, x) or simple ((x)

in this way we have defined the directions cosines.
pag 85 [23]
moreover we have the following relations pag 174[18]and pag 353 [17]
that
l =
x
r
, m=
y
r
, n=
z
r
that is a set of angles
since r
2
=x
2
+y
2
+z
2
then l
2
+m
2
+n
2
=1 so we have that
r
1
r
2
= r
1
r
2
cos( r
1
r
2
)=x
1
x
2
+y
1
y
2
+z
1
z
2
r
1
r
2
= r
1
r
2
cos( r
1
r
2
)=x
1
x
2
+y
1
y
2
+z
1
z
2
(5.2.4)
suppose that we have two systems molecular frame-work c with axis (, j, and a space fixed
frame-work i with x , y , z axis.
We express x axis throughout (, j, we have
x=xcos( x , ()

(+xcos( x ,j)j+xcos( x ,)

y=ycos( y ,()

(+ycos( y ,j)j+ycos( y , )

z=zcos( z ,()

(+zcos( z , j)j+zcos( z , )

x=1 and

(=1 j=1

=1
x=cos( x , ()+cos( x ,j)+cos( x ,)
using (5.2.4)
xx=1=cos
2
( x ,()+cos
2
( x ,j)+cos
2
( x , )
yy=1=cos
2
( y , ()+cos
2
( y ,j)+cos
2
( y ,)
zz=1=cos
2
( z , ()+cos
2
( z ,j)+cos
2
( z , ) or
68
( x , ()
2
+( x , j)
2
+( x ,)
2
=1
( y , ()
2
+( y , j)
2
+( y ,)
2
=1
( z ,()
2
+( z ,j)
2
+( z ,)
2
=1
(5.2.5)
the other products due to orthogonality are zero
xy=( x ,()( y , ()+( x , j)( y , j)+( x ,)( y , )=0
xz=( x ,()( z , ()+( x ,j)( z ,j)+( x , )( z ,)=0
zy=( z ,()( y ,()+( z , j)( y , j)+( z , )( y ,)=0
(5.2.6)
(5.2.6) and (5.2.5) ,(5.2.7)are called orthonormality relations and all can be combined in (5.2.21).
Now the same thing for other set
We express c axis throughout x , y , z we have

(=

(cos((, x)x+

(cos(( , y) y+

(cos(( , z) z
j= jcos(j , x) x+ jcos(j , y) y+jcos(j, z)z

cos(, x) x+

cos( , y) y+

cos(, z )z
we obtain
( x , ()
2
+( y ,()
2
+( z , ()
2
=1
( x ,j)
2
+( y , j)
2
+( z , j)
2
=1
( x , )
2
+( y , )
2
+( z , )
2
=1
(5.2.7)
And for the last set the same.
or pag 353 [17]
p
j
=

i
a
ji
E
i
, i , j =x , y , z
(5.2.8)
p
c
=a
c
E
c
=a
c

i
E
i
(ci )
(5.2.9)
First we will expand the following relation
E
c
=

i=x , y , z
E
i
(ci )
we have

E
(
=E
x
(( x)+E
y
(j y)+E
z
(z )
E
j
=E
x
((x)+E
y
(j y)+E
z
( z)
E

=E
x
(( x)+E
y
(j y)+E
z
( z)
(d)
69
so
p
c
=a
c
E
c
=a
(
E
(
+a
j
E
j
+a

by using (d)
we have
p
c
=a
(
| E
x
((x)+E
y
(j y)+E
z
(z)
+a
j
| E
x
(( x)+E
y
(j y)+E
z
(z)
+a

| E
x
(( x)+E
y
(j y)+E
z
(z)
we made the substitution (5.2.9) into (5.2.2)
p
j
=

i

c
a
c
(ci )(c j ) E
i
(5.2.10)
No we compare (5.2.8) with (5.2.10) we obtain:
a
ij
=a
ji
=

c
a
c
(ci )(c j )
(5.2.11)
(5.2.11) Is the law of transformation of a symmetric tensor of rank two. Or taking into account
(5.2.5)and(5.2.6) we have
a
xx
=a
(
(( x)
2
+a
j
(j x)
2
+a

(x)
2
a
yy
=a
(
(( y)
2
+a
j
(j y)
2
+a

( y)
2
a
zz
=a
(
((z)
2
+a
j
(j z)
2
+a

(z)
2
(5.2.12)
The other is zero.
Let us calculate the components of electrical polarization vector

P in space coordinates
P
j

k=1
N
1
p
j
( k)
=

k=1
N
1

i

c
a
sigma
( k)
(ci )(c j ) E
i
index k number the molecules.
As all molecules as the same and are set up randomly i.e. any direction or orientation of system
(, j, with respect to system x, y , z are equals (isotropic system)so:
P
j
=N
1

i

c
a
c
(ci )(c j ) E
i
(5.2.13)
So taking into account (5.2.15) we have
P
j
=N
1
E
j
3

c
a
c
Pag 32[21]
70
c \i x y z
( coscos0cos
sin sin
sincos0cos+
+cossin
sin0cos
j coscos0sin
sin cos
sincos0sin +
+coscos
sin0sin
cossin0 sinsin0 cos0
Table 1.9 Elements of the direction cosine matrix
D
c i
or Euler Angles
this rotation matrix can be obtained by the tree matrices describing three rotations see [24]pag 203
R
z
()=
(
cos sin 0
sin cos 0
0 0 1
)
R
y
(0)=
(
cos 0 0 sin0
0 1 0
sin 0 0 cos 0
)
R
z
()=
(
cos sin 0
sin cos 0
0 0 1
)
these are obtained from successive application of formula (4.2.2)
and
D(, 0, )=R
z
() R
y
(0) R
z
()
28 (5.2.14)
You must finish here see pag 56 [69]and pag [60].
pag 361 [17]:
71
or like in [17] pag 363
see also pag 134 & 138 [21]
c \i x y z
( ((x) (( y) ((z)
j (j x) (j y) (j z)
( x) ( y) (z)
So we have 9 unknown quantity and the people manage so that by rotation to reduce to 3 quantities
further if the system axis coincide with principal axes this tensor is said to be diagonalised.
So in spherical coordinates 0 coincides with polar angle than the isotropic averages of products of
the same direction cosine take the form
f (ci ) ,(t k) , ...=

0
2n

0
2n

0
n
f d d sin 0d 0

0
2n

0
2n

0
n
d d sin0d 0
=
1
8n
2

0
2n

0
2n

0
n
f d d sin 0d 0 (5.2.15)
72
Illustration 4
(ci )
2
=(c z)
2
=cos
2
0=
1
3
(5.2.16)

cos
2
0sin0d 0=

t =cos 0
dt sin0d 0

t
2
dt=
t
3
3

n
0
=
2
3
and
(ci )(c j )=(ci )(t j )=(c i )(ti )=0 (5.2.17)
Or combine (5.2.16) and (5.2.17) in one
(ci )(t j )=
1
3
6
ct
6
ij
(5.2.18)
Now we can prove the famous bond polarizability model pag480 [21] and pag 151,162[25]
If we assign to each bond in molecule a own tensor of polarizability with the values
c
nm
n the
number of bond and m=1,2,3. In according with optical valence scheme one of principal axis of
ellipsoid is directed along of one bond so the other axis are perpendicular to the first. So we can:
a
cj
=

n
a
cj
(n)
(5.2.19)
where
a
cj
( n)
=

m=1
3
o
nm
(nmc)(nmj)
So we have the same model between (5.2.19) and (5.2.11) .
We can go further and simplify the problem by assuming that
o
n1
and
o
n2
=o
n3
as for the case of
axially-symmetric molecules(
C
v
D
h
C
3v
pag 186 [18])
So the (5.2.11) or (5.2.12) take the form
a
cj
( n)
=o
n1
(n1c)(n1j)+o
n2
(n2c)(n2 j)+(n3c)( n3j) (5.2.20)
From the orthogonality relations (5.2.5) ,(5.2.6) and (5.2.7)of (5.2.17) we can write them in one
sentence:

(n1c)(n1j)+(n2c)(n2j)+(n3c)(n3j)=6
c j
(5.2.21)
Is follow that
a
c j
( n)
=o
n1
(n1c)(n1j)+o
n2
(n2c)(n2 j)+(n3c)( n3j)+(n1c)(n1j)(n1c)(n1j)
a
c j
( n)
=(o
n1
o
n2
)(n1c)(n1j)+o
n2
6
cj
(5.2.22)
Or in the notation of pag 151[25]
73
o
o
=(o

)u
o
u

+o

6
o
(5.2.23)
Where u is a unit vector and his components are:
u
o
uo=u
1
u
1
+u
2
u
2
+u
3
u
3
if you have a look to (5.1.1),(A 10.5.8),(A 10.5.12),(A 10.5.14)
You see that every tensor can be decomposed in two parts isotropic part and anisotropic.
The isotropic part have diagonal form see (5.2.1) and can be represented as
1
3
(o

+2o

)
so now our task to put this result in the last term of (5.2.2) we get:
o

6
o
=
1
3
(o

+2o

)6
o

1
3
(o

)6
o
(5.2.24)
Substituting (5.2.24) in (5.2.23) we get
o
o
=
1
3
(o

+2o

)6
o
+(o

)(u
o
u

1
3
6
o
)
(5.2.25)
(5.2.25) Is the formula (7) in [26]
so the (5.2.25) have two parts isotropic the first term and anisotropic the second term.
Chapter 6 Fine structure
6.1 Angular Momentum
J
2
ctrl +b ctrl sift+b J
2
ctrl shift +p

Have to write all points indicated from Carlos
[1] C.J. Foot, Atomic Physics , Oxford 2005
[2] C. Gerry, Introductory Quantum Optics, Cambridge 2005
[3] E. Kartheuser , Elements de MECANIQUE QUANTIQUE , Liege 1998?!
[4] M. Kuno, Quantum mechanics, Notre Dame, USA 2008
[5] M. Kuno, Quantum spectroscopy, Notre Dame,USA 2006
[6] I. Savelyev, Fundamental of theoretical Physics,Moscow 1982
[7] I. Savelyev, Physics: A general course vol. I,III,III, Moscow 1980
[8] .. . [ 5, 1]
[9] K. Riley, M. Hobson, Mathematical Methods for Physics and Engineering: A Comprehensive
Guide, Second Edition, Cambridge 2002
[10] . . , M 1991
[11] S. Blundell, Magnetism in condensed matter,Oxford 2001
[12] P. Atkins, Physical Chemistry
[13] H. Eyring , Quantum Chemistry, New-York, London (1944)
[14] J. Sakurai, Modern quantum mechanics, 1993
[15] A. Matveev , , Moscow 1989
74
[16] . , , 2001
[17] A. Messiah, Quantum mechanics
[18] G. Arfken, H. Weber, Mathematical Methods For Physicists, International Student
Edition(2005)
[19] C. Clark , Angular Momentum, 2006 august (5 pag)
You must to know
Larmor precession
spin
Stern Gerarch experiment
spin orbit coupling
spin spin coupling
optical transitions
slater determinat from [6]
Master equation
pag 84 [7] angular momentum

M
2
and three operators of the projections of angular momentum

M
x

M
y

M
z
It was found that only the square of the angular momentum and one of the projections of the angular
momentum onto the coordinate axes can simultaneously have definite values.
The solution of the equation

M
2
=M
2

(6.1.1)
is very difficult(see the master thesis ). We shall therefore only give the final results: the eigenvalues of the
operator of the square of the angular momentum are
M
2
=l (l +1) (l =0,1,2,3, ...) (6.1.2)
Here l is a quantum number called the azimuthal (or orbital) one. Consequently, the magnitude of the
angular momentum can have only discrete values determined by the formula
M=.l (l +1) (l =0,1,2,3, ...) (6.1.3)
M
z
=m
m=0,!1,!2 ,!3, ... ,!l (6.1.4)
2l +1values from !l2+1
or
75
pag 197 [8]
For reasons which will be revealed on a later page, m is called the magnetic quantum number. We remind
our reader that quantization of the projection of the angular momentum was discovered experimentally by O.
Stern and W. Gerlach (see Sec. 7.6 of Vol. II, p. 170).
pag 135 [36]
pag 120 [16]
pag 170 [34] vII
The charge e + , where e is the charge of an electron and + is its number of revolutions a second see
fig 7.10
I =
Aq
At
=
e
T
=e+
p
m
=IS=e +nr
The product v=2nr + gives the speed of the electron v, therefore we can write that
76
Diagram: On the z axis we see the different m values that is regarded as
the projection of

l onto z axis, with the length of .l (l +1)

1
1
0 0
1
1
2
2
.2
.6
(a) (b)
p
m
=
e v r
2
The moment (7.39) is due to the motion of an electron in orbit and is therefore called the orbital magnetic
moment. The direction of the vector p
m
forms a right-handed system with the direction of the current, and a
left-handed one with that of motion of the electron (see Fig. 7.10).
An electron moving in orbit has the angular momentum
L=mv r
here we have in terms of modulus, where (m is the mass of an electron). The
vector

L is called the orbital angular momentum of an electron. It forms a right-handed

system with the direction of motion of the electron. Hence, the vectors p
m
and

L
are directed oppositely.
The ratio of the magnetic moment of an elementary particle to its angular momentum is
called the gyromagnetic (or magnetomechanical) ratio. For an electron, it is
p
m
L
=
e
2m
(6.1.5)
An electron moving in orbit has the angular momentum an electron has its intrinsic angular momentum

L
s

and magnetic moment p
m ,s
for which the gyromagnetic [,darmgntk] ratio is
p
m,s
L
s
=
e
m
(6.1.6)
Attempts were initially made to explain the existence of the intrinsic magnetic moment and angular momentum
of an electron by considering it as a charged sphere spinning about its axis. Accordingly, the intrinsic angular
momentum of an electron was named its spin. It was discovered quite soon, however, that such a notion results
in a number of contradictions, and it became necessary to reject the hypothesis of a "spinning" electron. It is
assumed at present that the intrinsic angular momentum (spin) and the intrinsic (spin) magnetic moment
associated with it are inherent properties of an electron like its mass and charge.
The magnetic moment of an atom consists of the orbital and intrinsic moments of the electrons in it, and also of
the magnetic moment of the nucleus (which is due to the magnetic moments of the elementary particles -
protons and neutrons_forming the nucleus). The magnetic moment of a nucleus is much smaller than the
moments of the electrons. For this reason, they may be disregarded when considering many questions, and we
may consider the magnetic moment of an atom to equal the vector sum of the magnetic moments of its electrons.
The magnetic moment of a molecule may also be considered equal to the sum of the magnetic moments of all its
electrons.
F=p
m
B
x
x
cos o (6.1.7)
Instead of a continuous extended trace, separate lines were obtained that were arranged symmetrically with
respect to the trace of the beam obtained in the absence of a field.
The Stern-Gerlach experiment showed that the angles at which the magnetic moments of atoms are oriented
77
relative to a magnetic field can have only discrete values, i.e. that the projection of a magnetic moment onto the
direction of a field is quantized.
So in absence of a field we obtain a continuous spectra but in the presence of the field we obtain a discrete
spectra.
We have :
d L=T dt d L=p
m
Bsinodt
d 0=
d L
Lsin o
=
p
m
Bsin odt
Lsin o
o
l
=d
0
dt
=
p
m
L
B
o
l
=
e B
2m
(6.1.8)
Larmor frequency
pag 103 [7] III
investigations of the optical spectra of alkali metal ions showed that the angular momentum of the atomic
residue (i.e. of the nucleus and the remaining electrons except for the most loosely attached valence electron that
leaves the atom in ionization) is zero. Hence, the angular momentum of an alkali metal atom equals that of its
valence electron, and L of the atom coincides with l of this electron.
Pag 169 [7] II
Not only electrons, but also other elementary particles have a spin. The spin of elementary particles is an
integral or half integral multiple of the quantity equal to Planck's constant h divided by 2n
=
h
2n
=1.0510
34
Js=1.0510
27
ergs
In particular, for an electron, L
s
=
1
2
in this connection, the spin of an electron is said to equal
1
2
. Thus,
78
Illustration 6: fig
d

L

L
o'
o
d 0

T
p
m

B
r '
e
Illustration 5:
d

L

L
o'
o
d 0

T
p
m

B
r '
e
Illustration 7
d

L

L
o'
o
d 0

T
p
m

B
r '
e
is a natural unit of the angular momentum like the elementary charge e is a natural unit of charge.
In accordance with , the intrinsic magnetic moment of an electron is
p
m
=
e
m
L
s
=
e
m

2
=
e
2m
the quantity
j
B
=
e
2m
=0.92710
34
J/ T=0.92710
20
erg/Gs
(6.1.9)
is called Bohr magnetron
in Gaus
j
B
=
e
2m
e
c
pag 109 [7] II
The structure of a spectrum reflecting the splitting of the lines into their components is called fine structure.
The complex lines consisting of several components are known as multiplets.
To explain the splitting of these levels, the Dutch physicists Samueli Goudsmit and George Uhlenbeck in 1925
advanced the hypothesis that an electron has an intrinsic angular momentum M
s
not associated with
the motion of the electron in space. This intrinsic angular momentum was called spin.
It was initially assumed that spin is due to rotation of an electron about its axis. According to these notions, an
electron was considered similar to a top or spindle. This explains the origin of the term "spin". Very soon,
however, it became necessary to reject such model ideas, in particular for the following reason. A spinning
charged sphere must have a magnetic moment, and the ratio of the magnetic moment to the mechanical angular
momentum must be
j
B
M
=
e
2m
e
c
Indeed, it was established that an electron in addition to its intrinsic mechanical angular momentum has an
intrinsic magnetic moment j
s
. A number of experimental facts, however, in particular the complicated
Zeeman effect, witness that the ratio between the intrinsic magnetic moment and intrinsic mechanical angular
momentum is double (see (5) and (6) )that between the orbital magnetic moment and orbital mechanical angular
momentum
j
s
M
s
=
e
m
e
c
Thus, the notion of an electron as of a spinning sphere was unfounded. Spin must be considered as an
intrinsic property characterizing an electron in the same way as its charge and mass to.
The magnitude of the Intrinsic angular momentum of an electron is determined according to the general laws of
quantum mechanics by the so-called spin quantum number s equal to 1/2, for a proton and a neutrons also
equals one-half, for a photon, s equals unity.
M
s
=. s( s+1)=
.
1
2

3
2
=
1
2
.3
79
The projection of the spin onto a given direction can take on quantized values differing from one another by

M
s , z
=m
s
, where (m
s
=!s=!
1
2
)
The projection of the intrinsic magnetic moment of an electron onto a given direction can have the following
values:
j
s , z
=
e
m
e
c
M
s , z
=
e
m
e
c
m
s
=
e
m
e
c
(!1/ 2)=!j
B
the minus sign is obtained if m
s
=+1/ 2 and the plus sign if m
s
=1/ 2
Thus the projection of the intrinsic angular momentum of an electron can take the values of +
1
2
and

1
2

and of intrinsic magnetic moment +j
B
and j
B
Pag 111 [7] III
The angular momentum of the electron will consist, on the other hand, of two momenta: the orbital angular
momentum M
l
due to the motion of the electron in the atom and the spin angular momentum M
s
not
associated with the motion of the electron in space. The resultant of these two momenta gives the , total angular
momentum of the valence electron. Summation of the orbital and spin angular momenta to obtain the total
momentum is performed according to the same quantum laws used to summate the orbital angular momenta of
different electrons . The magnitude of the total angular momentum M
j
is determined by the quantum number
j:
M
j
=. j ( j +1)
Here j can have the values
j =l +s ,l s
where l and s are the azimuthal and spin quantum numbers, respectively. When l = 0, the quantum number j has
only one value, namely, j =s=
1
2
. When l differs from zero, two values are possible: j =l +
1
2
and
j =l
1
2
that correspond to two possible mutual orientations of the angular momenta M
l
and M
s

"parallel" and "antiparallel"
We shall now take into consideration that magnetic moments are associated with the mechanical angular
momenta. The magnetic moments interact with each other like two currents or two magnetic pointers do.
The energy of this interaction (called spin-orbit interaction coupling) depends on the mutual orientation
of the orbital and intrins angular momenta. Hence, states with different j's must have different energy.
My explanation(how interact the angular momentum and magnetic angular momentum both tend to rotate the
electron maybe in different directions so both tend to control the electron this is called the interaction)
o is a dimensionless quantity called the fine structure constant. It is determined by the expression
o=
e
c
=
1
137
80
6.2 Atom with Many Electrons
1. The angular momenta M
l
have a stronger interaction with one another than with the M
s
's which,
in turn, are coupled more strongly to one another than to the M
l
's. Consequently, all the M
l
's
add up to form the resultant M
L
and the angular momenta M
s
, add up to form M
S
and only
now do M
L
and M
S
give the total angular momentum of the atom M
J
. Such a kind of
coupling is encountered most frequently and is known as the Russell-Saunders or LS coupling.
2. Each pair of the
M
l
's and
M
s
's displays a stronger interaction between the partners of the pair
than between an individual partner and the other M
l
's and M
s
's. Consequently, resultant M
j
's are formed for each electron separately and they then combine into the M
J
. This kind of atom is
called jj coupling is observed in heaven atoms.
So in Savelyev you have pag 131[7] III
! .
! .
! .
! .
! .

!1/ 2
!1/ 2
!1/ 2
!1/ 2
!1/ 2
so you must take into account maybe that LS coupling occur and the filling of states start
up from parallel and finished with antiparallel !? Or by the rule of triangle of a vector summation we put tail to
tip tail to tip
Pag 582 [3]

n
i
(r
i
)=R
n,l
(r
i
)Y
l , ml
(0
i
,
i
)
(6.2.1)
where n
i
represents the set of quantum numbers

n
i
=

n=1,2,. ..
l =0,1,2,. .. n1
m
l
=l , ...+l

n
i
=

n=1,2,. ..
l =0,1,2,. .. n1
m
l
=l ,...+l
(6.2.2)

x=a+b
y=c+d
pag 116 ,III [7]
81
The term of an atom is conventionally written as follows
L
J
2S+1
(6.2.3)
Where L stands for one of the letters S, P, D, F, etc.
pag 585 [3]
the term in the Russell-Saunders representations where 2 S+1 is the multiplicity of level and J
is the total angular moment

J =

L+

S (6.2.4)
i.e. for iron atom who corresponds to L=2 and S=2 J =2+2=4 is indicated by
D
4
5
pag 130 [7] III

The rules:
shells 2 n see below
sub-shells 2(2l +1) see above
pag 135+144 [10] and 584 [3]
why 2n because from Pauli principle we have two different states have n for m
s
=+1/ 2 and n for
m
s
=1/ 2
A completely filled sub-shell is characterized by the equality to zero of the total orbital and total spin angular
momenta ( L=0, S=0 ). Hence, the angular momentum of such a subshell equals zero ( J =0 ). Let us
convince ourselves that this is true taking the 3d-subshell as an example. The spins of all ten electrons in this
subshell compensate one another in pairs, and as a result S=0 . The quantum number of the projection of the
resultant orbital angular momentum M
L
of this subshell onto the z-axis has the single value
m
L
=

m
l
=0 . Consequently, L also equals zero. Thus, when determining L and S of an atom,
no attention may be given to filled subshells.
1. From Hund's first rule S
max
2. like in table 5.2 pag 130 [7] III, sketch the spins so that
S
max
m
S
=

m
s
3. m
L
=

m
l
4. from Hund's second we chose the
J
max

by two empirical Hund's rules:
1. Of the terms belonging to a given electron configuration, the term with the greatest possible value of S
and with the greatest possible value of L at this S will have the lowest energy.
2. The multiplets formed by equivalent electrons are normal (this signifies that the energy of the state
grows with an increase in J) if not more than half of the subshell is filled, and are inverted (the energy
diminishes with an increase in J) if more than half of the subshell is filled. It follows from Hund's
second rule that when not more than half of a subshell is filled, the component of the multiplet with
J =LS has the lowest energy, otherwise the component with J =L+S has such an energy.
82
See pag 32 [37]
(1) Arrange the electronic wave function so as to maximize S. In this way the Coulomb energy is minimized
because of the Pauli exclusion principle, which prevents electrons with parallel spins being in the same place,
and this reduces Coulomb repulsion between electrons.
(2) The next step is, given the wave function determined by the first rule, to maximize L. This also minimizes the
energy and can be understood by imagining that electrons in orbits rotating in the same direction can avoid each
other more effectively and therefore reduce Coulomb repulsion.
(3) Finally the value of J is found using J =LS if the shell is less than half full and J =L+S if it
is more than half full. This third rule arises from an attempt to minimize the spin-orbit energy.
Pag 583 [3]

L=

i=1
N

L
i
or

M=

i =1
N

M
i
(6.2.5)
The same for spin

S=

i =1
N

S
i
(6.2.6)
Pag 113 Condon [53]
without j
pag 33 [11]
S P D F G H I
L = 0 1 2 3 4 5 6
My examples
ex1:
23V
3d
3

x
x
!
!
!

S=
1
2
+
1
2
+
1
2
=
3
2

x
x
0
+1
+2

L=2+1 this mean that we have a symbol F see pag 158 [36]
83
3
3
2
=
3
2
F
3/ 2
4
ex2:
25Mn
3d
5

!
!
!
!
!

S=
1
2
+
1
2
+
1
2
+
1
2
+
1
2
=
5
2

2
1
0
+1
+2

L=2+112=0S
S
5/ 2
6
ex3:
27Co
3d
7

!
!
!
!
!

x
x
x
.
.

S=
1
2
+
1
2
+
1
2
+
1
2
+
1
2

1
2

1
2
=
3
2

2
1
0
+1
+2

x
x
x
+1
+2

L=2+112+1+2=3F
J =3+
3
2
=
9
2
F
9/ 2
4
for more details or another confirmations see
Example from pag 33 [11] or see pag 57[10]
84
Illustratio
n 8
As an example, consider the rare earth ion
Dy
3+
, which has outer shell
4 f
9
: f electrons have l =3 ,
so to satisfy Hund's first rule, 2l +1=7 of them are spin-up, and we then have 2 left for spin-down (see
Illustration 8). This gives the value of S as S=7
1
2
2
1
2
=
5
2
(which implies that the spin degeneracy
is 2 S+1=6 ). The spin-up electrons give no net orbital angular momentum, so we only get an orbital
contribution from the 2 spin-down electrons and it is this which we have to maximize. This then implies that
L=3+2=5 and hence we must use the symbol H. The .shell is more than hall full, so J =5+
5
2
=
15
2
.
Hence the term symbol is H
15/ 2
6
.
Energy levels:
left is fine
structure of
sodium and
right is the
lines of the
series of a
sodium (Na)
atom that can
be represented
as transitions
between the
energy levels
see pag 212 [52]
As a first example, consider a hypothetical excited electronic state of lithium.
85

3
2
1
0
1
2
3

!
!
!
!
!
!
!

!
!

1s
1
2 p
1
3 p
1
All three electrons are in different shells and, hence, non equivalent. The orbital angular momentum of
each electron is defined as

l
1
,

l
2
,

l
3
. The first step is to determine the resultant orbital angular
momentum of the first two electrons,

L
12
. This is determined first because the quantum number for
the magnitude of a resultant angular momentum vector may take on the values from the sum of the two
sources down to the absolute value of their differences. In this example,
l
1
=0
for electron 1 and
l
2
=1
for electron 2. The magnitude of the vector sum

L
12
is equal to only 1.

L
12
=

l
1
+

l
2
L
12
=1
The orbital angular momentum vector

l
3
of the third electron, is now added to

L
12

L
12
+

l
3
=

L
total
L
total
=1+1,. .. ,11=2,1,0
This result means that there are three possibilities in the coupling of orbital angular momentum with
intrinsic spin angular momentum.
The total intrinsic spin angular momentum is determined in the same fashion.
See the pag 569 [48]
L>S we have the numbers of terms (2 S+1)

J =LS
L+S
(2 J +1)=

J =LS
L+S
(2 J +1)=
1
2
(2 S+1)| 2( L+S)+1+2( LS)+1=(2 S+1)(2 L+1) (6.2.7)
LS we have the numbers of terms (2 L+1)

J =LS
L+S
(2 J+1)=

J =LS
L+S
(2 J+1)=
1
2
(2 L+1)| 2(S+L)+1+2(SL)+1=( 2S+1)( 2 L+1)
e.g. we have the series :
1 2 3 ... l
l l 1 l 2 ...1
the sum of this series is a arithmetical progression sum up
we get that each term is l +1=2+l 1=... , we have l terms the sum will be (l +1)
l
2
for many electrons atoms see pag 149 [36] we have
L=(l
1
+l
2
) , ( l
1
+l
2
1) , ... ,l
1
l
2

(6.2.8)
so can be equal to
2l
1
+1 2l
2
+1
different values we will pick up the little value from two l .
e.g.
l
1
=2
and
l
2
=3
we obtain 22+1=5 different values L: 5, 4, 3, 2, 1 without 0! because
we will extract from
l
1
the
l
2
only
l
2
times
l
1
>l
2
.
86
see [49] and [50]
6.104. How many and which values, of the quantum number d can an atom possess in the state with
quantum numbers S and L equal respectively to (a) 2 and 3; (b) 3 and 3; (c) 5/2 and 2?
6.104 The rule is that if

J =

L+

S then / takes the values LS to L+S in step of 1. Thus :

(a) The values are 1, 2, 3, 4, 5
(b) The values are 0, 1, 2, 3, 4, 5, 6
(c) The values are
1
2
,
3
2
,
5
2
,
7
2
,
9
2
In order to understand pag 134 [34] see pag 151 [36]
In establishing the kind of terms possible with a given electron configuration, we must bear in mind
that the Pauli principle does not allow all the combinations of the values of L and S that follow from
the configuration. For example, with the configuration np
2
(two electrons with the principal quantum
number n and l = 1), the possible values of L are 0, 1, 2(
l
1
=1
and
l
2
=1
), while S can have
the values 0 and 1(
s
1
=
1
2
and
s
2
=
1
2
). Accordingly, the following terms would seem to be
possible:
L=0S
L=1P
L=2D
and
2 S+1=20+1=1singlets
2S+1=21+1=3triplets
so we have S
1
P
1
D
1
S
3
P
3
D
3
According to the Pauli principle, however, only such terms are possible for which the values of at least
one of the quantum numbers
m
l
, and
m
s
for equivalent electrons (i.e. electrons with the same n
and l ) do not coincide (This requirement vanishes for non-equivalent electrons, i.e. electrons
differing either in n or in l , or in both of them). The term
3
D, for instance, does not comply with
this requirement. Indeed, L = 2 signifies that the orbital angular momenta of the electrons are
"parallel", consequently, the values of
m
l
for these electrons will coincide. Similarly, S = 1
signifies that the spins of the electrons are also "parallel", therefore, the values of
m
s
also coincide.
As a result, all four quantum numbers (n, l ,
m
l
and
m
s
) are the same for both electrons,
which contradicts the Pauli principle. Thus, the term
3
D in the system of two equivalent electrons
cannot be realized. For more details you can see in [51] because Savelyev have taken from [51] and
maybe is very obsolete.
87
so he pick up the following values
S
0
1
, P
2
3
, P
1
3
, P
0
3
, D
2
1
(6.2.9)
we can understand that if we neglect the negative values from Illustration 9, because on pag 151 [36]
we have only
According to Hund's first rule, one of the P-terms of those given in (6.2.9) must have the least energy
(S is the greatest for these terms). With the configuration np
2
, the subshell p is filled only by one-
third, i.e. less than half. Consequently, according to Hund's second rule, the term with the smallest
value of J, i.e. the term P
0
3
, has the lowest energy.
6.3 The band structure of blue and yellow diamonds
http://www.webexhibits.org/causesofcolor/11A0.html
A pure diamond crystal is translucent, as it is composed only of carbon atoms, each of which has four
valence electrons.
In a yellow diamond, a few carbon atoms per million have been replaced by nitrogen atoms, each
88
Illustration 9
Illustration 10 Illustration 11
containing five valence electrons. The structure of the diamond crystal does not change significantly,
but the extra electrons occupy a donor level.
Synthetic diamond crystals
(3 mm across) grown at
General Electric. The clear
diamond is pure, the blue
contains a boron acceptor,
and the yellow contains a
nitrogen donor.
Electrons can be donated to the empty conduction band. The valence
band is completely filled. At minute concentrations of nitrogen, the
energy required to excite an electron from the donor level to the
conduction band is 4 eV, an energy that is greater than the visible light
range (left). The diamond will be colorless. At a few nitrogen atoms per
million carbon atoms, the donor level is broadened as at the right of this
figure, and energies greater than 2.2 eV can excite an electron from the
donor level to the conduction band. The absorption of these higher
energies (blue and violet light) results in the yellow color of the
diamond.
The nitrogen donor level energy in a diamond is large, peaking at about 4 eV. With a concentration of a
few nitrogen atoms per million, instead of a clean "spike" donor level energy, the nitrogen donor level
energy broadens into a band because of a number of complex factors, including thermal vibrations.
This broadened donor energy band results in the difference between donor and conduction bands being
as low as 2.2 eV. The most likely transition allows incident light with energy of 4 eV per photon to
excite electrons from the donor level to the conduction band. However, it is possible for electrons to be
excited to the conduction band with energy of 2.2 eV and upwards. This means that blue and violet
light are absorbed from the full spectrum of light normally transmitted, and the resulting color is
yellow.
Unlike blue boron-doped diamonds, which conduct electricity, nitrogen-doped diamonds remain
insulators. This is because nitrogen is a deep impurity: a relatively high energy (2.2 eV, as compared
89
Illustration 12
Illustration 13
with 0.4 eV for boron) is required to excite electrons from the donor energy level to the conduction
band, and only a fraction of the available electrons are freed to carry a charge.
An extremely rare green color can result from a higher nitrogen content of about 1 atom per 1000
atoms of carbon. At even higher nitrogen concentrations, the donor level broadens so that all visible
light can be absorbed, resulting in a black color.
Synthetic blue diamonds are created by adding boron as an impurity. Boron is trivalent, having three
valence electrons; where a boron atom replaces a carbon atom in the diamond structure there is one
fewer electron than usual. This missing electron, or hole, creates an acceptor energy level above the
valence band. The boron acceptor energy is only 0.4 eV, so light of any energy can be absorbed during
excitation. The boron acceptor band is broadened, and the absorption tapers off throughout the visible
light energies, resulting in stronger absorption at the red end of the spectrum. At a level of one or a few
boron atoms for every million carbon atoms, an attractive blue color results. Natural diamonds of this
color, such as the Hope Diamond, are rare and highly priced.
Boron has one less electron than carbon, and the presence of a few boron atoms per million carbon
atoms in diamond leads to a hole with an energy level within the band gap. This is called an "acceptor"
level since it can accept an electron from the full valence band.
http://encyclopedia2.thefreedictionary.com/optical+transitio
6.4 optical transition
[ptkl tranzishn]
(physics)
A process in which an atom or molecule changes from one energy state to another and emits or
90
Illustration 14
absorbs electromagnetic radiation in the visible, infrared, or ultraviolet region.
Pag 395 [12]
spectroscopic transitions
6.5 angular momentum deduction
angular momentum deduction all pag 40 [13]= pag 355[3] or see [6] vol II
properties of commutators pag 51 [14]:
| A, A=0 (6.5.1)
| A, B=| B , A (6.5.2)
| A+B , C=| A, C+| B ,C (6.5.3)
| A, BC=| A, BC+B| A,C (6.5.4)
Wikipedia
Lie-algebra relations:
[A,A] = 0
[A,B] = [B,A]
[A,[B,C]] + [B,[C,A]] + [C,[A,B]] = 0
Additional relations: wikipedia
[A,BC] = [A,B]C + B[A,C]
[AB,C] = A[B,C] + [A,C]B
[ABC,D] = AB[C,D] + A[B,D]C + [A,D]BC
[AB,CD] = A[B,CD] + [A,CD]B = A[B,C]D + AC[B,D] + [A,C]DB + C[A,D]B
[[[A,B],C],D] + [[[B,C],D],A] + [[[C,D],A],B] + [[[D,A],B],C] = [[A,C],[B,D]]
[AB,C] = A{B,C} {A,C}B, where {A,B}=AB+BA is the anticommutator
Pag 196 [14] and pag 353 [3]
|

L
x
,

L
y
=|( y p
z
z p
y
) ,( z p
x
x p
z
)
by applying
91
| A+B , C=| A, C+| B ,C we have
|

L
x
,

L
y
=| y p
z
, z p
x
| y p
z
, x p
z
| z p
y
, z p
x
+| z p
y
, x p
z

taking into account that | A, A=0 and | A, BC=| A, BC+B| A,C we get
|

L
x
,

L
y
=| y p
z
, z p
x
+| z p
y
, x p
z
=y p
x
| p
z
, z+ p
y
x| z , p
z
=i | x p
y
y p
x
=i

L
z
| y p
z
, z p
x
=| y p
z
, z p
x
+| y p
z
, p
x
z
| y p
z
, z p
x
=| z , y p
z
p
x
=| z , y p
z
p
x
| z , p
z
y p
x
balasov pag 20
pag 206 [17]

| z , y=zyyz=0
or other proof see pag 175 [15]
|

L
x
,

L
y
=

L
x

L
y

L
y

L
x
=
(

i
)
2
(
y

z
z

y
)(
z

x
x

z
)
(6.5.5)

i
)
2
(
z

x
x

z
) (
y

z
z

y
)
and take care that
y

z
(
z

x
)
=y
(

z
)

x
+y z

z

x
92
so we obtain:
(

i
)
2
(
y

x
+yz

2
z x
yx

2
z
z

2
y x
+zx

2
y z
zy

2
x z
)
+
+
(

i
)
2
(
z

2
x y
+xy

2
z
x

y
xz

2
z y
)
=
(

i
)
2
(
y

x
x

y
)
= i

L
z
1.1 Infinitesimal generators of SU(2) CS (from my master thesis)
The most important commutators relations:
def1:

J
2
=

J
x
2
+

J
y
2
+

J
z
2
(6.5.6)
def2:

=

J
x
!i

J
y
(6.5.7)

J
2
=
1
2
(

J
+

J

+

J

J
+
)+

J
z
2
(6.5.8)
Lemma 1
| J
2
, J
i
=0 (6.5.9)
proof:
will use [A,BC] = [A,B]C + B[A,C] and
|

J
i
,

J
k

=i

l =1
3
e
ikl

J
l
| J
2
, J
z
=| J
x
2
+J
y
2
+J
z
2
, J
z
=| J
x
2
, J
z
+| J
y
2
, J
z
+0=
=| J
z
, J
x
2
| J
z
, J
y
2
=| J
z
, J
x
J
x
J
x
| J
z
, J
x
| J
z
, J
y
J
y
J
y
| J
z
, J
y
=
=i J
y
J
x
i J
x
J
y
+i J
x
J
y
+i J
y
J
x
=0
Lemma 2
| J
2
, J
!
=0
proof:
| J
2
, J
!
=| J
2
, J
x
!i J
y
=| J
2
, J
x
!i | J
2
, J
y
=0
Lemma 3
| J
z
, J
!
=!J
!
proof:
| J
z
, J
x
!i J
y
=| J
z
, J
x
!i | J
z
, J
y
=i J
y
!i (i J
x
)=(!J
x
+i J
y
)=!( J
x
!J
y
)=!J
!
Lemma 4
| J
+
, J

=2 J
z
proof:
93
| J
+
, J

=| J
x
+i J
y
, J
x
i J
y
=i | J
y
, J
x
i | J
x
, J
y
=J
z
+J
z
=2 J
z
belowFirst we must define the problem that is:
taking into account that

J and

J
z
commute they have the same set of eigenfunctions so we must
find out this set that in different books can be represented in different way like:
J
2
a , b=aa , b and
J
z
a , b=ba, b
or
J
2
\, M =\\ , M and
J
z
\ , M=M\, M
and \, M\, M=1
or in Balashov notation

J
2
J
2
, m=J
2
J
2
, m
and

J
z
J
2
, m=mJ
2
, m and J
2
, m

J
2
, m=1

According to ref. [16] (the definition of angular momentum), we introduce the dimensionless
operator which describes the angular momentum L:

J
i
=
1

L
i
i=1,2,3
(1.1)

J
2
=

i =1
3

J
i
2
=

J
1
2
+

J
2
2
+

J
3
2
=

J
x
2
+

J
y
2
+

J
z
2
(1.2)
Those infinitesimal operators obey the following commutation rules:
pag 145 [18]
Levi-Civita Symbol
For future use it is convenient to introduce the three-dimensional Levi-Civita symbol ij k , defined by
123 = 231 = 312 = 1,
321 = 132 = 213 = 1 (in order to memories the inverse of 123 is 321 and make the cycles)
all other ijk = 0.

|

J
i
,

J
k

=i

l =1
3
e
ikl

J
l
(6.5.10)

|

J
i
,

J
k

=i

l =1
3
e
ikl

J
l
(1.3)
|

J
i
2
,

J
k
=0 (1.4)
We introduce the infinitesimal operators which generate the SU(2) CS:

J
+

J
x
+i

J
y
)
(1.5)

J
x
i

J
y
)
(1.6)
Also their self-adjoin proprieties:
(

J
!
)
+
=

(1.7)

J
+

J

=
(

J
x
+i

J
y
) (

J
x
i

J
y
)
=

J
x

J
x
i

J
x

J
y
+i

J
y

J
x
+

J
y

J
y

J
2

J
z
2
i
|

J
x
,

J
y

=

J
2

J
z
2
+

J
z

(1.8)

J
+
=

J
2

J
z
2

J
z
(1.9)
|

J
z
,

J
!

=!

J
!
(1.10)
94
|

J
+
,

J

=2

J
z
(1.11)
Let us consider that we find the complete function set J
2
, m for the commutators:
J
2
, m

J
2

J
z
2
J
2
, m=J
2
m
2
(1.12)
On the other hand:
J
2
, m

J
2

J
z
2
J
2
, m= J
2
, m

J
x
2
+

J
y
2
J
2
, m0 (1.13)
you can imagine the sphere in 1D
J
2
m
2
0 sau m
2
J
2
(1.14)
m
min
mm
max
(1.15)
Let us demonstrate the relation:

J
!
J
2
, m=AJ
2
, m!1 (1.16)
For that we acting by
|

J
z
,

J
!

on function

J
2
, m , and taking into account (1.12) we get:
(

J
z

J
!

J
!

J
z
)
J
2
, m=!

J
!
J
2
, m (1.17)

J
z
(

J
!
J
2
, m
)
=( m!1)
(

J
!
J
2
, m
) (1.18)
Where

J
!
J
2
, m is the eigenfunction of
J
z
operator, with m!1 eigenstates, hence result that
J
2
, m satisfy the (1.16) relation, and acting by

J
+
operator on J
2
, m vector lead to growth of
angular momentum m with a unit, in this reason the

J
+
operator is called creator operator for SU(2)
CS.
For understanding I follow the principle of [18] pag 262
this is for J
2
, m

J
2
J
2
, m=J
2
J
2
, m

J
z
J
2
, m=mJ
2
, m
and this is for (

J
+
J
2
, m) states:

J
2
(

J
+
J
2
, m)=J
2
(

J
+
J
2
, m)

J
z
(

J
+
J
2
, m)=m+1(

J
+
J
2
, m )
where we have taking into account that this
|

J
2
,

J
+
=0
commute but |

J
z
,

J
+
=+

J
+
do not
commute. So we can say that m+1J
2
, m=mJ
2
, m+1 .
The states with
m>m
max
and
mm
min
dont exist:

J
+
J
2
, m
max
0

J
2
, m
min
0

J
+
J
2
, m
max
0
(1.19)
(

J
2

J
z
2

J
z
)
J
2
, m
max
=0
(

J
2

J
z
2
+

J
z
)
J
2
, m
min
=0

J
2
m
max
2
m
max
=0
J
2
m
min
2
+m
min
=0


(1.20)
m
max
2
+m
max
=m
min
2
m
min
m
max
2
m
min
2
=m
max
m
min
or m
min
2
m
max
2
=m
min
+m
max
(m
min
m
max
)(m
min
+m
max
)=m
min
+m
max
95

m
min
m
max
=1
m
min
+m
max
=0
Since the first is impossible the second must be true so:
m
max
=m
min
(1.21)
Doing the following notations:
m
max
=j m
min
=j
,where j 0 (1.22)
because the maximum projection of m onto Y and Y is j (imagine the sphere)
And from (1.20) result that J
2
= j ( j +1) , j mj (1.23)
Thus for the angular momentum operators and their projection on z-axis we have the following
eigenstates and eigenvectors:

J
2
jm=j ( j+1) jm (1.24)

J
z
jm=m jm (1.25)
where m take any semi-integer value from j to j. The jm vectors are the eigenvectors of squared
angular momentum, respective the projection of this operator on z-axis. In what follows let us calculate
the average for the

J
+

J

operators in jm state, so from (8) and (24) we have:

jm

J
+

J

jm= j ( j +1)m
2
m ? (1.26) Balashov here have a mistake must be see also pag
263 [18]
jm

J
+
jm= j ( j +1)m
2
m
jm

J
+

J

jm=

j ' m'
jm

J
+
j ' m' j ' m'

jm
(1.27) see (6.5.14) and (6.5.15) so we
acting on right or on left .
From pag 171 [41] the matrix elements are diagonal over j therefore j
'
take the value j=j' but the number
m
'
=m-1 disappears in final because the other elements are zero:
jm

J
+

J

jm= jm

J
+
jm1 jm1

jm= jm

J
+
jm1
2
(1.28) see (6.5.14) and
(6.5.15)
From (28) and (30) result:
j ( j +1)m
2
m=j
2
+j m
2
m= j
2
m
2
+( j m)=
( j m) ( j +m)+( j m)=( jm) ( j+m+1)
so:
jm

J
+
j , m1=e
i
.
( j m) ( j +m+1)
(1.29)
where =0 is the factor phase. Thus the action of

J
!
operator over standard base is expressed by
equations:

J
+
jm=.
( j m) ( j +m+1) j , m+1

jm=.( j +m) ( j m+1) j , m1

121 (6.5.11)
(1.30)
Which show that

J
+
play the role of any growth operator and

of any diminution
operator for the eigenstates

J
z
.
other proof see [19]:
j , mJ
!
+
J
!
j , m= j , mJ

J
!
j , m
= j , mJ
2
J
z
2
J
z
j , m=
2
| j ( j+1)m
2
m=
2
| j ( j+1)m(m1)
but we also have:
96
j , mJ
!
+
J
!
j , m= j , m!1c
!

c
!
j , m!1=c!
2
c!= . j ( j+1)m(m!1)
J
!
=. j ( j +1)m( m!1) j , m!1
the other best and beautiful demonstration see pag 45 Eyring [13]
So I derived that one but the truth is that I not understand nothing because there are the books
and are the books better and better than other.
See pag 375, 376 [30]
see pag 109 [41]
see pag 198 [46] for harmonic oscillator that is the same
So the problem is that we mast to choose to pick up one representations for which the operators

J
2
and

J
z
are diagonal i.e. the states
j , m
j

or the spherical functions

Y
l , m
(0, )
. So we have
j , m
j

J
z
j
'
, m
j
'
=m
j
6
j ' , j+1
6
m'
j
,m
j

j , m
j

J
2
j
'
, m
j
'
=
2
j ( j+1)6
j ' , j+1
6
m'
j
,m
j
(6.5.12)
97
Illustration 15
Illustration 16

J
+
j , m
j
=C
+
j , m
j
+1 (6.5.13)
From [47] we have that
J
+
and
J

are a Hermitian conjugate pair J

!
=J

j , m
j

J
+

J
+
j , m
j
= j , m
j

J
+
j , m
j
= j , m
j
o

o j , m
j
=o
2

j , m
j

j , m
j
= j , m
j

J
+

J

j , m
j
= j , m
j

j , m
j
=
2
(6.5.14)
Also see pag 330, 331 [30]

is hermitian conjugate of

J
+
so we have we have from (6.5.13):
j , m
j

= j , m
j
+1C
+
(6.5.15)
j , m
j

J
+
j , m
j
=C
+

2
C
+

2
= j , m
j

J
2

J
z
2

J
z
j , m
j

=
2
| j ( j +1)m
j
2
m j , m
j
j , m
j

=
2
|( j m
j
)( j+m
j
+1)
C
+
=| ( j m
j
)( j +m
j
+1)
1
2
the same for

j , m
j
=C

j , m
j
1 (6.5.16)
we obtain

C

=| ( j +m
j
)( j m
j
+1)
1
2
so we have the following matrix elements:
j , m
j
'

J
+
j , m
j
=| ( j +m
j
)( j m
j
+1)
1
2
6
m'
j
, m
j
+1
j , m
j
'

j , m
j
=| ( j +m
j
)( j m
j
+1)
1
2
6
m'
j
, m
j
1
98
Chapter 7 Quantum mechanics and postulates
7.1 The most important thing in Quantum Mechanics
The most important thing in Quantum Mechanics see [45]
Hermitian matrix
A Hermitian matrix is self adjoint: A=A

A
ij
=A
ji

. Hermitian matrices are very important in

quantum mechanics as their eigenvalues are real and their eigenkets are orthogonal, therefore, they are
matrix representations of quantum mechanical operators. Furthermore, Hermitian matrices always
allow diagonalization via a unitary transformation of the sort U

H U , where H is hermitian and

U is unitary. Once diagonalized, Hermitian matrices show the eigenvalues on the diagonal, so in
essence, the quantum mechanical problem of solving Schrdingers equation is replaced by the
problem of diagonalizing the matrix representation of the Hamiltonian in the given basis. When solving
a problem by diagonalizing the matrix representation of the Hamiltonian, one uses the Heisenberg
representation of quantum mechanics; if Schrdingers equation is solved, it is said that the
Schrdinger representation is used. Whatever the representation, the results are equivalent, however in
Heisenbergs representation one does not have to solve the associated second order differential equation
in Schrdingers representation, which can only be solved for the cases when the variables can be
separated.
7.2 Matrix representation of operators:
See pag 94 [31]
The operator call it A can be represented by a matrix A with elements
A
nm
=
n

A
m

which you get by sandwiching the operators between the basis vectors:
A=
(
A
11
A
12
A
13
...
A
21
A
22
A
23
...
A
31
A
32
A
33
...
. . . ...
. . . ...
)
(7.2.1)
7.3 Hermitian Operators
Hermitian Operators
An operator is said to be hermitian if
A
mn

=A
nm
or
A

=A
this dagger symbolises the adjoint of A where A

=( A
T
)

(i.e. take the transpose then take the

complex conjugate).
99
Pag 49 [31]
the complex conjugate of (7.2.1) is
A

=
(
A
11

A
12

A
13

...
A
21

A
22

A
23

...
A
31

A
32

A
33

...
. . . ...
. . . ...
)
Chapter 8 Clebsch-Gordan
8.1 Addition of angular Momenta: Clebsch-Gordan coefficients I
Addition of angular Momenta: Clebsch-Gordan coefficients
see pag 267 [24]
J=J
1
+J
2
(8.1.1)
The equivalent of (6.1.9) is
| J
j
, J
k
=| J
1j
+J
2j
, J
1k
+J
2k
=| J
1j
, J
1k
+| J
2j
, J
2k
=i c
jkl
( J
1l
+J
2l
)=i c
jkl
J
l
also we must take into account that
| J
1i
, J
2i
=0
(8.1.2)
100
J
2
=J
1
+J
2
+J
1+
J
2
+J
1
J
2+
+2J
1z
J
2z
(8.1.3)
proof see pag. 137 [15]
so
J
2
=( J
1x
+J
2x
)
2
+( J
1y
+J
2y
)
2
+( J
1z
+J
2z
)
2
=J
1x
2
+J
2x
2
+J
1x
J
2x
+J
2x
J
1x
+J
1y
2
+J
2y
2
+2 J
1y
J
2y
+J
1z
2
+J
2z
2
+2 J
1z
J
2z
(8.1.4)
J
1x
J
2x
+J
2x
J
1x
=2 J
1x
J
2x
because they commute see (8.1.2)
J
1
=( J
1x
2
+J
1y
2
+J
1z
2
)
2
J
2
=( J
2x
2
+J
2y
2
+J
2z
2
)
2
taking into account (6.5.7)
J
1+
J
2
=( J
1x
+i J
1y
)( J
2x
i J
2y
)=J
1x
J
2x
J
1x
J
2y
+i J
1y
J
2x
i
2
J
1y
J
2y
J
1
J
2+
=( J
1x
i J
1y
)( J
2x
+i J
2y
)=J
1x
J
2x
+J
1x
J
2y
i J
1y
J
2x
i
2
J
1y
J
2y
where the middle terms after the summation vanishes and we obtain (8.1.4)
see the (6.5.9) so in (8.1.3) the first , second and the last terms commute and is zero only:
| J
2
, J
z
=| J
1
J
2+
+J
1+
J
2
, J
1z
+J
2z

=| J
1
, J
2z
J
2+
+J
1
| J
2+
, J
2z
+| J
1+
, J
1z
J
2
+J
1+
| J
2
, J
2z

=J
1
J
2+
J
1
J
2+
J
1+
J
2
+J
1+
J
2
=0
we have the commutators:
| J
2
, J
z
=0 and | J
2
, J
i
2
=0 hence the eigenvalues of J
i
2
, J
2
, J
z
can be used to label the total
angular momentum
J
1
J
2
J M
.
So as the same principle when you have deduced in fact the Clebsch-Gordan coefficients in terms of
raising and lowering operators see above.
So in the same way we have the
J
1
m
1
J
2
m
2

which is the product states that satisfy the

eigenvalue equations:
J
z
J
1
m
1
J
2
m
2
=( J
1z
+J
2z
)J
1
m
1
J
2
m
2
=( m
1
+m
2
)J
1
m
1
J
2
m
2

=MJ
1
m
1
J
2
m
2

J
i
2
J
1
m
1
J
2
m
2
=J
i
( J
i
+1)J
1
m
1
J
2
m
2

but will not have diagonal

J
2
see (6.5.12) except for
maximally stretched states with
M=!( J
1
+J
2
)
see
figure:
101
Fig 17 Coupling of two angular momenta
(a) parallel (b) anti parallel (c) general
case
J
J
2
J
1
J
2
J
2
J
1
J
1
J
J

J
2
J
1
m
1
J
2
m
2
=( J
1
( J
1
+1)+J
2
( J
2
+1)2 m
1
m
2
)J
1
m
1
J
2
m
2

+J
1
( J
1
+1)m
1
(m
1
+1)
1
2
J
2
( J
2
+1)m
2
( m
2
1)
1
2
J
1
m
1
+1J
2
m
2
1
+J
1
( J
1
+1)m
1
(m
1
1)
1
2
J
2
( J
2
+1)m
2
( m
2
+1)
1
2
J
1
m
1
1J
2
m
2
+1
(8.1.5)
the last two terms in (8.1.5) vanish only when
m
1
=J
1
and
m
2
=J
2
or
m
1
=J
1
and
m
2
=J
2
in both case
J =J
1
+J
2
.
In general we have to form appropriate linear combinations of product states:
J
1
J
2
J M=

m
1
,m
2
C( J
1
J
2
Jm
1
m
2
M)J
1
m
1
J
2
m
2

(8.1.6)
The quantities
C( J
1
J
2
J m
1
m
2
M)
in (8.1.6) are called Clebsch-Gordan coefficients.
Exemple see fig 17 (a) :
J
1
J
2
J =J
1
+J
2
M=J
1
+J
2
=J
1
J
1
J
2
J
2

so the Clebsch-Gordan coefficient
( J
1
J
2
J =J
1
+J
2
J
1
J
2
J =J
1
+J
2
)=1
because the eigenvectors are the same e.g. xx=1
8.2 Clebsch-Gordan coefficients (other source)II
Consider a system composed of two parts (1 & 2) with commuting angular momentum operators

J
1
and

J
2
.We can describe the angular momentum states in terms of two sets of commuting operators:
A)

J
1
2
,

J
2
2
,

J
1z
,

J
2z
with eigenvectors
j
1
j
2
m
1
m
2
= j
1
m
1
j
2
m
2

this is uncoupled basis

(2j
1
+1)( 2j
2
+1)
vectors for each
j
1
j
2
B)

J
1
2
,

J
2
2
,

J
2
,

J
z
where

J =

J
1
+

J
2
with the eigenvectors
j
1
j
2
J M
coupled basis
Here the number of eigenvectors for each j
1
, j
2
is given by :
the orbital momentum can have 2 J +1 values this come from J =0,!1,!2,!3, ...

j= j
1
j
2

j
1
+j
2

( 2 J +1) if
j
1
>j2
102

j
1
j
2
j
1
+j
2
(2 J +1)=(2 j
1
+1)( 2 j
2
+1)
see (6.2.7) where
j
1
=S
and
j
2
=L
These two representations must be physically
equivalent. Each is complete so they are
related by unitary transformations. Thus the
coupled basis function B) can be expanded in
terms of uncoupled ones A) according to

j
1
j
2
J M =

m
1,
m
2
j
1
j
2
m
1
m
2
j
1
j
2
J M j
1
j
2
m
1
m
2

(8.2.1)
Where the expansions coefficients
j
1
j
2
m
1
m
2
j
1
j
2
J M
are called Clebsch-Gordan, or vector
coupling or vector addition or Wigner coefficients.
Fig 18 Vector model for addition of two angular momenta

J
1
and

J
2
to form the resultant

J :
A) in the
1
JM
representation

J
1
and

J
2
precess about

J
B) in the
1
j
1
m
1
,
1
j
2
m
2
representation

J
1
and

J
2
independently precess about the Z axis.
We can write the (8.2.1) in abbreviate form
J M=

m
1,
m
2
j
1
j
2
m
1
m
2
j
1
j
2
J Mm
1
m
2

(8.2.2)
We can use raising and lowering operator and orthogonality to evaluate the coefficients.
J

J =j
1
+j
2,
M=J | J ( J +1)J ( J 1)
1
2
J= j
1
+ j
2,
M=J 1=
=| 2( j
1
+j
2
)
1
2
J = j
1
+ j
2,
M=J 1
(8.2.3)
for the other hand we have that
J

=J
1
+J
2
apply this to the right hand side we have
( J
1
+J
2
)m
1
= j
1,
m
2
=j
2

=| j
1
( j
1
+1)j
1
( j
1
1)
1
2
j
1
1, j
2
+| j
2
( j
2
+1) j
2
( j
2
1)
1
2
j
1,
j
2
1
=| 2 j
1

1
2
j
1
1, j
2
+| 2 j
2

1
2
j
1,
j
2
1
(8.2.4)
Equating right sides of (8.2.3) and (8.2.4) we have:
J = j
1
+ j
2,
M=J1=
(
j
1
j
1
+ j
2
)
1
2
j
1
1, j
2
+
(
j
2
j
1
+ j
2
)
1
2
j
1,
j
2
1 (8.2.5)
103
Fig 18 (a) coupled representation (b) uncoupled
representation see[66]
M
M
m
1
m
1
m
2
m
2
J
2
J
2
J
1
J
1
J J
( a) ( b)
Z Z
The (8.2.5) give us the Clebsch-Gordan coefficients:

j
1
1, j
2
J =j
1
+j
2,
M=J 1=
(
j
1
j
1
+ j
2
)
1
2

j
1
, j
2
1J = j
1
+ j
2,
M=J 1=
(
j
2
j
1
+j
2
)
1
2
(8.2.6)
In [43] pag 269 we have the following notations
C( J
1
J
2
J m
1
m
2
M) J
1
J
2
J MJ
1
m
1
; J
2
m
2

and (8.2.6) become

J
1
J
2
J
1
+J
2
J
1
1 J
2
1 J
1
+J
2
1=
(
j
1
j
1
+ j
2
)
1
2
J
1
J
2
J
1
+J
2
J
1
J
2
1 J
1
+J
2
1=
(
j
2
j
1
+j
2
)
1
2

(8.2.7)
There must be one other J M state with the same value of
M=J 1=j
1
+j
2
1
namely
J = j
1
+ j
2
1 , M=J
. It will have the form
j
1
+j
2
1 , j
1
+ j
2
1=c
1
j
1
1, j
2
+c
2
j
1
, j
2
1
(8.2.8)
But we know that this state must be orthogonal to the
j
1
+j
2
, j
1
+ j
2
1
state, so we require
0= j
1
+ j
2
, j
1
+ j
2
1 j
1
+ j
2
1 , j
1
+ j
2
1
=c
1
(
j
1
j
1
+j
2
)
1
2
+c
2
(
j
2
j
1
+ j
2
)
1
2 (8.2.9)
also normalisation c
1
2
+c
2
2
=1
Hence we find:
c
1
(
j
1
j
1
+ j
2
)
1
2
=c
2
(
j
2
j
1
+j
2
)
1
2
c
1
=c
2
(
j
2
j
1
+j
2

j
1
+ j
2
j
1
)
1
2
c
1
=c
2
(
j
2
j
1
)
1
2
c
1
2
+c
2
2
=1
(
c
2
(
j
2
j
1
)
1
2
)
2
+c
2
2
=1
c
2
2
(
1+
j
2
j
1
)
=1 c
2
=!
.
j
1
j
1
+j
2
thus
104
J = j
1
+ j
2
1 , M=J =
(
j
2
j
1
+j
2
)
1
2
j
1
1, j
2

(
j
1
j
1
+ j
2
)
1
2
j
1,
j
2
1 (8.2.10)
We can continue the process to get lower M values for each of these two vectors.
From (4.2.1) we have that coso=
(
j
1
j
1
+ j
2
)
1
2
and sino=
(
j
2
j
1
+j
2
)
1
2
.
8.3 Examples
This example I have disentangled from [54] pag 386 -390.
We can use (8.2.5) and (8.2.10) or we have step by step:
Consider two particles
j
1
, m
1

and
j
2
, m
2

forming a combined state j , m where

j
1
=1
and
j
2
=1/ 2 1
1
2
. So j can be 1/ 2 or 3/ 2 and
m
max
3/ 2 and 3/ 2 .
You must understand that 1
1
2
is direct product and the basis always will contain
1, x
1
2
, x
see also (6.2.7) and (6.2.8) so J can take only two values J =3/ 2, 1/ 2
J =(1+1/ 2) , (1+1/ 21) , ... ,11/ 2
and for (8.2.3) you see that M=!J
so J M can be only
J =
3
2
, M=+J =
3
2

,
J =
3
2
, M=J =
3
2

and

1
2
,
1
2

1
2
,
1
2

Also the summation rules is valid only for

M=m
1
+m
2
for all basis for example
J M= j
1
m
1
j
2
m
2

so we have two key point for calculating CG coefficients see above:

Coefficients must be normalize to 1
When raising (lowering) a state to an m higher (lower) than J(-J), state =0
we have

3
2
,
3
2
=1, 1
1
2
,
1
2

(8.3.1)

3
2
,
3
2
=1,1
1
2
,
1
2

(8.3.2)
Also

1
2
,
1
2
=1, 0
1
2
,
1
2

1
2
,
1
2
=1, 0
1
2
,
1
2

using definition
105
C
!
=. j ( j+1)m(m!1) (8.3.3)
J

3
2
,
3
2
=1, 1
1
2
,
1
2
=J

1,1
1
2
,
1
2
+1, 1 J

1
2
,
1
2

(8.3.4)
J

3
2
,
3
2
=
.
3
2
(
3
2
+1
)

3
2
(
3
2
1
)

3
2
,
3
2
1
=
.
3
2
(
3
2
+
2
2
)

3
2
(
3
2

2
2
)

3
2
,
1
2
=
.
3
2
(
5
2
)

3
2
(
1
2
)

3
2
,
1
2
=.3
3
2
,
1
2

(8.3.5)
J

1, 1=.1(1+1)1(11)=.21, 11=.21, 0 (8.3.6)

J

1
2
,
1
2
=
.
1
2
(
1
2
+1
)

1
2
(
1
2
1
)

1
2
,
1
2
1
=
.
1
2
(
1
2
+
2
2
)

1
2
(
1
2

2
2
)

1
2
,
1
2
=
.
1
2
(
3
2
)

1
2
(
1
2
)

1
2
,
1
2

=
.
3
4
+
1
4

1
2
,
1
2
=1
1
2
,
1
2

(8.3.7)
Substitution of (8.3.5)(8.3.6)(8.3.7) in (8.3.4) we get
.3
3
2
,
1
2
=.21, 0
1
2
,
1
2
+1,1
1
2
,
1
2

and in final form:

3
2
,
1
2
=
.
2
3
1,0
1
2
,
1
2
+
.
1
3
1, 1
1
2
,
1
2
(8.3.8)
In (8.3.2) we have
m
min
so we act we
J
+

we have
J
+

3
2
,
3
2
=
.
3
2
(
3
2
+1
)

(
3
2
)(
3
2
+1
)

3
2
,
3
2
+1
=
.
3
2
(
3
2
+
2
2
)
+
3
2
(
3
2
+
2
2
)

3
2
,
1
2
=
.
3
2
(
5
2
)
+
3
2
(
1
2
)

3
2
,
1
2
=.3
3
2
,
1
2

J
+
1,1=.1(1+1)(1)(1+1)=.21,1+1=.21, 0
106
J
+

1
2
,
1
2
=
.
1
2
(
1
2
+1
)

1
2
)(

1
2
+1
)

1
2
,
1
2
+1
=
.
1
2
(
1
2
+
2
2
)
+
1
2
(

1
2
+
2
2
)

1
2
,
1
2
=
.
1
2
(
3
2
)
+
1
2
(
1
2
)

1
2
,
1
2

=
.
3
4
+
1
4

1
2
,
1
2
=1
1
2
,
1
2

finally we have

3
2
,
1
2
=
.
2
3
1, 0
1
2
,
1
2
+
.
1
3
1,1
1
2
,
1
2
(8.3.9)
Now taking into account orthogonality (8.2.9) we have the same basis but different CG coefficients

1
2
,
1
2
=c
1
1, 0
1
2
,
1
2
+c
2
1, 1
1
2
,
1
2

see see (8.3.8)

taking into account (8.2.8) we have

1
2,
1
2

3
2
1
2
=0=c
1
.
2
3
+c
2
.
1
3
and c
1
2
+c
2
2
=1 so finally we have (8.2.10) .

1
2
,
1
2
=
.
2
3
1,0
1
2
,
1
2

.
1
3
1, 1
1
2
,
1
2
(8.3.10)
The same procedure for (8.3.9)
we get

1
2
,
1
2
=
.
2
3
1, 0
1
2
,
1
2
+
.
1
3
1,1
1
2
,
1
2
(8.3.11)
OUR CLEBSCH-GORDAN COEFFICIENTS TABLE
1
1
2
j 3
2
3
2
1
2
1
2
3
2
3
2
m
1,
m
2
m 3/ 2 1/ 2 1/ 2 1/ 2 1/ 2 3/ 2
+1 +1/ 2
1
+1 1/ 2 .1/ 3 .2/3
0 +1/ 2 .2/3 .1/3
0 1/ 2 .1/ 3 .2/3
1 +1/ 2 .2/ 3 .1/ 3
1 1/ 2
1
107
Chapter 9 Binomial relationship
9.1 Permutations
Let us first consider a set of n objects that are all different. We may ask in how many ways these n
objects may be arranged, i.e. how many permutations of these objects exist. This is straightforward to
deduce, as follows: the object in the first position may be chosen in n different ways, that in the second
position in n1 ways, and so on until the final object is positioned. The number of possible
arrangements is therefore
n(n1)(n2)...1=n! (9.1.1)
Generalising (9.1.1) slightly, let us suppose we choose only k (< n) objects from n. The number of
possible permutations of these k objects selected from n is given by
108
Illustration 19
taking into account
n(n1)(n2)...( nk+1)(nk)( nk1)...321=n! (9.1.2)
We get:
n(n1)(n2)...( nk+1)=
n!
(nk)!
P
k
n
k factors
n(n1)(n2)...( nk+1)=
n!
(nk)!
P
k
n
(9.1.3)
9.2 Combinations
We now consider the number of combinations of various objects when their order is immaterial.
Assuming all the objects to be distinguishable, from (9.1.3) we see that the number of permutations of
k objects chosen from n is P
k
n
=n!/ (nk)! . Now, since we are no longer concerned with the order
of the chosen objects, which can be internally arranged in k! different ways, the number of
combinations of k objects from n is
n!
( nk )! k !
C
k
n

(
n
k
)
for 0kn (9.2.1)
where, C
k
n
is called the binomial coefficient since it also appears in the binomial expansion for
positive integer n , namely
(a+b)
n
=

k=0
n
C
k
n
a
k
b
nk
(9.2.2)
9.3 Binomial formula
The Binomial Theorem
The Binomial Theorem states that the following binomial formula is valid for all positive integer
values of n:
( a+b)
n
=a
n
+na
n1
b+
n( n1)
2!
a
n2
b
2
+
n( n1) ( n2)
3!
a
n3
b
3
+.. .+b
n
(9.3.1)
The theorem makes it possible to expand finite binomials to any given power without direct
multiplication. The general formula is
109
( a+b)
n
=

k=0
n !
(
n
k
)
a
nk
b
k
(9.3.2)
, which expresses a in descending powers and ( a+b)
n
=

k=0
n!
(
n
k
)
a
k
b
kn
expresses a in ascending
powers. The Theorem also provides a method of determining the binomial coefficients of each term
without having to multiply an expansion out. The n represents the power of the formula and the k
represents the power to which b is raised. Thus,
(
n
k
)
=
n!
k ! ( nk ) !
=C
k
n
(9.3.3)
is the combination formula and is called binomial coefficient. The n! is called the n factorial and
represents the product of the first n positive integers, n! = n (n-1) (n-2) (2) (1). For example, in the
expansion of ( )
5
b a + the coefficient of the third term, a
3
b
2
can be found by using
5!
2! (52) !
=
54321
21321
=
120
12
=10
There are certain properties that the expansions have and are assumed valid where the exponent of
the binomial, (a + b)
n
, is any positive integer. The properties state:
1. The number of terms, in the series, equals the binomial exponent plus one
2. The first term and last term of the series is a
n
and b
n
3. Progressing from the first term to the last, the exponent of a decreases by one from term to
term, the exponent of b increases by one from term to term, and the sum of the exponents of a and b
in each term is n
4. If the coefficient of any term is multiplied by the exponent of a in that term, and this product is
divided by the number of that term, the coefficient of the next term is obtained
5. The coefficients of terms equidistant from the ends are equal.
Pascal Triangle :
n = 0 1
n = 1 1 1
n = 2 1 2 1
n = 3 1 3 3 1
n = 4 1 4 6 4 1

n = n C
0
n
C
1
n
C
n1
n
C
n
n
Example C
1
4
=C
3
4
and C
3
4
=C
3
3
+C
2
3
110
Proof of (9.3.2) by induction:
It is obviously true for n=1,
(a+b)
1
=
1!
0! 1!
a
1
b
0
+
1!
1! 0!
a
0
b
1
=a+b (9.3.4)
Now assume that is true for for n, and consider the next power, n+1
(a+b)
n+1
=(a+b)(a+b)
n
=

k =0
n
(
n
k
)
(a
nk +1
b
k
+a
nk
b
k +1
) (9.3.5)
the exponent sum to n+1 in both terms of the sum. Now rearrange the terms in the sum to the form in
(9.3.2)

l =0
n+1
C
l
a
n+1l
b
l
(9.3.6)
We use here a different summation variable l so that it will not be confused with k in (9.3.5). the
coefficient of the term a
n+1l
b
l
is
C
l
=
(
n
l
)
+
(
n
l 1
)
(9.3.7)
the two terms come from the two terms in (9.3.5). (The first term is the coefficient of a
n+k1
b
k
with
k=l the second term is the coefficient of a
nk
b
k+1
with k=l 1 ).
C
l
can be simplified
using properties of the factorial :
l (l 1)(l 2)...321=l ! l !=(l 1)!l and (nl +1) !=( nl )!( nl +1)
C
l
=
n!
l ! (nl )!
+
n!
(l 1)! (nl +1) !
=
n!
(l 1) !( nl )!
|
1
l
+
1
( nl +1)

=
n!
(l 1) !( nl )!

n+1
l ( n+1l )
=
( n+1) !
(l )! (n+1l )!
=
(
n+l
l
)
i.e.
C
l
is the binomial coefficient for (n+1) factors. Hence (9.3.6) is the formula (9.3.2) in the
theorem for (a+b)
n+1
. So by induction the theorem is proven.
9.4 A relationship among binomial coefficents (Wigner [55] pag 194)
we start from the identity see proof (10.7.11):
111

(
a

)(
b
c
)
=
(
a+b
c
)
(9.4.1)
the left contains the coefficient of x

in (1+x)
a
multiplied by the coefficient of x
c
in
(1+x)
b
and summed over all , that is the coefficient of x
c
in (1+x)
a
(1+x)
b
=
(1+x)
a+b
; and this is the expression on the right side. Let a be a positive integer; b can be negative
or positive. Also for u0 , note that
(
u
v
)
=
u(u1)...( uv+2)( uv+1)
12. ..(v1)v
=(1)
( v)
(vu1)(vu2)...(1u)(u)
12. ..(v1)v
=(1)
v
(
vu1
v
)
128 (9.4.2)
Chapter 10 Explicit formulas for GC or Wigner coefficients
Explicit formulas for GC or Wigner coefficients
10.1 Equivalence between Fock states or coherent states and
spinors
Excited States of the Harmonic Oscillator
see pag 78 [56] we have
a
+

n
( x)=.n+1
n+1
( x) (10.1.1)
or a
+

0
( x)=.0+1
0+1
( x)

n
( x)=
1
.(n)!
( a
+
)
n

0
( x)
(10.1.2)
See pag 129-130 [56] the constructing spin states with larger quantum numbers through spinor
operators
we like to demonstrate, following Jourdan and Schwinger, that states l , m for higher quantum
numbers l =0,
1
2
,1,
3
2
,... , m=l ,l +1,. .. l can be constructed formally from spin states
X
!
if
one considers the two properties
X
!
to be carried by two kinds of bosons, i.e. identical particles any
number of which can exist in the same state
X
+
and
X

. One cannot consider the entities

carrying the spin
1
2
to be particles in the ordinary sense for it can be shown that spin spin
1
2

112
particles have fermion character, i.e. no two such particles can exist in the same state.
Definition of Spinors Creation and Annihilation operators
we present the states
X
!
trough creation operators b
!

which when applied to a formal vacuum

state
1
0

generate
X
!
, i.e.
b
+

1
0
=X
+
; b

1
0
=X

(10.1.3)
The corresponding adjoint operators
b
+
and
b

.
These operators are associated with a given spatial reference system. We consider therefore also
operators of the type
x b

=x
+
b
+

+x

b=x
+

b
+
+x

(10.1.4)
which for x

x=x
+

x
+
+x

=1 represent spinor operators in any arbitrary reference system.

For example using
(d
mm'
1
2
( ))=
(
cos(

2
) sin(

2
)
sin(

2
) cos(

2
) )
the creation operators in a coordinate system rotated by an angle around the y-axis are
(b
+
'
)

=cos

2
b
+

+sin

2
b

(b

'
)

=sin

2
b
+

+cos

2
b

(10.1.5)
The states 1( j , m)
the operators b
!

allow one to construct a set of states which represent j+m fold and j-m fold
X
+

and
X

as follows
1( j , m) =
( b
+

)
j+m
(b

)
j m
.( j +m)! ( jm) !
1
0
(10.1.6)
10.2 Functions of operators
See pag 103 [56] we have
To determine exp A=

+=1

A
+
+!
we split its Taylor expansion into even and odd powers
e
A
=

n=0

1
(2n)!
A
2n
+

n=0

1
(2n+1) !
A
2n+1
(10.2.1)
the property
113
(
0 1
1 0
)
2
=
(
1 0
0 1
)
(10.2.2)
Allows one to write
(
0 1
1 0
)
2n
=(1)
n
(
1 0
0 1
)
,
(
0 1
1 0
)
2n+1
=(1)
n
(
0 1
1 0
)
(10.2.3)
And accordingly
e
A
=

n=0

(1)
n
( 2n) !

2n
(
1 0
0 1
)
+

n=0

(1)
n
( 2n+1) !

2n+1
(
0 1
1 0
)
(10.2.4)
Recognizing the Taylor expansions of cos and sin
e
A
=
(
cos sin
sin cos
)
(10.2.5)
10.3 Generating Function of the States
1( j , m)
We want to prove now the property
exp( x b

)1
0
=

j=0,
1
2
, 1,...

m=j
j

jm
( x) 1( j , m)
(10.3.1)
Where x b

has been defined in (10.1.4) and where

jm
( x)
represents the function of the two
variables
x
+
and
x

closely related to 1( j , m)

jm
( x)=
x
+
j+m
x

j m
.( j+m)! ( j m)!
(10.3.2)
x b

1
0
is called a generating function of 1( j , m) .
In order to derive (10.3.2) we compare the terms

jm
( x)1( j , m)=
( x
+
b
+

)
j+m
( x

)
jm
( j+m)! ( j m)!
1
0
(10.3.3)
With the s-th term in the binomial expansion of (a+b)
n
n!
s !( ns)!
a
ns
b
s
(10.3.4)
Defining
j +m=N s
j m=s
(10.3.5)
We can proof as follows
114

j=0,
1
2
, 1,...

m=j
j

jm
( x)1( j , m) =

j=0,
1
2
, 1,...

1
2j !
( x b

)
2j
1
0

=

u=0,1,. ..

1
u!
( x b

)
u
1
0
=exp( xb

)1
0

(10.3.6)
So

j=0,
1
2
, 1,...

1
2j !
( x b

)
2j
1
0
=

j=0,
1
2
,1,. ..

1
2j !
( x
+
b
+

+x

)
2j
1
0

m=j
j

jm
( x)1( j , m)
(10.3.7)
The summation over s can be written in terms of j and m using (10.3.5)

s=0
N
-

j m=0
2 j
-

m=j
j
(10.3.8)
1
2j !
( x
+
b
+

+x

)
2j
1
0

=
1
N!
( x
+
b
+

+x

)
N
1
0

=
1
N !

s =0
N
|
N!
( Ns)! s !

( x
+
b
+

)
Ns
( x

)
s
(10.3.9)
Finally we get (10.3.3)
1
N !

s=0
N
|
N !
( Ns)! s!

( x
+
b
+

)
Ns
( x

)
s
1
0

=
( x
+
b
+

)
Ns
( x

)
s
( Ns) !( s)!
1
0
=
jm
( x)1( j , m)
(10.3.10)
10.4 Evaluation of the Elements d
mm'
j
() of the Wigner Rotation
Matrix
the spinor algorithm allows one to derive expression for the Wigner rotation matrix elements
d
mm'
j
() . For this purpose se note that the states 1( j , m) in a rotated coordinate system
according to (10.1.6) are
115
1( j , m' ) =
( b'
+

)
j +m'
( b'

)
jm'
.( j+m' ) !( j m' )!
1
0
(10.4.1)
Where (b'
+

) and(b'

) is given by (10.1.5)
on the other side the states 1' ( j , m' ) are related to the states 1( j , m) in the original
coordinate system by
1' ( j , m' ) =d
mm'
j
( )1( j , m) (10.4.2)
Comparison of (10.4.1) and (10.4.2) shows that the elements of the rotation matrix can be obtained by
binomial expansion of b'
+

and b'

in terms of b
+

and b

. For this purpose we expand

(b'
+

)
j+m'
(b'

)
j m'
=( cos

2
b
+

+sin

2
b

)
j+m'
(sin

2
b
+

+cos

2
b

)
jm'
=

c' =0
j+m'

c=0
jm '
(
j +m'
c'
)(
cos

2
)
c'
(
sin

2
)
j+m' +c'
=

c' =0
j+m'

c=0
jm '
(
j m'
c
)(
sin

2
)
c
(
cos

2
)
jm' c
( b
+

)
c' +c
( b

)
2 j c' c
(10.4.3)
The latter sum involves terms (b
+

)
j +m
( b

)
jm
for c' +c= j +m and 2 jc' c= jm . One
may expect that these two conditions restrict both c' and c . However both conditions are satisfied
for c' = j +mc . The combination of c , c' values which yields (b
+

)
j +m
( b

)
jm
is then
c' = j +mc . .The prefactor (b
+

)
j +m
( b

)
jm
which according to (10.4.1) and (10.4.2) can be
identified with the elements d
mm'
j
() of the rotation matrix :
d
mm'
j
()=
.
( j +m) !( j m)!
( j+m' ) !( j m' )!

c=0
jm'
(
j +m'
j+mc
)(
j m'
c
)

(
sin

2
)
2jmm' 2c
(
cos

2
)
m+m' +2c
(10.4.4)
We can expand and to obtain the well known form in spectroscopy
(
j+m'
j +mc
)
=
( j +m' )!
( j +mc) !( j+m' ( j +mc))!
=
( j +m' )!
( j +mc) !( m' m+c)!
(
j m'
c
)
=
( j m' )!
(c)!( j m' c)!
also taking into account that
( j+m' ) !( j m' )!
.( j+m' ) !( j m' )!
=
.
( j+m' ) !( jm' ) !
116
we have
d
mm'
j
()=

c=0
jm'
.( j+m)!( j m) !
( j+mc)!(m' m+c)!
.( j +m' )!( j m' )!
(c)!( jm' c)!

(1)
jm' c
(
sin

2
)
2jmm' 2c
(
cos

2
)
m+m' +2c
(10.4.5)
Also we can made the substitution t = jm' c c= j m' t
2jmm' 2c=2jmm' 2j+2m' +2t=m' m+2t=2tm+m'
m+m' +2c=m' +m+2j2m' 2t =2j+mm' 2t
j +mc= j+m j +m' +t=m+m' +t
m' m+c=m' m+ j m' t =j mt
and obtain
d
mm'
j
()=

t =0
jm'
.( j +m)! ( jm)!
( m+m' +t )! ( jmt )!
.( j+m' ) !( jm' ) !
( j m' t ) ! t !

(1)
t
(
sin

2
)
2tm+m'
(
cos

2
)
2j+mm' 2t
(10.4.6)
10.5 RWF lecture is a notes.pdf from wikipedia
See Chapter 5 (5.2.14)
RWF lecture
Now I can deduce the Wigner deductions of CGC where the integral at pag 191[55] is the beta
functions see my notes on Complex Fourier:
also [60]pag 283:
the deductions of Wigner is in Inui pag 139[71], Tinkham pag 118-122 [73] and Wigner [55] pag 184-
194.
10.5.1 The Beta Function
Using the integral definition(Eq.(5.25)), we write the product of two factorials as the product of two
integrals. To facilitate a change in variables, we take the integrals over a finite range.

m! n! = lim
a
2
-

0
a
2
e
u
u
m
du

0
a
2
e
v
v
n
dv ,

( m)>1,
( n)>1.
(5.57a)
117
Replacing u with x
2
and v with y
2
, we obtain
m! n! =lim
a -
4

0
a
e
x
2
x
2m+1
dx

0
a
e
y
2
y
2n+1
dy.
(5.57b)
Transforming to polar coordinates gives us
m! n! =lim
a -
4

0
a
e
r
2
r
2m+2n+3
dr

0
/2
cos
2m+1
sin
2n+1
d
=( m+n+1)! 2

0
/ 2
cos
2m+1
sin
2n+1
d .
(5.58)
The definite integral, together with the factor 2, has been named the beta function
B( m+1, n+1)2

0
/ 2
cos
2m+1
sin
2n+1
d
=
m! n!
( m+n+1)!
=B( n+1, m+1).
(5.59a)
Equivalently, in terms of the gamma function
B( p , q)=
( p) ( q)
( p+q)
. (5.59b)
Definite integrals, alternative forms
The beta function is useful in the evaluation of a wide variety of definite integrals. The substitution
t=cos
2
converts Eq.(5.59) to
B( m+1, n+1)=
m! n!
( m+n+1)!
=

0
1
t
m
( 1t )
n
dt .
(5.60a)
Replacing t by x
2
, we obtain

m! n!
2( m+n+1)!
=

0
1
x
2m+1
( 1x
2
)
n
dx .
(5.60b)
The substitution t =u/( 1+u) in Eq.(5.60a) yields still another useful form

m! n!
( m+n+1)!
=

u
m
(1+u)
m+n+2
du. (5.61)
Verification of a/sin a = a! (-a)! relation
If we take m= a, n= -a, 0< a < 1, then
118

u
a
(1+u)
2
du=a! (a)! . (5.62)
On the other hand,

u
a
du
( 1+u)
2
=
u
a
1+u

+a

u
a1
du
( 1+u)
=a

e
ax
dx
1+e
x
=
a
sina
.
( u=e
x
)
(the last equality is obtained by using the previous result for the contour integral in Chapter 2).
Therefore, we have proven the relation.
10.6 Explicit expression for Wigner (CG) coefficients I
Explicit expression for Wigner (CG) coefficients
First I found out in the literature I thought that was good see pag 77 [59] but this is not complete and I
have tried to derive and spent many days without nothing.
In [56] and [57] we have the derivation of explicit formula using spinors but is tedious and long and
spinors are more abstract(they have derived the van der varden symetrycal form of wigner coefficent
that is the second form of Racah formulas).
Finally I found another book [60] that is the same as [59] but in detailed explain and contains all
derivations.
From master thesis we have that
.( jm)( j+m+1)=.( j(j ))( j +(j )+1)=.(2j)(1) see (10.6.6):
repeating this procedure m times we have
(

J
+
m
)j =
.
(2j)(1)(2j1)(2)(2j2)(3)...( 2jm+1)(m)m j
=.(2j )(2j1)( 2j2)...( 2jm+1).(1)(2)(3)...( m)m j
=
.
(2j )! m!
(2jm)!
m j
or
m' j =
.
(2jm' )!
( 2j)! m' !
(

J
+
m'
)j (10.6.1)
Making the substitution
m' = jm
119
m=
.
(2jj +m)!
(2j)! ( j m)!
(

J
+
j m
)j =
.
( j +m)!
(2j)! ( j m)!
(

J
+
j m
)j (10.6.2)
or
m=
.
( j+m) !
(2j )!( jm) !
(

J
+
jm
) j (10.6.3)
(10.6.2) Is the same as at pag 77 [59] but and pag 286 [60].
we can generalise (10.6.2) pag 254[60] :
( J

)
k
j , m=

()
k
.
( j +m)!( j m+k )!
( jm)!( j +mk )!
j , mk , k=0,1,... , j+m
0, k= j+m+1, j +m+2,. ..
(10.6.4)
And
( J
+
)
k
j , m=

()
k
.
( j m)! ( j +m+k )!
( j+m)! ( j mk )!
j , m+k , k=0,1,... , j m
0, k= jm+1, j m+2,...
125 (10.6.5)
If we make the substitutions k= j m in (10.6.5) we obtain (10.6.3)
but if we make the same substitution in (10.6.4) we obtain (10.6.2) if we made the assumptions that
m= j and option fro 2j2m=0 and 2m=2j .
We will proof (10.6.5) using the (6.5.11):
J
+
( J
+
j , m)=J
+
(.( j m)( j +m+1) j , m+1)
=
.
( j m)( j +m+1)
.
( j(m+1))( j+( m+1)+1) j , m+2
a
1
b
1
a
2
b
2
122 (10.6.6)
a
n
=( j m)( j m1)( j m2)...( j mk)
b
n
=( j +m+1)( j +m+2)( j +m+3) ...( j +m+k )
in
a
n
the biggest term is j m we will complete the terms on the right in order to obtain factorial
in
b
n
the biggest term is j +m+k we will complete the range on the left
so we have:
( j m)( j m1)( j m2)... ( j mk)...
( j3)( j2)( j 1)
( j3)( j2)( j 1)
=
( j m)!
( jmk )!
and
the same to the left
( j+1)( j +2)( j+3)... ( j +m)
( j+1)( j +2)( j+3)... ( j +m)
( j+m+1)( j +m+2)( j+m+3)...( j+m+k)=
( j+m+k)!
( j +m)!
which was to be proved.
120
10.6.1 Explicit expression for Clebsch-Gordan coefficients (CGC) (Wigner's formula)II
We consider the angular momentum operator see pag 275 [60]:
J =J
1
+J
2
(10.6.7)
we have for
( J
1
, J
2
)
system
j
1
, m
1
j
2
, m
2
j
1
, m
1
; j
2
, m
2
m
1
, m
2

(10.6.8)
For the combined system we note their simultaneously eigenstates by
j , m; j
1
, j
2
j , m
(10.6.9)
For a given fixed pair
( j
1
, j
2
)
we may expand the eigenstates j , m in (10.6.9) in the terms of
the basis
{m
1
, m
2
}
in (10.6.8):
j , m=

m
1
, m
2
m
1
, m
2
m
1
, m
2
j , m
(10.6.10)
We may revert (10.6.10) and expand
m
1
, m
2

in terms of j , m
m
1
, m
2
=

j=j
1
j
2

j=j
1
+ j
2

j , m m
1
, m
2
m
1
, m
2

where
m=m
1
+m
2
From the orthonormality relations
j ' , m' j , m=6
j ' , j
6
m' , m
(10.6.11)
m
1
'
m
2
'
m
1
, m
2
=6
m
1
'
,m
1
6
m
2
'
, m
2
(10.6.12)
Upon applying
J
!
=J
1!
+J
2!
(10.6.13)
To (10.6.10) and using (6.5.11) we obtain
.( jm)( j!m+1) j , m!1
=

m
1
,m
2
.
( j
1
m
1
)( j
1
!m
1
+1)m
1
!1 , m
2
m
1
, m
2
j , m
+

m
1
, m
2
.
( j
2
m
2
)( j
2
!m
2
+1)m
1
, m
2
!1 m
1
, m
2
j , m
(10.6.14)
Which upon multiplying by m
1
'
m
2
'
and using (10.6.12) gives the following useful relationship CG
coefficients :
121
.( jm)( j!m+1) m
1
, m
2
j , m!1
=

m
1
,m
2
.
( j
1
m
1
)( j
1
!m
1
+1) m
1
!1, m
2
j , m
+

m
1
, m
2
.
( j
2
m
2
)( j
2
!m
2
+1) m
1
, m
2
!1 j , m
(10.6.15)
To obtain the explicit expression for the CGC for the addition of two angular momenta we may proceed
as follows. Taking the upper sign in the recurrence relation (10.6.15) with m= j ,
m
2
=j +1m
1
,its left hand side is then zero and leads to
.
( j
1
+m
1
)( j
1
m
1
+1) m
1
1, m
2
j , j
=
.
( j
2
+m
2
)( j
2
m
2
+1) m
1
, m
2
1 j , j
(10.6.16)
By successive replacements
m
1
-m
1
+1-m
1
+2,. .. , j
and
m
2
=j +1m
1
we get the following
chain of equations(see the procedure of (10.6.6)):
m
1
, j m
1
j , j =
.
( j
2
+j m
1
)( j
2
j+m
1
+1)
( j
1
+m
1
+1)( j
1
m
1
)
m
1
+1, j m
1
1 j , j

m
1
+1, jm
1
1 j , j =
.
( j
2
+ jm
1
1)( j
2
j +m
1
+2)
( j
1
+m
1
+2)( j
1
m
1
1)
m
1
+2, j m
1
2 j , j

j
1
1, j j
1
+1 j , j =
.
( j
2
+ j j
1
+1)( j
2
j +j
1
)
( 2j
1
)
j
1
, j j
1
j , j
(10.6.17)
Upon taking the product of this quantities we have from first equation of (10.6.17): we begin with
numerator and finish with denominators:
( j
2
+ jm
1
)( j
2
+ jm
1
1) ...( j
2
+ j j
1
+1)=(decrease j
2
> j
1
)=
( j
2
+ j m
1
) !
( j
2
+ j j
1
)!
(10.6.18)
( j
2
j+m
1
+1)( j
2
j +m
1
+2) ...( j
2
j+ j
1
)=
( j
2
j+ j
1
)!
( j
2
j+m
1
) !
(10.6.19)
For denominators
( j
1
m
1
)( j
1
m
1
1) ...( j
1
j
1
)=( j
1
m
1
) ...10=( j
1
m
1
)!
(10.6.20)
And
( j
1
+m
1
+1)( j
1
+m
1
+2) ...( j
1
+j
1
)=
012...( j
1
+m
1
)( j
1
+m
1
+1) ...2j
1
=
( 2j
1
)!
( j
1
+m
1
)!
(10.6.21)
122
Substituting (10.6.18),(10.6.19),(10.6.20) and (10.6.21) in product of of (10.6.17):
m
1
, j m
1
j , j =(1)
j
1
m
1

.
( j
2
+j m
1
)!
( j
2
+ j j
1
)!
.
( j
2
j +j
1
)!
( j
2
j +m
1
)!
.
1
( j
1
m
1
)!
.
( j
1
+m
1
) !
(2j
1
) !
j
1
, j j
1
j , j
(10.6.22)
This can be rearranged as:
m
1
, j m
1
j , j =

(1)
j
1
m
1
.
(2j
1
) ! .
( j
2
j +j
1
)!
( j
2
+ j j
1
)!
.
( j
1
+m
1
) ! ( j
2
+ jm
1
)!
( j
1
m
1
) ! ( j
2
j +m
1
)!
j
1
, j j
1
j , j
(10.6.23)
To obtain the expression for
j
1
, j j
1
j , j
, we use the unitary condition:

m
1
+m
2
= j
m
1
, j m
1
j , j
2
=1
(10.6.24)
And the sum:

m
1
+m
2
= j .
( j
1
+m
1
)! ( j
2
+ jm
1
)!
( j
1
m
1
)! ( j
2
j+m
1
)!
=

m
1
+m
2
= j .
( j
1
+m
1
)! ( j
2
+m
2
)!
( j
1
m
1
)! ( j
2
m
2
)!
=
( j+ j
1
+ j
2
+1) ! ( j
2
j
1
+ j )! ( j
1
j
2
+ j )!
(2j+1)! ( j
1
+ j
2
j )!
124, 125, 127 (10.6.25)
Where I used
m
1
+m
2
=j
after substitution we get
j
2
+ jm
1
=j
2
+m
1
+m
2
m
1
=j
2
+m
2
.
Thus
1
j
1
, j j
1
j , j
=
1
.
( 2j
1
)! .
( j
2
j +j
1
)!
( j
2
+ j j
1
)!

m
1
+m
2
= j .
( j
1
+m
1
) ! ( j
2
+ jm
1
)!
( j
1
m
1
) ! ( j
2
j+m
1
)!
=
1
.
(2j
1
) ! .
( j
2
j+ j
1
)!
( j
2
+ j j
1
)!
.
( j+ j
1
+ j
2
+1)! ( j
2
j
1
+ j )! ( j
1
j
2
+ j )!
(2j+1)! ( j
1
+ j
2
j )!
=
1
.
(2j
1
)! .
( j +j
1
+j
2
+1)! ( j
1
j
2
+j )!
(2j+1) !
or
j
1
, j j
1
j , j =
.
( 2j
1
)! (2j+1)!
( j+ j
1
+ j
2
+1)! ( j
1
j
2
+ j )!
(10.6.26)
Substituting (10.6.26) in (10.6.23) we obtain:
123
m
1
, j m
1
j , j =(1)
j
1
m
1

.
( 2j+1)!
( j+ j
1
+ j
2
+1)! ( j
1
j
2
+ j )!
.
( j
2
j +j
1
) !
( j
2
+j j
1
) !
.
( j
1
+m
1
)! ( j
2
+ jm
1
)!
( j
1
m
1
)! ( j
2
j+m
1
)!
(10.6.27)
By making the substitution
j
1
m
1
= j
1
m
1
k
=
m
1
=m
1
k
in (10.6.27) we get:
m
1
, j m
1
j , j =(1)
j
1
m
1
k

.
( 2j+1)!
( j+ j
1
+ j
2
+1)! ( j
1
j
2
+ j )!
.
( j
2
j +j
1
) !
( j
2
+j j
1
) !
.
( j
1
+m
1
+k)! ( j
2
+j m
1
k) !
( j
1
m
1
k)! ( j
2
j +m
1
+k) !
127 (10.6.28)
By making the substitution
m
1
=m
1
+k
in (10.6.27) we get:
m
1
, j m
1
j , j =(1)
j
1
m
1
k

.
( 2j+1)!
( j+ j
1
+ j
2
+1)! ( j
1
j
2
+ j )!
.
( j
2
j +j
1
) !
( j
2
+j j
1
) !
.
( j
1
+m
1
k)! ( j
2
+j m
1
+k) !
( j
1
m
1
+k)! ( j
2
j +m
1
k) !
Now we will proof the identity (10.6.25):
( x+y)
a
=

k
1
=0

(1)
k
1
y
k
1
x
ak
1
k
1
!
( a+k
1
1) !
(a1)!
( x+y)
b
=

k
1
=0

(1)
k
2
y
k
2
x
bk
2
k
2
!
(b+k
2
1) !
(b1) !
and ( x+y)
( a+b)
=

k =0

(1)
k y
k
x
( a+b)k
k !
((a+b)+k1)!
(a+b1)!
taking into account that ( x+y)
a
( x+y)
b
=( x+y)
(a+b)
we get for proof see (10.7.11)

k
1
+k
2
=k
(a+k
2
1) !
(a1)!
( b+k
2
1)!
(b1)! k
1
! k
2
!
=
(a+b+k1)!
(a+b1)! k !
(10.6.29)
Upon settings
k
1
= j
1
m
1
,
k
2
=j
2
m
2
and
a1= j
2
j
1
+j
,
b1= j
1
j
2
+j
thus we get
k
1
+k
2
=k=j
1
m
1
+ j
2
m
2
= j
1
+ j
2
+ j

where
j =m
1
+m
2
(10.6.30)
Substituting in LHS of (10.6.29):
124
(a+k
2
1)!
(a1)!
(b+k
2
1)!
( b1)! k
1
! k
2
!
=
( j
2
j
1
+ j+ j
1
m
1
)! ( j
1
j
2
+j + j
2
m
2
1)!
( j
2
j
1
+ j )! ( j
1
j
2
+ j )! ( j
1
m
1
)! ( j
2
m
2
)!
=
( j
2
+j m
1
)! ( j
1
+ jm
2
) !
( j
2
j
1
+j ) ! ( j
1
j
2
+ j )! ( j
1
m
1
)! ( j
2
m
2
) !
=
( j
2
+m
2
)! ( j
1
+m
1
)!
( j
2
j
1
+ j )! ( j
1
j
2
+j ) ! ( j
1
m
1
) ! ( j
2
m
2
)!
(10.6.31)
for the RHS of (10.6.29):
(a+b+k1)!
( a+b1)! k !
=
( j
2
j
1
+j +1+ j
1
j
2
+ j +1+ j
1
+ j
2
j 1)!
( j
2
j
1
+ j+1+j
1
j
2
+ j+11)! ( j
1
+j
2
+ j )!
=
( j + j
1
+ j
2
+1) !
(2j+1)! ( j
1
+j
2
j )!
(10.6.32)
Equating (10.6.31) and (10.6.32) we get (10.6.25).
10.7 Explicit expression for Clebsch-Gordan coefficients (CGC)
(Wigner's formula)III
To obtain the expression for the general coefficient
m
1,
m
2
j , m
we note from (10.6.5) that by
substitution k= j m we get (see for example [59] pag 78 )
j , m=
.
( j +m)!
2j ! ( j m)!
1
()
jm
( J
+
)
jm
j , j (10.7.1)
By decomposition
j , j =

m
1
= j
1
j
1
m
1,
j m
1
m
1,
j m
1
j , j (10.7.2)
And hence amounts to evaluating
.
( j+m)!
2j ! ( jm)!
1
()
j m
m
1,
j m
1
( J
+
)
j m
j , j =

m
1
=j
1
j
1
.
( j +m)!
2j ! ( j m)!
1
()
j m
m
1,
j m
1
( J
+
)
j m
m
1,
j m
1
m
1,
jm
1
j , j =
m
1,
jm
1
j , m
(10.7.3)
We use the binomial expansion
125
( J
+
)
j m
=

k=0
j m
(
j m
k
)
( J
1+
)
k
( J
2+
)
j mk
(10.7.4)
Where
(
j m
k
)
=
( j m)!
k ! ( j mk) !
(10.7.5)
From (10.6.5) we have :
( J
1+
)
k
j
1,
m
1
=
.
( j
1
m
1
) !( j
1
+m
1
+k) !
( j
1
+m
1
) !( j
1
m
1
k) !
j
1,
m
1
+k (10.7.6)
And
( J
2+
)
j mk
j
2,
m
2
=
.
( j
2
m
2
)!( j
2
+m
2
+ j mk)!
( j
2
+m
2
)!( j
2
m
2
j+m+k)!
j
2,
m
2
+ j m+k (10.7.7)
Substituting (10.7.5),(10.7.6),(10.7.7)in(10.7.3) :
m
1,
j m
1
j , m=

m
1
=j
1
j
1
.
( j +m)!
2j ! ( j m)!
1
()
j m
m
1,
j m
1
( J
+
)
j m
m
1,
j m
1
m
1,
jm
1
j , j =

m
1
+m
2
= j

k
.
( j +m)!
2j ! ( j m)!
( )
j m
( )
jm
( jm)!
k ! ( j mk) !

.
( j
1
m
1
)! ( j
1
+m
1
+k)!
( j
1
+m
1
)! ( j
1
m
1
k)!
m
1
m
1
+k

.
( j
2
m
2
)! ( j
2
+m
2
+ jmk )!
( j
2
+m
2
)! ( j
2
m
2
j+m+k )!
j m
1
m
2
+ jm+k m
1,
j m
1
j , j
(10.7.8)
we made the substitutions
m
2
m=m
1
and
m
2
+m=m
1
for

k =0
m
1
m
1
+k =1
and
jm
1
m
2
+j m+k = jm
1
j m
1
+k =1
we get
126
m
1,
jm
1
j , m=

k .
( j +m)!
2j ! ( j m)!
( jm) !
k ! ( j mk) !

.
( j
1
m
1
)! ( j
1
+m
1
+k) !
( j
1
+m
1
)! ( j
1
m
1
k) !

.
( j
2
m
2
)! ( j
2
+j m
1
k)!
( j
2
+m
2
)! ( j
2
j +m
1
+k)!
m
1,
j m
1
j , j
(10.7.9)
Thus substituting (10.6.28) in (10.7.9) and taking into account that
.
(2j+1)!
2j !
=.2j+1 and
( jm)!
.( j m)!
=.( j m)!
we finallyyyyyyyy get :
m
1,
m
2
j , m= j
1
j
2
m
1,
m
2
j
1
j
2
j m=m
1,
j m
1
j , m=
.2j+1
.
( j m)! ( j+m) !
( j+ j
1
+ j
2
+1)! ( j
1
j
2
+ j )!
.
( j
2
j +j
1
) !
( j
2
+j j
1
) !

.
( j
1
m
1
)! ( j
2
m
2
)!
( j
1
+m
1
)! ( j
2
+m
2
) !

k
(1)
j
1
m
1
k
k ! ( j mk )!
( j
1
+m
1
+k )! ( j
2
+ jm
1
k )!
( j
1
m
1
k )! ( j
2
j+m
1
+k )!
128,130 (10.7.10)
In Racah [81]and [59] pag 79 we have (1)
j
1
m
1
+k
but in in Judd [82]pag 12, pag 287 [60]we have
(1)
j
1
m
1
k
in Griffith[83] pag 22 is the same as pag 287 [60] but is not correct to apply
J

on j , m
because we will not obtain
.
( j
1
m
1
)! ( j
2
m
2
)!
( j
1
+m
1
)! ( j
2
+m
2
)!
only with
J
+
on j , m see pag 78[59].
also from (10.7.4) we have ( J )
j mk
and the (10.6.25) is correct as in Judd [82]pag 11 and [59] pag
77. And I also have verified diligently.
The true is that (1)
j
1
m
1
k
is correct see [84] pag 45:where he check the Racah[81] formulas (16-
17').
10.7.1 Van der Waerden symmetric form of CGC
I taked from Magnet.odt
see Griffith [83]pag 21:
Vandermondes Theorem:
C
r
m+n
=C
r
m
+C
r1
m
C
1
n
+C
r2
m
C
2
n
++C
rs
m
C
s
n
++C
r
n
.
May be written as

+ +

+ +

+
r
n
s
n
s r
m n
r
m n
r
m
r
m
r
n m

2 2 1 1
.
or
127
(
m+n
r
)
=

s
(
m
rs
)(
n
s
)
124 ,111 (10.7.11)
PROOF
( 1+x)
m+n
=1+C
1
m+n
x+C
2
m+n
x
2
++C
r
m+n
x
r
++x
m+n
.
On the other hand,
( 1+x)
m+n
=( 1+x)
m
( 1+x)
n
=
(
1+C
1
m
x+C
2
m
x
2
++C
r
m
x
r
++x
m
) (
1+C
1
n
x+C
2
n
x
2
++C
r
n
x
r
++x
n
)
Equating the coefficient of x
r
, C
r
m+n
=C
r
m
+C
r1
m
C
1
n
+C
r2
m
C
2
n
++C
rs
m
C
s
n
++C
r
n
.
see Griffith [83]pag 21:thus we had multiplied term by term and equate the coefficients of x
r
.
see Racah [80]formula (52)-(55)
putting n=ab , m=b , r=ac in(10.7.11): we have
a!
b! c!
=

s
(ab)! (ac)!
(abs )! (acs)! (b+ca+s)! s!
(10.7.12)
See eq(9.4.2):
if m is negative we can transform (10.7.11):by means of
(
m
rs
)
=(1)
r s
(
rsm1
rs
)
(10.7.13)
And obtain
(
rnm1
r
)
=

s
(1)
s
(
rsm1
rs
)(
n
s
)
(10.7.14)
Putting m=rt 1 we have from (10.7.14):

s
(1)
s
(t s)!
s ! (ns)! (rs )!
=
(t n)! (t r )!
n! r ! (t nr ) !
(10.7.15)
See Racah formula (15) and (16) [81]: using (10.7.12), (10.7.15) in the last part of (10.7.10):

k
(1)
j
1
m
1
k
k ! ( j mk) !
( j
1
+m
1
+k) ! ( j
2
+ jm
1
k )!
( j
1
m
1
k) ! ( j
2
j+m
1
+k )!
=

k
(1)
j
1
m
1
k
( j
1
+m
1
+k )!
k ! ( j
2
j +m
1
+k)!
( j
2
+j m
1
k) !
( jmk)! ( j
1
m
1
k )!
(10.7.16)
128
( j
2
+j m
1
k)!
( jmk )! ( j
1
m
1
k) !
=
a!
b! c!

u
( ab)! (ac)!
( abu)!(acu)!( b+ca+u) ! u!
=

u
( j
2
+j m
1
kj +m+k )!( j
2
+ j m
1
k j
1
+m
1
+k)!
( j
2
m
1
+mu)!( j +j
2
j
1
u) ! ( j mk+ j
1
m
1
k j
2
+ j m
1
k+u)! u!
=

u
( j
2
m
1
+m)! ( j+ j
2
j
1
)!
( j
2
m
1
+mu)! ( j +j
2
j
1
u)!( j
1
j
2
mk+u)! u!

u
( j
2
+m
2
)!( j+ j
2
j
1
)!
( j
2
+m
2
u) !( j +j
2
j
1
u)!( j
1
j
2
mk+u)! u!
thus (10.7.16) become:

k
(1)
j
1
m
1
k
( j
1
+m
1
+k) !
k ! ( j
2
j+m
1
+k )!
( j
2
+ j m
1
k)!
( j mk )! ( j
1
m
1
k)!
=

ku
(1)
j
1
m
1
k
( j
1
+m
1
+k) !
k ! ( j
2
j+m
1
+k )!
( j
2
+m
2
) ! ( j +j
2
j
1
)!
( j
2
+m
2
u)! ( j+ j
2
j
1
u)! ( j
1
j
2
mk+u) ! u!
(10.7.17)
Now using (10.7.15) in (10.7.17) for the chosen terms:

k u
(1)
j
1
m
1
k
( j
1
+m
1
+k) !
k ! ( j
2
j+m
1
+k )!
1
( j
1
j
2
mk+u)!
(10.7.18)
we will get rid of t in LHS of k because k are in all 4 terms

k u
(1)
j
1
m
1
k
( j
1
+m
1
+k) !
k ! ( j
2
j+m
1
+k )!
1
( j
1
j
2
mk+u)!
=

s
(1)
s
(t s )!
s! (ns) ! (rs)!
we made the transformations in order to have the same like in RHS:

k u
(1)
j
1
m
1
k
( j
1
+m
1
+2kk)!
k ! ( j
2
j+m
1
+2kk )!
1
( j
1
j
2
m+uk)!
=

s
(1)
s
(t s)!
s ! (ns)! ( rs)!
(10.7.19)
thus
t =j
1
+m
1
+2k

n=j
2
j+m
1
+2k
r=j
1
j
2
m+u
(10.7.20)
Substituting (10.7.20) in RHS of (10.7.15):
(tn)! (t r)!
n! r ! (t nr )!
=
( j
1
+m
1
+2kj
2
+ jm
1
2k)! ( j
1
+m
1
+2k j
1
+ j
2
+mu) !
( j
2
j +m
1
+2k)! ( j
1
j
2
m+u) !

1
( j
1
+m
1
+2k j
2
+j m
1
2k j
1
+ j
2
+mu)!
=
( j
1
j
2
+ j )! (m
1
+2k+ j
2
+mu)!
( j
2
j +m
1
+2k) ! ( j
1
j
2
m+u)!
1
( j +mu)!
129
thus (10.7.19) become:

k u
(1)
j
1
m
1
k
( j
1
+m
1
+2kk)!
k ! ( j
2
j+m
1
+2kk )!
1
( j
1
j
2
m+uk)!
=

k u
(1)
j
1
m
1
k
( j
1
j
2
+ j )! (m
1
+2k+ j
2
+mu) !
( j
2
j+m
1
+2k)! ( j
1
j
2
m+u) !
1
( j +mu)!
now substituting
k+ j
2
+m
2
u=j
1
m
1
k
m
1
+2k+ j
2
+mu=2m
1
+k+( k+j
2
+m
2
u)=2m
1
+k+( j
1
m
1
k )= j
1
+m
1
j
2
j+m
1
+2k=( k+j
2
+m
2
u)m
2
+u j+m
1
+k
=( j
1
m
1
k)m
2
+u j+m
1
+k= j
1
jm
2
+u

k u
(1)
j
1
m
1
k
( j
1
j
2
+j ) ! (m
1
+2k+j
2
+mu)!
( j
2
j +m
1
+2k)! ( j
1
j
2
m+u)!
1
( j +mu)!
=

u
(1)
j
2
+m
2
u+k
( j
1
j
2
+j ) !( j
1
+m
1
) !
( j
1
jm
2
+u)!( j
1
j
2
m+u) !
1
( j +mu)!
now we made the substitution
j
2
+m
2
u+k=j
2
+m
2
u
we see that nothing is changed because we
don't have the k at numerator and denominator :

u
(1)
j
2
+m
2
u+k
( j
1
j
2
+ j )! ( j
1
+m
1
)!
( j
1
j m
2
+u)! ( j
1
j
2
m+u)!
1
( j+mu) !
=

u
(1)
j
2
+m
2
u
( j
1
j
2
+j ) ! ( j
1
+m
1
) !
( j
1
jm
2
+u)! ( j
1
j
2
m+u) !
1
( j +mu)!
(10.7.21)
Substituting (10.7.21)=(10.7.18) in (10.7.17) finally we get:

k
(1)
j
1
m
1
k
( j
1
+m
1
+k)!
k ! ( j
2
j +m
1
+k )!
( j
2
+ jm
1
k )!
( j mk) ! ( j
1
m
1
k)!
=

ku
(1)
j
1
m
1
k
( j
1
+m
1
+k) !
k ! ( j
2
j+m
1
+k )!
( j
2
+m
2
) ! ( j +j
2
j
1
)!
( j
2
+m
2
u)! ( j+ j
2
j
1
u)! ( j
1
j
2
mk+u) ! u!
=

u
(1)
j
2
+m
2
u
( j
1
j
2
+j ) ! ( j
1
+m
1
) !
( j
1
j m
2
+u)! ( j
1
j
2
m+u) !
1
( j +mu)!

( j
2
+m
2
)! ( j+ j
2
j
1
)!
( j
2
+m
2
u)! ( j+ j
2
j
1
u)! u!
(10.7.22)
Finally putting
z=j
2
+m
2
u
(10.7.22) and all in (10.7.10) we get the symmetric form van der
Waerden that Racah was able to bring see [59]pag 79:
j
1
j
2
m
1
m
2
j
1
j
2
j m=6(m
1
+m
2,
m)
|
(2j+1)( j
1
+j
2
j )! ( j + j
1
j
2
)! ( j+ j
2
j
1
)!
( j
1
+j
2
+ j+1)!

1
2

z
(1)
z
.
( j
1
+m
1
)! ( j
1
m
1
)! ( j
2
+m
2
)! ( j
2
m
2
) ! ( j +m)! ( jm) !
z ! ( j
1
+ j
2
j z)! ( j
1
m
1
z)! ( j
2
+m
2
z)! ( j j
2
+m
1
+z) ! ( j j
1
m
2
+z)!
(10.7.23)
You can see (10.7.23) in [56]pag 158 ,[57],[58] pag ,[59] pag 79.
130
10.7.2 Wigner 3j symbols or Racah formula
It is convenient to introduce the abbreviations:
See Racah formula (17),(17') and (16') [81]:
V (ab c; o)=
(
a b c
o
)
=

z
(1)
( c+z)

.
(A(abc))
.(( a+o) ! (ao)! (b+)! ( b) ! (c+)! ( c)! )
z! ( a+bcz)! ( aoz)! ( b+z)! (cb+o+z)! (co+z) !
(10.7.24)
Where V ( abc ; o) is the Racah V-coefficient and
A( abc)=
((a+bc)! (ab+c)! (a+b+c)! )
(( a+b+c+1)! )
,
and finally for CGC:(=(10.7.23))
j
1
j
2
m
1
m
2
j
1
j
2
j m=(1)
j+m
.2j+1V ( j
1
j
2
jm
1
m
2
m) (10.7.25)
Thus putting (10.7.24) in (10.7.25) (10.7.23):
(1)
(c+z)
=(1)
( jm+z)
(1)
j+m
(1)
jm+z
=(1)
z

(10.7.23).
The same for 3j symbols
at pag 290 [55] he introduce his 3j symbols that is in terms of his deduction CGC:
(
j
1
j
2
j
m
1
m
2
m
)
=(1)
j
1
j
2
m 1
.2j+1
j
1
m
1
j
2
m
2
jm
(10.7.26)
Where (se pag 140[71]):
A( j
1
j
2
j )=
.
( j
1
+j
2
j )! ( j+ j
1
j
2
)! ( j +j
2
j
1
) !
( j
1
+ j
2
+j +1)!
(
j
1
j
2
j
3
m
1
m
2
m
3
)
=6(m
1
+m
2,
m)
.
( j
1
+j
2
j )!( j+ j
1
j
2
)! ( j+ j
2
j
1
)!
( j
1
+ j
2
+j +1)!

z
(1)
j
1
j
2
m+z .
( j
1
+m
1
)!( j
1
m
1
)!( j
2
+m
2
)!( j
2
m
2
) ! ( j +m)! ( jm)!
z !( j
1
+ j
2
j z)! ( j
1
m
1
z)! ( j
2
+m
2
z)!( j j
2
+m
1
+z) ! ( j j
1
m
2
+z)!
=6( m
1
+m
2,
m)A( j
1
j
2
j )

z
(1)
j
1
j
2
m+z .
( j
1
+m
1
)!( j
1
m
1
)!( j
2
+m
2
)!( j
2
m
2
) ! ( j +m)! ( jm)!
z !( j
1
+ j
2
j z)! ( j
1
m
1
z)! ( j
2
+m
2
z)!( j j
2
+m
1
+z) ! ( j j
1
m
2
+z)!
substituting the last equation in (10.7.26):
131
(1)
j
1
j
2
m+z
(1)
j
1
+ j
2
+m
=(1)
z
and we obtain (10.7.23).
Wigner:
V ( abc ; o)=(1)
a+bc
V (ba c ; o )=(1)
a+b+c
V ( acb ; o)=
(1)
2b
V ( ca b; o)=(1)
2c
V (b ca ; o)
(10.7.27)
interchanging in (10.7.24) a with b and o with
V ( abc ; o)=(1)
2
V (b ac ;o) (10.7.28)
And owing to the first (10.7.27) and the fact that 2(c) is even , we get also:
V ( abc ; o)=(1)
a+b+c
V (ab c ;o) (10.7.29)
See [73] pag 122: V are related to CGC(by the reversion of (10.7.25)):
V ( j
1
j
2
j
3
, m
1
m
2
m
3
)=(1)
j
3
m
3
1
.
2j
3
+1
A
m
1
m
2
m
3
j
1
j
2
j
3
=(1)
j
3
m
3
1
.
2j
3
+1
j
1
j
2
m
1
m
2
j
1
j
2
j
3
m
3

=(1)
j
3
m
3
1
.
2j
3
+1
j
1
m
1
j
2
m
2
j
3
m
3

(10.7.30)
Wigner introduced his so called 3j- symbol which is related to the coefficients V by a simple phase
change, namely
(
j
1
j
2
j
3
m
1
m
2
m
3
)
=(1)
j
3
+ j
2
j
1
V ( j
1
j
2
j
3
, m
1
m
2
m
3
)
(10.7.31)
If you have a look in (10.7.27) we dont have a phase with (1)
a+b+c
. And pag 123[73] V
coefficients are less symmetric than 3j.
Thus the 3j symbol can be calculated using Racah formula (10.7.24) (see
http://mathworld.wolfram.com/Wigner3j-Symbol.html).
In http://en.citizendium.org/wiki/3j-symbol and
(http://en.wikipedia.org/wiki/Clebsch_Gordan_coefficients) we have
132
j
1
m
1
j
2
m
2
j
3
m
3
=(1)
j
1
j
2
m
3
.
2j
3
+1
(
j
1
j
2
j
3
m
1
m
2
m
3
)
(10.7.32)
proof: by substituting (10.7.31)in(10.7.32)
we get
j
1
m
1
j
2
m
2
j
3
m
3
=(1)
j
1
j
2
m
3
(1)
j
3
+ j
2
j
1
.
2j
3
+1V ( j
1
j
2
j
3
, m
1
m
2
m
3
)
j
1
m
1
j
2
m
2
j
3
m
3
=(1)
j
3
m
3
.
2j
3
+1V ( j
1
j
2
j
3
, m
1
m
2
m
3
)
j
1
m
1
j
2
m
2
j
3
m
3
=(1)
j
3
+m
3
.
2j
3
+1V ( j
1
j
2
j
3
, m
1
m
2
m
3
)
(10.7.33)
Which is equivalent with (10.7.25).
but in http://en.wikipedia.org/wiki/Wigner_3-j_symbols and Sobelman[85] pag 61 we have different
phase phactor!!!:
j
1
m
1
j
2
m
2
j
3
m
3
=(1)
j
1
+j
2
m
3
.
2j
3
+1
(
j
1
j
2
j
3
m
1
m
2
m
3
)

(1)
j
1
j
2
+m
3
1
.
2j
3
+1
j
1
m
1
j
2
m
2
j
3
m
3
=
(
j
1
j
2
j
3
m
1
m
2
m
3
)
Proof of (10.7.36)
and changing
m
3
with
m
3
(1)
j
1
j
2
m
3
1
.
2j
3
+1
j
1
m
1
j
2
m
2
j
3
m
3
=
(
j
1
j
2
j
3
m
1
m
2
m
3
)
(10.7.34)
proof: by substituting (10.7.31)in (10.7.34)
we get
j
1
m
1
j
2
m
2
j
3
m
3
=(1)
j
1
+j
2
m
3
.
2j
3
+1
(
j
1
j
2
j
3
m
1
m
2
m
3
)

j
1
m
1
j
2
m
2
j
3
m
3
=(1)
j
1
+j
2
m
3
(1)
j
3
+ j
2
j
1
.
2j
3
+1V ( j
1
j
2
j
3
, m
1
m
2
m
3
)
j
1
m
1
j
2
m
2
j
3
m
3
=(1)
j
3
m
3
2j
1
+2j
2
.
2j
3
+1V ( j
1
j
2
j
3
, m
1
m
2
m
3
)
and
(1)
2j
1
+2j
2
=((1)
j
1
)
2
( (1)
j
2
)
2
=
(
1
(1)
j
1
)
2
( (1)
j
2
)
2
=11
because we have even numbers (1)
2
=1 thus
j
1
m
1
j
2
m
2
j
3
m
3
=(1)
j
3
m
3
.
2j
3
+1V ( j
1
j
2
j
3
, m
1
m
2
m
3
) and
j
1
m
1
j
2
m
2
j
3
m
3
=(1)
j
3
+m
3
.
2j
3
+1V ( j
1
j
2
j
3
, m
1
m
2
m
3
)
(10.7.35)
133
The inverse see [18] pag 544:and See (http://en.wikipedia.org/wiki/Clebsch_Gordan_coefficients)
(
j
1
j
2
j
3
m
1
m
2
m
3
)
=(1)
j
1
j
2
m
3
1
.
2j
3
+1
j
1
m
1
j
2
m
2
j
3
m
3

(10.7.36)
(1)
j
1
j
2
m
3
phase factor (10.7.37)
1
.
2j
3
+1
weight factor see pag 544 [18] (10.7.38)
Proof by substituting RHS of (10.7.31)in (10.7.36) we get(10.7.30)(by taking into account(10.7.35) or
pag 61[85])
(
j
1
j
2
j
3
m
1
m
2
m
3
)
=(1)
j
1
j
2
m
3
1
.
2j
3
+1
j
1
m
1
j
2
m
2
j
3
m
3

(1)
j
3
+ j
2
j
1
V ( j
1
j
2
j
3
, m
1
m
2
m
3
)=(1)
j
1
j
2
m
3
1
.
2j
3
+1
j
1
m
1
j
2
m
2
j
3
m
3

V ( j
1
j
2
j
3
, m
1
m
2
m
3
)=
(1)
j
1
j
2
m
3
(1)
j
3
+ j
2
j
1
1
.
2j
3
+1
j
1
m
1
j
2
m
2
j
3
m
3

V ( j
1
j
2
j
3
, m
1
m
2
m
3
)=(1)
j
3
m
3
2j
1
+2j
2
1
.
2j
3
+1
j
1
m
1
j
2
m
2
j
3
m
3

V ( j
1
j
2
j
3
, m
1
m
2
m
3
)=(1)
j
3
m
3
1
.
2j
3
+1
j
1
m
1
j
2
m
2
j
3
m
3

This 3j symbol is equal to Schwinger's X coefficient

X ( j
1
j
2
j
3
, m
1
m
2
m
3
)
. The advantage of
this symmetrised coefficients is that the introduction of the (see pag123 [73] )statistical weight factor
.
2j
3
+1
1/ 2
, removes an asymmetry between
j
3
and
j
1
, j
2
Chapter 11 The formula of Lagrange and Sylvester for function F of
matrix

M
134
11.1 Sylvester formula for Rabi oscillations full deduction
How
I will try to deduce by to methods one of them is to deduce the Lagrange interpolation from solwing the
system of equations taking into account Vandermonde determinant use the general Cramers rule and
inverse matrices the second one is I will deduce the Lagrange formula from [14] pag 287 and [61] pag
333
Eigenvalue problem and polynomial (Bezout)
Properties of determinants
Cramer's Rules
Inverse matrix
Vandermonde determinant and system of equation
Vandermonde determinant and Cramer's rule result Lagrange's interpolation formula:
11.2 Eigenvalues and Eigenvectors
Consider the special form of the linear system in which the right-hand side vector y is a multiple of the
solution vector x:
A x= x (11.2.1)
or, written in full,
a
11
x
1
+a
12
x
2
+...+a
1n
x
n
=\ x
1
a
21
x
1
+a
22
x
2
+...+a
2n
x
n
=\ x
2
... ... ... ... ...
a
n1
x
1
+a
n2
x
2
+...+a
nn
x
n
=\ x
n
(11.2.2)
This is called the standard (or classical) algebraic eigenproblem. System (11.2.1) can be rearranged into
the homogeneous form
( A\I) x=0 (11.2.3)
A nontrivial solution of this equation is possible if and only if the coefficient matrix A I is
singular. Such a condition can be expressed as the vanishing of the determinant
A\I=

a
11
\ a
12
... a
1n
a
21
a
22
\ ... a
2n

a
n1
a
n2
... a
nn
\

(11.2.4)
When this determinant is expanded, we obtain an algebric polynomial equation in \ of degree n:
135
P(\)=\
n
+o
1
\
n1
+...+o
n
=0 (11.2.5)
This is known as the characteristic equation of the matrix A. The left-hand side is called the
characteristic polynomial. We known that a polynomial of degree n has n (generally complex) roots 1,
2, . . ., n. These n numbers are called the eigenvalues, eigenroots or characteristic values of matrix A.
With each eigenvalue i there is an associated vector xi that satisfies
A x
i
=
i
x
i
This
x
i
is called an eigenvector or characteristic vector. An eigenvector is unique only up to a scale
factor since if x
i
is an eigenvector, so is x
i
where is an arbitrary nonzero number.
Eigenvectors are often normalized so that their Euclidean length is 1, or their largest component is
unity.
http://en.wikipedia.org/wiki/Equation_solving
Polynomial equations of degree up to four can be solved exactly using algebraic methods, of which the
quadratic formula is the simplest example. Polynomial equations with a degree of five or higher require
in general numerical methods (see below) or special functions such as Bring radicals, although some
specific cases may be solvable algebraically, for example
although some specific cases may be solvable algebraically, for example
4x
5
x
3
3 = 0
(by using the Rational root theorem)
In algebra, the rational root theorem (or rational root test) states a constraint on rational solutions (or
roots) of the polynomial equation
a
n
x
n
+a
n1
x
n1
+...+a
0
=0
with integer coefficients.
If a
0
and a
n
are nonzero, then each rational solution x, when written as a fraction
x=p/ q
in lowest
terms (i.e., the greatest common divisor of p and q is 1), satisfies
p is an integer factor of the constant term a
0
, and
q is an integer factor of the leading coefficient a
n
.
Thus, a list of possible rational roots of the equation can be derived using the formula
x=!
p
q
.
Example problem:
f ( x)=2x
3
+3x5
Possible Rational Roots:
!1,!5
!1,!2
=!1,!5,!
1
2
,!
5
2
Factored polynomial has only one real root:
f ( x)=( x1) (2x
2
+2x+5)
11.3 Properties of determinants
Properties of determinants see pag 340 [33]and for proof see pag 70 [14] so:
136
We shall list the basic properties of determinants .
1. The value of a determinant does not change if corresponding rows and columns are interchanged:

a
11
a
12
... a
1n
a
21
a
22
... a
2n
... ... ... ...
a
n1
a
n2
... a
nn

a
11
a
21
... a
n1
a
12
a
22
... a
n2
... ... ... ...
a
1n
a
2n
... a
nn

or more compactly
deta
ik
=deta
ki

Interchanging of the rows and columns is called transposition. A determinant in which such a change
has been made is said to be transposed. We can thus say that a transposed determinant equals the initial
one.
2. The sign of a determinant is changed if any two rows or any two columns are interchanged.
3. If two columns or rows are identical, the determinant is zero (this follows from the property 2).
4. A determinant is a linear form of the elements of a row or a column:
deta
ik
=

k =1
n
A
ik
a
ik
linear form of the elements of the i-th row
or
deta
ik
=

i=1
n
A
ik
a
ik
linear form of the elements of the k-th column
(the linear form of the variables x
1
, x
2
,... , x
n
is defined to be the linear homogenius function of these
variables i.e. the expression
f =a
1
x
1
+a
2
x
2
+...+a
n
x
n
)
5. If the elements of one row (or column) are multiplied by the algebraic cofactors of the elements of
another row (or column) and the products obtained are summated, the sum will be zero (this sum is a
determinant with two identical rows or columns; see the property 3).
6. If all the elements of a row (or column) contain a common factor, it can be written before the
determinant:

a
11
... a
1 k
... a
1n
... ... ... ... ...
oa
i 1
... oa
i k
... oa
i n
... ... ... ... ...
a
n1
... a
n k
... a
n n

=o

a
11
... a
1 k
... a
1 n
... ... ... ... ...
a
i 1
... a
i k
... a
i n
... ... ... ... ...
a
n1
... a
n k
... a
n n

(11.3.1)
7. If the elements of a row (or column) are the sum of two (or more) addends, the determinant equals
the sum of determinants in which the relevant addends are the elements of the given row (or column),
for example,
137

a
11
... a
1k
'
+a
1k
' '
... a
1n
a
21
... a
2k
'
+a
2k
' '
... a
2n
... ... ... ... ...
a
n1
... a
nk
'
+a
nk
' '
... a
nn

a
11
... a
1k
'
... a
1n
a
21
... a
2k
'
... a
2n
... ... ... ... ...
a
n1
... a
nk
'
... a
nn

a
11
... a
1k
' '
... a
1n
a
21
... a
2k
' '
... a
2n
... ... ... ... ...
a
n1
... a
nk
' '
... a
nn

8. The value of a determinant is not changed if to the elements of any row (or column) we add the
corresponding elements of another row (or column) after first multiplying them by the same constant
quantity. This property follows from properties 7, 6, and 3.
9. The product of two determinants of the same order,
deta
ik

and
detb
ik

, is a determinant
of the same order, detc
ik
, whose elements are expressed by the formulas
c
ik
=

m
a
i m
b
mk
11.4 The Method of Cofactors
See
http://tutorial.math.lamar.edu/Classes/LinAlg/MethodOfCofactors.aspx#Det_Cofactor_Defn3
So, before we actually give the method of cofactors we need to get a couple of definitions taken
care of.
det ( A)=A=

a
11
a
12
a
21
a
22

Definition 1
If A is a square matrix then the minor of
a
ij
, denoted by
M
ij
, is the determinant
of the submatrix that results from removing the i-th row and j-th column of A.
Definition 2
If A is a square matrix then the cofactor of a
ij
, denoted by C
ij
, is the number
(1)
i +j
M
ij
(11.4.1)
Theorem 1
If A is a nn matrix.
a) Choose any row say row I then,
det ( A)=a
i1
C
i1
+a
i2
C
i2
+...+a
i n
C
i n
(11.4.2)
138
b) Choose any column say column j, then,
det ( A)=a
1j
C
1j
+a
2j
C
2j
+...+a
n j
C
n j
(11.4.3)
Exemple:
A=
|
0 1 2
2 3 1
4 0 1

we have
A
11
=

3 1
0 1

=3 , A
12
=

2 1
4 1

=2 A
13
=

2 3
4 0

=12
We find the determinant by expansion of first row:
det ( A)=a
11
A
11
+a
12
A
12
+a
13
A
13
=03+1(2)+2(12)=26
11.5 Cramer's rule proof
Theorem :
Supose that A is an nn matrix. Then the solution to the system Ax=b is given by,
x
1
=
det ( A
1
)
det ( A)
, x
2
=
det ( A
2
)
det ( A)
, x
n
=
det ( A
n
)
det ( A)
(11.5.1)
Where A
i
is the matrix found by replacing the i
th
column of A with b
Proof:
The proof to this is actually pretty simple. First, because we know that A is invertible then we know
that the inverse exists and that det ( A)0 . We also know that the solution to the system can be
given by,
x=A
1
b (11.5.2)
From the section on cofactors we know how to define the inverse in terms of the adjoint of A. Using
this gives us,
x=
1
det ( A)
adj ( A) b=
1
det ( A)

C
11
C
21
... C
n1
C
12
C
22
... C
n2

C
1n
C
2n
... C
nn

(11.5.3)
Recall that C
ij
is the cofactor of a
ij
. Also note that the subscripts on the cofactors above appear
to be backwards but they are correctly placed. Recall that we get the adjoint by first forming a matrix
with
C
ij
in the ith row and jth column and then taking the transpose to get the adjoint.
Now multiply out the matrix to get:
139
x=
1
det ( A)

b
1
C
11
+b
2
C
21
+... b
n
C
n1
b
1
C
12
+b
2
C
22
+... b
n
C
n2

b
1
C
1n
+b
2
C
2n
+... b
n
C
nn

the entry of ith row of x which is x

i
in the solution, is
x
i
=
b
1
C
1i
+b
2
C
2i
+...+b
n
C
ni
det ( A)
Next let's define
A
i
=

a
11
a
12
... a
1i 1
b
1
a
1i+1
... a
1n
a
21
a
22
... a
2i 1
b
2
a
2i +1
... a
2n

a
n1
a
n2
... a
ni 1
b
n
a
ni +1
... a
nn

So, A
i
is the matrix we get by replacing the ith column of A with b . Now, if we were to compute
the determinate of A
i
by expanding along the ith column the products would be one of the b
i
s
times the appropriate cofactor. Notice however that since the only difference between A
i
and A is
the ith column and so the cofactors we get by expanding A
i
along the ith column will be exactly the
same as the cofactors we would get by expanding A along the ith column.
Therefore the determinant of A
i
is given be:
det ( A
i
)=b
1
C
1i
+b
2
C
2i
+b
n
C
ni
(11.5.4)
where C
k i
is the cofactor of
a
k i
from the matrix A. Note however that this is exactly the
numerator of x
i
and so we have
x
i
=
det ( A
i
)
det ( A)
as we wanted to prove.
11.6 Vandermonde determinant
see from [14] pag 94
Determinant
V
n
=

1 1 ... 1
k
1
k
2
... k
n
k
1
2
k
2
2
... k
n
2

k
1
n1
k
2
n1
... k
n
n1

(11.6.1)
Is called Vandermonde determinant.
140

1 1 ... 1
k
1
k
2
... k
n
k
1
2
k
2
2
... k
n
2

k
1
n1
k
2
n1
... k
n
n1

l
1
l
2
l
3

l
n
where l
1
stands for line 1 and so on
In order to calculate the (11.6.1) we subtract from each line the precedent line multiplied by k
1
so we have
l
2
l
1
k
1
=k
1
k
1
, k
2
k
1
, k
3
k
1
, ... k
n
k
1
l
3
l
2
k
1
=k
1
2
k
1
2
, k
2
2
k
1
2
, k
3
2
k
1
2
, ... k
n
2
k
1
2
etc
we get
V
n
=

1 1 ... 1
0 k
2
k
1
... k
n
k
1
0 ( k
2
k
1
) k
2
... ( k
n
k
1
) k
n

0 ( k
2
k
1
) k
2
n2
... ( k
2
k
1
) k
n
n2

we use (11.4.3) for the first column we get

V
n
=

k
2
k
1
... k
n
k
1
( k
2
k
1
) k
2
... ( k
n
k
1
) k
n

( k
2
k
1
) k
2
n2
... ( k
2
k
1
) k
n
n2

and we take out the common factors before the determinant like in (11.3.1) we get:

V
n
=( k
2
k
1
)( k
3
k
1
)... ( k
n
k
1
)V
n1
(11.6.2)

where
V
n1
=

1 ... 1
k
2
... k
n
k
2
2
... k
n
2

k
2
n2
... k
n
n2

(11.6.3)
Where(11.6.3) is Vandermonde determinant of degree (n-1)
We apply the same procedure and we get V
n2
and so on and finaly we get:
V
n
=( k
2
k
1
)( k
3
k
1
)... ( k
n
k
1
) (k
3
k
2
) ...( k
n
k
2
) ... (k
n
k
n1
)
(11.6.4)
141
11.7 Vandermonde determinant and Cramer's rule result Lagrange's
interpolation formula
See Hans-Dieter Reuter
http://www.joinedpolynomials.org
Lagrange interpolation formula is determined as a special case of polunomial transposition.
A number of points is determined with unique locations
x
j
y
i
= f ( x
j
)
0j n (11.7.1)
Therefore an interpolation polynomial is determined by as many terms.
y= f ( x)=

0 j n
a
i
x
i
(11.7.2)
The determinant of a Vandermonde matrix is equals the product of all possible differences. The
determinant is non zero for all locations are unique.
det (G)=

1in

0 ji
( x
i
x
j
)
(11.7.3)
A base polynomial is determined by Cramer's rule. Thus a source matrix is a variant of the base matrix
for which one column is replaced by a source. The determinant of a source matrix is determined
accordingly
det (Q
m
)=

1i n

0 ji

( xx
j
) , if i =m
( x
i
x) , if j =m
( x
i
x
j
) , otherwise
(11.7.4)
A base polynomials is determined by Cramer's rule. A number of differences and signs cancel.
w
j
=
det (Q
j
)
det (G)
=

i j
0in
( x
i
x)

i j
0in
( x
i
x
j
)
(11.7.5)
Lagrange's interpolations formula is determined by polynomial transposition:
f ( x)=

0 j n
w
j
y
i
(11.7.6)
From other source I found:
142
Fit N+1 points with an Nth degree polynomial
f(x) = exact function exact function of which only discrete values are known and used to establish an
interpolating or approximating function g(x)
g(x)= approximating or interpolating function. This function will pass through all specified
interpolation points (also referred to as data points or nodes)
The interpolations points or nodes are given as:
x
0
f ( x
0
) f
0
x
1
f ( x
1
) f
1
x
2
f ( x
2
) f
2

x
N
f ( x
N
) f
N
there exists only Nth degree polynomial that passes trough a given set of N+1 points. It's form is
expressed a a power series:
g( x)=a
0
+a
1
x+a
2
x
2
+a
3
x
3
+...+a
N
x
N
(11.7.7)
g(x) must match f(x) at the selected points
g( x
0
)= f
0
a
0
+a
1
x
0
+a
2
x
0
2
+...+a
N
x
0
N
=f
0
g( x
1
)= f
1
a
0
+a
1
x
1
+a
2
x
1
2
+...+a
N
x
1
N
= f
1
...
g( x
N
)=f
N
a
0
+a
1
x
N
+a
2
x
N
2
+...+a
N
x
N
N
= f
N
Solve set of simultaneous equations taking into account (11.5.1) that is (11.7.5):
143
Illustration 20
|
1 x
0
x
0
2
... x
0
N
1 x
1
x
1
2
... x
1
N
... ... ... ... ...
1 x
N
x
N
2
... x
N
N
|
a
0
a
1
...
a
N

=
|
f
0
f
1
...
f
N

(11.7.8)
So we obtain the (11.7.6)
Or explicitly from [14] pag 287 and [61] pag 333
we have
P( x)=

k =0
n
y
k
( xx
0
)( xx
1
)...( xx
k1
)...( xx
n
)
( x
k
x
0
)( x
k
x
1
)...( x
k
x
k1
) ...( x
k
x
n
)
(11.7.9)
(11.7.9)This is called the interpolating polynomial of Lagrange .
Which degree should the polynomial p(x) have? Good question. A line (i.e. a polynomial of degree 1)
can be drawn through two points (n 2) but not, in general, through three points. A parabola can be
drawn through three points but not through four. So the degree of p(x) should be at least n 1.
For n=3 from (11.7.9) we get:
p( x)=y
1
( xx
2
)( xx
3
)
( x
1
x
2
)( x
1
x
3
)
+y
2
( xx
1
)( xx
3
)
( x
2
x
1
)( x
2
x
3
)
+y
3
( xx
1
)( xx
2
)
( x
3
x
1
)( x
3
x
2
)
(11.7.10)
that the polynomial given by Eq. (11.7.10) indeed satisfies
p( x
1
)=y
1
, p ( x
2
)=y
2
, p( x
3
)=y
3
(11.7.11)
. Also, it is evident that you can write such a polynomial for any number of data points as long as all
the x
i
are different, so that the denominators in Eq. (11.7.10) are all nonzero.
So we will prove (11.7.5),(11.7.6),(11.7.9)and(11.7.10) by solving (11.7.8)
we will find the polynomial by Cramer's rule
p( x)=ax
2
+bx+c (11.7.12)
|
1 x
1
x
1
2
1 x
2
x
2
2
1 x
3
x
3
2
|
a
b
c

=
|
y
1
y
2
y
3

(11.7.13)
Using (11.5.1) we have
a=
|
1 x
1
y
1
1 x
2
y
2
1 x
3
y
3

det V
( 3)
( x
1
, x
2
, x
3
)
b=
|
1 y
1
x
1
2
1 y
2
x
2
2
1 y
3
x
3
2
det V
(3)
( x
1
, x
2
, x
3
)
c=
|
y
1
x
1
x
1
2
y
2
x
2
x
2
2
y
3
x
3
x
3
2
det V
(3)
( x
1
, x
2
, x
3
)
We examine Eq. (11.7.10) and find that p(x) can be viewed as a polynomial of degree 1 in the
variables y
i
and of degree 2 in x . It is also clear from Eq. (3) that the leading coefficient a of the
polynomial p(x) has the form of a polynomial of first order in x
i
divided by
144
( x
2
x
1
)( x
3
x
1
)( x
3
x
2
) . The only possible denominator in a is the Vandermonde determinant .
Let us have a rigorous proof. We can write the coefficient a using Eq. (11.7.10) As
a=y
1
(1)
1+3
( x
3
x
2
)
( x
2
x
1
)( x
3
x
1
)( x
3
x
2
)
+y
2
(1)
2+3
( x
3
x
1
)
( x
2
x
1
) ( x
3
x
1
)( x
3
x
2
)
+y
3
(1)
3+3
( x
2
x
1
)
( x
2
x
1
)( x
3
x
1
) ( x
3
x
2
)
=
a=y
1
1
( x
2
x
1
)( x
3
x
1
)
+y
2
1
( x
2
x
1
)( x
3
x
2
)
+y
3
1
( x
3
x
1
)( x
3
x
2
)
here is important to observe that we find the determinant by using (11.5.4) by finding the cofactors of
last column which are the Vandermonde determinants of 2 order.
In principle we can stop here and we can represent (11.7.12) as
p( x)=a( xp
i
) ( xq
j
) i , j=1,2,3
(11.7.14)
and for (11.7.11) we have
p( x
1
)=y
1
( x
1
p
2
)( x
1
p
3
)
( x
1
x
2
)( x
1
x
3
)
+y
2
( x
1
p
1
)( x
1
p
3
)
( x
2
x
1
)( x
2
x
3
)
+y
3
( x
1
p
1
)( x
1
p
2
)
( x
3
x
1
)( x
3
x
2
)
p( x
1
)=y
1
( x
1
p
2
)( x
1
p
3
)
( x
1
x
2
)( x
1
x
3
)
+y
2
0+y
3
0
p( x
1
)=y
1
1+y
2
0+y
3
0
p
2
=x
2
, p
3
=x
3
and the same procedure for p( x
2
) and p( x
3
) this is actually the Lagrange
idea by using (11.7.14) that lead clearly to Eq. (11.7.10).
In the case that you don't believe that any polynomial can be factorised in form of (11.7.14) we solve
the system (11.7.13) and find b and c coefficients but in these cases we dont have the Vandermonde
determinants for cofactors !
But for n= 3 is simple:

b=y
1
( x
3
2
x
2
2
)
( x
2
x
1
)( x
3
x
1
)( x
3
x
2
)
+y
2
( x
3
2
x
1
2
)
( x
2
x
1
) ( x
3
x
1
)( x
3
x
2
)
+y
3
( x
2
2
x
1
2
)
( x
2
x
1
)( x
3
x
1
) ( x
3
x
2
)
=
=y
1
( x
3
+x
2
)
( x
2
x
1
)( x
3
x
1
)
+y
2
( x
3
+x
1
)
( x
2
x
1
)( x
3
x
2
)
+y
3
( x
2
+x
1
)
( x
3
x
1
)( x
3
x
2
)
and for c we have
x
2
x
3
2
x
3
x
2
2
=x
2
x
3
( x
3
x
2
)
c=y
1
x
2
x
3
( x
3
x
2
)
( x
2
x
1
)( x
3
x
1
)( x
3
x
2
)
+y
2
x
3
x
1
( x
3
x
1
)
( x
2
x
1
)( x
3
x
1
)( x
3
x
2
)
+y
3
x
2
x
1
( x
2
x
1
)
( x
2
x
1
)( x
3
x
1
)( x
3
x
2
)
=
=y
1
x
2
x
3
( x
2
x
1
)( x
3
x
1
)
+y
2
x
3
x
1
( x
2
x
1
)( x
3
x
2
)
+y
3
x
2
x
1
( x
3
x
1
)( x
3
x
2
)
so we now put a, b, and c in (11.7.12) for the same coefficients of y
1
so we have
145
ax
2
+bx+c=x
2
x( x
3
+x
2
)+x
2
x
3
=( xx
2
)( xx
3
)
the same for y
2
and y
3
so finally we get
p( x)=ax
2
+bx+c
=y
1
( xx
2
)( xx
3
)
( x
1
x
2
)( x
1
x
3
)
+y
2
( xx
1
)( xx
3
)
( x
2
x
1
)( x
2
x
3
)
+y
3
( xx
1
)( xx
2
)
( x
3
x
1
)( x
3
x
2
)
which was to be proved.
11.8 Cayley-Hamilton Theorem
http://www.efgh.com/math/cayleyhamilton.htm
11.8.1 The Theorem
Some mathematical theorems are especially beautiful. It's hard to say what makes a theorem beautiful,
but two properties come to mind:
1. It's simple to state.
2. It's hard to prove.
In my opinion, one very beautiful theorem is the Cayley-Hamilton Theorem of matrix algebra. It
states that if p(z) is the characteristic polynomial of an n x n complex matrix A, then p(A) is the zero
matrix, where addition and multiplication in its evaluation are the usual matrix operations, and the
constant term p
0
of p(z) is replaced by the matrix p
0
I.
Recall that the characteristic polynomial of A is given by
p(z) = det(A-zI).
11.8.2 The Simple But Invalid Proof
At this point, students sometimes naively substitute A for z in the definition of the characteristic
polynomial and falsely conclude that the Cayley-Hamilton Theorem is trivial:
Why isn't p(A) = det(A-AI) = det(A-A) = det(O) = 0?
There are two obvious fallacies. First of all, zI in the definition of the characteristic polynomial
represents the multiplication of a matrix by a scalar, but AI is the multiplication of two matrices.
Moreover, the argument given above seems to prove that a matrix is equal to a scalar.
Actually, this argument is valid in the special case where A is a 1 x 1 matrix, and there is essentially no
difference between matrix and scalar operations; but in that case the Cayley-Hamilton Theorem really
is trivial.
11.8.3 An Analytic Proof
There are many proofs of the Cayley-Hamilton Theorem. I must admit that I have trouble following
most of them, because they involve rather advanced algebra or combinatorics. A more analytic
argument, like the one presented here, is more suited to my own training and talents.
It helps to work out the general 2 x 2 case:
146
| a b |
A = | |
| c d |
The characteristic polynomial of A is
| a-z b |
p(z) = | | = (a-z)(d-z) - bc = z
2
- (a+d)z + ad - bc.
| c d-z |
Substituting A for z gives:
p(A) = A
2
- (a+d)*A + (ad-bc)*I =
| a b | | a b | | a b | | 1 0 |
| | * | | - (a+d) * | | + (ad-bc) * | | =
| c d | | c d | | c d | | 0 1 |
| a
2
+bc ab+bd | | a
2
+ad ab+bd | | ad-bc 0 |
| | - | | + | | =
| ac+cd bc+d
2
| | ac+cd ad+d
2
| | 0 ad-bc |
| a
2
+bc-a
2
-ad+ad-bc ab+bd-ab-bd | | 0 0 |
| | = | |.
| ac+cd-ac-cd bc+d
2
-ad-d
2
+ad-bc | | 0 0 |
To prove the theorem in the general case, let u be an eigenvalue of A, and let x be the corresponding
eigenvector (expressed as a column vector). Then
Ax = ux.
Using elementary properties of scalar and matrix operations gives
A
2
x = (AA)x = A(Ax) = A(ux) = u(Ax) = u(ux) = u
2
x.
It can be shown in general that
[1] A
k
x = u
k
x, for k = 0, 1, 2, ... n,
where A
0
= I.
Let the characteristic polynomial of A be
p(z) = p
n
z
n
+ p
n-1
z
n-1
+ p
n-2
z
n-2
+ ... + p
0
.
Then multiply each equation in [1] above by p
k
and add them to obtain
p(A)x = p(u)x.
Now p(u) is zero because u is an eigenvalue of A. Hence p(A)x = 0 for every eigenvector x of A.
If A has n linearly independent eigenvectors, this implies that p(A) must be the zero matrix.
147
If A does not have n linearly independent eigenvectors, we construct a sequence A
1
, A
2
, ... of matrices
whose limit is A, each of which has n linearly independent eigenvectors. Then if p
j
(z) is the
characteristic polynomial of A
j
, p
j
(A
j
) = O. Since all coefficients in p
j
(A
j
) are continuous functions of
the matrix entries, the same is true of the limit p(A).
To create such a sequence, it is sufficient to construct matrices arbitrarily close to A, each of which has
n linearly independent eigenvectors.
First, we need a simple lemma. The matrix A, like all complex matrices, is similar to an upper
triangular matrix, i.e., there is a nonsingular matrix Q for which
Q
-1
AQ
is upper triangular. This result is well-known, but a simple proof is given in Appendix A.
The eigenvalues of an upper triangular matrix appear along its principal diagonal. There is an upper
triangular matrix T arbitrarily close to Q
-1
AQ with n distinct eigenvalues. Then QTQ
-1
is arbitrarily
close to A and has the same n distinct eigenvalues as T.
A matrix with n distinct eigenvalues has n distinct eigenvectors. If these eigenvectors were linearly
dependent, they would span a space of dimension less than n. The mapping defined by the matrix,
restricted to this space, would still have the same n distinct eigenvalues, which is impossible. Hence the
eigenvectors are linearly independent.
11.8.4 Proof for Commutative Rings
This proves the Cayley-Hamilton Theorem for complex matrices, but it is also true for matrices over
more general commutative rings.
The proof of this is actually fairly simple. Our experience in proving the 2 x 2 case shows the way. The
expression for each entry in p(A) is a polynomial in n
2
variables, which are the entries of A. It's not just
any polynomial, but one which takes on the value zero for all values of the variables. That can happen
only if all the coefficients are zero when like terms are combined. (This seems to be an obvious result,
but it requires proof, so one is given in Appendix B.) Hence the polynominal evaluates to zero in any
other algebraic entity that has all the necessary operations.
It might appear that the ring must have a unit. However, if we refrain from combining like terms, we
will have a sum of monomials, each prepended by a + sign or a - sign. Even in the complex field,
cancellation is possible only if every positive monomial has a corresponding negative monomial. They
will cancel in a ring, too, even if the ring has no unit.
11.8.5 Appendix A. Every Complex Matrix is Similar to an Upper Triangular Matrix.
Let A be an n x n complex matrix. We show, by induction on n, that it is similar to an upper triangular
matrix.
For n = 1 the assertion is trivial because A is already upper triangular.
In other cases, let u be an eigenvalue of A and let x
1
be a corresponding eigenvector. Extend this to a
set x
1
, x
2
, ..., x
n
of linearly independent vectors, and let Q be the matrix whose columns are x
1
, x
2
, ...,
148
x
n
.
Then if e
1
is the column vector with 1 in its first row and zeros elsewhere, Me
1
is the first column of M
for any n x n matrix M. Hence
Q
-1
AQe
1
= Q
-1
Ax
1
= Q
-1
ux
1
= uQ
-1
x
1
= ue
1
,
and the first column of Q
-1
AQ is ue
1
. Hence it can be partitioned as follows:
| u v |
| |
| 0 B |,
where v is an (n-1)-element row vector, B is an (n-1) x (n-1) matrix, and 0 is all zeros. By inductive
hypothesis, R
-1
BR is upper triangular for some nonsingular matrix R, so the following matrix is the
required upper triangular matrix similar to A:
| 1 0 | | 1 0 |
| | * Q
-1
AQ * | |
| 0 R
-1
| | 0 R |
11.8.6 APPENDIX B. A Complex Polynomial Is Identically Zero Only If All Coefficients
Are Zero
If a polynomial is identically zero, all of its coefficients are zero, when like terms are combined, of
course.
The proof is by induction on the number of independent variables.
For a polynomial p(z) in one variable, we simply note that p
(k)
(0) is the k! times the coefficient of z
k
. If
the polynomial is identically zero, all of its derivatives are also identically zero, and all of its
coefficients must be zero.
A polynominal in n variables can be rearranged so it is a polynomial in one variable, and each of its
coefficients is a polynomial in the remaining n-1 variables.
By the result for one variable, every such coefficient is zero for all values of its independent variables.
Hence by inductive hypothesis all of its coefficients are zero.
Although the coefficients of an identically zero complex polynomial are all zero, this is not true over
finite fields. If N is the number of elements in a finite field, then z
N
- z = 0 for every element z of the
field. (The proof given above breaks down in this case. Although formal derivatives can be defined, N!
is zero, as it appears in the formal derivative.)
11.8.7 From Wikipedia, the free encyclopedia
http://en.wikipedia.org/wiki/Cayley-Hamilton_theorem
As a concrete example, let
A=
(
1 2
3 4
)
149
Its characteristic polynomial is given by
p(\)=det (\ I
2
A)=det
(
\1 2
3 \4
)
=
(\1)(\4)(2)(3)=\
2
5\2
The CayleyHamilton theorem claims that, if we define
p(X) = X
2
5X 2I
2
,
then
p( A)=A
2
5A2I
2
=
(
0 0
0 0
)
which one can verify easily.
A bogus "proof": p(A) = det(AI
n
A) = det(AA) = 0
One elementary but incorrect argument for the theorem is to "simply" take the definition
p(\)=det (\ I
n
A)
and substitute A for , obtaining
p( A)=det ( A I
n
A)=det ( AA)=0
There are many ways to see why this argument is wrong. First, in CayleyHamilton theorem, p(A) is an
nn matrix. However, the right hand side of the above equation is the value of a determinant, which is
a scalar. So they cannot be equated unless n=1 (i.e. A is just a scalar). Second, in the expression det(I
n
A), the variable actually occurs at the diagonal entries of the matrix I
n
A. To illustrate, consider
the characteristic polynomial in the previous example again:
det
(
\1 2
3 \4
)
If one substitutes the entire matrix A for in those positions, one obtains
det
(
(
1 2
3 4
)
1 2
3
(
1 2
3 4
)
4)
in which the "matrix" expression is simply not a valid one. Note, however, that if scalar multiples of
identity matrices instead of scalars are subtracted in the above, i.e. if the substitution is performed as
150
det
(
(
1 2
3 4
)
I
2
2I
2
3I
2
(
1 2
3 4
)
4I
2
)
then the determinant is indeed zero, but the expanded matrix in question does not evaluate to AI
n
A;
nor can its determinant (a scalar) be compared to p(A) (a matrix). So the argument that p(A) = det(AI
n

A) = 0 still does not apply.
11.9 SYLVESTER'S MATRIX THEOREM
http://sepwww.stanford.edu/sep/prof/fgdp/c5/paper_html/node3.html#SECTION001200000000000000
00
Sylvester's theorem provides a rapid way to calculate functions of a matrix. Some simple functions of a
matrix of frequent occurrence are A
1
and A
N
(for N large). Two more matrix functions which
are very important in wave propagation are e
A
and e
1/ 2
.Before going into the somewhat abstract
proof of Sylvester's theorem, we will take up a numerical example. Consider the matrix
A=
|
3 2
1 0


It will be necessary to have the column eigenvectors and the eigenvalues of this matrix; they are given
by

|
3 2
1 0
|
1
1

=1
|
1
1

|
3 2
1 0
|
2
1

=2
|
2
1

Since the matrix A is not symmetric, it has row eigenvectors which differ from the column vectors.
These are
|1 2
|
3 2
1 0

=1|1 2
| 1 1
|
3 2
1 0

=2|1 1
We may abbreviate above equations by
Ac
1
=\
1
c
1
Ac
2
=\
2
c
2
r
1
A=\
1
r
1
r
2
A=\
2
r
2
(11.9.1)
The reader will observe that r or c could be multiplied by an arbitrary scale factor and (11.9.1) would
still be valid. The eigenvectors are said to be normalized if scale factors have been chosen so that
r
1
c
1
=1
and
r
2
c
2
=1
.It will be observed that
r
1
c
2
=0
and
r
2
c
1
=0
,a general result to be
151
established in the exercises.
Let us consider the behavior of the matrix
c
1
r
1
.
c
1
r
1
=
|
1
1

|1 2=
|
1 2
1 2

Any power of this matrix is the matrix itself, for example its square.
|
1 2
1 2
|
1 2
1 2

=
|
1 2
1 2

This property is called idempotence (Latin for self-power). It arises because

(c
1
r
1
)(c
1
r
1
)=c
1
(r
1
c
1
) r
1
=c
1
r
1
.The same thing is of course true of . Now notice that the matrix
c
1
r
1
is ``perpendicular'' to the matrix
c
2
r
2
, that is
|
2 2
1 1
|
1 2
1 2

=
|
0 0
0 0

since
r
2
and
c
2
are perpendicular.
Sylvester's theorem says that any function f of the matrix A may be written
f ( A)= f (\
1
)c
1
r
1
+f (\
2
)c
2
r
2
The simplest example is f ( A)=A
A=\
1
c
1
r
1
+\
2
c
2
r
2
=
1
|
1 2
1 2

+2
|
2 2
1 1

=
|
3 2
1 0

(11.9.2)
Another example is
A
2
=1
2
|
1 2
1 2

+2
2
|
2 2
1 1

=
|
7 6
3 2

The inverse is
A
1
=1
1
|
1 2
1 2

+2
1
|
2 2
1 1

=
1
2
|
0 2
1 3

The identity matrix may be expanded in terms of the eigenvectors of the matrix A.
A
0
=I =1
0
|
1 2
1 2

+2
0
|
2 2
1 1

=
|
1 0
0 1

Before illustrating some more complicated functions let us see what it takes to prove Sylvester's
theorem. We will need one basic result which is in all the books on matrix theory, namely, that most
matrices (see exercises) can be diagonalized. In terms of our 22 example this takes the form
|
r
1
r
2

A| c
1
c
2
=
|
\
1
0
0 \
2

(11.9.3)
Where
|
r
1
r
2

| c
1
c
2
=
|
1 0
0 1

(11.9.4)
Since a matrix commutes with its inverse, (11.9.4)implies
152
| c
1
c
2

|
r
1
r
2

=
|
1 0
0 1

(11.9.5)
Postmultiply (11.9.3) by the row matrix and premultiply by the column matrix. Using(11.9.5), we get

A=| c
1
c
2

|
\
1
0
0 \
2
|
r
1
r
2

(11.9.6)
Equation (11.9.6) is(11.9.2) in disguise, as we can see by writing(11.7.9) as
A=| c
1
c
2

|
\
1
0
0 0

+
|
0 0
0 \
2
|
r
1
r
2

=
| c
1
c
2

|
\
1
0
0 0
|
r
1
r
2

+| c
1
c
2

|
0 0
0 \
2
|
r
1
r
2

=
\
1
c
1
r
1
+\
2
c
2
r
2
Show the Cayley-Hamilton theorem, that is, if
0=f (\)=det ( A\ I )=p
0
+p
1
\+p
2
\
2
+... p
n
\
n
(11.9.7)
then
f ( A)=p
0
+p
1
A+p
2
A
2
+... p
n
A
n
=0 (11.9.8)
O=

0 0 ... 0
0 0 ... 0
... ... ... ...
0 0 ... 0

Verify that, for a general 22 matrix A, for which

\
1
\
2
c
1
r
1
=
(\ IA)
(\
2
\
1
)
where
\
1
and
\
2
are eigenvalues of A. What is the general form for
c
2
r
2
?
11.10 Final formula
Now using (11.9.7)and(11.9.8)that was proved in paragraph 11.8.3 and the sentence from and [61] pag
332 where is written that we can replace in Lagrange interpolation P(x) with P( A) or P( M) that
is a function of matrix so (11.7.9) become (see also [62] ):
153
F (

M)=

k =1
N

i =1,i k
N
(

M\
i

I )

i=1, ik
N
(\
k
\
i
)
F(\
k
) (11.10.1)
Exemple 1

M is 2D matrix
F (

M)=
(

M\
1

I )
(\
2
\
1
)
F (\
2
)+
(

M\
2

I )
(\
1
\
2
)
F(\
1
) (11.10.2)
Exemple 2

M is 3D matrix
F (

M)=
(

M\
2

I )(

M\
3

I )
(\
1
\
2
)(\
1
\
3
)
F (\
1
)+
+
(

M\
3

I )(

M\
1

I )
(\
2
\
3
)(\
2
\
1
)
F (\
2
)+
(

M\
1

I )(

M\
2

I )
(\
3
\
1
)(\
3
\
2
)
F(\
3
)
(11.10.3)
Exemple 3 by collecting the coefficients at the same power we have for (11.10.2):
F (

M)=
\
1
F(\
2
)\
2
F (\
1
)
(\
1
\
2
)

I +
F (\
1
)F(\
2
)
(\
1
\
2
)

M (11.10.4)
We can do it and for (11.10.3) and collect the coefficients at the same power an to get a general
formulation which is deduced in [62] .
Chapter 12 Time evolution two level atom Rabi frequency
Objectives:
Two level atom
Time evolution
The Pictures
Solution I
Solution II Kuno = skully
Bloch equations
154
Density matrix
12.1 Two level atom
A simple model depicting two level atom is:
Here we assumed, without loss of generality, that the
state 1 has the energy

1
2
o
0
, while the
excited state 2 has the energy
1
2
o
0
. Or we
can assume that 1 has the zero energy , and the
energy for the exited state 2 is then
o
0
.
the problem is where we must to
see pag 151 [65] we have
H
0
a= o
a
a
H
0
b= o
b
b

(12.1.1)
155
Fig 22 Atomic energy level diagram where the E=0 level is taken
halfway between the two levels see pag 92 [29] .
g
e
o
0
2
1
1
2
o
0
=E
e

1
2
o
0
=E
g
E=0
Fig 21
Laser field
o
0
o
L
A
1
2