Escolar Documentos
Profissional Documentos
Cultura Documentos
Research Statement: 1 Summary and Goals
Enviado por
Marcos DuarteDescrição original:
Título original
Direitos autorais
Formatos disponíveis
Compartilhar este documento
Compartilhar ou incorporar documento
Você considera este documento útil?
Este conteúdo é inapropriado?
Denunciar este documentoDireitos autorais:
Formatos disponíveis
Research Statement: 1 Summary and Goals
Enviado por
Marcos DuarteDireitos autorais:
Formatos disponíveis
Research Statement
Anton Khoroshkin
Summary and Goals
In my research I develop and apply new homological methods and theories to various questions of mathematical physics, representation theory, and algebraic topology. Section 2 below contains the description of my (joint) results that have already been published. Section 3 is devoted to the future directions and projects. Among the most important future projects/problems I should mention the following: Describe a natural homological theory of BV-algebras with coecients in a right module applicable to the perturbative Chern-Simons theory, topological quantum eld theory and realization of nonbased mapping spaces; Implement homological computations for operads over nite elds using the theory of Gr obner bases; Develop combinatorial and asymptotical methods in the theory of operads; Develop the theory of Gr obner bases for various operad-like algebraic structures such as dioperads, coloured operads, algebras over PBW operads, n-operads;
Research overview, important results
My research is primarily concentrated on homological computations and methods that might be applied in dierent areas of mathematics such as representation theory, algebraic topology and mathematical physics.
2.1
Lie algebra cohomology and Koszul property for algebras
Homological computations for innite dimensional Lie algebras was initiated in the 70s by means of what is nowadays known as the formal geometry [23]. Similar cohomology theory which turns out to be extremely useful in mathematical physics is known as BRST-cohomology. The Koszul property is an important homological tool for quadratic algebras discovered by Priddy [39] and was extensively used in dierent areas of algebra and geometry [38]. Using these two general methods mentioned in the title, I was able to make two particular computations in my PhD thesis [7]. Firstly, I was able to carry out a new computation of the syzygies of the Pl ucker embedding of the Grassmanian of two-dimensional planes which is much simpler than the one previously known. Secondly, I was able to compute the Lie algebra cohomology of the Lie algebra of formal vector elds on the plane with coecients in the symmetric powers of its coadjoint representation. The conjectural answer for the second question was well-known as one of the main conjectures of formal geometry due to B. L. Feigin, D. B. Fuchs and I. M. Gelfand ([21, 22, 13]). In order to do these computations, I developed several new general methods that might be applicable in many other situations. For example, in a joint work with A. Gorodentsev, A. Rudakov [6] which was motivated by our attempts to understand the crucial result of N. Berkovits on superstring theory [11, 12] we present a very general unied method of syzygy computations.
2.2
Operads and Koszul property
Later on I concentrated on the study of the notion of Koszul duality for various algebraic structures since it was known as a helpful method in dierent mathematical contexts, see [28]. The notion of an operad was rst invented by topologists. (Operads were known in pure algebra under the name of a variety of algebras and was introduced for the purposes of describing identities for various types of algebras, see [18].) Namely, if one takes an algebra of some type, i.e. a set with some operations on it, and removes the underlying set, what remains is the collection of all operations one can dene. This collection with the prescribed rules of compositions is what one calls an operad. The machinery provided by operads while studying various types of algebras became extremely useful in dierent areas of mathematics. For example, the rational homotopy theory due to Quillen and Sullivan [40] as well as Tamarkins approach to the deformation quantization [45, 33] were based on this machinery. My rst application of the operad theory was the proof of several conjectures by B. Feigin and An. Kirillov about the dimensions of the double Orlik-Solomon algebras (certain quadratic algebras which generalize the cohomology ring of a hyperplane arrangement of type An , see [31]). The nal results are published in joint with M. Berstein and V. Dotsenko articles [3, 1]. Namely, we found an operadic structure on the union of the double Orlik-Solomon algebras and shown the isomorphism of this operad with the operad of Bi-Hamiltonian algebras. While making manipulations with the Hilbert series of Sn -characters we found an interesting nontrivial example of an application of the Koszul duality for operads in the description of the symmetric group action on the spaces of n-ary operations. The method we use in [3] is quite general and may be applied in other similar situations.
2.3
Gr obner bases for operads
It is now well-known that applications of the operad theory in general (and, in particular, to verications of the Koszul property) are really dicult in particular computations. There was no known arithmetic of operations similar to the arithmetic of integers or polynomials (by an arithmetic we mean the usual notion of divisibility). The good analogue of multiplication for the operadic data is the composition of operations. But the action of the symmetric groups on the entries of operations do not allow to give a natural denition of divisibility. I found a solution to this problem using the notion of Shue operads introduced in a joint with V. Dotsenko paper [2]. The key idea was to forget about a certain part of the action of the symmetric group. In spite of being a very simple idea, it allowed us to introduce a theory of monomials, their divisibility and compatible orderings of monomials for operads. Summarizing these notions, we came up with the notion of Gr obner bases for operads (also presented in [2]). Gr obner bases is a remarkable technical tool initiated in the commutative algebra setting by Buchberger [14] which allows one to solve systems of equations with many unknowns (see [44] for a brief introduction). The theory of Gr obner bases for operads made it possible to provide a unied proof of the existing computational results in the eld as well as to prove some new results. It is clear that there are many topics that can be successfully approached by these new methods.
2.4
Resolutions and homology computations via Gr obner bases.
In particular, I want to mention some homological applications of the theory of Gr obner bases. With each given Gr obner basis of an operad we associate a free resolution of an operad which is much smaller than the standard one (joint work with V. Dotsenko [4]). This presents an eective method of homology computation of an operad. A general construction we gave is based on a analog of the inclusion-exclusion principle. Among other examples we found a direct homology computation for some non-quadratic operads. We were able to compute the homology of the so-called BV-operad [25] (also known as the homology of the framed little discs operad). The answer we obtained explains the mysterious connection between the BV operad
and the operad of compactied moduli spaces of stable curves of genus zero [26] (noticed by BarranikovKontsevich [9]). Though a very recent development, shue operads have been covered in a forthcoming textbook on algebraic operads by J.-L. Loday and B. Vallette [34]. In joint with V. Dotsenko [5] and B. Shapiro [8] papers we apply shue operads to the so-called pattern avoidance in permutations which is a very active area of algebraic combinatorics. (As we were informed by S. Kitaev, the material of [5, 8] will be included in his forthcoming textbook on this subject.)
3
3.1
Ongoing projects
BV algebras and mapping spaces
A structure of Batalin-Vilkovisky algebra [25] naturally appears in dierent subjects of algebraic topology and mathematical physics. For example, the homology of the space of nonbased loops Maps(S 1 , X ) admits a BV structure if X is a compact manifold (due to Chas-Sullivan string topology [16]). Another construction naturally appears in the perturbative Chern-Simons theory [15] and in BF theories [37]. BV-algebras are extensively used in TCFT [17], TQFT [42] and in Calabi-Yau categories [20]. We want to develop a natural homology theory of BV algebras such that the resulting invariants of the classes of BV-algebras will give new approaches to simplicial perturbative Chern-Simons theory, quantum cohomology and many other theories. Namely, since the operad f E2 of framed little discs is formal in dimension 2 ([43]) we may identify homotopy BV-algebras and f E2 -algebras. The union of conguration spaces f Conf (M ) of points (with frames) on a given surface M admits a natural structure of a topological right module over the framed little discs operad. Therefore one may consider the derived tensor product over the operad f E2 of the right module of chains on f Conf (M ) and any BV-algebra considered as a left f E2 -module. Let us mention two possible application of this denition. 3.1.1 Application to mapping spaces. The mentioned below application should be important for the purposes of algebraic topology. Mays recognition principle explains that any topological algebra over the operad of little discs Ed is homotopy equivalent to the space of based loops of dimension d. I.e. there is a natural action of Ed on Maps((S d , pt), (X, pt)). The orthogonal group SO(d 1) acts on (S d , pt) by rotations around the earth axis and therefore there is a natural structure of topological f Ed -algebra on the space Maps((S d , pt), (X, pt)). The described above tensor product of modules over an operad is well dened for any d-dimensional manifold M d and we come up with a nice approximation of the space of nonbased maps: Maps(M d , X ) is homotopy equivalent to f Conf (M d ) f Ed Maps((S d , pt), (X, pt)). 3.1.2 Application to the TQFT. f E1 -algebras coincide with E1 -algerbas that are just homotopy associative algebras. The derived tensor product of congurations on a circle and associative algebra A coincides with its Hochshcild homology HH q (A) = T orAAop (A, A). Therefore our homology theory (bered product over operad f Ed ) should be also considered as a natural generalization to higher dimension of the Hochschild homology: Let A be a f Ed algebra. The natural embedding of a (d 1)-dimensional disc into a d-dimensional disc via equator denes a morphism of operads: f Ed1 f Ed and therefore one has a f Ed1 -algebra structure on A. Let HS d1 (A) := f Conf (S d1 ) f Ed1 A be the corresponding bered product. The gluing of cylinders (S d1 [0, 1/2]) (S d1 [1/2, 1]) (S d1 [0, 1]) denes an algebra structure on HS d1 (A). Moreover there are left and right action of the algebra HS d1 (A) on A itself. The following isomorphism exists for every f Ed -algebra A:
d1 (A) HS d (A) := f Conf (S d )f Ed A (A, A) = T orHS q
If, in addition, the algebra A has an invariant scalar product one may identify T or and Ext in the above relation. Therefore the inner product on Ext-groups denes an algebra structure 3
on HS d (A). The action of the orthogonal group SO(d + 1) (via rotations of a sphere S d ) and multiplication (from Ext) generate a f Ed+1 -algebra structure on HS d (A) that may be generalized even to a (d + 1)-dimensional TQFT by the similar construction with conguration spaces. We are going to clarify this rough denition of a functor from f Ed -algebras with invariant pairing to (d + 1)-TQFTs. For d = 1 this coincides with a well known equivalence of categories of Frobenius algebras and (1 + 1)-TQFTs ([32]). Our computation of the homology of BV-operad made in [4] and methods discovered by the theory of Gr obner bases should provide us with direct denitions and computations of the prescribed homology. (This is a joint project with N. Markarian.)
3.2
Operads in positive characteristic and over a ring
The importance to understand the operad theory while working over a eld of positive characteristic can be illustrated by a well-known topological result formulated, for example, in Mandells paper [35]. The statement is (roughly) as follows. There is a unique (up to homotopy) action of the cobrant resolution (over Z) of an operad of commutative algebras on the space of singular cochains of a simply-connected topological space. Moreover, two (nilpotent, nite type) spaces are weakly homotopically equivalent if and only if their singular cochain complexes are quasi-isomorphic as modules over the corresponding operad (the so-called E -operad). Very little is known about operads over Z except for their denitions and general statements that can hardly be applied in concrete computations. For example, any realization of the E -operad is too big for any direct computations. The main problem is the modularity of representations of the symmetric groups over nite elds when the number of permuting elements is large compared to the characteristic of the base eld. On the other hand, the notion of shue operads and the corresponding theory of Gr obner bases are well dened even in this case. Therefore, if the coecients of the leading monomials of the corresponding Gr obner basis are invertible elements of the base ring then one can obtain the free resolutions as it was done in [4]. These resolutions will be free operads but will not be cobrant objects in the corresponding category. In spite of non-cobrance, the obtained free resolutions still contain a lot of information about the homotopy theory of algebras over the initial operad. For example, the natural homology theories and deformation complexes known for commutative algebras with divided powers and for restricted Lie algebras [29] may be covered by this approach. The paper of E.Hobeck [30] should be considered as a possible attempt in this direction.
3.3
Hilbert series of operads with nite Gr obner bases
The Hilbert series of an associative algebra with a nite Gr obner basis is a rational function [47]. This statement is extremely useful in the asymptotical and combinatorial approach to the theory of associative algebras [48]. A natural question about appropriate class of generating functions can be posed within the operad theory. In a joint project with D. Piontkovski, we plan to show that the Hilbert series of a non-symmetric operad with a nite Gr obner basis should be an algebraic function. On the other hand, exponential Hilbert series of symmetric operad with a nite shue Gr obner basis (under some mild assumptions) should be a solution of a dierential equation with algebraic coecients. Moreover we are going to present an eective algorithm of computing the Hilbert series for an operad with a given Gr obner basis as well as to give some bounds on the order of occurring dierential equation. As a corollary, this should allow us to present a list of possible Hilbert series of PBW operads with a small number of generators. The special case of shue operads with nite Gr obner (even monomial) bases is directly related to the theory of (consecutive) pattern avoidance. Homological theory for operads adopted to this special case was applied by the applicant jointly with B. Shapiro. For a given collection of patterns (with mild assumptions satised in a huge amount of cases) we nd a linear dierential equation with polynomial coecients such that the inverse function to the exponential gener-
ating function of the number of permutations avoiding all patterns from the given collection is a solution of this equation, see [8]. In a current joint with B. Shapiro project we plan to study several asymptotical problems in the theory of pattern avoidance where one might be able to achieve a substantial progress using our homological approach.
3.4
Gr obner bases for various algebraic structures.
Another area to be approached in this project is to develop a constructive arithmetic theory of operad-like structures. In particular, the adopted theory of Gr obner bases will be extremely useful for various associative structures built from labeled graphs. For example, the case of dioperads [24], which describes tree-type operations with several inputs and several outputs will be benecial for dierential geometry. The case of coloured operads [49], where the inputs and the outputs could be of several dierent types (colours), has applications to the operad theory itself and will be useful while obtaining formulas connecting the simplicial and dierential worlds (at present only the case of simplexes of dimension one is known to the specialists [36]). Higher category theory and the case of n-operads [10] should also be attacked by similar methods. Besides developing the general methods we are going to consider particular examples where the method of Gr obner bases should be useful. Several non-quadratic operads naturally appear in projective geometry and in quantum mechanics. Namely, Alternative algebras, Jordan algebras and special Jordan algebras [27, 46]. (This is a joint project with V.Dotsenko.)
References
Cited publications and preprints by A. Khoroshkin [1] M. Bershtein, V. Dotsenko, A. Khoroshkin. Quadratic algebras related to the bihamiltonian operad. IMRN 2007, no. 24, Art. ID rnm122, 30 pp. [2] V. Dotsenko, A. Khoroshkin. Gr obner bases for operads Duke Math. J. 153 (2010), no. 2, 363396. [3] V. Dotsenko, A. Khoroshkin. Character formulas for the operad of two compatible brackets and for the bi-Hamiltonian operad Funct. Anal. Appl. 41 (2007), no. 1, 117 [4] V. Dotsenko, A. Khoroshkin. math.arxiv:0912.4895, 24 pp. Free resolutions via Gr obner bases Preprint
[5] V. Dotsenko, A. Khoroshkin. Anick-type resolutions and consecutive pattern avoidance Preprint math.arXiv:1002.2761, 16 pp. [6] A. Gorodentsev, A. Khoroshkin, A. Rudakov. On syzygies of highest weight orbits. Moscow Seminar on Mathematical Physics. II, 79120, Amer. Math. Soc. Transl. Ser. 2, 221, Amer. Math. Soc., Providence, RI, 2007 [7] A. Khoroshkin. Formal geometry and algebraic invariants of geometric structures. PhD thesis Moscow State University, (russian), 2007. [8] A. Khoroshkin; B. Shapiro. Using homological duality in consecutive pattern avoidance. Preprint math.arXiv:1009.5308, 12 pp. Cited publications by other authors [9] S. Barannikov, M. Kontsevich. Frobenius manifolds and formality of Lie algebras of polyvector elds. Internat. Math. Res. Notices 1998, no. 4, 201215.
[10] M. Batanin. The Eckmann-Hilton argument and higher operads. Adv. Math. 217 (2008), no. 1, 334-385. [11] N. Berkovits. Super-Poincare Covariant Quantization of the Superstring. JHEP 0004 (2000) 018, see also arXiv:hep-th/0001035. [12] N. Berkovits. ICTP Lectures on Covariant Quantization of the Superstring. Preprint arXiv:hep-th/0209059. [13] J. Bernstein, B. Rosenfeld. Homogeneous spaces of innite-dimensional Lie algebras and the characteristic classes of foliations. Russ. Math.Surv. 28 (1973), no. 4(172), 103138. [14] B. Buchberger. An Algorithm for Finding the Basis Elements of the Residue Class Ring of a Zero Dimensional Polynomial Ideal. Ph.D. dissertation, University of Innsbruck. 1965. English translation by Michael Abramson in Journal of Symbolic Computation 41 (2006): 471511. [15] A. Cattaneo, P. Mn ev. Remarks on Chern-Simons invariants. Comm. Math. Phys. 293 (2010), no. 3, 803836. [16] M. Chas, D. Sullivan. String Topology. Preprint arXiv:math/9911159v1 [17] K. Costello. Topological conformal eld theories and Calabi-Yau categories. Adv. Math. 210 (2007), no. 1, 165214 [18] V. Drensky. Free algebras and PI-algebras. Graduate course in algebra. Singapore, 2000. 271 pp. [19] S. Elizalde, M. Noy. Consecutive patterns in permutations. Formal power series and algebraic combinatorics (Scottsdale, AZ, 2001). Adv. in Appl. Math. 30 (2003), no. 1-2, 110125. [20] C-H. Eu, T. Schedler. Calabi-Yau Frobenius algebras. J. Algebra 321 (2009), no. 3, 774815 [21] B. Feigin., Characteristic classes of ags of foliations. Funct. Anal. Appl. 9 (1975), no. 4, 4956. [22] B. Feigin, D. Fuchs, I. Gelfand. Cohomology of the Lie algebra of formal vector elds with coecients in its dual space and variations of characteristic classes of foliations. Funct. Anal. Appl. 8 (1974), no. 2, 1329. [23] D. B. Fuks. Cohomology of innite-dimensional Lie algebras. Contemporary Soviet Mathematics. Consultants Bureau, New York, 1986. 339 pp. [24] W. L. Gan. Koszul duality for dioperads. Math. Res. Lett. 10 (2003), no. 1, 109124 [25] E. Getzler. Batalin-Vilkovisky algebras and two-dimensional topological eld theories. Comm. Math. Phys. 159 (1994), no. 2, 265285. [26] E. Getzler. Operads and moduli spaces of genus 0 Riemann surfaces. The moduli space of curves (Texel Island, 1994), 199230, Progr. Math., 129, Boston, MA, 1995. [27] C. Glennie. some identities valid in special Jordan algebras but not valid in all Jordan algebras. Pacic J. Math. 16 1966 4759 [28] V. Ginzburg, M. Kapranov. Koszul duality for operads, Duke Math. J., 76:1 (1994), 203 272. [29] G. Hochschild. Cohomology of restricted Lie algebras. Amer. J. Math. 76, (1954). 555580
[30] E. Hobeck, -homology of algebras over an operad. Algebr. Geom. Topol. 10 (2010), no. 3, 17811806 [31] An. Kirillov. On some quadratic algebras. L. D. Faddeevs Seminar on Mathematical Physics, 91113, Amer. Math. Soc. Transl. Ser. 2, 201, 2000 [32] J. Kock. Frobenius algebras and 2D topological quantum eld theories. London Math. Soc. St. Texts, 59. Cambridge University Press, Cambridge, 2004. 240 pp [33] M. Kontsevich. Operads and motives in deformation quantization. Lett. Math. Phys. 48 (1999), no. 1, 3572 [34] J.-L. Loday, B. Vallette. Algebraic Operads. Latest draft of this book available at http://www-irma.u-strasbg.fr/~loday/PAPERS/JLLBV.pdf [35] M. Mandell. Cochains and homotopy type. Publ. Math. Inst. Hautes Etudes Sci. No. 103 (2006), 213246. [36] S. Merkulov. Operad of formal homogeneous spaces and Bernoulli numbers. Algebra Number Theory 2 (2008), no. 4, 407433, [37] P. Mn ev. Notes on simplicial BF theory. Mosc. Math. J. 9 (2009), no. 2, 371410 [38] A. Polishchuk, L. Positselski. Quadratic algebras. University Lecture Series, 37. American Mathematical Society, Providence, RI, 2005. 159 pp. [39] S. Priddy. Koszul resolutions. Trans. Amer. Math. Soc. 152 1970 3960. [40] D. Quillen. Rational homotopy theory. Ann. of Math. (2) 90, 1969, 205295. [41] D. Quillen. Homotopical algebra. Lecture Notes in Mathematics, No. 43, 1967, 156 pp. [42] G. Segal. Notes of Lectures on eld theories, http://www.cgtp.duke.edu/ITP99/segal/ [43] P. Severa Formality of the chain operad of framed little disks. Lett. Math. Phys. 93 (2010), No. 1, 2935 [44] B. Sturmfels. What is . . . a Gr obner Basis?, Notices of the American Mathematical Society 52 (10): 11991200, http://math.berkeley.edu/ bernd/what-is.pdf, a brief introduction. [45] D. Tamarkin. Another arXiv:math/9803025 proof of M. Kontsevich formality theorem. Preprint
[46] A. Thedy. A natural s-identity of Jordan algebras. Comm. Algebra 15 (1987), no. 10, 2081 2098. [47] V. Ufnarovski. Criterion for the growth of graphs and algebras given by words. Mat. Zametki 31 (1982), no. 3, 465472, 476 [48] V. Ufnarovski. Combinatorial and asymptotic methods in algebra. Algebra, VI, 1196, Encyclopaedia Math. Sci., 57, Springer, Berlin, 1995, [49] P. Van der Laan. Coloured Koszul duality and strongly homotopy operads. Preprint arXiv:math/0312147v2
Você também pode gostar
- Solutions Manual To Algebra, Chapter 0Documento107 páginasSolutions Manual To Algebra, Chapter 0Sheldon Petrus100% (1)
- (Catherine Twomey Fosnot, Bill Jacob) Constructing AlgebraDocumento220 páginas(Catherine Twomey Fosnot, Bill Jacob) Constructing AlgebraFe-humildad Amor-paz EsperanzaAinda não há avaliações
- AL E B A: Teaching School Mathematics: Pre-AlgebraDocumento407 páginasAL E B A: Teaching School Mathematics: Pre-AlgebraBob CrossAinda não há avaliações
- DefQuant FinalDocumento57 páginasDefQuant FinalHuong Cam ThuyAinda não há avaliações
- Applied MathsDocumento13 páginasApplied MathsRex LebanonAinda não há avaliações
- Implementation of Bourbaki's Elements of Mathematics in Coq: Part One, Theory of SetsDocumento48 páginasImplementation of Bourbaki's Elements of Mathematics in Coq: Part One, Theory of Setshelicopter2012Ainda não há avaliações
- Introduction To Quantum GroupsDocumento46 páginasIntroduction To Quantum GroupsEnrique HernandezGarciaAinda não há avaliações
- Markov Partitions and Symbolic DynamicsDocumento56 páginasMarkov Partitions and Symbolic DynamicsGeelonSoAinda não há avaliações
- A Friendly Overview of Noncommutative Geometry-Andrzej SitarzDocumento25 páginasA Friendly Overview of Noncommutative Geometry-Andrzej Sitarznajam u saqibAinda não há avaliações
- Entropy Theory and RAS Are FriendsDocumento20 páginasEntropy Theory and RAS Are FriendsWilliamtomAinda não há avaliações
- Chapter 1Documento18 páginasChapter 1yuvy14Ainda não há avaliações
- AlgProc EssayDocumento5 páginasAlgProc EssayA.S. AAinda não há avaliações
- From Hilbert To Tarski: Gabriel Braun, Pierre Boutry, Julien NarbouxDocumento20 páginasFrom Hilbert To Tarski: Gabriel Braun, Pierre Boutry, Julien NarbouxJoydip SahaAinda não há avaliações
- Report 09 W 5102Documento6 páginasReport 09 W 5102Abir GhoshAinda não há avaliações
- Courcelle 1993Documento34 páginasCourcelle 1993tien.stow.pol.art.muzAinda não há avaliações
- Numerical IntegrationDocumento8 páginasNumerical Integration丨ㄒ丂ᐯ乇ᗪ卂几ㄒAinda não há avaliações
- The Geometry of Graphs and Some of Its Algorithmic ApplicationsDocumento31 páginasThe Geometry of Graphs and Some of Its Algorithmic ApplicationsSergio Andrés UrreaAinda não há avaliações
- Algebraic CombinatoricsDocumento3 páginasAlgebraic CombinatoricsRobin TimkangAinda não há avaliações
- 4 FEM - Lect2Documento113 páginas4 FEM - Lect2sandeepAinda não há avaliações
- Heights and Measures On Analytic Spaces. A Survey of Recent Results, and Some RemarksDocumento41 páginasHeights and Measures On Analytic Spaces. A Survey of Recent Results, and Some RemarksHonciug GeorgeAinda não há avaliações
- Inter-Universal Teichmuller Theory IVDocumento61 páginasInter-Universal Teichmuller Theory IVseanbyramAinda não há avaliações
- Combinatorial Anabelian Topics IIIDocumento97 páginasCombinatorial Anabelian Topics IIIJack Ignacio NahmíasAinda não há avaliações
- From Tarski To HilbertDocumento21 páginasFrom Tarski To HilbertDavid LeonardoAinda não há avaliações
- 1410 7277v1 PDFDocumento14 páginas1410 7277v1 PDFsvante raudersonAinda não há avaliações
- Kozlowski Advancements of FPT in MFS Arab J Math 2012Documento20 páginasKozlowski Advancements of FPT in MFS Arab J Math 2012Walter KozlowskiAinda não há avaliações
- A Quantum Algebraic Topology Framework For Multiscale Quantum ComputationsDocumento11 páginasA Quantum Algebraic Topology Framework For Multiscale Quantum ComputationsRakesh LinAinda não há avaliações
- Sets For Mathematics PDFDocumento276 páginasSets For Mathematics PDFKaizer DAn100% (1)
- VERY - Introduction To The Fock Quantization of The Maxwell FieldDocumento21 páginasVERY - Introduction To The Fock Quantization of The Maxwell FieldahsbonAinda não há avaliações
- TFT Construction of RCFT Correlators V: Proof of Modular Invariance and FactorisationDocumento91 páginasTFT Construction of RCFT Correlators V: Proof of Modular Invariance and Factorisationjsdmf223Ainda não há avaliações
- History: Mathematical Analysis, Which Mathematicians Refer To Simply As Analysis, Has ItsDocumento5 páginasHistory: Mathematical Analysis, Which Mathematicians Refer To Simply As Analysis, Has Itsashi1564Ainda não há avaliações
- Quantum Probability Theory: Mikl Os R Edei and Stephen J. SummersDocumento29 páginasQuantum Probability Theory: Mikl Os R Edei and Stephen J. SummersMojeime Igor NowakAinda não há avaliações
- A Fresh Look at The Bohr - Rosenfeld Analysis and A Proof of A Conjecture of HeisenbergDocumento7 páginasA Fresh Look at The Bohr - Rosenfeld Analysis and A Proof of A Conjecture of HeisenbergahsbonAinda não há avaliações
- Minnes Research 1105 TOCDocumento9 páginasMinnes Research 1105 TOCSaquib ShaikhAinda não há avaliações
- Uspensky Arxiv Ver1Documento23 páginasUspensky Arxiv Ver1Agustín ContrerasAinda não há avaliações
- Two Dimensional Geometric Model: Understanding and Applications in Computer VisionNo EverandTwo Dimensional Geometric Model: Understanding and Applications in Computer VisionAinda não há avaliações
- Coecke (Cat Physics)Documento30 páginasCoecke (Cat Physics)Perita CromagnoliAinda não há avaliações
- (Kailath) - Some New Results in Least-SquaresDocumento42 páginas(Kailath) - Some New Results in Least-SquaresJose Perea ArangoAinda não há avaliações
- The Moi Formula For Improper Algebraic-Exponential IntegralDocumento5 páginasThe Moi Formula For Improper Algebraic-Exponential IntegralFrank Waabu O'Brien (Dr. Francis J. O'Brien Jr.)Ainda não há avaliações
- Minobb Jylanki 2015 06 01 PDFDocumento13 páginasMinobb Jylanki 2015 06 01 PDFHistoric Shi Tpa TownAinda não há avaliações
- J. Chris Eilbeck Et Al - Spectral Curves of Operators With Elliptic CoefficientsDocumento17 páginasJ. Chris Eilbeck Et Al - Spectral Curves of Operators With Elliptic Coefficients23213mAinda não há avaliações
- Donaldson 1989 Connected Sums of Self-Dual Manifolds and Deformations of Singular SpacesDocumento44 páginasDonaldson 1989 Connected Sums of Self-Dual Manifolds and Deformations of Singular SpacesGuido FranchettiAinda não há avaliações
- On The Completeness of Total Spaces of HorizontallDocumento12 páginasOn The Completeness of Total Spaces of HorizontallIbrahim LAKRINIAinda não há avaliações
- Accardi1984 - The Probabilistic Roots of The Quantum Mechanical ParadoxesDocumento34 páginasAccardi1984 - The Probabilistic Roots of The Quantum Mechanical Paradoxespanou dimAinda não há avaliações
- 0304023v1 PDFDocumento69 páginas0304023v1 PDFBayer MitrovicAinda não há avaliações
- Projects MATH61000Documento11 páginasProjects MATH61000janiarun9Ainda não há avaliações
- Notes On Domain Theory by MisloveDocumento33 páginasNotes On Domain Theory by MislovefturingAinda não há avaliações
- Multiplicative Infinite Loop Space Theory: Department of Mathematics. University of Chicago, IL 60637, USADocumento69 páginasMultiplicative Infinite Loop Space Theory: Department of Mathematics. University of Chicago, IL 60637, USAEpic WinAinda não há avaliações
- Geometric AlgebraMASTERDocumento33 páginasGeometric AlgebraMASTERDavid Roberts100% (2)
- Awesome BookDocumento22 páginasAwesome BookSaikat SenguptaAinda não há avaliações
- An Algebraic Exploration of Dominating Sets and Vizing's ConjectureDocumento30 páginasAn Algebraic Exploration of Dominating Sets and Vizing's ConjectureLuis Alberto FuentesAinda não há avaliações
- Multifractal Image Analysis.Documento26 páginasMultifractal Image Analysis.Jack BurtonAinda não há avaliações
- Abstract Poster PDFDocumento21 páginasAbstract Poster PDFMohan Kumar100% (1)
- IntegralDocumento21 páginasIntegralgamerootAinda não há avaliações
- Feynman's Path Integrals and Bohm's Particle PathsDocumento4 páginasFeynman's Path Integrals and Bohm's Particle PathsSantiago PoulainAinda não há avaliações
- Wen You Chen 2020Documento14 páginasWen You Chen 2020HAFIZ LAWAL IBRAHIMAinda não há avaliações
- Repr ExtDocumento23 páginasRepr Extalin444444Ainda não há avaliações
- 1 s2.0 S0747717186800074 MainDocumento10 páginas1 s2.0 S0747717186800074 Mainrandomrandom221Ainda não há avaliações
- Random Walks and Hamronic Functions in Hyperbolic Geometric Group Theory Albert GarretaDocumento21 páginasRandom Walks and Hamronic Functions in Hyperbolic Geometric Group Theory Albert GarretaAlbert GarretaAinda não há avaliações
- Institute of Technology Report On Application of Linear Algebra Even Term 2019-20Documento24 páginasInstitute of Technology Report On Application of Linear Algebra Even Term 2019-20MILAN RAMAinda não há avaliações
- Beginner Guide To Non Commutative GeometryDocumento12 páginasBeginner Guide To Non Commutative GeometryfreimannAinda não há avaliações
- BSMaSS 2 1Documento4 páginasBSMaSS 2 1Daniela Mardini GonzálezAinda não há avaliações
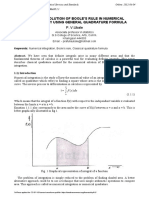
- Numerical Solution of Boole'S Rule in Numerical Integration by Using General Quadrature FormulaDocumento4 páginasNumerical Solution of Boole'S Rule in Numerical Integration by Using General Quadrature Formuladyatlov chernobylAinda não há avaliações
- Density of Diagonalizable Square Matrices: Eigenvector EigenvalueDocumento5 páginasDensity of Diagonalizable Square Matrices: Eigenvector EigenvalueEpic WinAinda não há avaliações
- Eng Math 145 - SummaryDocumento22 páginasEng Math 145 - SummaryHannah Du toitAinda não há avaliações
- Bdwbu: Mshy I HŠWMK KV Yi Wî Kvywgwzk AbycvzDocumento54 páginasBdwbu: Mshy I HŠWMK KV Yi Wî Kvywgwzk Abycvzzisan100% (1)
- Two Dimensional Co-Ordinate GeometryDocumento29 páginasTwo Dimensional Co-Ordinate Geometryshantam777Ainda não há avaliações
- NIMCET Syllabus For MathematicsDocumento2 páginasNIMCET Syllabus For MathematicsDeepak Gupta DpkAinda não há avaliações
- Mathematics: Quarter III-Week 1 Learning Activity Sheets (LAS)Documento8 páginasMathematics: Quarter III-Week 1 Learning Activity Sheets (LAS)Florame Algarme MelanoAinda não há avaliações
- ENG2005 Lecture BookDocumento230 páginasENG2005 Lecture Bookأزيان زكرياAinda não há avaliações
- Inequalities, Algebra Revision Notes From A-Level Maths TutorDocumento4 páginasInequalities, Algebra Revision Notes From A-Level Maths TutorA-level Maths TutorAinda não há avaliações
- MATLAB SlidesDocumento76 páginasMATLAB SlidesShwe LayAinda não há avaliações
- Rayleigh Ritz Method: APL705 Finite Element MethodDocumento4 páginasRayleigh Ritz Method: APL705 Finite Element MethodAshitosh KadamAinda não há avaliações
- Math 9 Q2 Module 3 Final Copy 1Documento16 páginasMath 9 Q2 Module 3 Final Copy 1Hannah LunasAinda não há avaliações
- Methods of DifferentiationDocumento13 páginasMethods of DifferentiationVishruth Reddy BuruguAinda não há avaliações
- Conics and QuadricsDocumento3 páginasConics and QuadricsDarabaGabriellAinda não há avaliações
- s.5 Submathematics End of Term 11 OriginalDocumento3 páginass.5 Submathematics End of Term 11 OriginalNDYAMUSIIMA METHODIUSAinda não há avaliações
- Front MatterDocumento10 páginasFront MatterErnesto D. AguirreAinda não há avaliações
- Chapter 9 - Linear Equation in One Variable (Part - 3), Class 8, Maths RD SharmaDocumento12 páginasChapter 9 - Linear Equation in One Variable (Part - 3), Class 8, Maths RD SharmaSunil AnandAinda não há avaliações
- MATLAB 06 Control StructuresDocumento13 páginasMATLAB 06 Control StructuresHassan AzouzAinda não há avaliações
- June 2019 MSDocumento14 páginasJune 2019 MSpedro pascalAinda não há avaliações
- Cyclic CodesDocumento94 páginasCyclic CodesMariya JohnsonAinda não há avaliações
- Geometric Algebra ThesisDocumento6 páginasGeometric Algebra ThesisJill Brown100% (2)
- A Report On Face Recognition Using Principal Component AnalysisDocumento13 páginasA Report On Face Recognition Using Principal Component AnalysissharibAinda não há avaliações
- Simplification Using K-MapDocumento8 páginasSimplification Using K-MapSiegrique Ceasar A. JalwinAinda não há avaliações
- Applied Mathematics II (E5)Documento2 páginasApplied Mathematics II (E5)eliyasworku2Ainda não há avaliações
- Primitive RootsDocumento11 páginasPrimitive RootsRameez QureshiAinda não há avaliações
- General Mathematics 1Documento18 páginasGeneral Mathematics 1michael delin0% (1)
- MA2401 Lecture NotesDocumento270 páginasMA2401 Lecture NotesJojo LomoAinda não há avaliações
- Differential Equations Computing and Modeling 5th Edition Edwards Solutions ManualDocumento54 páginasDifferential Equations Computing and Modeling 5th Edition Edwards Solutions Manualpseudolatakia.drbn100% (24)