MATH 5311 Advanced Engineering Math

Fourier Series
Deborah Koslover
dkoslover@uttyler.edu
RBN 4010
Section 11.1
Heat distribution in a metal plate,
using Fourier's method
Joseph Fourier
1768-1830
Joseph Fourier French mathematician, physicist and Egyptologist
December 21, 1807 Presented paper to the
Paris Institute, On the Propagation of Heat in
Solid Bodies
Wrote periodic functions as infinite series of trigonometric functions, what
we now call a Fourier series.
Joseph Fourier
Applications of Fourier Analysis
Vibration and Wave Analysis
Electrostatics Problems
Signal and Image Processing
Data Compression
Deducing chemical composition of stars
Optimizing the design of
telecommunications systems
Heat Flow
Optics
Acoustics
Antenna Design and Analysis
Electronic Filter Design and Analysis
X-ray Crystallography Analysis
Copyright 1997 American Physiological Society
Heart rate power spectrum from a
control subject (A) and a patient
suffering from diabetic neuropathy (B).
Frequency peaks are clearly blunted in
the latter (note different power scaling).
A noninvasive, sensitive method for the
early diagnosis of autonomic
neuropathy in diabetes mellitus,
Periodic Functions
Definition: A periodic function is a function that repeats its values on
regularly spaced intervals.
Definition: The interval on which a function repeats is called the period.
Period
Mathematically, we say a function has period p if ( ) ( ) f x p f x + =
x
f (x)
x + p
Notice also that
( ) ( ) 2 , f x p f x + =
x + 2p
( ) ( ) ( ) 1 , f x p f x + =
x - p
and in fact
( ) ( ) , f x np f x + = where n is any nonzero integer.
So a function with period p also has a period of any multiple of p.
Periodic Functions
-6 -4 -2 2 4 6
-1
-0.5
0.5
1
Example: ( ) ( ) cos 2 f x x =
p =
and p = 2
and p = 3

Example: ( ) ( ) ( ) ( ) ( ) ( ) cos , sin , cos 2 , sin 2 , cos 3 , sin 3 , x x x x x x

all have period 2 . p =
Periodic Functions
Constant functions are periodic over arbitrary interval lengths.
-6 -4 -2 2 4 6
0.5
1
1.5
2
Example:
( ) 1 f x =
has period 1, 12, 3.27, 2, or any other value you would like
to choose.
Functions with Period 2
Generally, functions with period 2 can be written in the form of an
infinite sum, as
( ) [ ]
0
1
cos sin
n n
n
f x a a nx b nx
=

= + +

This is called a Fourier series. The as and bs are called Fourier

coefficients.
To be able to use Fourier series to solve problems, we must find the
Fourier coefficients that go with any particular function.
Finding Fourier Coefficients
We will need the following trigonometric identities.
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
1 1
2 2
1 1
2 2
1 1
2 2
cos cos cos cos
sin sin cos cos for , positive integers
sin cos sin sin
nx mx n m x n m x
nx mx n m x n m x n m
nx mx n m x n m x
= + + ( (

= + ( (
`

= + + ( (
)
Integrate each identity from to .
( )
( )
( )
( )
1 1
sin sin
2 2
n m x n m x
n m
m
n
n
m


= + +
+

( ) ( ) ( ) ( )
1 1
2 2
cos cos cos cos nx mx dx n m x dx n m x dx


= + + ( (

( )
( ) ( ) ( )
( )
( ) ( ) ( )
1
sin sin
2
1
sin sin
2
n m n m
n m
n m n m
n m


( = + + ( (

+
( + ( (

0 =
Finding Fourier Coefficients
So if n m then
( ) ( ) cos cos 0 nx mx dx

What if n = m?
( ) ( ) ( ) ( )
1 1
2 2
cos cos cos cos nx nx dx n n x dx n n x dx


= + + ( (

( ) ( ) [ ]
2
1 1
2 2
cos cos 2 cos 0 nx dx nx dx dx


= +

( )
1 1
2 2
cos 2nx dx dx


= +

( )
1
2
1
sin 2
4
nx x
n


= +
( ) ( ) ( ) ( )
1
2
1
sin 2 sin 2
4
n n
n
( = + (

=
Finding Fourier Coefficients
Summarizing,
( ) ( ) cos cos 0 nx mx dx

If n = m, then ( ) ( ) cos cos nx nx dx

Similarly we can show,

if n m, then ( ) ( ) sin sin 0 nx mx dx

if n = m, then
( ) ( ) sin sin nx nx dx

if n m, then
( ) ( ) sin cos 0 nx mx dx

if n = m, then
( ) ( ) sin cos 0 nx nx dx

if n m, then
Using these results, we will
be able to find the Fourier
coefficients.
( ) [ ]
0
1
cos sin
n n
n
f x a a nx b nx
=

= + +

Finding Fourier Coefficients

Given a function f, which has a period of 2, we want to find the Fourier
coefficients so that
Integrate both sides of the equation from to .
( )
0
1
cos sin
n n
n
f x dx a dx a nx dx b nx dx


=

(
= + +
(

Assuming term-wise
integration is allowed.
0
1
sin cos
n n
n
a b
a x nx nx
n n


=

(
= +
(

( ) ( ) ( ) ( ) ( ) ( )
0
1
sin sin cos cos
n n
n
a b
a n n n n
n n

=

(
= +
(

( ) ( )
0
1
2 0 0 cos cos
n n
n
a b
a n n
n n

=

(
= +
(

0
2a =
Dividing both sides by 2
( )
0
1
2
f x dx a

Finding Fourier Coefficients

Now find the other coefficients. Multiply both sides by cos (mx).
( ) [ ]
0
1
cos cos cos cos sin cos
n n
n
f x mx a mx a nx mx b nx mx
=

= + +

( )
0
1
cos cos cos cos sin cos
n n
n
f x mx dx a mx dx a nx mx dx b nx mx dx


=

(
= + +
(

( ) [ ]
0
1
cos sin
n n
n
f x a a nx b nx
=

= + +

Integrate both sides of the equation from to .

Recall
( ) ( ) sin cos 0 nx mx dx

( ) cos
m
f x mx dx a

Recall ( ) ( ) cos cos 0 nx mx dx

If n = m, then ( ) ( ) cos cos nx nx dx

if n m, then
Dividing both sides by , we get
( )
1
cos
m
f x mx dx a

Finding Fourier Coefficients

Multiply both sides by sin (mx).
( ) [ ]
0
1
sin sin cos sin sin sin
n n
n
f x mx a mx a nx mx b nx mx
=

= + +
( )
0
1
sin sin cos sin sin sin
n n
n
f x mx dx a mx dx a nx mx dx b nx mx dx


=

(
= + +
(

( ) [ ]
0
1
cos sin
n n
n
f x a a nx b nx
=

= + +

Integrate both sides of the equation from to .

Recall
( ) ( ) sin cos 0 nx mx dx

( ) sin
m
f x mx dx b

Recall
Dividing both sides by , we get
( )
1
sin
m
f x mx dx b

Now do the same thing with sine.

( ) ( ) sin sin 0 nx mx dx

if n = m, then
( ) ( ) sin sin nx nx dx

if n m, then
Euler Equations
( )
0
1
2
a f x dx

( )
1
cos
m
a f x mx dx

( )
1
sin
m
b f x mx dx

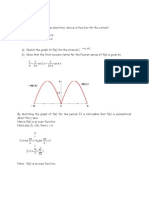
Example: Find the Fourier series for the given f (x), which is assumed to
have the period 2. Graph the partial sums up to that including cos (5x)
and sin (5x).
-

3 4 2 -3 -4 -2 -

First we start by finding a formula for the function.

Between and 0, the function is f (x) = 0.
Between 0 and , the function is a line. It has slope m = -1
and y-intercept b = . Thus, f (x) = -x +
Or
( )
0 if 0
if 0
x
f x
x x

=

+ <

Example: Find the Fourier series for the given f (x), which is assumed to
have the period 2. Graph the partial sums up to that including cos (5x)
and sin (5x).
-

( )
0 if 0
if 0
x
f x
x x

=

+ <

Now apply the Euler equations.

( )
0
1
2
a f x dx

( ) ( )
0
0
1 1
2 2
f x dx f x dx

= +

0
0
1 1
0
2 2
dx x dx

= + +

2 2
2
0
0
1 1
2 2 2 2 4
x
x a

| | | |
= + = + = =
| |
\ \
Example: Find the Fourier series for the given f (x), which is assumed to
have the period 2. Graph the partial sums up to that including cos (5x)
and sin (5x).
-

( )
0 if 0
if 0
x
f x
x x

=

+ <

0
4
a

=
( )
1
cos
m
a f x mx dx

( ) ( )
0
0
1 1
cos cos f x mx dx f x mx dx

= +

( )
0
1
cos x mx dx

= +
1
cos
sin
m
u x dv mx dx
du dx v mx
= + =
= =
Integrating by parts
0
0
1 1
sin sin
x
mx mx dx
m m

(
+
= +
(

0
1
sinmx dx
m

( )
1 if is even
cos
-1 if is odd
1 if is even
-1 if is odd
1
m
m
m
m
m
m
=

Notice
( )
2 2 0
1 1
cos cos cos0 mx m
m m

= =
( )
( )
2
1
1 1
m
m
a
m

= =
Example: Find the Fourier series for the given f (x), which is assumed to
have the period 2. Graph the partial sums up to that including cos (5x)
and sin (5x).
-

( )
0 if 0
if 0
x
f x
x x

=

+ <

0
4
a

=
( )
( )
2
1
1 1
m
m
a
m

=
Similarly, integrating by parts, we can show that
1
m
b
m
=
So, the Fourier series for f (x) is
( ) [ ]
( )
( )
0
1
2
1
cos sin
1 1
1 1 cos sin
4
m m
m
m
m
f x a a mx b mx
mx mx
m m

=
=

= + +
(
= + +
(

2 1 2 1
cos sin sin2 cos3 sin3
4 2 9 3
1 2 1
sin4 cos5 sin5 ...
4 25 5
x x x x x
x x x

= + + + + +
+ + +
-3 -2 -1 1 2 3
0.5
1
1.5
2
2.5
-3 -2 -1 1 2 3
0.5
1
1.5
2
2.5
-3 -2 -1 1 2 3
0.5
1
1.5
2
2.5
-3 -2 -1 1 2 3
0.5
1
1.5
2
2.5
-3 -2 -1 1 2 3
0.5
1
1.5
2
-3 -2 -1 1 2 3
0.25
0.5
0.75
1
1.25
1.5
Partial Sums
-

( )
2 1 2 1
cos sin sin 2 cos3 sin3
4 2 9 3
1 2 1
sin4 cos5 sin5 ...
4 25 5
f x x x x x x
x x x

= + + + + +
+ + +
5
2 1 2
cos sin sin 2 cos 3
4 2 9
1 1 2 1
sin 3 sin 4 cos 5 sin 5
3 4 25 5
p x x x x
x x x x

= + + + +
+ + + +
4
2 1
cos sin sin 2
4 2
2 1 1
cos 3 sin 3 sin 4
9 3 4
p x x x
x x x

= + + +
+ + +
3
2 1
cos sin sin 2
4 2
2 1
cos 3 sin 3
9 3
p x x x
x x

= + + +
+ +
2
2 1
cos sin sin 2
4 2
p x x x

= + + +
1
2
cos sin
4
p x x

= + +
0
4
p

=
http://math.furman.edu/~dcs/java/square.html
Convergence of Fourier Series
Theorem: Let f (x) be periodic with period 2 and piecewise continuous
on the interval - x .
A function is piecewise continuous if it is only discontinuous at a finite
number of points.
Further, let f (x) have a left hand derivative and
a right hand derivative at every point of that interval.
( ) ( ) ( ) ( )
0 0
lim and lim exist
h h
f x h f x f x h f x
h h
+

+ +
Then the Fourier
is discontinuous. There the sum is the average of the left and right
hand limit of f (x) at x
0
.
-

2 -2 -

f (x)
-

2 -2 -

[ ]
0
1
cos sin
n n
n
a a nx b nx
=

+ +

series of f (x) converges. Its sum is f (x) except at points x

0
where f (x)
Energy Spectrum for the Flute and Violin
MATH 5311 Advanced Engineering Math
Functions of Any Period p = 2L
Section 11.2
Fourier Series for functions of period p = 2L
3 4 2 -3 -4 -2 -
How would we find the formula for the Fourier series for this function?
Rescale!
L 3L 4L 2L -3L -4L -2L -L
Find comparable positions of each graph.
y
x
Use ratios.
2
2
L y
x
= or x y
L

=
Fourier Series for functions of period p = 2L
L 2L
y
2
x
x y
L

=
Old system New system
( ) [ ]
0
1
cos sin
n n
n
f x a a nx b nx
=

= + +

( )
0
1
2
a f x dx

( )
1
cos
n
a f x nx dx

( )
1
sin
n
b f x nx dx

dx dy
L

=
0
1
cos sin
n n
n
n n
a a y b y
L L

=

(
= + +
(

f y
L

| |
|
\
( ) f y
0
1
2
L
L
a f y dy
L L

| |
=
|
\

1
cos
L
n
L
a f y n y dy
L L L

| | | |
=
| |
\ \

1
sin
L
n
L
b f y n y dy
L L L

| | | |
=
| |
\ \

( )
1
2
L
L
f y dy
L

( )
1
cos
L
L
n
f y y dy
L L

| |
=
|
\

( )
1
sin
L
L
n
f y y dy
L L

| |
=
|
\

Fourier Series for functions of period p = 2L

( )
0
1
cos sin
n n
n
n n
f x a a x b x
L L

=

(
= + +
(

( )
0
1
2
L
L
a f x dx
L

( )
1
cos
L
n
L
n
a f x x dx
L L

| |
=
|
\

( )
1
sin
L
n
L
n
b f x x dx
L L

| |
=
|
\

1 -1
Example
Find the Fourier series for on the interval ( ) f x x = 1 1 x < <
1
3 4 2 -3 -4 -2
p = 2L
p = 2, so L = 1
( )
if 0
if 0
x x
f x
x x
<
=

( )
0
1
2
L
L
a f x dx
L

( )
1
1
1
2
f x dx

( ) ( )
0 1
1 0
1 1
2 2
f x dx f x dx

= +

( )
0 1
1 0
1 1
2 2
x dx x dx

= +

0 1
2 2
1 0
1 1 1
4 4 4 4 2
x x

= + = + =
Example
Find the Fourier series for on the interval ( ) f x x = 1 1 x < <
1 -1
1
0
1
2
a =
( )
1
cos
L
n
L
n
a f x x dx
L L

| |
=
|
\

( ) ( )
1
1
cos f x n x dx

( ) ( )
0 1
1 0
cos cos x n x dx x n x dx

= +

1
cos
sin
n
u x dv n x dx
du dx v n x

= =
= =
( ) ( )
0 1
0 1
1 1 1 1
1 0
1 0
sin sin sin sin
n n n n
x n x n x dx x n x n x dx

| | | |
= +
| |
\ \

( ) ( )
0 1
1 1
1 0
sin sin
n n
n x dx n x dx

=

( ) ( ) 2 2 2 2
0 1
1 1
1 0
cos cos
n n
n x n x

= +
( ) ( ) 2 2 2 2 2 2 2 2
2 2 2 2
cos 1
n
n n n n
n

= =
Example
Find the Fourier series for on the interval ( ) f x x = 1 1 x < <
1 -1
1
0
1
2
a =
( )
2 2 2 2
2 2
1
n
n
n n
a

=
Integrating, using integration by parts, we can
show similarly that 0
n
b =
So, ( )
( )
( )
( )
0
1
1
2 2 2 2
2 2
cos sin
1
1 cos 0 sin
2
n n
n
n
n
n n
n n
f x a a x b x
L L
n x n x



=
=

(
= + +
(

(
= + +

( )
( )
1
2 2 2 2
2 2
1
1 cos
2
n
n
n n
n x

(
= +

2 2 2
1 4 4 4
cos cos3 cos5
2 9 25
x x x

=
Theorem
Let f
1
and f
2
be functions with period p and let c be a scalar. Then
1) The Fourier coefficients of a sum f
1
+ f
2
are the sums of the Fourier
coefficients of f
1
and of f
2
.
Example If
1
2 4 4 4
cos 2 cos 4 cos 6
3 15 35
f x x x

=
-6 -4 -2 2 4 6
0.2
0.4
0.6
0.8
1
-6 -4 -2 2 4 6
0.2
0.4
0.6
0.8
1
2
1 1 2 2 2
sin cos 2 cos 4 cos6
2 3 15 35
f x x x x

= +
Then
1 2
2 1 1 4 2 4 2
sin cos 2 cos 4
2 3 3 15 15
4 2
cos 6
35 35
f f x x x
x


| | | | | |
+ = + + + +
| | |
\ \ \
| |
+
|
\

1 2
3 1 6 6 6
sin cos 2 cos 4 cos 6
2 3 15 35
f f x x x x

+ = +
-6 -4 -2 2 4 6
0.2
0.4
0.6
0.8
1
f
1
f
2
f
1 +
f
2
Theorem (cont.)
Let f
1
and f
2
be functions with period p and let c be a scalar. Then
2) The Fourier coefficients of cf
1
are c times the Fourier coefficients of f
1
.
We showed
1 -1
1
( )
2 2 2
1 4 4 4
cos cos 3 cos 5
2 9 25
f x x x x

=
1 -1
1
2
( ) 2 f x
2 2 2
8 8 8
1 cos cos3 cos5
9 25
x x x

=
Example
1 -1
1/2
-1/2
How do we find the Fourier series of ?
1 -1
1/2
-1/2
=
1 -1
1
- 1/2
The Fourier series for -1/2 is -1/2.
So the Fourier series is
( )
2 2 2
2 2 2
1 4 4 4 1
cos cos 3 cos5
2 9 25 2
4 4 4
cos cos 3 cos 5
9 25
g x x x x
x x x




| |
=
|
\
=

g(x)