54

Captulo 3: Transformaciones Geomtricas

En matemticas, nunca entiendes las cosas, slo te acostumbras a ellas.
John von Newmann

En este captulo se hace un breve repaso de transformaciones geomtricas 2D y 3D
que son ampliamente conocidas y su extensin a otras dimensiones. Existen varias
transformaciones geomtricas, pero slo se revisan el escalamiento, la translacin y la
rotacin. Se analizan las analogas que hay de estas transformaciones para llevarlas a 4D y
su generalizacin a cualquier espacio nD, poniendo mayor nfasis en la rotacin, donde se
presenta una de las contribuciones de este trabajo, definiendo las matrices generales de IDA
y REGRESO para llevar a cabo las rotaciones alrededor de un eje de rotacin en un espacio
n-dimensional.
En la mayora de los libros y trabajos relacionados con transformaciones geomtricas,
se revisan estos temas organizndolos en orden de dimensiones, es decir, primero se
explican todas las transformaciones 2D y enseguida las transformaciones 3D. En este
trabajo se propone un orden distinto, donde primero se explican los temas por
transformacin, es decir, primero se explica la transformacin de escalamiento en todas sus
dimensiones, enseguida la translacin y por ltimo la rotacin. Esta idea es con la intensin
de darle al lector un mejor entendimiento de las extensiones de las trasformaciones 2D a 3D
y a dimensiones superiores.
3.1 Representacin Matricial y Coordenadas Homogneas
En el rea de la graficacin por computadora, es comn encontrar la representacin de
las ecuaciones de trasformacin por medio de matrices, y se pueden encontrar dos tipos de
55
notaciones para representarlas, una es representando las coordenadas de un punto p como
vectores rengln, en este caso una matriz de transformacin M en 2D, multiplica al punto
por la derecha para obtener el nuevo punto p'.
[ ]
2 1
x x p = , [ ] M p x x p = =
2 1
'
La segunda notacin es representando las coordenadas de un punto p como vectores
columna, en este caso una matriz de transformacin M, multiplica al punto por la izquierda
para obtener el nuevo punto p'.

=
2
1
x
x
p , p M
x
x
p =

=
'
'
'
2
1

En este trabajo, se representan los puntos por medio de vectores rengln, por lo tanto
las matrices de transformacin estarn modeladas para multiplicarlas por la derecha, sin
embargo se puede obtener una matriz de transformacin en la otra notacin calculando su
transpuesta.
No todas las transformaciones son aplicadas a un punto como una multiplicacin de
factores, por tal razn se utilizan las coordenadas homogneas para la representacin
matricial, y de esta forma todas las transformaciones son tratadas como multiplicaciones.
En coordenadas homogneas, a cada punto 2D se le agrega una tercera coordenada, de
esta forma, en lugar de representar los puntos como ) , (
2 1
x x p = son representados como
una terna ) , , (
2 1
x x p = , al mismo tiempo se dice que un par de coordenadas homogneas
) , , (
2 1
x x y ) ' , ' , ' (
2 1
x x representan el mismo punto si una es mltiplo de la otra. Por
ejemplo, la terna (4, -2, 6) y (8, -4, 12) representan el mismo punto 2D pero en diferentes
coordenadas triples, esto significa que cada punto tiene un sinfn de representaciones en
coordenadas homogneas.
56
Al menos uno de las coordenadas homogneas tiene que ser distinta de cero, por lo
tanto la terna (0, 0, 0) no es vlida. Si la coordenada 0, la terna ) , , (
2 1
x x se puede
dividir entre y se obtiene ) 1 , , (
2 1
x x , cuando se realiza esta divisin, a los valores
x
1
/ y x
2
/ se les llama coordenadas cartesianas del punto homogneo [Foley 92]. Una
eleccin conveniente es hacer el valor de = 1, as cada posicin 2D es representada con
las coordenadas homogneas ) 1 , , (
2 1
x x . A los puntos con la forma ) 0 , , (
2 1
x x se les llama
puntos al infinito, los cuales no se tratarn en esta investigacin.
En general para cualquier dimensin las coordenadas homogneas de un punto p en
nD se escribe como ) , , , , (
2 1

n
x x x p K = , el cul es un vector de longitud n+1.
3.2 Extensin de las Transformaciones a Otras Dimensiones
Las trasformaciones geomtricas 3D son extensiones de las transformaciones
geomtricas 2D, pero con la incorporacin del eje Z [Hearn 95]. En [Hollasch, 91] se
muestra que los puntos y operaciones vectoriales en el espacio 4D son simples extensiones
de su contraparte 3D.
Como se ver enseguida, muchas de las operaciones matemticas utilizadas en las
transformaciones de escalamiento y translacin se extienden fcilmente, pero la rotacin no
es tan intuitiva y requiere de un poco ms de anlisis, para comprender su generalizacin a
otras dimensiones.
3.3 Escalamiento
El escalamiento permite cambiar el tamao de un objeto expandindolo o
contrayndolo en sus dimensiones.
57
3.3.1 Escalamiento 2D
El escalamiento 2D implica el cambio de tamao de un polgono, donde cada punto
) , (
2 1
x x p = es transformado por la multiplicacin de dos factores de escalamiento: s
1
y s
2
a
lo largo de los ejes X
1
y X
2
respectivamente, de esta forma, las coordenadas del nuevo punto
) ' , ' ( '
2 1
x x p = se obtienen como:
2 2 2
1 1 1
'
'
s x x
s x x
=
=

Sea ) , (
2 1
s s s = el vector de factores de escalamiento, y S(s) la matriz de
escalamiento, en coordenadas homogneas el escalamiento de un punto p en 2D se puede
expresar como el producto matricial ) ( ' s S p p = , es decir:
[ ] [ ]

=
1 0 0
0 0
0 0
1 1 ' '
2
1
2 1 2 1
s
s
x x x x
Ecuacin 3.1: Expresin matricial para el escalamiento 2D.
La Figura 3.1 muestra el efecto de escalamiento de una figura con s
1
= 1.5 y s
2
= 2.

Figura 3.1: Ejemplo de escalamiento 2D.
X
1
X
2

1
2
3
4
5
1 2 3 4 5
X
1

X
2

1
2
3
4
5
1 2 3 4 5
58
3.3.2 Escalamiento 3D
Extendiendo la idea anterior a 3D, el escalamiento implica el cambio de tamao de un
poliedro, donde cada punto ) , , (
3 2 1
x x x p = es transformado por la multiplicacin de tres
factores de escalamiento: s
1
, s
2
y s
3
a lo largo de los ejes X
1
, X
2
y X
3
respectivamente, de
esta forma, las coordenadas del nuevo punto ) ' , ' , ' ( '
3 2 1
x x x p = se obtienen como:
3 3 3
2 2 2
1 1 1
'
'
'
s x x
s x x
s x x
=
=
=

Sea ) , , (
3 2 1
s s s s = el vector de factores de escalamiento, y S(s) la matriz de
escalamiento, en coordenadas homogneas el escalamiento de un punto p en 3D se puede
expresar como el producto matricial ) ( ' s S p p = , es decir:
[ ] [ ]

=
1 0 0 0
0 0 0
0 0 0
0 0 0
1 1 ' ' '
3
2
1
3 2 1 3 2 1
s
s
s
x x x x x x
Ecuacin 3.2: Expresin matricial para el escalamiento 3D.
La Figura 3.2 muestra el efecto de escalamiento de una figura con s
1
= 2, s
2
= 2.5 y
s
3
= 1.5.
59

Figura 3.2: Ejemplo de escalamiento 3D.
3.3.3 Escalamiento 4D
Extendiendo nuevamente la idea anterior a 4D, el escalamiento implica el cambio de
tamao de un politopo 4D, donde cada punto ) , , , (
4 3 2 1
x x x x p = es transformado por la
multiplicacin de cuatro factores de escalamiento: s
1
, s
2
, s
3
y s
4
a lo largo de ejes que
forman el espacio 4D, de esta forma, las coordenadas del nuevo punto
) ' , ' , ' , ' ( '
4 3 2 1
x x x x p = se obtienen como:
4 4 4
3 3 3
2 2 2
1 1 1
'
'
'
'
s x x
s x x
s x x
s x x
=
=
=
=

Sea ) , , , (
4 3 2 1
s s s s s = el vector de factores de escalamiento, y S(s) la matriz de
escalamiento, en coordenadas homogneas el escalamiento de un punto p en 4D se puede
expresar como el producto matricial ) ( ' s S p p = , es decir:
X
1

X
2

1
2
3
4
5
1 2 3 4 5
X
3


1
2
3
4
5
X
1

X
2


1
2
3
4
5
1 2 3 4 5
X
3

1
2
3
4
5
60
[ ] [ ]

=
1 0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
1 1 ' ' ' '
4
3
2
1
4 3 2 1 4 3 2 1
s
s
s
s
x x x x x x x x
Ecuacin 3.3: Expresin matricial para el escalamiento 4D.
3.3.4 Escalamiento nD
De esta forma, el escalamiento nD implica el cambio de tamao de un politopo nD en
todas sus dimensiones, como se observ anteriormente, se puede representar el
escalamiento nD en su forma matricial, donde los factores de escalamiento se localizan en
la diagonal principal, cada uno colocado en la columna que le corresponde a su respectivo
eje. As, se obtiene la expresin matricial de escalamiento para cualquier dimensin:
[ ] [ ]

=
1 0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
1 1 ' ' ' '
3
2
1
3 2 1 3 2 1
K
K
M M O M M M
K
K
K
K K
n
n n
s
s
s
s
x x x x x x x x
Ecuacin 3.4: Expresin matricial para el escalamiento nD.
En general, la matriz de escalamiento S(s) para nD en coordenadas homogneas
tendr un tamao de (n+1) (n+1), en la cual, si se sustituyen los valores para n=2 y n=3,
se obtienen las matrices de escalamiento 2D y 3D respectivamente.
3.4 Translacin
La translacin permite desplazar un objeto a lo largo de sus dimensiones, como
resultado se obtiene un cambio de posicin.
61
3.4.1 Translacin 2D
La translacin 2D implica el desplazamiento de un polgono, donde cada punto
) , (
2 1
x x p = es trasladado d
1
unidades en el eje X
1
y d
2
unidades en el eje X
2
, de esta forma,
las coordenadas del nuevo punto ) ' , ' ( '
2 1
x x p = , se obtienen como:
2 2 2
1 1 1
'
'
d x x
d x x
+ =
+ =

Sea ) , (
2 1
d d d = el vector de distancias, y T(d) la matriz de translacin, en
coordenadas homogneas la translacin de un punto p en 2D se puede expresar como el
producto matricial ) ( ' d T p p = , es decir:
[ ] [ ]

=
1
0 1 0
0 0 1
1 1 ' '
2 1
2 1 2 1
d d
x x x x
Ecuacin 3.5: Expresin matricial para la translacin 2D.
La Figura 3.3 muestra el efecto de translacin de una figura con d
1
= 1 y d
2
= 2.

Figura 3.3: Ejemplo de translacin 2D.
3.4.2 Translacin 3D
Basndose en la idea anterior, se tiene que la translacin 3D implica el
desplazamiento de un poliedro, donde cada punto ) , , (
3 2 1
x x x p = es trasladado d
1
unidades
X
1

X
2

1
2
3
4
5
1 2 3 4 5
X
1

X
2

1
2
3
4
5
1 2 3 4 5
62
en el eje X
1
, d
2
unidades en el eje X
2
y d
3
unidades en el eje X
3
, de esta forma, las
coordenadas del nuevo punto ) ' , ' , ' ( '
3 2 1
x x x p = se obtienen como:
3 3 3
2 2 2
1 1 1
'
'
'
d x x
d x x
d x x
+ =
+ =
+ =

Sea ) , , (
3 2 1
d d d d = el vector de distancias, y T(d) la matriz de translacin, en
coordenadas homogneas la translacin de un punto p en 3D se puede expresar como el
producto matricial ) ( ' d T p p = , es decir:
[ ] [ ]

=
1
0 1 0 0
0 0 1 0
0 0 0 1
1 1 ' ' '
3 2 1
3 2 1 3 2 1
d d d
x x x x x x
Ecuacin 3.6: Expresin matricial para la translacin 3D.
La Figura 3.4 muestra el efecto de translacin de una figura con d
1
= 2, d
2
= 0 y d
3
= 2.

Figura 3.4: Ejemplo de translacin 3D.
X
1

X
2

1
2
3
4
5
1 2 3 4 5
X
3

1
2
3
4
5
X
1

X
2

1
2
3
4
5
1 2 3 4 5
X
3

1
2
3
4
5
63
3.4.3 Translacin 4D
Nuevamente tomando como base esta idea, se tiene que la translacin 4D implica el
desplazamiento de un politopo 4D, donde cada punto ) , , , (
4 3 2 1
x x x x p = es trasladado por
la suma de cuatro distancias: d
1
, d
2
, d
3
, d
4
a cada uno de los ejes que forman el espacio 4D,
de esta forma, las coordenadas del nuevo punto ) ' , ' , ' , ' ( '
4 3 2 1
x x x x p = se obtiene como:
4 4 4
3 3 3
2 2 2
1 1 1
'
'
'
'
d x x
d x x
d x x
d x x
+ =
+ =
+ =
+ =

Sea ) , , , (
4 3 2 1
d d d d d = el vector de distancias, y T(d) la matriz de translacin, en
coordenadas homogneas la translacin de un punto p en 4D se puede expresar como el
producto matricial ) ( ' d T p p = , es decir:
[ ] [ ]

=
1
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1
1 1 ' ' ' '
4 3 2 1
4 3 2 1 4 3 2 1
d d d d
x x x x x x x x
Ecuacin 3.7: Expresin matricial para la translacin 4D.
3.4.4 Translacin nD
De esta forma, la translacin nD implica el desplazamiento de un politopo nD
sumando parmetros de distancias a todas sus dimensiones, como se observ anteriormente,
se puede representar la translacin nD en su forma matricial, donde los parmetros de
distancia se localizan en el ltimo rengln de la matriz, cada uno colocado en la columna
que le corresponde a su respectivo eje, y colocando valores de 1 en la diagonal principal.
As, se obtiene la expresin matricial de translacin para cualquier dimensin:
64
[ ] [ ]

=
1
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1
1 1 ' ' ' '
3 2 1
3 2 1 3 2 1
n
n n
d d d d
x x x x x x x x
K
K
M M O M M M
K
K
K
K K
Ecuacin 3.8: Expresin matricial para la translacin nD.
En general, la matriz de translacin T(d) para nD en coordenadas homogneas tendr
un tamao de (n+1) (n+1), en la cual, si se substituyen los valores para n=2 y n=3, se
obtienen las matrices de translacin 2D y 3D respectivamente.
3.5 Rotacin
La rotacin permite girar un objeto sobre un eje de rotacin, dado un valor de ngulo
de rotacin y su direccin.
3.5.1 Rotaciones 2D
La rotacin de un objeto en 2D se lleva a cabo alrededor de un punto, que es el eje
puntual (cero-dimensional) de rotacin. Las rotaciones principales 2D son aquellas que se
llevan a cabo alrededor del origen, las rotaciones sobre cualquier otro punto arbitrario se
llaman rotaciones generales 2D. En esta Seccin 3.5 , se analizan slo las rotaciones
principales para todas las dimensiones, en la Seccin 3.6 se discuten las rotaciones
generales.
Para generar una rotacin, se especifica el ngulo de rotacin , y el punto de rotacin
(pivote) sobre el cul el objeto ser rotado. Los ngulos de rotacin positivos definen una
rotacin en sentido contrario a las manecillas del reloj sobre el punto pivote (del eje X
1
al
eje X
2
), entonces los ngulos de rotacin negativos producen una rotacin en el sentido de
65
las manecillas (del eje X
2
al eje X
1
). [Hearn 95] describe la rotacin 2D como el giro sobre
el eje de rotacin que es perpendicular al plano X
1
X
2
(mejor conocido como plano XY) y
que pasa a travs del punto pivote.
Si el punto pivote se encuentra sobre el origen (Figura 3.5), se tiene que: r es la
distancia del punto ) , (
2 1
x x p = al origen, define la posicin angular del punto p desde la
horizontal, y el ngulo de rotacin de p para producir el nuevo punto ) ' , ' ( '
2 1
x x p = .

Figura 3.5: Rotacin de un punto en 2D alrededor del origen.
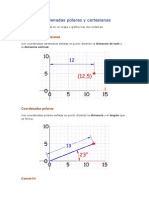
Utilizando coordenadas polares, el punto ) , (
2 1
x x p = se puede escribir como
) , ( r p = y el punto ) ' , ' ( '
2 1
x x p = como ) , ( ' + = r p . Pasando despus estos puntos de
coordenadas polares a rectangulares se tiene que:
) cos(
1
r x = ) sin(
2
r x =
) cos( '
1
+ = r x ) sin( '
2
+ = r x
Aplicando algunas propiedades trigonomtricas:
sin sin cos cos ) cos( '
1
r r r x = + =
cos sin sin cos ) sin( '
2
r r r x + = + =
Substituyendo los valores de ) cos(
1
r x = y ) sin(
2
r x = se obtienen las ecuaciones para
rotar un punto ) , (
2 1
x x p = alrededor del origen dado un ngulo :

X
1

X
2

p=(x
1
,x
2
)
p=(x
1
,x
2
)

r
r
66

Ecuacin 3.9: Frmulas para la rotacin 2D alrededor del origen.
Sea R() la matriz de rotacin sobre el origen, en coordenadas homogneas la
rotacin de un punto p alrededor del origen en 2D se puede expresar como el producto
matricial ) ( ' R p p = , es decir:
[ ] [ ]

=
1 0 0
0 cos sin
0 sin cos
1 1 ' '
2 1 2 1


x x x x
Ecuacin 3.10: Expresin matricial para la rotacin 2D.
La Figura 3.6 muestra el efecto de rotacin de una figura con = 45.

Figura 3.6: Ejemplo de rotacin 2D.
3.5.2 Rotaciones 3D
A diferencia de la rotacin en el espacio 2D, donde para hacer rotar un objeto se
necesita un punto (cero-dimensional), en 3D para hacer rotar un objeto se necesitan dos
puntos no coincidentes que determinan un segmento de recta, cuya lnea de soporte define
un eje lineal (uni-dimensional) de rotacin.
X
1

-1 -2 1 2
X
2

-2
-1
1
2
X
1

-1 -2 1 2
X
2

-2
-1
1
2
sin cos '
2 1 1
x x x =
cos sin '
2 1 2
x x x + =
67
Las rotaciones principales 3D, son aquellas cuando el eje de rotacin se encuentra
sobre alguno de los tres ejes principales: X
1
, X
2
o X
3
, las rotaciones sobre cualquier otro eje
arbitrario son llamadas rotaciones generales 3D. Se recuerda que inicialmente, se analizan
las rotaciones principales.
Por convencin, los ngulos de rotacin positivos producen rotaciones en contra de
las manecillas del reloj sobre el eje de rotacin, esto es si se observa el giro desde la parte
positiva del eje hacia el origen. Otra forma de determinar la direccin de un giro positivo es
mediante la regla de la mano derecha (Figura 3.7), que dice que: Si se coloca el dedo
pulgar de la mano derecha sobre el eje de rotacin apuntando hacia la parte positiva de
dicho eje, el giro natural del resto de los dedos indica la direccin positiva del giro.

Figura 3.7: Regla de la mano derecha para obtener la direccin de un giro positivo en 3D.
Para entender el concepto de rotacin en 3D como una extensin de la rotacin 2D,
hay que recordar que la rotacin 2D es el giro sobre el eje de rotacin, que es perpendicular
al plano X
1
X
2
, el cual en 3D corresponde al eje X
3
, entonces se tiene la primera de las
rotaciones principales [Hearn 95].
De esta forma, por cada punto ) , , (
3 2 1
x x x p = dado un ngulo , puede ser rotado
sobre el eje X
3
en sentido contrario a las manecillas del reloj, obteniendo las coordenadas
del nuevo punto ) ' , ' , ' ( '
3 2 1
x x x p = de la misma forma en como se analiz en el espacio 2D
X
3

X
1

X
2

X
3

X
1

X
2

X
3

X
1

X
2

68
(ver Seccin 3.5.1 ), quedando la coordenada x
3
sin cambio, entonces, se extienden las
formulas para la rotacin 2D (Ecuacin 3.9) a 3D como: [Hearn 95]

Ecuacin 3.11: Frmulas para la rotacin 3D alrededor del eje X
3
.
Sea R
3
() la matriz de rotacin alrededor del eje X
3
, en coordenadas homogneas la
rotacin de un punto p alrededor de dicho eje, se puede expresar como el producto matricial
) ( '
3
R p p = , es decir:
[ ] [ ]

=
1 0 0 0
0 1 0 0
0 0 cos sin
0 0 sin cos
1 1 ' ' '
3 2 1 3 2 1


x x x x x x
Ecuacin 3.12: Expresin matricial para la rotacin 3D alrededor del eje X
3
.
La Figura 3.8 muestra el efecto de rotacin sobre el eje X
3
de una figura con = 20.

Figura 3.8: Ejemplo de rotacin 3D sobre el eje X
3
.
X
1

X
2

1
2
3
4
5
1 2 3 4 5
X
3

1
2
3
4
5
X
1

X
2

1
2
3
4
5
1 2 3 4 5
X
3

1
2
3
4
5
cos sin '
2 1 2
x x x + =
sin cos '
2 1 1
x x x =
3 3
' x x =
69
Las ecuaciones para las rotaciones sobre el eje X
1
, y eje X
2
, pueden ser obtenidas
mediante las permutaciones cclicas de los parmetros x
1
, x
2
, x
3
: [Hearn 95].
x
1
x
2
x
3
x
1

como se muestra en la Figura 3.9

Figura 3.9: Permutaciones cclicas de los ejes coordenados [Hearn 95].
Entonces, aplicando estas substituciones cclicas en la Ecuacin 3.11, se obtienen las
ecuaciones para la rotacin alrededor del eje X
1
dado un ngulo .

Ecuacin 3.13: Frmulas para la rotacin 3D alrededor del eje X
1
.
Sea R
1
() la matriz de rotacin alrededor del eje X
1
, en coordenadas homogneas la
rotacin de un punto p alrededor de dicho eje, se puede expresar como el producto matricial
) ( '
1
R p p = , es decir:
[ ] [ ]

=
1 0 0 0
0 cos sin 0
0 sin cos 0
0 0 0 1
1 1 ' ' '
3 2 1 3 2 1


x x x x x x
Ecuacin 3.14: Expresin matricial para la rotacin 3D alrededor del eje X
1
.
1 1
' x x =
sin cos '
3 2 2
x x x =
cos sin '
3 2 3
x x x + =
sin cos '
3 2 2
x x x =
1 1
' x x =
cos sin '
3 2 3
x x x + =
X
1

X
2

X
3

X
2

X
3

X
1

X
3

X
1

X
2

70
Aplicando nuevamente las substituciones cclicas en la Ecuacin 3.13, se obtienen las
frmulas para la rotacin alrededor del eje X
2
dado un ngulo .

Ecuacin 3.15: Frmulas para la rotacin 3D alrededor del eje X
2
.
Sea R
2
() la matriz de rotacin alrededor del eje X
2
, en coordenadas homogneas la
rotacin de un punto p alrededor de dicho eje, se puede expresar como el producto matricial
) ( '
2
R p p = , es decir:
[ ] [ ]

=
1 0 0 0
0 cos 0 sin
0 0 1 0
0 sin 0 cos
1 1 ' ' '
3 2 1 3 2 1


x x x x x x
Ecuacin 3.16: Expresin matricial para la rotacin 3D alrededor del eje X
2
.
3.5.2.1 Entendiendo las Rotaciones 3D Como Rotaciones Paralelas a un Plano
Las rotaciones en el espacio 3D son bien conocidas y entendidas por la mayora de la
gente, y muchos pueden interpretarla como la rotacin de un objeto alrededor de un eje
(uni-dimensional) de rotacin, sin embargo, es ms adecuado pensar en un conjunto de
rotaciones paralelas a un plano 2D, inmerso en el espacio [Noll 67], esto es til para
comprender ms fcil la analoga en las rotaciones 4D y superiores.
Se sabe que en 3D hay tres ejes coordenado: X
1
, X
2
y X
3
, y los planos principales son
los formados por todas las posibles combinaciones de 2 de estos ejes, se obtienen as, los
planos principales 3D: X
1
X
2
, X
1
X
3
y X
2
X
3
(Figura 3.10).
cos sin '
1 3 1
x x x + =
sin cos '
1 3 3
x x x =
2 2
' x x =
sin cos '
3 1 1
x x x + =
2 2
' x x =
cos sin '
3 1 3
x x x + =
71

Figura 3.10: Planos principales 3D: a) plano X
1
X
2
, b) plano X
1
X
3
y c) plano X
2
X
3
.
Se sabe que hay tres rotaciones principales, que son alrededor de cada uno los ejes
principales, y durante estos giros se cumple que: dado el origen y ngulo de rotacin, el
conjunto de todos los puntos rotados por una matriz dada caen en un plano, llamado plano
de rotacin, y el eje lineal de rotacin es el que coincide con el vector normal de este plano.
Esto es consiste con el espacio 2D, porque todos los puntos rotados caen en un nico y
mismo plano, el plano X
1
X
2
[Hollasch, 91].
Entonces se tiene que las rotaciones alrededor de los ejes coordenados producen
rotaciones de todos los planos paralelos al plano de rotacin, el cul est formado por los
ejes restantes, es decir, si el eje de rotacin es el eje X
3
, el plano de rotacin ser el formado
por los ejes coordenados restantes: el plano X
1
X
2
, de esta manera, si el eje de rotacin es el
eje X
2
, el plano de rotacin ser el plano X
1
X
3
, y si el eje de rotacin es el eje X
1
, y el plano
de rotacin ser el plano X
2
X
3
(Figura 3.11 a) b) y c) respectivamente).
X
1

X
2

X
3

X
1

X
2

X
3

X
1

X
2

X
3

a) b) c)
72

Figura 3.11: Rotaciones principales 3D: a) eje X
3
, plano X
1
X
2
, b) eje X
2
, plano X
1
X
3
y
c) eje X
1
, plano X
2
X
3
.
Tambin se cumple que las rotaciones 3D dejan fijo un subespacio uni-dimensional,
tal subespacio es el eje de rotacin [Banks 92], lo que significa que todos los puntos que
caen sobre este eje, no se ven afectados por la rotacin. Esto se puede ver grficamente en
la Figura 3.11, donde se observa que en cada una de las rotaciones, los puntos que caen
sobre el eje de rotacin no se ven afectados durante el giro.
Si se renombran las matrices de rotacin 3D, en trminos de planos de rotacin,
colocando como subndices los ejes que forman dicho plano, se tiene:
X
1

X
2


X
3

a)
X
1

X
2

X
3

b)
X
1

X
2

X
3

c)
73

Ecuacin 3.17: Renombramiento de las matrices de rotacin 3D en trminos de planos de rotacin.
3.5.3 Rotaciones 4D
La rotacin en 4D podra resultar en un principio un tanto difcil de comprender,
porque intuitivamente se puede pensar en rotar un objeto alrededor de un eje lineal en el
espacio 4D, porque sta es una idea arraiga en nuestra experiencia en 3D, sin embargo, es
solo una casualidad geomtrica que en el espacio tridimensional el eje de rotacin sea uni-
dimensional.
Tanto [Banks 92] como [Hollasch, 91] coinciden con la idea de que las rotaciones 4D
son similares a las rotaciones 3D, si se piensa en las rotaciones 3D como rotaciones
paralelas a un plano 2D, en lugar de rotaciones alrededor de un eje lineal, como se explica
en la seccin 3.5.2.1 .
A diferencia de la rotacin 3D, donde para hacer rotar un objeto se necesitaba de dos
puntos no coincidentes para formar un eje uni-dimensional de rotacin, en 4D para hacer
rotar un objeto se necesitan tres puntos no colineales que determinan un tringulo, cuyo
plano de soporte define un eje (bi-dimensional) de rotacin.

= =
1 0 0 0
0 cos sin 0
0 sin cos 0
0 0 0 1
) ( ) (
3 , 2 1


R R

= =
1 0 0 0
0 1 0 0
0 0 cos sin
0 0 sin cos
) ( ) (
2 , 1 3


R R

= =
1 0 0 0
0 cos 0 sin
0 0 1 0
0 sin 0 cos
) ( ) (
1 , 3 2


R R
74
X
1

X
2

X
3

X
4

a) b) c)
d) e) f)
X
1

X
2

X
3

X
4

X
1

X
2

X
3

X
4

X
1

X
2

X
3

X
4

X
1

X
2

X
3

X
4

X
1

X
2

X
3

X
4

Tomando en cuenta que en el espacio 4D hay cuatro ejes coordenados: X
1
, X
2
, X
3
y X
4
,
se tienen rotaciones paralelas a los planos formados por todas las posibles combinaciones
de 2 de estos ejes, se obtienen as los seis planos principales 4D: X
1
X
2
, X
1
X
3
, X
1
X
4
, X
2
X
3
,
X
2
X
4
y X
3
X
4
(Figura 3.12).













Figura 3.12: Planos principales 4D: a) plano X
1
X
2
, b) plano X
1
X
3
, c) plano X
1
X
4
, d) plano X
2
X
3
,
e) plano X
2
X
4
y f) plano X
3
X
4
.
[Hollasch 91] se basa en la idea de que solo las dos coordenadas que definen al plano
de rotacin cambiaran dada una rotacin, y construye las seis matrices para las rotaciones
principales 4D.
75

Ecuacin 3.18: Matrices de rotacin 4D.
Se observa que las matrices de rotacin R
1,2
(), R
3,1
() y R
2,3
() son bsicamente las
mismas matrices de la rotacin en 3D (ver Ecuacin 3.17). La expresin de estas matrices
lo que indica es el sentido del giro, por ejemplo la matriz de rotacin R
1,2
(), indica que la
rotacin es del eje X
1
hacia el eje X
2
.
En 3D las rotaciones dejan fijo un subespacio uni-dimensional, tal subespacio es el
eje de rotacin. En 4D las rotaciones dejan fijo un subespacio bi-dimensional, este
subespacio es el eje bi-dimensional de rotacin, y solo se ven afectados los puntos dentro
del plano de rotacin y dentro del conjunto de planos paralelos a l.
Dado que la expresin de la matriz de rotacin indica el plano de rotacin, entonces el
eje bi-dimensional de rotacin est formado por los ejes restantes. Por ejemplo en la Figura

=
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 cos sin
0 0 0 sin cos
) (
2 , 1


R

=
1 0 0 0 0
0 1 0 0 0
0 0 cos 0 sin
0 0 0 1 0
0 0 sin 0 cos
) (
1 , 3


R

=
1 0 0 0 0
0 cos 0 sin 0
0 0 1 0 0
0 sin 0 cos 0
0 0 0 0 1
) (
4 , 2


R

=
1 0 0 0 0
0 1 0 0 0
0 0 cos sin 0
0 0 sin cos 0
0 0 0 0 1
) (
3 , 2


R

=
1 0 0 0 0
0 cos 0 0 sin
0 0 1 0 0
0 0 0 1 0
0 sin 0 0 cos
) (
4 , 1


R

=
1 0 0 0 0
0 cos sin 0 0
0 sin cos 0 0
0 0 0 1 0
0 0 0 0 1
) (
4 , 3

R
76
3.13.a) que representa a la matriz R
1,2
(), el plano de rotacin es el plano X
1
X
2
, el eje bi-
dimensional de rotacin est formado por los ejes coordenados restantes, el plano X
3
X
4
, y se
observa que los puntos que caen sobre este ltimo plano quedan fijos.

Figura 3.13: Rotaciones principales 4D: a) eje X
3
X
4
, plano X
1
X
2
, b) eje X
2
X
4
, plano X
1
X
3
, c) eje X
1
X
4
,
plano X
2
X
3
, d) eje X
2
X
3
, plano X
1
X
4
, e) eje X
1
X
3
, plano X
2
X
4
, f) eje X
1
X
2
, plano X
3
X
4
.
X
1

X
2

X
3

X
4

X
1

X
2

X
3

X
4

X
1

X
2

X
3

X
4

X
1

X
2

X
3

X
4

X
1

X
2

X
3

X
4

X
1

X
2

X
3

X
4

a)
c)
e)
b)
d)
f)
77
3.5.4 Rotaciones nD
Con las ideas anteriores, se puede generalizar el concepto de rotaciones principales en
el espacio nD (n>2), con las siguientes observaciones:
En nD, se necesita proporcionar (n-1) puntos no cohiperplanares cuyo hiperplano de
soporte ser el eje (n-2)-dimensional de rotacin.
En nD las rotaciones dejan fijo un subespacio (n-2)-dimensional, tal subespacio es el
eje (n-2)-dimensional de rotacin, este subespacio est formado por los ejes
coordenados que no pertenecen al plano de rotacin. Y solo se ven afectados los
puntos dentro del plano de rotacin y dentro del conjunto de planos paralelos a l.
En el espacio nD hay n ejes coordenados: X
1
, X
2
, , X
n
, y se tienen rotaciones
paralelas a los planos formados por todas las posibles combinaciones de 2 de estos
ejes, es decir que se tienen ( ) 2 , n C planos principales, esto es precisamente el nmero
de rotaciones principales en el espacio nD.
En [Duffin 94] se seala que especificando el plano de rotacin y el centro de rotacin
de ese plano, la rotacin es nicamente definida, por lo tanto, la rotacin ms simple de
describir en el espacio nD ocurre cuando el plano est formado por cualesquiera dos ejes
coordenados. De esta forma, la matriz de rotacin R
a,b
() para la rotacin de un eje X
a
en la
direccin de un eje X
b
(donde ambos definen el plano de rotacin) por un ngulo , est
dada por la siguiente matriz general de rotaciones principales:

78

Ecuacin 3.19: Matriz general de rotaciones principales nD [Duffin 94].
La Ecuacin 3.19, indica que la matriz R
a,b
() es bsicamente una matriz identidad,
excepto por las intersecciones de las columnas a y b con los renglones a y b, lo que
significa que solo las coordenadas a y b de un punto cambiaran despus de una rotacin
[Aguilera 04].
Para una rotacin en nD, si se utilizan coordenadas homogneas, R
a,b
() es una matriz
de dimensiones (n+1) (n+1), y se puede verificar fcilmente que con n=2, la matriz R
1,2

corresponde a la rotacin positiva alrededor del origen en el espacio 2D (Ecuacin 3.10), y
con n=3, las matrices R
1,2
, R
2,3
y R
3,1
, corresponden a las rotaciones positivas alrededor de
los ejes X
1
, X
2
y X
3
respectivamente en el espacio 3D (Ecuacin 3.17).
Con todos los conceptos generalizados, se puede ver que una rotacin puede ser
expresada usando dos notaciones:
Utilizando los ejes que describen el plano de rotacin. Por ejemplo en 3D, se puede
escribir la rotacin alrededor del eje X
3
como R
1,2
(), y en 4D la rotacin alrededor
del plano X
3
X
4
tambin como R
1,2
().
Utilizando los ejes que describen el eje (n-2)-dimensional de rotacin. En este caso,
en 3D se puede escribir la rotacin alrededor del eje X
3
como R
3
(), y en 4D, la
rotacin alrededor del plano X
3
X
4
como R
3,4
().

=
=
=
=
=
=
=
parte otra en r
b i a i r
r
r
r
r
r R
j i
i i
a b
b a
b b
a a
j i b a
0
, 1
) sin(
) sin(
) cos(
) cos(
) (
,
,
,
,
,
,
, ,

79
Sin embargo, para rotaciones superiores a 4D, puede resultar imprctico utilizar la
segunda notacin, esto se puede observar en la Tabla 2.2, tomada y extendida de [Prez-
guila 01], por tal razn, de aqu en adelante se utiliza slo la primera notacin.
Espacio
nD
Nmero de
rotaciones
principales
Eje (n-2)-dimensional
(subespacio fijo durante la
rotacin)
Ejes principales
que describen el
subespacio fijo
Ejes principales
que describen el
plano de rotacin.
2D

2
2
C = 1 0D Punto X
1
X
2

3D

2
3
C = 3
1D Segmento de recta
(lnea)
X
1

X
2

X
3

X
2
X
3

X
1
X
3

X
1
X
2

4D

2
4
C = 6 2D Plano
X
1
X
2

X
1
X
3

X
1
X
4

X
2
X
3

X
2
X
4

X
3
X
4

X
3
X
4

X
2
X
4

X
2
X
3

X
1
X
4

X
1
X
3

X
1
X
2

5D

2
5
C = 10 3D Volumen
X
1
X
2
X
3

X
1
X
2
X
4
X
1
X
2
X
5
X
1
X
3
X
4
X
1
X
3
X
5
X
1
X
4
X
5
X
2
X
3
X
4

X
2
X
3
X
5
X
2
X
4
X
5
X
3
X
4
X
5
X
4
X
5
X
3
X
5
X
3
X
4
X
2
X
5
X
2
X
4
X
2
X
3
X
1
X
5
X
1
X
4
X
1
X
3
X
1
X
2

nD
2
) 1 (
2

=

n n
n
C (n-2)D Hiperplano (n-2)D
X
1
X
2
X
n-2
X
1
X
2
X
n-3
X
n-1
M
X
2
X
4
X
n
X
3
X
4
X
n
X
n-1
X
n
X
n-2
X
n
M
X
1
X
3
X
1
X
2
Tabla 3.1: Definicin de ejes y planos principales de rotacin para las rotaciones n-dimensionales.
La Figura 3.14, muestra la rotacin R
4,5
() de un hipercubo regular 5D, con los
valores de = 0, 45, 90 y 135, donde se puede observar que todos los puntos del
hipercubo que caen en volumen del eje tridimensional de rotacin formado por los ejes X
1
,
X
2
y X
3
no se ven afectados durante el giro.
80

Figura 3.14: Rotacin R
4,5
() de un hipercubo 5D: a) =0, b) =45, c) =90, d) =135.
3.6 Rotaciones Generales
Se ha presentado y generalizado la matriz de rotacin de rotaciones principales nD,
que se cumple cuando el plano de rotacin y el eje (n-2)-dimensional estn formados por
los ejes coordenados del espacio nD, pero cuando este eje esta definido por puntos
arbitrarios, se necesita de transformaciones adicionales que permitan llevar el eje de
rotacin arbitrario hacia a alguno de los ejes principales del espacio, y de esta forma poder
aplicar las tcnicas para rotaciones principales anteriormente descritas.
X
1

X
2

X
3

X
4

X
5

X
1

X
2

X
3

X
4

X
5

X
1

X
2

X
3

X
4

X
5

X
1

X
2

X
3

X
4

X
5

a) b)
c)
d)
81
3.6.1 Transformaciones Compuestas
Antes de continuar con la generalizacin de las rotaciones, se introduce el tema de
transformaciones compuestas, que es til para obtener el efecto combinado de una serie de
transformaciones geomtricas.
Con la representacin matricial manejada hasta el momento, se puede aplicar una
secuencia de transformaciones, calculando simplemente la multiplicacin matricial de cada
una de las matrices de transformacin. Dado que se est manejando una representacin de
la posicin de un punto p como vector rengln, se puede aplicar una transformacin
compuesta a un punto p, multiplicando las matrices de izquierda a derecha, comenzando
con el punto p.
Por ejemplo, si se desea aplicar una translacin, seguida de un escalamiento a un
punto p, la posicin final del punto p' se calcula de la siguiente manera:
( ) ) ( ) ( ' s S d T p p =
O bien una translacin, seguida de una rotacin:
( ) ) ( ) ( '
,

b a
R d T p p =
En [Hearn 95] se demuestra que las matrices de transformaciones compuestas para el
caso que sean del mismo tipo, se comportan de la siguiente manera:
Las traslaciones sucesivas son aditivas: ) ( ) ( ) (
b a b a
d d T d T d T + =
Los escalamientos sucesivos son multiplicativos: ) ( ) ( ) (
b a b a
s s S s S s S =
Las rotaciones sucesivas son aditivas: ) ( ) ( ) (
, , ,
+ =
b a b a b a
R R R
82
3.6.2 Rotacin General 2D
La rotaciones generales 2D, implican la rotacin de un punto ) , (
2 1
x x p = , dado un
ngulo alrededor de un punto arbitrario (fijo) ) , (
2 1
f f f = (Figura 3.15). Este problema
se resuelve llevndolo a otro ms fcil y conocido, aplicando la tcnica de divide y
vencers, se resuelve en tres etapas.
1. Trasladar el punto f al origen, con una matriz de translacin ) ( f T .
2. Aplicar la rotacin alrededor del origen, con la matriz de rotacin ) ( R .
3. Regresar el punto f a su posicin original, con una matriz de translacin ) ( f T .

Figura 3.15: Rotacin de un punto en 2D alrededor de un punto arbitrario.
De esta forma, la rotacin de un punto p dado un ngulo , alrededor de un punto
arbitrario ) , (
2 1
f f f = en 2D se puede expresar como el producto matricial
) ( ) ( ) ( ' f T R f T p p = , es decir:
[ ] [ ]

=
1
0 1 0
0 0 1
1 0 0
0 cos sin
0 sin cos
1
0 1 0
0 0 1
1 1 ' '
2 1 2 1
2 1 2 1
f f f f
x x x x


Ecuacin 3.20: Expresin matricial para la rotacin general 2D.
f =(f
1
,f
2
)
p=(x
1
,x
2
)
p=(x
1
,x
2
)
X
1

X
2

r
r
83
3.6.3 Rotaciones Generales 3D
Las rotaciones generales 3D, implican la rotacin de un punto p, dado un ngulo
alrededor de un segmento arbitrario ab formado por dos puntos no
coincidentes ) , , (
) 0 (
3
) 0 (
2
) 0 (
1
a a a a = y ) , , (
) 0 (
3
) 0 (
2
) 0 (
1
b b b b = , el problema se resuelve
bsicamente en tres etapas similares al caso 2D.
1. Trasladar el segmento ab de tal forma que quede sobre alguno de los ejes principales
X
1
, X
2
o X
3
, esto se logra mediante una secuencia de combinacin de traslaciones y
rotaciones sobre los ejes principales. Este proceso se analiza ms adelante.
2. Aplicar la rotacin alrededor del eje principal a donde fue llevado el segmento ab , si
se lleva al eje X
1
por ejemplo, se aplica la matriz de rotacin ) (
3 , 2
R .
3. Regresar el segmento ab a su posicin original.
Llevar el segmento ab sobre alguno de los ejes principales, implica otra serie de 3
pasos, los cuales se ilustran en la Figura 3.16.
Se le llamar matriz de IDA a la matriz de transformacin compuesta por una serie de
transformaciones para llevar un segmento ab sobre el eje X
1
(se escoge este eje y no otro, a
manera de visualizar de forma ms sencilla la generalizacin de las rotaciones a
dimensiones superiores). Esta matriz est compuesta de tres transformaciones:
1. En la Figura 3.16 a) se tiene el segmento ab en su posicin original en el espacio 3D,
en la Figura 3.16 b) se traslada este segmento, de tal manera que el punto a queda en
el origen, esto se logra mediante la matriz de translacin ) ( a T .
84
2. Despus en la Figura 3.16 c) se lleva el segmento ab sobre el plano X
1
X
2
, mediante
una rotacin por un ngulo
1
sobre el eje X
1
, esto se logra con la matriz de rotacin
) (
1 2 , 3
R .
3. Finalmente en la Figura 3.16 d) se lleva el segmento ab sobre el eje X
1
, mediante una
rotacin por un ngulo
2
sobre el eje X
3
, esto se logra con la matriz de rotacin
) (
2 1 , 2
R .

Figura 3.16: Proceso en 3D para llevar un segmento arbitrario ab sobre el eje X
1
y regresarlo.
Entonces se tiene que la matriz IDA en 3D esta definida por la ecuacin:
) ( ) ( ) (
2 1 , 2 1 2 , 3
R R a T IDA = , es decir:
2
) 1 (
3
2
) 1 (
2
) 2 (
2
b b b + =
X
1
X
2
a
(3)

b
(3)

X
3
X
1
X
2
X
3
a
(0)

b
(0)

T(-A)
R
3,2
(
1
)
R
2,1
(
2
)
a) b)
c) d)
R
2,1
(-
2
)
R
3,2
(-
1
)
T(A)
Posicin
original
X
3
X
1
X
2
a
(1)

b
(1)

1

1

b
3
(1)

b
2
(1)

b
1
(1)

X
1
X
2
a
(2)

b
(2)

2
X
3
b
1
(2)
=b1
(1)

85

=
1 0 0 0
0 1 0 0
0 0 cos sin
0 0 sin cos
1 0 0 0
0 cos sin 0
0 sin cos 0
0 0 0 1
1
0 1 0 0
0 0 1 0
0 0 0 1
2 2
2 2
1 1
1 1
3 2 1




a a a
IDA
Ecuacin 3.21: Expresin matricial para la matriz IDA 3D.
Se le llamar matriz de REGRESO (utilizando la abreviatura REG de aqu en
adelante) a la matriz de transformacin compuesta por una serie de transformaciones para
llevar de vuelta un segmento ab a su posicin original, como se ve en la Figura 3.16, para
obtener esta matriz se tienen que hacer las transformaciones en un orden inverso al que se
sigue para la matriz IDA, de esta forma, la matriz REG est definida por la siguiente
secuencia de matrices de transformacin: ) ( ) ( ) (
1 2 , 3 1 1 , 2
A T R R REG = .
Una forma ms rpida de obtener la matriz REG, es simplemente obteniendo la matriz
inversa de la matriz IDA, esto es: REG=IDA
-1
. Considerando las siguientes propiedades de
transformaciones [Hearn 95]:
) ( ) (
1
d T d T =

) ( ) ( ) (
, ,
1
,

a b b a b a
R R R = =

Se tiene:
( )
1
2 1 , 2 1 2 , 3
1
) ( ) ( ) (

= = R R a T IDA REG
1 1
1 2 , 3
1
2 1 , 2
) ( ) ( ) (

= a T R R
) ( ) ( ) (
1 2 , 3 2 1 , 2
a T R R =
) ( ) ( ) (
1 3 , 2 2 2 , 1
a T R R =


86
Entonces:

=
1
0 1 0 0
0 0 1 0
0 0 0 1
1 0 0 0
0 cos sin 0
0 sin cos 0
0 0 0 1
1 0 0 0
0 1 0 0
0 0 cos sin
0 0 sin cos
3 2 1
1 1
1 1 2 2
2 2
a a a
REG




Ecuacin 3.22: Expresin matricial para la matriz REG 3D.
Para obtener completamente los valores de las matrices IDA y REG, resta calcular los
ngulos de giro
1
y
2
.
Para obtener el valor del ngulo
1
, observando el tringulo que se forma en la Figura
3.16 b), se tiene que
) 1 (
2
) 1 (
3 1
) tan( b b = , por lo tanto:
) ( 2 arctan
) 1 (
2
) 1 (
3 1
b b = , donde
) 0 (
2
) 0 (
2
) 1 (
2
a b b = y
) 0 (
3
) 0 (
3
) 1 (
3
a b b =
Ecuacin 3.23: Ecuacin para el clculo de
1
.
Para obtener el valor del ngulo
2
, observando el tringulo que se forma en la Figura
3.16 c), se tiene que
) 2 (
1
) 2 (
2 2
) tan( b b = , por lo tanto:
) ( 2 arctan
) 2 (
1
) 2 (
2 2
b b = , donde
) 0 (
1
) 0 (
1
) 1 (
1
) 2 (
1
a b b b = = y
2
) 1 (
3
2
) 1 (
2
) 2 (
2
b b b + =
Ecuacin 3.24: Ecuacin para el clculo de
2
.
Finalmente, la rotacin general 3D de un punto p, dado un ngulo alrededor de un
segmento arbitrario ab se lleva a cabo aplicndole la siguiente secuencia de
transformaciones:
M p p = '
Ecuacin 3.25: Formula para la rotacin general 3D.
REG R IDA M = ) (
3 , 2

Ecuacin 3.26: Matriz de rotacin general 3D.
87
3.6.3.1 Anlisis de las Rotaciones Generales 3D
En [Aguilera04] se presenta un trabajo de generalizacin de las rotaciones
multidimensionales, donde para el caso 3D, el eje de rotacin es de igual forma
representado por la lnea de soporte de un segmento ab (un simplex 1D), donde
( )
) 0 (
3
) 0 (
2
) 0 (
1
, , a a a a = y ( )
) 0 (
3
) 0 (
2
) 0 (
1
, , b b b b = son dos puntos 3D no coincidentes.
Se define a
) 0 (
V , como la matriz que representa los vrtices originales del segmento,
que en coordenadas homogneas esto es:

=
1
1
) 0 (
3
) 0 (
2
) 0 (
1
) 0 (
3
) 0 (
2
) 0 (
1 ) 0 (
b b b
a a a
V
y
k
M como la matriz correspondiente a la k-sima transformacin. Entonces se tiene el
conjunto { } K , , ,
) 2 ( ) 1 ( ) 0 (
V V V , donde
k
k k
M V V =
1
. Este conjunto es la serie de matrices
que contienen las coordenadas modificadas de los vrtices despus de cada transformacin,
es decir:

=
1
1
) (
3
) (
2
) (
1
) (
3
) (
2
) (
1 ) (
k k k
k k k
k
b b b
a a a
V o simplemente

=
) (
) (
) (
k
k
k
b
a
V
Entonces segn lo analizado en la seccin 3.6.3 , para llevar a cabo una rotacin 3D
alrededor de un segmento arbitrario, se tiene que
1
M es ) (
) 0 (
a T y de esta forma:

= =
1
0 1 0 0
0 0 1 0
0 0 0 1
1
1
) ( ) (
) 0 (
3
) 0 (
2
) 0 (
1
) 0 (
3
) 0 (
2
) 0 (
1
) 0 (
31
) 0 (
2
) 0 (
1 ) 0 (
) 0 (
) 0 (
) 0 ( ) 0 ( ) 1 (
a a a
b b b
a a a
a T
b
a
a T V V

=
1
1 0 0 0
) 0 (
3
) 0 (
3
) 0 (
2
) 0 (
2
) 0 (
1
) 0 (
1
a b a b a b

88
Lo importante de observar en este paso, es que las coordenadas del punto a se van al
origen, es decir valen cero.
Siguiendo el proceso, se tiene que
2
M es la matriz de rotacin ) (
1 2 , 3
R , por lo tanto:

=
1 0 0 0
0 cos sin 0
0 sin cos 0
0 0 0 1
1
1 0 0 0
) (
1 1
1 1
) 1 (
3
) 1 (
2
) 1 (
1
1 2 , 3
) 1 (
) 1 (
) 2 (

b b b
R
b
a
V

+ +
=
1 cos sin sin cos
1 0 0 0
1
) 1 (
3 1
) 1 (
2 1
) 1 (
3 1
) 1 (
2
) 1 (
1
b b b b b

Teorema:
Al aplicar la matriz ) (
1 2 , 3
R , se est usando el plano de rotacin X
2
X
3
, y el ngulo de
rotacin necesario para llevar el segmento hacia el plano X
1
X
2
, de tal forma que la
coordenada
) 2 (
3
b se vaya a cero, est dado por ( )
) 1 (
2
) 1 (
3 1
2 arctan b b = .
Demostracin:
Tomando en cuenta las siguientes identidades trigonomtricas:
2
1
)) ( 2 sin(arctan
x
x
x
+
=
2
1
1
)) ( 2 cos(arctan
x
x
+
= ,
se calculan los valores de
) 2 (
2
b y
) 2 (
3
b .
1
) 1 (
2 1
) 1 (
2
) 2 (
2
sin cos b b b + =
( ) ( ) ( ) ( )
) 1 (
2
) 1 (
3
) 1 (
3
) 1 (
2
) 1 (
2
) 1 (
2
2 arctan sin 2 arctan cos b b b b b b + =

( ) ( )
( )
( )

+
+
=

+
+

+
=
2
) 1 (
2
) 1 (
3
) 1 (
2
2
) 1 (
3
) 1 (
2
2
) 1 (
2
) 1 (
3
) 1 (
2
) 1 (
3
) 1 (
3
2
) 1 (
2
) 1 (
3
) 1 (
2
1 1 1
1
b b
b b b
b b
b b
b
b b
b
89

( ) ( )
( ) ( )
) 1 (
2
2
) 1 (
3
2
) 1 (
2
) 1 (
2
2
) 1 (
3
2
) 1 (
2
b
b b
b
b b
+
+
=

( ) ( )
( ) ( )
2
) 1 (
3
2
) 1 (
2
2
) 1 (
3
2
) 1 (
2
b b
b b
+
+
=
( ) ( )
2
) 1 (
3
2
) 1 (
2
b b + =
1
) 1 (
3 1
) 1 (
2
) 2 (
3
cos sin b b b + =
( ) ( ) ( ) ( )
) 1 (
2
) 1 (
3
) 1 (
3
) 1 (
2
) 1 (
3
) 1 (
2
2 arctan cos 2 arctan sin b b b b b b + =

( ) ( )

+
+

+
=
2
) 1 (
2
) 1 (
3
3
2
) 1 (
2
) 1 (
3
) 1 (
2
) 1 (
3 ) 1 (
2
1
1
1 b b
b
b b
b b
b

( )

+
+
=
2
) 1 (
2
) 1 (
3
) 1 (
3
) 1 (
3
1 b b
b b

0 =
Por lo tanto
( ) ( )

+
=
1 0
1 0 0 0
2
) 1 (
3
2
) 1 (
2
) 1 (
1
) 2 (
b b b
V
Enseguida, se tiene que
3
M es la matriz de rotacin ) (
2 1 , 2
R , por lo tanto:

=
1 0 0 0
0 1 0 0
0 0 cos sin
0 0 sin cos
1 0
1 0 0 0
) (
2 2
2 2
) 2 (
2
) 2 (
1
2 1 , 2
) 2 (
) 2 (
) 3 (

b b
R
b
a
V

+ +
=
1 0 cos sin sin cos
1 0 0 0
2
) 2 (
2 2
) 2 (
1 2
) 2 (
2 2
) 2 (
1
b b b b

90
Teorema:
Al aplicar la matriz ) (
1 1 , 2
R , se est usando el plano de rotacin X
1
X
2
, y el ngulo de
rotacin necesario para llevar el segmento hacia el eje X
1
, de tal forma que la coordenada
) 3 (
2
b se vaya a cero, est dado por ( )
) 2 (
1
) 2 (
2 2
2 arctan b b = .
Demostracin:
Este proceso se puede demostrar de la misma forma que la hiptesis anterior, y se ve
claramente que se llega a los siguientes resultados:
( ) ( )
2
) 2 (
2
2
) 2 (
1
) 3 (
1
b b b + =
0
) 3 (
2
= b
Por lo tanto
( ) ( ) ( )

+ +
=
1 0 0
1 0 0 0
2
) 1 (
3
2
) 1 (
2
2
) 1 (
1
) 3 (
b b b
V
La aplicacin de las matrices
2
M y
3
M muestran que si se desea hacer igual a cero la
j-sima coordenada, se aplica una rotacin dada por la siguiente ecuacin:
( ) ( )
) 1 (
1
) 1 (
1 ,
, 2 arctan

=
k
j
k
j j j k
b b R M
Ecuacin 3.27: Matriz de rotacin para llevar la j-sima coordenada a cero [Aguilera 04].
Hasta este punto, se tiene al segmento ab sobre el eje X
1
, es decir que la matriz
3 2 1
M M M IDA = , por lo tanto el siguiente paso es aplicar la rotacin sobre el eje X
1
con
el ngulo deseado, por lo tanto
4
M es la matriz de rotacin ) (
3 , 2
R . El proceso final es
regresar el eje de rotacin a su posicin original, aplicando las matrices M
5
, M
6
y M
7
que
son las matrices inversas de M
3
, M
2
y M
1
respectivamente, entonces, se tiene que la matriz
REG est definida como:
1 1
1
1
2
1
3 7 6 5

= = = IDA M M M M M M REG .
91
De esta forma, para llevar a cabo la rotacin general 3D de un punto p, dado un
ngulo alrededor de un segmento arbitrario ab se aplican la Ecuacin 3.25 y la Ecuacin
3.26.
3.6.4 Rotaciones Generales 4D
Las rotaciones generales 4D, implican la rotacin de un punto p, dado un ngulo
alrededor de un plano, definido por el plano de soporte de un tringulo (abc) (un simplex
2D), donde ( )
) 0 (
4
) 0 (
3
) 0 (
2
) 0 (
1
, , , a a a a a = , ( )
) 0 (
4
) 0 (
3
) 0 (
2
) 0 (
1
, , , b b b b b = , y ( )
) 0 (
4
) 0 (
3
) 0 (
2
) 0 (
1
, , , c c c c c = son
tres puntos no colineales. El problema se resuelve nuevamente en tres etapas similares al
caso 3D.
1. Trasladar el tringulo (abc) de tal forma que quede completamente sobre el plano
principal X
1
X
2
, y que el eje ab quede alineado sobre el eje X
1
.
2. Aplicar la rotacin alrededor del plano principal X
1
X
2
, mediante la matriz de rotacin
) (
4 , 3
R .
3. Regresar el tringulo (abc) a su posicin original.
Llevar el tringulo (abc) al plano X
1
X
2
y que el eje ab quede alineado sobre X
1
,
implica una serie de 6 pasos, los cuales se ilustran en la Figura 3.17.
Se define el conjunto { } K , , ,
) 2 ( ) 1 ( ) 0 (
V V V como la serie de matrices que contienen las
coordenadas modificadas de los vrtices del tringulo despus de cada transformacin,
donde
k
k k
M V V =
1
, y
) 0 (
V es la matriz que define los vrtices originales del tringulo.

=
1
1
1
) 0 (
4
) 0 (
3
) 0 (
2
) 0 (
1
) 0 (
4
) 0 (
3
) 0 (
2
) 0 (
1
) 0 (
4
) 0 (
3
) 0 (
2
) 0 (
1
) 0 (
c c c c
b b b b
a a a a
V
92
1. En la Figura 3.17 a) se tiene el tringulo (abc) en su posicin original en algn lugar
del espacio 4D. En la Figura 3.17 b) se traslada este tringulo, de tal manera que el
punto a queda en el origen. Se tiene entonces que ( )
) 0 (
1
a T M = y por lo tanto:

= =
1
1
1 0 0 0 0
) (
) 1 (
4
) 1 (
3
) 1 (
2
) 1 (
1
) 1 (
4
) 1 (
3
) 1 (
2
) 1 (
1
) 0 ( ) 0 ( ) 1 (
c c c c
b b b b a T V V
2. En la Figura 3.17 c) se lleva el segmento ab del tringulo dentro del volumen
X
1
X
2
X
3
. Aplicando la Ecuacin 3.27, la cual realiza una rotacin de la j-sima hacia la
(j-1)-sima dimensin, haciendo que la j-sima coordenada se haga cero, se tiene que
( ) ( )
) 1 (
3
) 1 (
4 3 , 4 1 3 , 4 2
2 arctan ) ( b b R R M = = y por lo tanto:

= =
1
1 0
1 0 0 0 0
) (
) 2 (
4
) 2 (
3
) 2 (
2
) 2 (
1
) 2 (
3
) 2 (
2
) 2 (
1 1 3 , 4
) 1 ( ) 2 (
c c c c
b b b R V V
3. En la Figura 3.17 d) se lleva el segmento ab sobre el plano X
1
X
2
. Aplicando de nuevo
la Ecuacin 3.27, se tiene que ( ) ( )
) 2 (
2
) 2 (
3 2 , 3 2 2 , 3 3
2 arctan ) ( b b R R M = = y por lo tanto:

= =
1
1 0 0
1 0 0 0 0
) (
) 3 (
4
) 3 (
3
) 3 (
2
) 3 (
1
) 3 (
2
) 3 (
1 2 2 , 3
) 2 ( ) 3 (
c c c c
b b R V V
4. En la Figura 3.17 e) se lleva el segmento ab sobre el eje X
1
. Aplicando la Ecuacin
3.27, se tiene que ( ) ( )
) 3 (
1
) 3 (
2 1 , 2 3 1 , 2 4
2 arctan ) ( b b R R M = = y por lo tanto:

= =
1
1 0 0 0
1 0 0 0 0
) (
) 4 (
4
) 4 (
3
) 4 (
2
) 4 (
1
) 4 (
1 3 1 , 2
) 3 ( ) 4 (
c c c c
b R V V
93

Figura 3.17: Proceso en 4D para llevar un tringulo (abc) arbitrario sobre el plano X
1
X
2
y regresarlo.
T(-A)
T(A)
R
3,2
(
2
)

R
3,2
(-
2
)

R
4,3
(
1
) R
4,3
(-
1
)
R
2,1
(-
3
) R
2,1
(
3
)
R
4,3
(
4
)

R
4,3
(-
4
)
b
(0)

X
1

X
2

X
3

X
4

a
(0)

c
(0)

a)
X
1

X
2

X
3


b
4
(1)

a
(1)

b
(1)

c
(1)

b
3
(1)

1

b)
X
1

X
2

X
3

X
4


a
(2)

b
(2)

b
3
(2)

b
2
(2)

2

c)
c
(2)

X
1

X
2

X
3

X
4

3

b
2
(3)

b
1
(3)

a
(3)

b
(3)

c
(3)

d)
X
1

X
2

X
3

X
4

b
(4)
a
(4)

c
(4)

4

c
4
(4)

c
3
(4)

e)
X
1

X
2

X
3

X
4

R
3,2
(
5
) R
3,2
(-
5
)
f)
c
2
(5)

c
3
(5)

b
(5)

a
(5)

c
(5)

5

X
1

X
2

X
3

X
4

a
(6)

b
(6)

c
(6)

g)
94
Hasta este momento se puede observar que el segmento modificado
) 4 ( ) 4 (
b a se
encuentra sobre el eje X
1
, sin embargo el punto
) 4 (
c , que tambin sufri
modificaciones, se encuentra en alguna parte del espacio 4D. Ahora es necesario
mover este punto de tal forma que el tringulo se encuentre completamente sobre el
plano X
1
X
2
, para ello, se tiene que trabajar con el segmento ac y aplicar rotaciones
que no involucren al eje X
1
, para no modificar la posicin del segmento ab , ya que
como se especifica en las observaciones de la Seccin 3.5.4 , una rotacin ) (
,

b a
R ,
modifica las coordenadas dentro del plano de rotacin formado por los ejes X
a
y X
b
, y
dejan fijo todos los puntos que no pertenecen a este. Entonces se prosigue de la
siguiente forma:
5. En la Figura 3.17 f) se lleva el segmento ac dentro del volumen X
1
X
2
X
3
. Aplicando la
Ecuacin 3.27, se tiene que ( ) ( )
) 4 (
3
) 4 (
4 3 , 4 4 3 , 4 5
2 arctan ) ( c c R R M = = y por lo tanto:

= =
1 0
1 0 0 0
1 0 0 0 0
) (
) 5 (
3
) 5 (
2
) 5 (
1
) 5 (
1 4 3 , 4
) 4 ( ) 5 (
c c c
b R V V
6. En la Figura 3.17 g) se lleva el segmento ac sobre el plano X
1
X
2
. Aplicando la
Ecuacin 3.27, se tiene que ( ) ( )
) 5 (
2
) 5 (
3 2 , 3 5 2 , 3 6
2 arctan ) ( c c R R M = = y por lo tanto:

= =
1 0 0
1 0 0 0
1 0 0 0 0
) (
) 6 (
2
) 6 (
1
) 6 (
1 5 2 , 3
) 5 ( ) 6 (
c c
b R V V
Con esto, se tiene el tringulo (abc) completamente sobre el plano X
1
X
2
, el
siguiente paso es aplicar la rotacin sobre este plano con el ngulo deseado, por lo tanto
95
) (
4 , 3 7
R M = . El proceso final es regresar el tringulo a su posicin original, aplicando las
matrices de M
8
a M
13
que son las matrices inversas de M
6
a M
1
respectivamente.
Entonces se definen a las matrices IDA y REG 4D como:

=
=
6
1 k
k
M IDA
1
13
8

=
= =

IDA M REG
k
k

De esta forma, la rotacin general 4D de un punto p, dado un ngulo alrededor de
un plano arbitrario est definida como:
M p p = '
Ecuacin 3.28: Formula para la rotacin general 4D.
REG R IDA M = ) (
4 , 3

Ecuacin 3.29: Matriz de rotacin general 4D.
3.6.5 Rotaciones Generales nD
Las rotaciones generales nD, implican la rotacin de un punto p, dado un ngulo
alrededor de un hiperplano (n-2)-dimensional arbitrario definido por n-1 puntos no
cohiperplanares, que representan un simplex (n-2)D.
En general, el problema se resuelve en tres etapas similares a los casos 3D y 4D.
1. Trasladar el hiperplano (n-2)-dimensional de tal forma que quede completamente
dentro del hiperplano principal X
1
X
2
...X
n-2
.
2. Aplicar la rotacin alrededor del hiperplano principal X
1
X
2
...X
n-2
, mediante la matriz
de rotacin ) (
, 1

n n
R

.
3. Regresar el hiperplano (n-2)-dimensional a su posicin original.
96
Llevar el hiperplano (n-2)-dimensional de rotacin completamente sobre el hiperplano
X
1
X
2
...X
n-2
implica una serie de pasos que se explican a continuacin.
Se define el conjunto { } K , , ,
) 2 ( ) 1 ( ) 0 (
V V V como la serie de matrices que contienen los
vrtices modificados de los vrtices del hiperplano (n-2)-dimensional despus de cada
transformacin, donde
k
k k
M V V =
1
y
) 0 (
V es la matriz que define las coordenadas
originales. En general la matriz
) (k
V para la rotacin en nD se define como:

=

1
1
1
) (
, 1
) (
3 , 1
) (
2 , 1
) (
1 , 1
) (
, 2
) (
3 , 2
) (
2 , 2
) (
1 , 2
) (
, 1
) (
3 , 1
) (
2 , 1
) (
1 , 1
) (
k
n n
k
n
k
n
k
n
k
n
k k k
k
n
k k k
k
v v v v
v v v v
v v v v
V
L
M M O M M M
L
L
o bien,

) (
1
) (
2
) (
1
) (
k
n
k
k
k
V
V
V
V
M

El primer paso en cualquier dimensin es trasladar las coordenadas del punto
) 0 (
1
V al
origen, entonces se tiene que ( )
) 0 (
1 1
V T M = y por lo tanto:

= =

1
1
1 0 0 0
) (
) 1 (
, 1
) 1 (
3 , 1
) 1 (
2 , 1
) 1 (
1 , 1
) 1 (
, 2
) 1 (
3 , 2
) 1 (
2 , 2
) 1 (
1 , 2 ) 0 (
1
) 0 ( ) 1 (
n n n n n
n
v v v v
v v v v
V T V V
L
M M O M M M
L
L

De aqu, se generaliza el proceso partiendo de los resultados obtenidos en 3D y 4D.
La idea es llevar el segmento
2 1
V V sobre el eje principal X
1
mediante rotaciones principales
similares a los casos 3D y 4D; despus llevar el segmento
3 1
V V sobre el plano principal
X
1
X
2
, utilizando rotaciones principales que no involucren al eje X
1
para no alterar la
posicin de los vrtices V
1
y V
2
ya

posicionados sobre este eje; enseguida llevar el segmento
4 1
V V dentro del volumen principal X
1
X
2
X
3
, utilizando rotaciones principales que no
involucren las coordenadas que forman al plano X
1
X
2
para no alterar la posicin de los
vrtices V
1
, V
2
y V
3
ya posicionados sobre este plano; y as sucesivamente hasta llevar el
97
segmento
n
V V
1
dentro del hiperplano principal X
1
X
2
X
n-2
, utilizando rotaciones principales
que no involucren a los ejes que forman al hiperplano X
1
X
1
X
n-3
para no alterar la posicin
de los vrtices V
1
, V
2
, , V
n-2
ya posicionados dentro de este hiperplano.
Entonces la matriz general IDA formada por el conjunto de matrices de
transformacin requeridas para llevar el hiperplano (n-2)-dimensional de tal forma que
quede completamente sobre el hiperplano principal X
1
X
2
X
n-2
, debe de convertir la matriz
) 0 (
V a una
) (k
V de la siguiente manera:

1 0 0
1 0 0 0
1 0 0 0 0
1
1
1
) (
2 , 1
) (
1 , 1
) (
1 , 2
) 0 (
, 1
) 0 (
3 , 1
) 0 (
2 , 1
) 0 (
1 , 1
) 0 (
, 2
) 0 (
3 , 2
) 0 (
2 , 2
) 0 (
1 , 2
) 0 (
, 1
) 0 (
3 , 1
) 0 (
2 , 1
) 0 (
1 , 1
k
n n
k
n
k
n n n n n
n
n
v v
v
IDA
v v v v
v v v v
v v v v
L
M M M O O M
L
L
L
M M O M M M
L
L

Despus de este proceso lo que se tiene es que el vrtice
) (
1
k
V se encuentra en el
origen, el vrtice
) (
2
k
V sobre el eje X
1
, el vrtice
) (
3
k
V sobre el plano X
1
X
2
, y as
sucesivamente, teniendo finalmente el vrtice
) (
1
k
n
V

dentro del hiperplano X
1
X
2
...X
n-2
.
Procediendo de forma similar a los casos 3D y 4D, lo que se necesita para lograr esa
matriz es hacer cero una columna c y rengln r dado, por lo que se hace uso de la Ecuacin
3.27, la cual se puede reescribir como:
( ) ( )
) 1 (
1 ,
) 1 (
, 1 ,
, 2 arctan

=
k
c r
k
c r c c k
V V R M
De esta forma, se tiene que en el primer rengln se necesita hacer cero n coordenadas,
en el segundo n-1, en el tercero n-2, y as sucesivamente hasta que en el (n-1)-simo
rengln se necesitan hacer cero solamente dos coordenadas, lo que indica claramente que el
nmero de rotaciones que hay que llevar a cabo ser equivalente a la suma de los (n-1)
primeros enteros positivos, (n-1) porque los n ceros del primer rengln se obtienen de la
98
translacin de ( )
) 0 (
1
V T y se resta 1 porque se comienza desde hacer cero 2 coordenadas,
por lo tanto:
1
2
) 1 (
1
2
) 1 1 )( 1 (

=
+ n n n n

Se necesitan entonces, 1 2 ) 1 ( n n matrices de rotacin para que el hiperplano (n-
2)-dimensional quede completamente sobre el hiperplano principal X
1
X
2
X
n-2
. Dado que
las rotaciones comienzan en k=2, se tiene que las matrices generales IDA y REG estn
dadas por:

Ecuacin 3.30: Matrices generales IDA y REG nD.
Se puede concluir que las rotaciones generales multidimensionales de un punto p,
dado un ngulo alrededor de un hiperplano (n-2)-dimensional arbitrario estn dadas por
las siguiente ecuaciones:
M p p = '
Ecuacin 3.31: Formula para la rotacin general nD.
REG R IDA M
n n
=

) (
, 1

Ecuacin 3.32: Matriz de rotacin general nD.
A continuacin se presenta el algoritmo Aguilera-Perez propuesto en [Aguilera04], en
el cul se puede apreciar claramente el clculo de cada una de las matrices de
transformacin, necesarias para generar la matriz de rotacin general nD.

=
=
2
) 1 (
2
1
n n
k
k
M M IDA
1
= IDA REG
99
Procedure ComputeM(
) 0 (
V ,,n)
M
1
:=T(-V
1
(0)
)
V
(1)
:=V
(0)
M
1

M:=M
1

k:=1
for r:=2 to n-1 do
for c:=n downto r do
k:=k+1;
M
k
=R
c,c-1
(arctan2(V
r,c
(k-1)
,V
r,c-1
(k-1)
))
V
(k)
:=V
(k-1)
M
k

M:=MM
k

endfor
endfor
M:=MR
n,n-1
()
M:=MM
-1

endprocedure
3.7 Resumen
En este captulo se analizaron algunas transformaciones geomtricas n-dimensionales,
donde se pudo ver que las transformaciones de escalamiento, y translacin son fcilmente
llevadas a su forma general para cualquier espacio nD.
Dentro de las rotaciones, se analizaron en primer lugar las rotaciones principales, que
se llevan a cabo alrededor de los ejes principales que forman el espacio nD, presentando la
matriz general para tales rotaciones. Enseguida se present el mtodo para poder llevar a
cabo las rotaciones alrededor de cualquier eje (n-2)-dimensional de rotacin arbitrario,
utilizando una combinacin de transformaciones de translacin y rotaciones principales,
definiendo de esta forma, las matrices generales IDA y REG, para finalmente obtener la
matriz para rotaciones generales.
El mtodo para rotaciones generales presentado en este captulo es aplicable cuando
se cuenta con n-1 puntos no cohiperplanares, que representan un simplex (n-2)D. En el
siguiente captulo se desarrolla un mtodo para rotaciones generales, mediante operaciones
vectoriales, aplicable cuando se proporciona el plano de rotacin.