[Solutions to paper 1]

1
Solution:
3 2
1 7 10
0
x x x
+ + 0 x

2
3
1 7 10
0
x x
x
+ +


3
(1 5 )(1 2 )
0
x x
x
+ +

(1 5 )(1 2 ) 0 x x x + + since
2
0 x >



0 x > or
1 1
2 5
x
For
2
3 2
1 7 10
0 x
x x x
| |
+ + <
|
\ .
0 x

3 2
1 7 10
0
x x x
+ + < as
2
0 x >
Since
3 2
1 7 10 1 1
0 0 or
2 5
x x
x x x
+ + >
2
3 2
1 7 10
0 x
x x x
| |
+ + <
|
\ .

1
2
x < or
1
0
5
x < <

2
2 1
1 tan 2 x y x

+ =
Differentiate with respect to x,
( )
2
2
1 2
1 2
dy
y
dx
x
+ =
+

Differentiate with respect to x again,
1/2 1/5 0
( )
( )
2
2
2 2
2
16
2 2
1 2
dy d y x
y
dx dx
x
| | | |
+ =
| |
\ .
\ .
+

Let 0 x = , ( ) 1 0 y y = > ,
1
2
dy
dx
= ,
2
2
1
4
d y
dx
=
2 2
1 1 1 1 1
1 ... 1
2 2 4 2 8
y x x x x
| |
= + + +
|
\ .


3
( )
| |
sin ln cos d
sin
cos ln(cos ) cos d
cos
cos ln(cos ) sin d
cos ln(cos ) cos
cos 1 ln(cos )
x x x
x
x x x x
x
x x x x
x x x c
x x c
| |
= +
|
\ .
=
= + +
= +

( )
( ) ( )
( ) ( )
( )
4
4
0
4
0
4
sin ln cos d
sin ln cos d sin ln cos d
1 1
1 ln 2 1 1 ln 2 1
2 2
2 1 ln 2 2
x x x
x x x x x x

= +
= + + +
= +

4
To prove the statement that
1
5 1 1
3 4 3
n
n
u

| |
= +
|
\ .
for all , 1 n n
+
.

Let 1 n =

LHS:
1
2 u = (Given)
RHS:
5 1
(1) 2
3 3
+ =

The statement is true for the case of 1 n =
Assume that the statement is true for some , 1 k k
+

To prove statement is true for
1
5 1 1
1 i.e.
3 4 3
k
k
k u
+
| |
+ = +
|
\ .

( )
1
1
1
1
4
1 5 1 1
1
4 3 4 3
5 1 1
3 4 3
k k
k
k
u u
+

= +
(
| |
= + +
(
|
\ .
(

| |
= +
|
\ .

If the statement is true for n k = , it is also true for 1 n k = + . Since the statement is true for 1 n = , the
statement is true for all n
+
.

1
5 1 1
3 4 3
n
n
u

| |
= +
|
\ .
,
As n ,
1
1
0
4
n
| |

|
\ .
.
1
3
n
u . Sequence converges.
Note that as n increases,
1
1
4
n
| |
|
\ .
decreases and therefore
n
u decreases.

Therefore the maximum value of
n
u occurs at
1
2 u = .
The range of ,
n
u
1
2
3
n
u <

5
2
3 ( 2)( 2) ( 1) r r r r r = + 1 a =
(i)
( ) ( )
( ) ( )
2
1 1
1
3 ( 2)( 2) ( 1)
ln ln
2 ! 2 2 ! 2
2 1
ln( ) ln( 2)
1 ! 2 !
1
0 0 ln3
2!
1
0 ln2 ln4
4!
1 2
ln3 ln5
4! 5!
.
.
.
3 2
ln( 1) ln(
( )! ( 1)!
N N
r r
N
r
r r r r r r r
r r r r
r r
r r
r r
N N
N N
N N
= =
=
( (
+ | | | |
+ = +
( ( | |
+ + + +
\ . \ .

(

= + +
(
+ +

= +
+ +
+ +
+
+
+

+ +
+

( )
1)
2 1
ln( ) ln( 2)
( 1)! ( 2)!
1 1 2
ln
2 2 ! ( 1)( 2)
N N
N N
N N
N
N N N
+

+ + +
+ +
(
= +
(
+ + +



(ii) No, the series does not converge. As
2
, ln
( 1)( 2)
N
N N
(

(
+ +

, therefore the sequence
diverges.

6
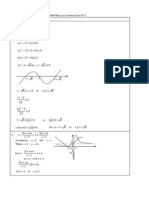
Graph of
4
2
x
y
x

(i) { :2 4} A x x = <
Let
4
2
x
y
x

for 2 4 x <
2 4 y xy x =
2 4 x xy y + = +

2 4
1
y
x
y
+
=
+
Hence
1
2( 2)
:
1
x
f x
x

+
+
, 0 x
(ii) For 2 4 x < ,
4 4
f ( )
2 2
x x
x
x x

= =

.
Let
4
f ( )
2
x
u x
x

= =

.
2 4 u ux x =

2 4
1
u
x
u
+
=
+

Now
2
4(3 )
gf ( )
(2 )
x
x
x

2
2 4
4 3
1
g( )
2 4
2
1
u
u
u
u
u
+ | |

|
+
\ .
=
+ | |

|
+
\ .


2
3 3 2 4
4
1
g( )
2 2 2 4
1
u u
u
u
u u
u
+ | |
|
+
\ .
=
+ | |
|
+
\ .


2
4 4 ( 1)
g( )
1 4
u u
u
u
+
=
+


2
g( ) ( 1)( 1) 1 u u u u = + =

2
g( ) 1 x x =
7
(i)
2
1 1
, 0,
2( 1) 2 2 2( 1)
x a x a
y a a
x x
+
= = + +


2
2 2
2 1 1
2( 1) 2 2( 1)
dy x x a a
or
dx x x
+
=


2
0 ( 1) 1 1
dy
x a x a x a
dx
= = = =
C has two stationary points 0
dy
dx
= has two distinct real roots 0 a >
2
2
0 has 2 distinct roots
2 1 0 has two distinct roots
(-2) 4(1 ) 0 0
dy
Or
dx
x x a
a a
=
+ =
> >

(ii) C has no stationary points i.e. a <0
1
2 2 2( 1)
x a
y
x
= + +

The asymptotes are
1
2 2
x
y = + and 1 x =


(iii) From the diagram, the graph of
2
1
2( 1)
x a
y
x
+
=

and 1 1 y k x = + intersect
at two points when
1 1
2 2
k < <
For
2
2 4
1
2
x x
k x
x
+
= + to have two real roots ,
1 1
2 2
k < <
8
(i)
2 2
d 1 d
,
d d
1 1
y x

= =


2
2
d d d 1 1 1
d d d
1
y y
x x

| |

= = = |
|

\ .

d
1
d
y
x
=
1 =
Coordinates of P is 0,
2
| |
|
\ .

(ii)
d d
1
dt d
y
x
| |
=
|
\ .


d d d
1
d d dt
y
x

| | (
=
|
(
\ .


d d d d
1
d d d d
y y
x y t

(
| | (
=
| (
(
\ .



| |
2
2
2
2 2
d 1
1 2 1
d
2
1 1
2 1 0 0.910

| |
(
=
|

\ .
=
= =

1 x =

( )
1
1
2
y x = +

( 1 ,0) a

( 1 ,0) a

1
0,
2
a | |
|
\ .

9
(a) i)
( )
( )
( )
2 2
2
2
4
2 2
0 0 2 2
4 4tan .2sec
4
d
4 4 4tan
x
x d
x

=
+ +



2 2
4
4
0
2
4
2
0
tan .sec
2
sec
tan
2
sec
d
d

=
=

2
4
0
2 sin d

=


( )
4
0
1 cos2 d

4
0
1
sin2
2

(
=
(


=
1
sin
4 2 2

=
1
(proved)
4 2

Area =
( )
2
2
2
0 2
4 2 1
1 d
2 1
4
x x
x
x
x
| |
| |
|
+
|
| +
\ .
+
\ .

( )
2
2
2
0 2
4 2
1 1 d
2 1
4
x
x
x
x
| |
| |
|
= +
|
| +
\ .
+
\ .

( )
2
2 2
2
0 0 2
4 2
d
2 1
4
x
dx x
x
x
= +
+
+



2
0
1 2
+ ln 2 1
4 2 2
x

= + (



1
+ln5
4 2

=





(b)













( )
2
4 1
1 4
y x
x y
=
=


Point A = (2, 3) from GC
Volume = ( )
( )
4
2 2 2
1 2
3
1
2 3
3
x x dy +

( ) ( )
2 2 4
3
4 1 4 1 4 y y dy = + +

= 20.9 (correct to 3 significant figures)

10 (i)










(ii)









y
x
0
1 -2
y =1/f(x)
y = 0.5 A(0,)
x =-2
y


A(2,2)
B(6,0) 0
y = 2
y = f (1-x)
x = 0
(iii)










For the curve g( ) y x = to have 2 stationary pts, 2 0 a < < , the nature of stationary
point C is a maximum point and the nature of stationary point D is a minimum point.

11 Scheme A: AP with first term 10 a = and common difference 0.25 d = .
Scheme B: GP with first term 10 a = and common ratio 1.025 r = .

(i) On 17 July, it will be the 17
th
day for Albert and the 8
th
day for James.
Daily distance complete by Albert = 10 (17 1)(0.25) + = 14
Daily distance complete by James =
8 1
10(1.025)

= 11.88686
Difference = 14 11.88686 = 2.11 km (3 sig. fig.)
(ii) Let n be the number of days taken by James for his daily distance to exceed Albert.
The number of days taken by Albert will be n + 9.

1
10(1.025) 10 ( 9 1)(0.25)
n
n

> + +

1
10(1.025) 10 ( 8)(0.25) 0
n
n

+ >

From GC, 25.809 n >
When n = 26, the date is 4 August.
(iii) Albert will complete his training when
| | 2(10) ( 1)(0.25) 500
2
n
n + >
Least n = 36 from GC
Albert will take 36 days to complete his training.
(iv) James will complete his training when
10(1.025 1)
500
1.025 1
m

>

Least m = 33 from GC
Hence number of more days taken = 33 + 9 36 = 6 more days
y


A(0,
3
)
B(-2,1)
0
3 y =
y = f(x)+1
3 y =

1 x =
1 y =
1 y =
12 (a)
2
1
8
8
8
dx k
x
dt x
x k
x
=
+
=

2
2
4 1
8
x
dx dt
x k
=
+


2
4ln 8 x k t c + = + , where c is an arbitrary constant.
2
4
8
t c
x k e
+
+ =
1
2
4
8
t
x k Ae

+ = , where k and A are constants.

(ii) Given that 0 t = , 3 x = and 1 t = , 2 x =
9 8k A + =

1
4
4 8k Ae

+ =
Using GC, 22.60406 A =

To find the time required to remove all the mines, i.e. 0 x =
8
4ln
9
4ln
2.03
k
t
A
A
t
A
t
=

=
=

Therefore, it will take 2.03 months to clear all the mines.

(b) 2 d y dy x x = +


2 2
2
2 2
y x
x c = + + , where c is an arbitrary constant.
2 2
4 2 y x x c = + +
( ) ( )
2 2
2
2 4 2 2 y x c x A = + + = + + , where 2 4 A c =


A > 0
A < 0
A=0
13
(i) Vector between the 2 fixed pts =
1 0
0 1
1 1
| | | |
| |

| |
| |
\ . \ .
=
1
1
0
| |
|
|
|
\ .

Distance between the 2 // lines = Distance of a pt on l
1
to l
2
.
Distance of pt (1,0,1) to the line l
2
=
2 2
1 1 0
1 1 2
2 0 1
6
5 5
2 1
| | | | | |
| | |

| | |
| | |
\ . \ . \ .
= =
+

(ii) The position vector of any pt on l
1
=
1
2
1

| |
|
|
|
+
\ .

If l
1
is on
2
, every pt on the line must satisfy the equation
2
1 0
2
| |
|
=
|
|

\ .

r
1 2
LHS 2 1 2 2 2 2 0 RHS
1 2

| | | |
| |
= = + = =
| |
| |
+
\ . \ .

(iii) Vector normal to
1
=
1
1
2
| |
|

|
|
\ .

1 2
1 1
2 2
1
cos
6 9 6

| | | |
| |

| |
| |

\ . \ .
= =

(shown)



2
sin
6
5
6 6
sin 1 cos 1
5 5

=
= = =
d
d




(iv) To show l
1
//
3
, the direction vector of l
1
( b

) must be perpendicular to the normal vector of

3

( n

).

0 1
2 1 2 2 0
1 2
b n
| | | |
| |
= = =
| |
| |

\ . \ .


b n

l
1
//
3


Since l
1
is //
3
(independent of a) and l
1
is the intersection line between
1
and
2
, l
1
must be
on
3
for the 3 planes to have at least one common pt.

To find the value of a, we need just need to use a point on the line l
1
to find the value of the scalar
product of the point with the normal of
3
.

Point on l
1
:
1
0
1
| |
|
|
|
\ .


1 1
0 1 1 2 1 1
1 2
a a
| | | |
| |
= = = =
| |
| |

\ . \ .


(v) Since a -1 and the 3 planes are not // to each other, the 3 planes form a triangular prism.