Escolar Documentos
Profissional Documentos
Cultura Documentos
Dynamic Analysis Equation of Motion
Enviado por
Debasis SahaDescrição original:
Título original
Direitos autorais
Formatos disponíveis
Compartilhar este documento
Compartilhar ou incorporar documento
Você considera este documento útil?
Este conteúdo é inapropriado?
Denunciar este documentoDireitos autorais:
Formatos disponíveis
Dynamic Analysis Equation of Motion
Enviado por
Debasis SahaDireitos autorais:
Formatos disponíveis
Dynamic Analysis
Equation of Motion:
Fig. 1: Body with distributed mass
Consider a solid body with distributed mass as shown in Fig. The displacements
w v u and ,
, stresses
and strains in x, y and z directions are all time depended in dynamic problems. The equation of motion
of the body is obtained by considering both kinetic and potential energies of the body.
The kinetic energy of body is gien by
V
T
dV u u T
!
"
where
# density $mass%unit olume& of the material
u # elocity ector at a point inside the body
'n F(), the entire body is subdiided into number of elements and in each element we express the
displacement u as
Nq u q N u
and hence,
T T T
N q u
*ubstituting into aboe equation, we get the +.( of an element as
,
_
e
V
e T
e
V
T T T T e
q M q q NdV N q dV q N N q T
!
"
!
"
!
"
where M
e
is consistent mass matrix.
The +.( of entire body is obtained by taking summation $i.e assembly& oer all the element and is gien
by
Q M Q T T
T
e
e
!
"
$a&
,e know that, the potential energy of entire body is gien by
F Q KQ Q
T T
!
"
$b&
Then, the equation of motion is obtained by using -agrange equation gien by
.
,
_
Q
L
Q
L
dt
d
$c&
where, T L . *ubstituting of T and from (qn. $a& and $b&, we get
F Q KQ Q Q M Q L
T T T
+
!
"
!
"
Q M
Q
L
( ) Q M Q M
dt
d
Q
L
dt
d
,
_
and
F KQ
Q
L
+
substitute into (qn. $c&, we get
. & $ + F KQ Q M
or F KQ Q M +
For a free ibration of body, . F , then the aboe equation reduces to
. +KQ Q M
$d&
(qn. $d& is equation of motion of body for the free ibration.
Evaluation of Eigen alues and ectors:
,e hae equation of motion of free ibration of body as
. +KQ Q M
$a&
-et the solution of the aboe equation be
t X Q sin
t X Q cos
and t X Q sin
!
sub. 'nto (qn $a&, we get
. sin sin
!
+ t KX t MX
MX KX
!
or MX KX where,
!
$b&
(qn $b& is the expression for eigen alue problem.
(qn.$b& can also be written as
[ ]{ } . X M K $c&
where X is the eigen ector corresponding to the eigen alue .
'f the eigen ector to be nontriial, the required condition is
. M K
$d&
(qn. $d& represents characteristic equation in . *olutions of characteristic equation are the eigen
alues.
For each (igen alue
& , ! , " $ n i
i
there is an (igen ector
i
X
obtained from (qn. $c&.
Then, (qn. $c& is expressed as
[ ]{ } .
i
i
X M K
Derivation of Element Mass Matrices:
!a" For a #$noded bar element:
'n general, the kinetic energy of an
th
e
element can be written as
e
V
e e
T e
dV u u T
!
"
///$a&
The field ariable at any point inside the element is expressed as
Nq u
Therefore, its deriatie w.r.t time, t is written as
q N u
T T T
N q u
*ubstitute into (q, $a&, we get
q NdV N q dV q N N q T
e
V
e
T
e
T
e
V
e e
T T e
,
_
!
"
!
"
q M q T
e T e
!
"
///$b&
where,
e
V
e
T
e
e
NdV N M
is the element mass matrix ///$c&
For a !/noded bar element shown in Fig, we hae,
dx A dV
e e
"
!
. x
e
l x
"
u
!
u
& $x P
e
l
Consider a !/noded bar element as shown in fig, -et u
and
u
!
be the nodal displacements. Treating the material
density,
$kg%m
0
& to be constant oer the element, the
element mass matrix can be obtained from the kinetic
energy functional as follows.
e
{ }
! "
u u q
T
and [ ]
! "
N N N
[ ]
1
1
]
1
'
!
! ! "
! "
!
"
! "
!
"
N N N
N N N
N N
N
N
N N
T
*ubstitute into (q. $c&, we get
dx
N N N
N N N
A M
e
l
e e
e
1
1
]
1
.
!
! ! "
! "
!
"
///$d&
'ntegration of (q. $d& can be carried out using the following integration rule,
e e
e
l
e
l
l l dx N dx N
1
!
&2 " ! $
2 !
!
!
!
"
+
and
e e
e
l
l l dx N N
1
"
& " " " $
2 " 2 "
! "
+ +
*ubstitution of aboe integrals into each term of (q. $d& yields mass matrix for a !/noded bar element as
1
]
1
! "
" !
1
e e e e
l A
M
!b" For a %russ element:
Proceed same as case "a#and show that
e
V
e
T
e
e
NdV N M
///$c&
For a truss element shown in Fig, we hae x d A dV
e e
3 { }
! ! " "
v u v u q
T
and
1
]
1
! "
! "
. .
. .
N N
N N
N $see note below&
&ote: For a truss element we hae
! ! " "
u N u N u + and
! ! " "
v N v N v +
Nq
v
u
v
u
N N
N N
v
u
u
'
1
]
1
'
!
!
"
"
! "
! "
. .
. .
1
1
1
1
1
]
1
1
]
1
1
1
1
1
]
1
! ! "
!
! ! "
! "
!
"
! "
!
"
! "
! "
!
!
"
"
. .
. .
. .
. .
. .
. .
.
.
.
.
N N N
N N N
N N N
N N N
N N
N N
N
N
N
N
N N
T
///$d&
*ubstitute into (q. $c& and carryout integration of each term using the following rule, we get mass matrix
for truss element.
Consider a !/noded truss element as shown in fig. The truss
element can be considered as a bar along its local
coordinate x . -et u
,
v
and u
!
, v
!
be the nodal
displacements in x and y / directions. Treating the material
density,
$kg%m
0
& to be constant oer the element, the
element mass matrix can be obtained from the kinetic
energy functional as follows.
e
"
!
"
u
!
u
"
v
!
v
%russ Element
e e
e
l
e
l
l l dx N dx N
1
!
&2 " ! $
2 !
!
!
!
"
+
and
e e
e
l
l l dx N N
1
"
& " " " $
2 " 2 "
! "
+ +
The resulting mass matrix is
1
1
1
1
]
1
! . " .
. ! . "
" . ! .
. " . !
1
e e e e
l A
M
!c" For a Beam element:
Proceed same as case "a# and show that
e
V
e
T
e
e
NdV N M
///$c&
4ow, for beam element, we hae
dx A dV
e e
3 { }
! ! " "
w w q
T
and
[ ]
5 0 ! "
N N N N N
1
1
1
1
1
]
1
!
5
5 0
!
0
5 ! 0 !
!
!
5 " 0 " ! "
!
"
N
N N N
N N N N N
N N N N N N N
N N
T
///$d&
where, the shape functions for beam element are expressed in cartesian coordinate system as
0
0
!
!
"
! 0
"
e e
l
x
l
x
N +
;
!
0 !
!
!
e e
l
x
l
x
x N +
--- (e)
0
0
!
!
0
! 0
e e
l
x
l
x
N
;
!
0 !
5
e e
l
x
l
x
N +
*ubstitution of (qs. $d& and $e& into (q. $c& and integration of the resulting equation yields the
mass matrix for beam element as
1
1
1
1
]
1
!
! !
5
!! "61 .
0 "0 5
"0 65 !! "61
5!.
e
e
e e e
e e
e e e e
l
l $%mm
l l l
l l
l A
M
&ote: The integration rule used in the preious cases is applicable only for the bar element and
hence it cannot be used for beam element.
'onsistent mass matri(: The element mass matrix obtained by the relation
e
T e
NdV N M
is called consistent mass matrix. 't is termed consistent because the same shape functions 4 are
used to formulate the stiffness and mass matrices. For the !/noded bar element, as an example,
the consistent mass matrix is expressed as,
1
]
1
! "
" !
1
e e e e
l A
M
" !
. x
e
l x
"
e
l
"
w
"
Consider a !/noded beam element as shown in Fig. -et
" "
, w
and
! !
, w
be the nodal deflection and slope
at node " and ! respectiely. Treating the material
density,
$kg%m
0
& to be constant oer the element,
the element mass matrix can be obtained from the
kinetic energy functional as follows.
)um*ed mass matri(: The lumped mass matrix is obtained by equally placing the total mass of
the element at the nodes of the element. Then, the resulting lumped mass matrix is diagonal. For
a !/noded bar element, it is expressed as
1
]
1
" .
. "
!
e e e e
l A
M
.
'onsistent masses v+s )um*ed masses: The lumped masses proide some significant
economies compared to consistent masses. The diagonal lumped mass matrix requires less
storage space than the banded consistent mass matrix. The diagonal lumped form greatly
simplify the matrix calculation, it reduces the number of equations occurring in the dynamic
problem. 7oweer, the mode shapes obtained using lumped mass matrix are less reliable and
consistent mass matrix proides more accurate mode shapes and the natural frequencies than the
lumped mass matrix.
,ro*erties of Eigenvectors:
The (igenectors hae the following properties8
". For a positie definite symmetric stiffness matrix of size $4x4&, there are 4 number of real
&i'envalues and corres(ondin' &i'envectors satisfying the equation $(q. 0.!& MX KX .
!. The eigenalues $i.e. natural frequencies& may be arranged in ascending order8
N
! "
.
and if
N
X X X , , ,
! "
are the corresponding eigenectors $i.e. mode shapes&, then the
following equation will be satisfied,
i
i
i
MX KX . 7ere i mode number corresponding to
i
.
0. The eigenectors are orthogonal with respect to both the stiffness and mass matrices8
.
i iT
MX X
if
) i
.
i iT
KX X
if
) i
5. The lengths of eigenectors are generally normalized so that
"
i iT
MX X
and that aboe normalization of the eigenectors leads to the relation
i
i iT
MX X
Note: Normali*ation o+ the vectors can also ,e done ,% settin' its lar'est com(onent to a (reset
value- sa% unit%. This (rocedure has ,een used while stud%in' natural +requencies and mode sha(es
o+ two or multi ./F vi,ratin' s%stems in mechanical vi,ration.
,rob. 1: 9etermine the eigenalues and eigenectors for the stepped bar shown in Fig. ".
E = 200Gpa, = 7830 kg/m
2
Fig. 1
-olution: 'n general, the elemental stiffness matrix for the bar element is expressed as
1
]
1
" "
" "
e
e e e
l
& A
K
Therefore, for element " and ! it becomes as
! " ! 0
../ m ../ m
1.. mm
#
/. mm
#
F(t)
!
"
". 5 ". 5
". 5 ". 5
: :
: :
"
1
1
]
1
x x
x x
K
and
0
!
". ! ". !
". ! ". !
: :
: :
!
1
1
]
1
x x
x x
K
/// $("&
The general expression for the mass matrix a bar element $(q. 5.0a& is
1
]
1
! "
" !
1
e e e e
l A
M
.
Therefore, for element " and ! it becomes as
" ! ! 0
!
"
"0.6 . . .16!6 . .
.16!6 . . "0.6 . .
"
1
]
1
M
and
0
!
.16!6 . . .0!10 . .
.0!10 . . .16!6 . .
!
1
]
1
M
///
$(!&
Connectiity table8
(lement 4os. -ocal 4ode 4os. ;lobal 9<F 4os.
"
" "
! !
!
" !
! 0
,rite the global 9<F 4os. for the row and column of the elemental stiffness and mass matrices
as shown in (qs. $("& and $(!& and assemble, we get global stiffness and mass matrix as
" ! 0 " ! 0
0
!
"
". ! ". ! .
". ! ". 1 ". 5
. ". 5 ". 5
: :
: : :
: :
1
1
1
]
1
x x
x x x
x x
K
and
0
!
"
.16!6 . . .0!10 . . .
.0!10 . . "=6:6 . . .16!6 . .
. .16!6 . . "0.6 . .
1
1
1
]
1
M
From (q. 0.5, we hae the characteristic equation as
. M K
, where
!
*ubstitution for K and M yields
.
.16!6 . . .0!10 . . .
.0!10 . . "=6:6 . . .16!6 . .
. .16!6 . . "0.6 . .
". ! ". ! .
". ! ". 1 ". 5
. ". 5 ". 5
: :
: : :
: :
1
1
1
]
1
1
1
1
]
1
x x
x x x
x x
.
.16!6 . . ". ! .0!10 . . ". ! .
.0!10 . . ". ! "=6:6 . . ". 1 .16!6 . . ". 5
. .16!6 . . ". 5 "0.6 . . ". 5
: :
: : :
: :
x x
x x x
x x
>pplication of ?oundary condition$s&8 *ince node " is fixed, we hae X
# .. Therefore, modify
the aboe equation using elimination method i.e. eliminate "
st
row and "
st
column of the aboe
equation we get
.
.16!6 . . ". ! .0!10 . . ". !
.0!10 . . ". ! "=6:6 . . ". 1
: :
: :
x x
x x
. & .0!10 . . ". ! $ & .16!6 . . ". ! &$ "=6:6 . . ". 1 $
! : : :
x x x
. ". =6 . 1 ". :6 . 1
"1 @ !
+ x x is the characteristic equation.
The roots of the characteristic equation gie the eigenalues. Therefore, eigenalues are
@
"
". ..6 . " and
@
!
". @ . 1
Therefore, the first natural frequency is
"..!5 ". ..6 . "
@
"
rad%sec or 6 . "6=6
!
"
"
+ 7z.
*econd natural frequency is
@ . 1.:1 . ! ". @ . 1
@
!
rad%sec or 0 . 5"6.
!
!
!
+ 7z.
(igenectors or mode shapes8 >fter modification for the boundary condition, (q. $0.0& can be
written as
.
.16!6 . . ". ! .0!10 . . ". !
.0!10 . . ". ! "=6:6 . . ". 1
0
!
: :
: :
'
1
1
]
1
i
i
i i
i i
X
X
x x
x x
/// $(0&
First )ode *hape8 Take any one equation in the aboe matrix and substitute for
@
"
". ..6 . "
i
,we get first mode shape $i0#.
. & ". ..6 . " .0!10 . . ". . ! $ & ". ..6 . " "=6:6 . . ". $1
"
0
@ : "
!
@ :
+ X x x x X
"
0
"
!
00 . ! .00 . 5 X X or
6:: . .
"
0
"
!
X
X
4ormalization of the aboe mode is obtained by fixing the alue of
"
0
X
# " $a unity&
Then, first mode shape will be,
{ } { } " 6:: . .
"
0
"
!
T
X X
*econd )ode *hape8 *ubstitution of
@
!
". @ . 1
i
into any one equation of (q. $(0& yields
second mode shape.
. & ". @ . 1 .0!10 . . ". . ! $ & ". @ . 1 "=6:6 . . ". $1
!
0
@ : !
!
@ :
+ X x x x X
The aboe equation gies second mode shape as
{ } { } " 6:: . .
!
0
!
!
T
X X
First Mode
-econd Mode
X
x
" ! 0
..6::
"
X
x
"
!
0 ..6::
"
Você também pode gostar
- Exp. 6, Theory Rigid Body EquilibriumDocumento4 páginasExp. 6, Theory Rigid Body Equilibriumdayangmyra100% (2)
- Modeling The Motion of A SpringDocumento5 páginasModeling The Motion of A Springapi-316949577Ainda não há avaliações
- Ab Initio MethodsDocumento19 páginasAb Initio MethodsPrasad Uday BandodkarAinda não há avaliações
- Physics 211 Uniform Circular Motion LabDocumento6 páginasPhysics 211 Uniform Circular Motion Labtham_psdcAinda não há avaliações
- Statistical PostulateDocumento41 páginasStatistical PostulateJoel Aleman RamirezAinda não há avaliações
- Wave FunctionsxOperatorsDocumento3 páginasWave FunctionsxOperatorsSisir BoseAinda não há avaliações
- Mathematical Formula GuideDocumento6 páginasMathematical Formula Guidesayhigaurav07Ainda não há avaliações
- Handout on Tight-binding Calculation for Band StructuresDocumento5 páginasHandout on Tight-binding Calculation for Band StructuresalkeroneAinda não há avaliações
- Moment of InertiaDocumento6 páginasMoment of Inertiarohan_nerlekar794100% (3)
- FEM Notes6Documento16 páginasFEM Notes6Debasis SahaAinda não há avaliações
- Statics Week 1Documento14 páginasStatics Week 1Duaij AlrukaibiAinda não há avaliações
- Coulomb DampingDocumento6 páginasCoulomb DampingAnkush JainAinda não há avaliações
- Antiparticle PhysicsDocumento8 páginasAntiparticle PhysicsHarsha HinklesAinda não há avaliações
- Two MarkDocumento6 páginasTwo MarkpvnandhaAinda não há avaliações
- Particle in A 1D BoxDocumento4 páginasParticle in A 1D BoxJaisurya NanduriAinda não há avaliações
- John Keats' Poem "To AutumnDocumento120 páginasJohn Keats' Poem "To AutumnBrandon HaleAinda não há avaliações
- Buckling Loads For Variable Cross-Section Members With Variable Axial ForcesDocumento9 páginasBuckling Loads For Variable Cross-Section Members With Variable Axial ForcessililloAinda não há avaliações
- Molecular Partition FunctionsDocumento28 páginasMolecular Partition FunctionsAndresLeonardoDiazPalmaAinda não há avaliações
- 10-Linear Strain Triangle and Other Types of 2d ElementsDocumento31 páginas10-Linear Strain Triangle and Other Types of 2d Elementskranthi142434Ainda não há avaliações
- Lab. 3 Rotational Motion: Most Fundamental Concepts Are Substracted From The Web SiteDocumento20 páginasLab. 3 Rotational Motion: Most Fundamental Concepts Are Substracted From The Web SiteTesfaye BelayeAinda não há avaliações
- Simple Harmonic Motion and Oscillations GuideDocumento28 páginasSimple Harmonic Motion and Oscillations Guideshinichi_kesian6117Ainda não há avaliações
- Advanced Computational Fluid Dynamics AA215A Lecture 4: Antony Jameson Winter Quarter, 2012, Stanford, CADocumento21 páginasAdvanced Computational Fluid Dynamics AA215A Lecture 4: Antony Jameson Winter Quarter, 2012, Stanford, CAZakria ToorAinda não há avaliações
- Chapter 1Documento37 páginasChapter 1balls22Ainda não há avaliações
- PHys 21 Physical PendulumDocumento7 páginasPHys 21 Physical PendulumRisa LapolaporekAinda não há avaliações
- Formula FizikDocumento10 páginasFormula Fiziknew_farhanAinda não há avaliações
- Principal: Psychometrika - Vol. 1, No. 1Documento9 páginasPrincipal: Psychometrika - Vol. 1, No. 1phredlovAinda não há avaliações
- Oscillations: ObjectivesDocumento5 páginasOscillations: ObjectivesNanaHanunAinda não há avaliações
- FN MKGGMS: Experiment 2.acceleration of GravityDocumento8 páginasFN MKGGMS: Experiment 2.acceleration of GravityJessica RossAinda não há avaliações
- Finite Element Methods (FEM) : Suzanne Vogel COMP 259 Spring, 2002Documento73 páginasFinite Element Methods (FEM) : Suzanne Vogel COMP 259 Spring, 2002DarmadiAinda não há avaliações
- Pair Production BrezinDocumento9 páginasPair Production Brezin11111__11__1111Ainda não há avaliações
- Transient Analysis in FEA - (New)Documento57 páginasTransient Analysis in FEA - (New)Shreya PatilAinda não há avaliações
- Engineering mechanics statics and dynamics conceptsDocumento6 páginasEngineering mechanics statics and dynamics conceptspvnandhaAinda não há avaliações
- Chapter 1. Quantum Mechanics: NotesDocumento25 páginasChapter 1. Quantum Mechanics: NotesMartín FigueroaAinda não há avaliações
- Aim:-Study of FEM (Finite Element Method) Finite-Element MethodDocumento9 páginasAim:-Study of FEM (Finite Element Method) Finite-Element MethodAshley Silvester AnthonyAinda não há avaliações
- II. Quantum Chemistry and SpectrosDocumento36 páginasII. Quantum Chemistry and SpectrosBilal ParvaizAinda não há avaliações
- (Received 20 July 1999 Accepted For 9 December 1999) : 0093-6413 0t$ - T Mater P L L: I 3 (N) N O ? 8 - 1Documento8 páginas(Received 20 July 1999 Accepted For 9 December 1999) : 0093-6413 0t$ - T Mater P L L: I 3 (N) N O ? 8 - 1Leonardo LagoAinda não há avaliações
- LECTURE 2 - Fluid DynamicsDocumento13 páginasLECTURE 2 - Fluid DynamicsBang AnuhAinda não há avaliações
- Wilson 1990Documento13 páginasWilson 1990Sebastiao SilvaAinda não há avaliações
- Qual Exam Jan2017Documento6 páginasQual Exam Jan2017gasperogandhiAinda não há avaliações
- Normal and Tangential ComponentsDocumento19 páginasNormal and Tangential ComponentsGarrey BrionesAinda não há avaliações
- On The Spin Angular Momentum of MesonsDocumento12 páginasOn The Spin Angular Momentum of Mesonscaruiz69Ainda não há avaliações
- Implementation of A Beam Element in FEA Using MATLAB: (Type The Document Subtitle)Documento12 páginasImplementation of A Beam Element in FEA Using MATLAB: (Type The Document Subtitle)akankshag_13Ainda não há avaliações
- On The Calculation of Consistent Stress Distributions in Finite Element ApproximationsDocumento9 páginasOn The Calculation of Consistent Stress Distributions in Finite Element ApproximationsMekaTronAinda não há avaliações
- 201 Lab 10. Spring Mass OscillationsDocumento8 páginas201 Lab 10. Spring Mass OscillationsMa. YashAinda não há avaliações
- 201 Lab 10. Spring Mass OscillationsDocumento8 páginas201 Lab 10. Spring Mass OscillationsShanice ThompsonAinda não há avaliações
- Chapter 8. Motion in A Noninertial Reference Frame: 8.1 Rotating Coordinate SystemsDocumento13 páginasChapter 8. Motion in A Noninertial Reference Frame: 8.1 Rotating Coordinate SystemsqtmcAinda não há avaliações
- Rotational Dynamics and Aerodynamic ForcesDocumento14 páginasRotational Dynamics and Aerodynamic ForcesdptirkeyAinda não há avaliações
- Project 1Documento13 páginasProject 1Brian KimiecikAinda não há avaliações
- Elasticity ME5413-Lecture1Documento36 páginasElasticity ME5413-Lecture1Parag AhsanAinda não há avaliações
- A Mathematical Theory of Linear ArraysDocumento28 páginasA Mathematical Theory of Linear ArrayssensorseekerAinda não há avaliações
- Symmetric Norm Ideals and Relative Conjugate Ideals: Norberto Salinas )Documento28 páginasSymmetric Norm Ideals and Relative Conjugate Ideals: Norberto Salinas )ceausuAinda não há avaliações
- Solution of The Schrödinger Equation For Trigonometric Scarf Plus Poschl-Teller Non-Central Potential Using Supersymmetry Quantum MechanicsDocumento14 páginasSolution of The Schrödinger Equation For Trigonometric Scarf Plus Poschl-Teller Non-Central Potential Using Supersymmetry Quantum MechanicsanakfisikaAinda não há avaliações
- Statistical Physics (MSC Phy) 1Documento5 páginasStatistical Physics (MSC Phy) 1SACHIN VISHWAKARMAAinda não há avaliações
- Section 2 Electrostatics: Superposition of ForcesDocumento10 páginasSection 2 Electrostatics: Superposition of Forceszeru3261172Ainda não há avaliações
- ORTHOGONAL PROJECTIONS AND MATRICESDocumento6 páginasORTHOGONAL PROJECTIONS AND MATRICESDouglas SoaresAinda não há avaliações
- Mathematical Analysis 1: theory and solved exercisesNo EverandMathematical Analysis 1: theory and solved exercisesNota: 5 de 5 estrelas5/5 (1)
- Understanding Vector Calculus: Practical Development and Solved ProblemsNo EverandUnderstanding Vector Calculus: Practical Development and Solved ProblemsAinda não há avaliações
- Waste EliminationDocumento20 páginasWaste EliminationDebasis SahaAinda não há avaliações
- AB Is A Diameter of A Circle With Centre C (-2,5) - If A (3,-7), FindDocumento3 páginasAB Is A Diameter of A Circle With Centre C (-2,5) - If A (3,-7), FindDebasis SahaAinda não há avaliações
- Savitri - Story of A WomanDocumento3 páginasSavitri - Story of A WomanDebasis SahaAinda não há avaliações
- Hybrid MotorDocumento2 páginasHybrid MotorDebasis SahaAinda não há avaliações
- Addition of Two 8 Bit NumbersDocumento2 páginasAddition of Two 8 Bit NumbersDebasis SahaAinda não há avaliações
- Math QuestionDocumento3 páginasMath QuestionDebasis SahaAinda não há avaliações
- Optimization of Laminate Composite StructuresDocumento18 páginasOptimization of Laminate Composite StructuresDebasis SahaAinda não há avaliações
- What Is Signal ConditioningDocumento2 páginasWhat Is Signal ConditioningDebasis SahaAinda não há avaliações
- FEM Notes6Documento16 páginasFEM Notes6Debasis SahaAinda não há avaliações
- School Stock Register TemplatesDocumento10 páginasSchool Stock Register TemplatesDebasis SahaAinda não há avaliações
- Hybrid MotorDocumento2 páginasHybrid MotorDebasis SahaAinda não há avaliações
- FEM Notes5Documento65 páginasFEM Notes5Debasis SahaAinda não há avaliações
- 01 F7 CB48 D 01Documento38 páginas01 F7 CB48 D 01gsudhanta1604Ainda não há avaliações
- Coal and Petroleum QPDocumento2 páginasCoal and Petroleum QPDebasis SahaAinda não há avaliações
- Arithmetics Part - 1Documento11 páginasArithmetics Part - 1Debasis SahaAinda não há avaliações
- Horizontal Directional DrillingDocumento7 páginasHorizontal Directional DrillingDebasis SahaAinda não há avaliações
- Arithmetics Part - 1Documento11 páginasArithmetics Part - 1Debasis SahaAinda não há avaliações
- Combinations and PermutationsDocumento11 páginasCombinations and PermutationsDebasis SahaAinda não há avaliações
- Sample Home Loan EligibilityDocumento3 páginasSample Home Loan EligibilityDebasis SahaAinda não há avaliações
- Projection of LinesDocumento1 páginaProjection of LinesDebasis SahaAinda não há avaliações
- Topics To Be LearnedDocumento3 páginasTopics To Be LearnedDebasis SahaAinda não há avaliações
- Math - Interest - 1 Test Class IXDocumento4 páginasMath - Interest - 1 Test Class IXDebasis SahaAinda não há avaliações
- Linear Inequation in One Variable - 1Documento5 páginasLinear Inequation in One Variable - 1Debasis SahaAinda não há avaliações
- Cim 2Documento4 páginasCim 2Debasis SahaAinda não há avaliações
- Graphing Linear Inequalities: y MX + B, Etc: Graph The Solution ToDocumento2 páginasGraphing Linear Inequalities: y MX + B, Etc: Graph The Solution ToallenthomasonAinda não há avaliações
- Linear Inequations 3Documento2 páginasLinear Inequations 3Debasis SahaAinda não há avaliações
- CNC Simulation DrawingDocumento2 páginasCNC Simulation DrawingDebasis SahaAinda não há avaliações
- Suffolk Bus S92 Schedule Effective 5-2712Documento2 páginasSuffolk Bus S92 Schedule Effective 5-2712RiverheadLOCAL67% (6)
- Tugas (UTS) ASPK - Andro Tri Julianda (95017019)Documento4 páginasTugas (UTS) ASPK - Andro Tri Julianda (95017019)محمد عزيرAinda não há avaliações
- Stakeholder RegisterDocumento7 páginasStakeholder Registerrouzbehk6515Ainda não há avaliações
- MFS 7104 Quantitative TechniquesDocumento2 páginasMFS 7104 Quantitative TechniquesDavid KAinda não há avaliações
- Particulate Contamination in Aviation Fuels by Laboratory FiltrationDocumento11 páginasParticulate Contamination in Aviation Fuels by Laboratory FiltrationMuhammad KhairuddinAinda não há avaliações
- Unsaturated Polyester Resins: Chemistry and Technology: Piotr Penczek (U) Piotr Czub Jan PielichowskiDocumento2 páginasUnsaturated Polyester Resins: Chemistry and Technology: Piotr Penczek (U) Piotr Czub Jan Pielichowskiae0011979Ainda não há avaliações
- Unit 4 Language Summary: VocabularyDocumento1 páginaUnit 4 Language Summary: VocabularyStephania GalindezAinda não há avaliações
- ECO Report 03Documento96 páginasECO Report 03ahmedshah512Ainda não há avaliações
- Teaching Load FinalDocumento12 páginasTeaching Load FinalEdward BarberAinda não há avaliações
- Hydraulic Vs Mechanical+SnubbersDocumento1 páginaHydraulic Vs Mechanical+SnubbersJordana VeigaAinda não há avaliações
- CSAT 2019 Spe3D Duguid - Andrew PDFDocumento111 páginasCSAT 2019 Spe3D Duguid - Andrew PDFdocturboAinda não há avaliações
- Screen 2014 Nettleton 5 28 PDFDocumento24 páginasScreen 2014 Nettleton 5 28 PDFtaroefAinda não há avaliações
- What Is A BibliographyDocumento7 páginasWhat Is A BibliographyKaye Diamante ValleserAinda não há avaliações
- SampleDocumento13 páginasSamplemypermatakoe71Ainda não há avaliações
- Student's Guide To Year 9 and 10 Science (Stage 5)Documento38 páginasStudent's Guide To Year 9 and 10 Science (Stage 5)dan964100% (1)
- The Function of Composition and InverseDocumento20 páginasThe Function of Composition and InversenormasulasaAinda não há avaliações
- Clearings 2018Documento22 páginasClearings 2018ldxb2001100% (1)
- 660 Inventions That Changed Our WorldDocumento5 páginas660 Inventions That Changed Our WorldKoby RamosAinda não há avaliações
- Resil Mojares Writing About OurselvesDocumento21 páginasResil Mojares Writing About OurselvesSalimAinda não há avaliações
- Certified Lead-Base White Metal AnalysisDocumento2 páginasCertified Lead-Base White Metal AnalysisIshmael WoolooAinda não há avaliações
- Pengadaan Obat Dan Alkes TGL 22 April 2021 Klinik PembantuDocumento8 páginasPengadaan Obat Dan Alkes TGL 22 April 2021 Klinik PembantuIsma Prasetya WardaniAinda não há avaliações
- Electric Current and Ohm's LawDocumento2 páginasElectric Current and Ohm's LawSheldon MillerAinda não há avaliações
- Conflict MangementDocumento35 páginasConflict Mangementmadhuri_bind100% (1)
- Chapter 1 - Notes (Properties of Fluid) PDFDocumento23 páginasChapter 1 - Notes (Properties of Fluid) PDFHappy Ocean100% (1)
- SBC For Toll PlazaDocumento6 páginasSBC For Toll PlazaruchitaAinda não há avaliações
- Physics: PAPER 3 Practical Test InstructionsDocumento8 páginasPhysics: PAPER 3 Practical Test Instructionsmstudy123456Ainda não há avaliações
- Adolescent InterviewDocumento9 páginasAdolescent Interviewapi-532448305Ainda não há avaliações
- Core-Core Repulsion Integrals: E (A Z ZJJDocumento1 páginaCore-Core Repulsion Integrals: E (A Z ZJJRaditya D HmAinda não há avaliações
- The Monkey's PawThe Lady of The Barge and Others, Part 2. by Jacobs, W. W., 1863-1943Documento20 páginasThe Monkey's PawThe Lady of The Barge and Others, Part 2. by Jacobs, W. W., 1863-1943Gutenberg.orgAinda não há avaliações
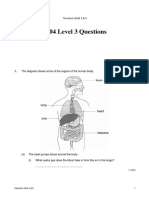
- 2004 Level 3 Questions: Newham Bulk LEADocumento18 páginas2004 Level 3 Questions: Newham Bulk LEAPatience NgundeAinda não há avaliações