1

Scalars and Vectors

Scalars and Vectors
A scalar is a number which expresses quantity. Scalars
may or may not have units associated with them.
Examples: mass, volume, energy, money
A vector is a quantity which has both magnitude and
direction. The magnitude of a vector is a scalar.
Examples: Displacement, velocity, acceleration, electric
field
2
Vector Notation
Vectors are denoted as a symbol with an arrow over the top:
Vectors can be written as a magnitude and direction:
x
r
deg 30 @ C N 7 . 15
o
= E
r
Vector Representation
Vectors are represented by an arrow pointing in the direction of
the vector.
The length of the vector represents the magnitude of the vector.
WARNING!!! The length of the arrow does not necessarily
represent a length.
s m 3 . 2 = A
r
3
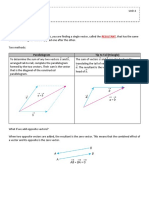
Vector Addition
A
r
B
r
Adding Vectors Graphically.
A
r
B
r
Arrange the
vectors in a head
to tail fashion.
A
r
B
r
The resultant is drawn
from the tail of the first
to the head of the last
vector.
B A C
r r r
+ =
Vector Addition
This works for any number of
vectors.
A
r
B
r
C
r
D
r
D C B A R
r r r r r
+ + + =
4
Vector Addition
Vector Subtraction
A
r
B
r
Subtracting Vectors Graphically.
A
r
B
r
Flip one vector.
Then proceed to
add the vectors
The resultant is drawn
from the tail of the first
to the head of the last
vector.
( ) B A B A C
r r r r r
+ = =
B
r

B
r
5
Vector Components
Example: from the horizontal. Find its
components.
r
r
i r r
x

cos =
r
j r r
y

sin =
r
o
30 @ m 0 . 5 = r
r

( )
i r
i r
x
x

m 3 . 4

30 cos m 0 . 5
o
=
=
r
r
( )
j r
j r
y
y

m 5 . 2

30 sin m 0 . 5
o
=
=
r
r
Any vector can be broken down into components along
the x and y axes.
y x
r r r
r r r
+ =
Vector Addition by Components
You can add two vectors by adding the components of
the vector along each direction. Note that you can only
add components which lie along the same direction.
j s m i s m B A
j s m i s m B
j s m i s m A

7 . 7

7 . 4

2 . 5

5 . 1

5 . 2

2 . 3
+ = +
+ = +
+ =
r r
r
r
s m 4 . 12 = + B A
r r
Never add the x-component
and the y-component
6
Unit Vectors
Unit vectors have a magnitude of 1.
They only give the direction.
i

x
y
z
A displacement of 5 m in
the x-direction is written as
i d

m 5 =
r
The magnitude is 5m.
The direction is the -direction.
Finding the Magnitude and Direction
r
r
x
r
r
y
r
r

2 2
y x
r r r + =
x
y
r
r
= tan

=

x
y
r
r
1
tan
Pythagorean Theorem
7
Vector Multiplication I: The Dot Product
The result of a dot product of two vectors is a scalar!
cos AB B A =
r r
A
r
B
r

1

1

1

=
=
=
k k
j j
i i
0

0

=
=
=
k i
k j
j i
Vector Multiplication I: The Dot Product
( )N

2 k j i F + =
r
( )m

3 k j i s =
r
= s F
r
r
m N ) 3 ( 2 m N ) 4 ( 3 + m N ) 6 )( 2 ( +
m N 6 = s F
r
r
8
Vector Multiplication II: The Cross Product
sin AB B A =
r r
A
r
B
r

0

0

0

=
=
=
k k
j j
i i
j i k
i k j
k j i

=
=
=
The result of a cross product of two vectors is a new vector!
C
r
Vector Multiplication II: The Cross Product
( ) ( ) ( ) B q v B v q B v q
r
r
r
r
r
r
= =
A
r
B
r

C
r
( ) ( ) B A A B C
r r r r r
= =
A C
r r
B C
r r

9
Vector Multiplication II: The Cross Product
( )N

2 k j i F + =
r
( )m

3 k j i r =
r
( ) F r
r
r v
=
( )( )( ) ( )( )( ) ( )( )( ) k i j i i i

m 6 N 2

m 4 N 2

m 3 N 2 + + =
v
( )( )( ) ( )( )( ) ( )( )( ) k j j j i j

m 6 N 3

m 4 N 3

m 3 N 3 + + +
( )( )( ) ( )( )( ) ( )( )( ) k k j k i k

m 6 N 2

m 4 N 2

m 3 N 2 + + +
( ) m N

17

26 + = k j i
v
Vector Multiplication II: The Cross Product
( )N

2 k j i F + =
r
( )m

3 k j i r =
r
( ) F r
r
r v
=
( ) m N

17

26 + = k j i
v
=
v
( ) ( )( ) ( )i

6 3 2 4
( ) ( )( ) ( ) j

2 3 2 6 +

2 3
6 4
j

2 2
3 6
k

3 2
4 3
i

( ) ( )( ) ( )k

4 2 3 3 +
10
Vector Multiplication II: Right Hand Rule
Index finger in the direction of the
first vector.
Middle finger in the direction of the
second vector
Thumb points in the direction of the
cross product.
WARNING: Make sure you
are using your right hand!!!