Pre-Calculus

Mr. Yoon
Period 7
5/24/14
Introduction to Calculus Math Project: 10
Essential Functions of Calculus
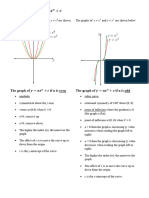
The closer the a term gets to 0, the wider the graph becomes. The further the a term gets from
0, the narrower the graph becomes. When the a term is negative, the graph will result in a sad
face parabola but when the a term is positive, it will result in a happy face parabola.
When b is positive, the graph has a left horizontal shift. The b is what causes the left or right
horizontal shifts.
The c term in this quadratic function determines the vertical shift of the parabola.
Domain: (- to )
Range: (0 to )
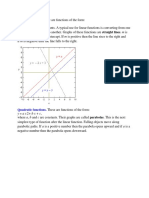
Quadratic Function
Domain: (- to )
Range: (- to )
Cubic Function
When the a value is negative, the graph flips opposite to the original.
As a gets closer to 0, the wider the graph gets and the farther a is from 0, the narrower the
graph results.
When the b term is manipulated, we can see how positive numbers especially those furthest
away from 0 cause the graph to almost look as if it were a linear function However, negative
numbers especially those furthest away from 0 cause the graph to become wider and have a wave
motion.
The c term in this cubic function affects the vertical shift of the graph because it causes to
move down more. We can see this by comparing y=(x+1)
3
-3 and y=x
3.

Logarithmic Function
Domain: (- to )
Range: (- to )
When the a term is negative, the graph of the function is flipped. We see that it still starts off at the
origin but has a downwards vertical shift and then a right horizontal shift.
When the b term is positive, the graph experiences a left horizontal shift. However, when the b
term is negative, the graph experiences a left horizontal shift on the x axis but heads towards the right.
When x is negative, the graph shifts opposite of the original.
When the c term is negative, the graph experiences a right horizontal shift on the x axis. To show
this, the last logarithmic function shows how the -2 determines the downward shift.
Domain: (- to )
Range: (- to )
Rational Function
Domain: (- to )
Range: (- to )
When the a term is negative, it mirrors the original graph.
As a increases from 0 (positive #s) or decreases away from 0 (negative #s) the curve of the
graph gets further away from 0.
The h term is where the graph will cross vertically on the y-axis. However, when h is
negative, the graph experiences a left horizontal shifts and when h is positive, the graph
experiences a right horizontal shift.
The k term in the equation above represents the number that the graph will never cross or
touch.

Trigonometric Function
The a term in this trigonometric function represents the asymptote of the graph. For instance,
if a is positive 4, the asymptote of the graph is 4.
The b term stands in this trigonometric function represents the period of the graph.
The c term in this trigonometric function begins the sine function graph. The trigonometric
function of 2sin2x+2 shows how the number 2 displays the sine graph at its highest (asymptote).
Domain: (- to +)
Range: (- to +)
Trigonometric Function
When a (asymptote) is negative, the graph turns into a negative cosine. To further explain this, we
can see y=-2cosx-1 where -2 causes the cosine to have the same wave motion as a regular cosine
graph but on the negative side. A regular cosine graph would begin at the highest point or lowest
point (asymptote) depending on the type of number it would be (- or +).
The b term is the period of the graph. In other words, if our period is 2(pi) then the graph ends at -
2(pi) and 2(pi).
The c term which is exemplified as y=-2cosx-1 starts the sine function. We can see how the -2
causes the graph to have a space of 2 before hitting the x axis again. The -1 which is c causes the
function to be flipped upside down (-cosine) and therefore everything is inverse. If it was a positive
1, then the function would be over 0 in the positive side of the graph.

Domain: (-3 to 1)
Range: (- to +)
Rational Function
When the a term is negative, it mirrors the original graph.
As the a term increases from 0 (positive #s) or decreases away from 0 (negative #s) the curve of
the graph gets further away from 0.
The h term in the equation above represents where the graph will cross vertically on the y axis.
However, when h is positive, theres a left horizontal shift and when the h is positive, theres a
right horizontal shift.
The k value in the equation above represents the number that the graph will never cross or touch.

Domain: (- to +)
Range: (- to +)
Domain: (- to +)
Range: (- to +)
Absolute Value Function
The x is our "a" value. The "a term can The first absolute value function portrays x as our "a" value.
The "a" value in this case can be substituted by a given value. This value can either be positive or
negative. We can see that as x is a negative value, the y results in a mirrored image of the x value.
However, we have to keep in mind that this mirrored image is always the result of x giving us a positive
y value.
The second absolute value function portrays x+1 as our "b" value. When x+1 is our "b" value, we see
that the graph of the function turns out to be heading in the same direction as the previous function.
However, the graph experiences a left horizontal shift.
The third absolute value function exemplifies +1 as our "c" value. The "c" value which is +1 causes the
graph to have a vertical shift upwards. The a graph is almost as accurate as the first absolute value
function because it kind of mirrors the graph. However, since it is negative outside of the absolute value,
the graph is pointing up. The "c" causes the graph to be raised up within the y axis.
The fourth absolute value function is an example of how the outside value affects the graph. This outside
value can be said to be "a" because it affects the x in the absolute value itself. The graph is compressed
and is narrower. When we look at the table, we see that when x is negative or positive , it gives a
positive y value. For example, x=2 and x=-2 but y will equal 6 for both x values.

Domain: (- to +)
Range: (- to +)
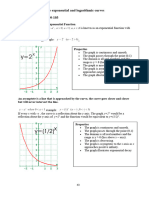
Exponential Function

The first exponential function portrays the usage of "a" as positive 2. We see that when "a" is positive
two, the graph gets closer to the x-axis and once it crosses the y-axis, the graph rises. When the x values
get closer to 0 from negative to 0, the y values result in decimals such as 0.25 and 0.5 but they never
touch the x-axis. We can see how positive 2 which is "a" determines the direction of the graph.
The second exponential function portrays the usage of "a" as negative 2. We see that when "a" is a
negative number, the graph gets closer to the x-axis like in the previous function. When the x values get
closer to 0 from negative to 0, the y values result in decimals such as 0.25 and 0.5 but they never touch
the x-axis. We can see how negative 2 which is "a" determines the direction of the graph.
The third exponential function portrays the usage of "b" in addition to "a" which is 2 or -2 according to
previous functions. We see that since "a" is positive, the graph will go in an upward direction displaying
the same sort of shape that the previous positive 2 graphs displayed. The addition of "b" as 3 causes the
graph to move vertically upwards and although we cannot see in the graph demonstrated, the horizontal
destination of the graph will end up very close to the x-axis but will never touch the x-axis itself.
Logarithmic Function

Domain: (- to +)
Range: (- to +)
In the first logarithmic function, we have the number 2 representing the "a" value in which
we see the graph get close to the y-axis. As we to below 0, the more frequently y will be
undefined.
In the second logarithmic function, we see how when "a" is a negative number, y is undefined
because the "a" value can only be a positive number or else it will remain undefined.
In the third logarithmic function, we see how "b" affects the graph because since "b" is
characterized as (x+2), the function shifts to the left and drifts away from the y axis only
crossing the x-axis.
In the fourth logarithmic function we see how when "c" is added, the graph crosses the x axis
earlier since there is a -3 in the function. We can see that when the x values get closer to 0,
the y values are negative or undefined. However, when the x values get beyond zero, the y
values increase from negative to positive values.