Study Advice Service

Mathematics
Worksheet
Logarithms
This is one of a series of worksheets designed to help you increase your confidence
in handling Mathematics. This worksheet contains both theory and exercises which
cover:

1. Revision of Indices 2. What are Logarithms?
3. Rules for manipulation 4. Solving equations using logarithms
. !he straight line la" #. $raph of lnx and its inverse
There are often different ways of doing things in Mathematics and the methods
suggested in the worksheets may not be the ones you were taught. !f you are
successful and happy with the methods you use it may not be necessary for you to
change them. !f you have problems or need help in any part of the work then there
are a number of ways you can get help.
"or students at the #niversity of $ull
Ask your lecturers
%ontact the Study Advice Service in the &rynmor 'ones (ibrary where you can
access the Mathematics Tutor) or contact us by email
%ome to a *rop!n session organised for your department
(ook at one of the many textbooks in the library.
"or others
Ask your lecturers
Access your Study Advice or Maths $elp Service
#se any other facilities that may be available.
!f you do find anything you may think is incorrect +in the text or answers, or want
further help please contact us by email.
Tel: 01482 466199
Web: www.hull.ac.uk/studyadvice
Email: studyadvice@hull.ac.uk
0
1. Revision of Indices
a% (ogarithms are really indices so understanding indices and how to manipulate
them will help you to deal with logarithms.
Section b, shows why the rules of indices work - basically because we define them
to work in the way we want them to. !t will help you sort out logarithms if you
understand why we define the rules of indices in the way we do.
!f you are really in a hurry you could skip section b, and go straight to section c,
which starts with the list of rules.
&% !he rules of indices
This section is taken from the booklet Algebra /.
!f
m
and
n
are positive integers and 0 a ) then
n m n m
a a a
+

n m n m
a a a

+if
m n >
) and ( )
mn
n
m
a a

this means
! 4 ! 4
x x x x
+
1
10 6 4 6 4
" " " "
+
1
" ! 8 ! 8
y y y y

etc.
That2s 34 but what about other values of the indices +the
m
and
n
above,
%onsider #
"
!
x
x
expanding gives
2 "
!
1
x
x x x x x
x x x
x
x

!f the 5rule2 works

2 " ! " !
"
!

x x x x
x
x
So "e define
2
x

to be
2
1
x
%onsider #
"
"
x
x
expanding gives 1
"
"

x x x x x
x x x x x
x
x

!f the 5rule2 works
0 " "
"
"
x x
x
x


So "e define
0
x to be /
%onsider
/
6
x
we know
x x x
+for instance 9 ! ! 9 9 etc.,) so
!f the 5rule2 works
/ /
/
6 6
x x x x
So "e define
x x
2
1
7ote for x to exist 0 x > as you can2t take the s8uare root of a negative number.
We extend the meaning and use of indices by defining +for 0 x > ,
n
n
x
x
1
as

)
n
x x
n
as
1
and
0
x as /.
!t is important to realise that these rules fit what we know for positive integers and are
defined to be true for all indices +positive) negative or fractional,.
c% Summar' of the rules(
1
"or all values of
a
+where 0 a > $
n m n m
a a a
+
%i$
n m n m
a a a

%ii$
( )
mn
n
m
a a %iii$
n
a a
n
1
%iv$
%ombining the last two means that
( )
m
n
a
n
m
a a
n
m
"or practice on these rules see Algebra / exercises 9 and :.
2. What are Logarithms?
!f
x
a y then we introduce the inverse function logarithm and define
x y
a
log
+read as log base
a
of
y
e8uals
x
,.
or
x y a y
a
x
log
Where means ;implies and is implied by< i.e. it works both ways.
7ote this means that) going from exponent form to logarithmic form:
100 10
2

2 100
10
, + log
01 . 0 10
2

2 01 0
10
, . + log
1 10
0

0 1
10
, + log
!2 2
"
" !2
2
, + log
! 9
2
1

2
1
9
! , + log
4 8
!
2

2
8
!
4 log + ,
And in going from logarithmic form to exponent form:
1 10
10
, + log
10 10
1

! 001 0
10
, . + log

001 . 0 10
!

0 1
2
, + log
1 2
0

4 81
!
, + log
81 !
4

2
1
100
$ 10 % l&'

10 100
2
1

2
!
"
" " , + log

" " "
2
!

!n practice we use) mainly) logs base

e
+ 6.=/>... e , and) occasionally base /0.
3n your calculator you should find a button labelled (3? with the 6
nd
function
/0
x

and a second button labelled (7 +or ln, with the second function
x
e
.
!f you put /.9: into your calculator) find
/.9:
/0
and then find the (3? of the answer
you should get back to /.9:. This works for any number you choose.The reverse
also works +except for 0, if you find the (3? first and then /0 to the power of the
answer. @ou get the same results when using the (7 button.
x
use
/0
x
button
then (3? button
use
x
e
button
then (7
button
/.9: 6>./>A>A6BA/ /.9: 9.6CA//9:/: /.9:
0.6:9 0.::=/>:=9>B 0.69: 0.==:CB/>06 0.6:9
Try a few numbers for yourself.
)*ercise 1
/. Write the e8uivalent logarithmic form for the following
062" . 0 4 $ % " 12" $ % 24! ! $ % 10000 10 $ %
2 " 4
!
1


iv iii ii i
2
6. Write the e8uivalent exponent form for the following
4 0016 0 8 ! 64 6 1000000
"
4
1
4096 4 10
. log , + log , + log , + , + log , + iv iii ii i
A. ?iven that 2 10
!010" . 0
write down the values of
200 2
10 10
log , + log , + ii i
9. #se your calculator to write down the values of the following
124" 0 124" 0 2!4 2!4 . ln , + . log , + ln , + log , + iv iii ii i
3. Rules for the manipulation of logs
Demember in
x
a y the
x
is an index and as
y x
a
log
this is why logs work like
indices.
+roofs of the rules
+i, ?iven
x
a p and
y
a q then
y x y x
a a a pq
+

&y the definition
x
a p p x
a
log
y
a q q y
a
log
So
q p y x
a a
log log + +
&ut
y x
a pq
+
( ) pq y x
a
log +
This shows that
( ) q p y x pq
a a a
log log log + +
+ii, !n the same way we can show that
q p
a a
q
p
a
log log log
,
_

+iii, ( ) p n p
a
n
a
log log
&y the definition
x
a p p x
a
log
Also ( )
nx
n
x n
a a p ( )
n
a
p nx log
$ence ( ) p n nx p
a
n
a
log log
!he rules are(
q p pq
a a a
log log , + log +
q p
a a
q
p
a
log log log
,
_

( ) p n p
a
n
a
log log
@ou can check some of these on your calculator. Take various values of
a
and b
and) using either the log button or the ln button) compare the values of
b a log log +
with
, log+ab
)
b a log log
with
, log+
b
a
l) , log+
b
a with
a blog
.
#sing logs base /0
a
b ab
logab loga logb + log log a b
: =.6 AC /.::CA 0.CBB0 0.>:=A /.::CA
A.6 /.B C.0> 0.=>AB 0.:0:/ 0.6=>> 0.=>AB
a
b
a
b
( )
log
a
b
loga logb log log a b
: =.6 0.CB90 0./:>9 0.CBB0 0.>:=A 0./:>9
!
A.6 /.B /.C>96 0.66C9 0.:0:/ 0.6=>> 0.66C9
,er' Important -otes #sing p x a p
a
x
log .
/. Eutting 0 x ) 1 0 1
0
a
a p log i.e. the log +any base, of / is Fero.
6. Eutting / x ) a a a p
a
log 1
1
hence
1 10 1
10
log ) lne
etc
A. Taking logs base
a
of both sides gives ( )
x
a a
a p log log but as
p x
a
log
so we have ( ) x a
x
a
log for any base.
9. Eutting
p x
a
log
into
x
a p gives
p
a
a p
log
or p a
p
a

log
.
:. As 0 a > then for all values of
x
,
x
a
is positive and) as
x
p a
then
0 p >

for all
x
) then we can only take the log of a positive number.
Examples +Where the 8uestion says log) this implies
log
a
where 0 a >
/. Write as single logarithmic terms
+i,
4 log log +
:
28 4 4 log , log+ log log +
+ii,
" !log
:
A
Alog: log+: , log/6:
+iii,
2"
2
1
log
: " 2" 2" 2"
2
1
2
1
log log log log
+iv, -logC :
( )
6
1 1
6 6 1 6 log log log log

6. Simplify
( )
b
d !
log
:
( ) ( ) b d b d
b
d
log log log log log log + ! !
!
A. Simplify ( ) : ln
kx
ce ( ) ( ) kx c e kx c e c ce
kx kx
+ + + ln ln ln ln ln ln
9. Simplify 6 2 " ! 2 4 ! ln ln ln ln + :
!
! 2 2
! 2
6 2
! 4
6 2 ! 4 6 2 " ! 2 4 !
"
2 6
"
2 !
" 2 !
ln ln ln
ln ln ln ln ln ln ln ln

,
_

,
_

+ +
The answer ! ln may be more suitable than the /.0>BC that the calculator gives.
)*ercise 2
/. Gxpress the following in terms of
log p
)
logq
and
logr
+i,
log+ , pqr
+ii,
6
log+ , p
+iii,
( )
log
p
r
+iv,
( )
/
log
q
+v, log r +vi, log qr
6. Write as single logarithmic terms
+i,
log: logA +
+ii,
log6C log6
+iii,
9logA
+iv,
!6
2
1
log
+v,
A
log9 :log6
+vi,
log9 log/6 log> +
+vii,
AlogC log9 6logA
.
A. Simplify +some answers have a log term,
+i, ( )
4
10
10 ! log +ii,
C
ln+ , e
+iii,
2 ! 2
!
2
4
1
log log log +
+iv,
A 6
ln+> , ln+A , ln+C , x x x +
+v,
( ) ( ) ( ) x x x 4 ! 2 16
2
! 2
4
1
log log log +

4
4. Solving equations using logs
Examples
+i, Solve the e8uation 9 . ! 10
x
The definition of logs says if
x
a y then
x y
a
log
or y x a y
a
x
log
$ence
/0
/0 A.=B log A.=B 0.:=>C9
x
x +to : decimal places,
%heck 9000 . ! 10
"864 . 0
+to : decimal places,
!n practice from 9 . ! 10
x
we take logs to base /0 giving
( ) ( )
( ) ( )
"864 0
9 ! 10
9 ! 10
10
10
.
. log log
. log log

x
x
x
+ii, Solve the e8uation "6 !
2

x
( ) ( )
( ) ( )
( )
( )
.... .
... .
log
log
log log
log log
8!201 1
6640! !
!
"6
2
"6 ! 2
"6 !
10
10
10 10
10
2
10

x
x
x
x
%heck
A
A 6=
)
9
A >/
) we want
6
A
x
so the value of 6x lies between A and 9 or
A 6 9 x < < which means
x
lies between /.: and 6.
This tells us that /.>A60/... x is roughly correct.
+iii, Solve the e8uation
/
9 A
x x+

( )
( )
.. .
log log
log
log log log
log log log
log log
log log
8188 !
! 4
!
! ! 4
! ! 4
! !
! 1 4
! 4
10 10
10
10 10 10
10 10 10
10 10
10 10
1

+
+

+
x
x
x x
x
x x
x x
%heck

'

+
24! ! ! !
2"6 4
" .. 8188 . 4 1
4
x
x
9 9
A.>/>>..
very close.
7ote you could combine terms) giving)
( )
.. .
log
log
log log
log
8188 !
!
! 4
!
!
4
10
10
10 10
10

x
"
+iv, Solve the e8uation
x x 2 " 6
! 4
+

Take logs of both sides

Gxpand brackets
%ollect terms
"actorise the left hand side
divide
( ) ( )
( )
0.=>>6:
log log
log log
log log log log
log log log log
log log log log
log log

+
+
+
+

+
! 2 4
4 6 ! "
4 6 ! " ! 2 4
4 6 ! " ! 2 4
! 2 ! " 4 6 4
! 2 " 4 6
! 4
2 " 6
x
x
x x
x x
x x
x x
+7ote you get the same answer by using the ln button on your calculator.,
%heck !68 . 1!! 4 4 4
211" . " 6 882" . 0 6

+ + x
and
!68 . 1!! ! ! !
$ 882" . % 2 " 2 "

C.:=C9B> x
7otice that you could combine the logterms in

! 2 4
4 6 ! "
log log
log log
+

x
to give
( )
( )
2
6 "
! 4
4 !

log
log
x
!t does not really simplify things here but) in some cases) it can.
+v, Solve the e8uation ( ) ( )
1 2 1
" 2 !
+

x x
Take logs of both sides
Gxpand brackets
%ollect terms
"actorise left hand side
simplify
divide
( ) ( )
( ) ( )
( ) ( )
( ) ( )
( )
( )
686!1 0
920819 0
6!202! 0
" 2 !
! " 2 " 2 !
" " 2 2 ! !
" 1 2 2 ! 1
" 2 !
2"
!

!0

!0
2"
!

! " 2
1 2 1
.
.
.
log
log
log log
log log log
log log log log log log
log log log log log log
log log log log

+ +
+ + +
+ + +

+
x
x
x
x x
x x
x x
x x
%heck +not easy..,
($S H
( )
9

! !
2
. 1 1

x
+taking 9 ! !
2 . 1
,
D$S H
( ) 1
"
2
"
2
" 2 " 2
4 . 0
4 . 0 1 2

+ x
+taking ... 2 . 2 " " "
" . 0 4 . 0
,
The values of ($S and D$S are roughly the same. A more exact check could be
made using a calculator.
6
)*ercise 3
Solve the e8uations
/. 6 !
x
6. 4 "
x
A. " 2
2

x
9. !
1

y
:. ! 4
1 2

+ a
C.
p p ! 1 1 2
" 6
+ +
=. ( ) "
!
2

s
>. ( ) ( ) 128 2 2
2 ! 1

+ r r
B.
4 ! 2 !
! "

s s
/0. ( ) ( )
x x ! " 2 "
4 9 "

. !he straight line la"

There are many uses of logs. They are fre8uently re8uired in %alculus and also
occur when analysing data from experiments.
!n an experiment the following results were obtained.
x
6 9 : C.: > //
y
9 /0 /A /B.6 6A A=
*rawing a graph of values of
y
against
x
gives a curve but it is not possible to give
its e8uation. !.e. it is not possible to find the function which will give other values of
y
for given values of
x
. !t is possible to estimate values from the graph.
!t is suggested that the graph of the function may be of the form
n
ax y .
!f we take logs +base
e
, though you could use base /0, of both sides.
( ) x n a ax y
n
ln ln ln ln +
!f we put
a A x X y Y ln and ln ) ln
this becomes nX A Y + which is the usual
e8uation of a straight line.
x
6 9 : C.: > //
y
9 /0 /A /B.6 6A A=
ln X x 0.CB /.AB /.C/ /.>= 6.0> 6.90
ln Y y /.AB 6.A0 6.:C 6.B: A./9 A.C/
&y drawing a straight line which fits the points
as closely as possible we can get approximate
values for A and
n
.
The e8uation is nX A Y +
The intercept is at 0.= A which gives
ln 0.= 6.0/9 a a
The gradient is found by taking two points and
using
?radient H
1 2
1 2
X X
Y Y

Take A+6.:) A.=,) B+0) 0.=,

?radient AB
2 . 1
0 " . 2
. 0 . !

The gradient /.6 n .

The formula is +approximately,
2 . 1
2x y .

I
1
!
1
2
!

2 1
"rom the graph the point +0.CB) /.AB, could be an error in a reading.
)*ercise 4
"ind the values of the unknowns given the following sets of readings
/. !t is assumed that the connection is of the form
n
ax y
x
0.: 6 A : :.C >
y
/./ >.: /:.C AA.: AB.> C=.B
6. !t is assumed that the connection is of the form
n
ax y
x
/.A /.= 6 A.C 9.A C
y
>/ :9 96 /=.C /A.: >.6
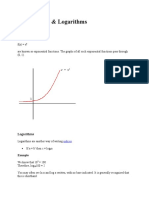
# !he graph of y / lnx and its inverse.
*rawing the graphs of
x
e y and
x y ln
using the same scale on the axes shows that
one is the reflection of the other in the line
x y
. This fits with the definition of one
being the inverse of the other.
Take
x
e y ) interchanging
x
and
y
+which
gives the inverse function, gives
y
e x )
take logs base
e

y x ln
0ns"ers
)*ercise 1
/,
2 062" 0 " " 24! 4 10000
4
!
1
12" ! 10
. log , + log , + log , + , + log , + iv iii ii i
!010" 2 !010" 0 ! 0016 0 0016 0 "
8 4096 8 4096 64 4 1000000 10 2
4
4 ! 6
4
1
. , + . , + , . or . , +
or , + , + , + ,
9
:
/
ii i iv
iii ii i

9,
08!4 . 2 $ % 9048 . 0 $ % 4""! . " $ % !6921 . 2 $ % iv iii ii i
8
y ( e
x
y ( lnx
1
1
x
y
y=x
)*ercise 2
r q vi r v q iv
r p iii p ii r q p i
log log , + log , + log , +
log log , + log , + log log log , + ,
2
1
2
1
2
1
2 1
+
+ +
6 6 2 6 81 1! 1" 2 log , + log , + log , + log , + log , + log , + log , + , vii vi v iv iii ii i
( ) ( )
9
16
2
10
2 2 6 ! 4 ! log , + ln , + log , + , + log , + , v x iv iii ii i +
)*ercise 3
/, /.CA0B 6, 0.>C/9 A, /./C/0 9, 6.==/6 :, -0./0A>
C, 0./9C: =, A.BCB9 >,6 B, /.9/:= /0, 0.==00
)*ercise 4
/, A) /.: 6, /60) /.:
We would appreciate your comments on this worksheet) especially if
you2ve found any errors) so that we can improve it for future use.
Elease contact the Maths tutor by email at studyadviceJhull.ac.uk
Updated 30
th
November 2004
The information in this leaflet can be made available in an
alternative format on re8uest. Telephone 0/9>6 9CC/BB
K 600B
9