Dr.

Utzerath,

MATH 2451Brannan and Boyce, Section 1.1

Mathematical Models, Solutions, and Direction Fields

Page 1 of 7

Assigned problems, pp. 14-15: #3 (MATLAB printout due in class Jan. 21 (MW class) or Jan. 22,
(TTh classes); see p. 7 of this lecture), #7, #11, #14, #15, #17, #19.

What does it mean to solve a differential equation?

In solving a differential equation we try to find a function of the dependent or unknown
variable. Since the solution is a function, it needs to be defined on some interval of the
independent variable.
We have already defined a solution of an nth-order ordinary differential equation to be a
function y = (t) that possesses at least n derivatives that are continuous on some tinterval I, which, when substituted into the ODE, reduces it to an identity on I. If the
solution of an nth-order ODE exists as a function y = (t) with n continuous
derivatives, we say that the ODE has an analytic solution.
Some issues:
Not every differential equation can be solved for an analytic solution.
Sometimes we have to use numerical methods or geometrical methods to find
approximations to the solution or solutions.
Even if we find an analytic solution, we still have to apply or interpret the solution
so see if it makes sense in light of the original problem.
SOLUTION CURVES AND FAMILIES OF SOLUTIONS
The graph of a solution of an ODE is called a solution or integral curve.
Just as when we take an anti-derivative we use a constant c of integration, so when we
solve a 1st-order ODE (, , ) = 0, we usually obtain a solution containing a single
arbitrary constant or parameter c. This means that a single differential equation can
possess an infinite number of solutions corresponding to the unlimited number of choices
for the arbitrary constant.
Example 1. Solve the ODE, = 2 to obtain a one-parameter family of solutions.
Graph several of the infinitely-many solution curves.

Section 1.1, Page 2 of 7

General solution
Note that when an analytic solution of a first-order ODE exists, it is a one-parameter
family of solutions. The analytic solution of a second-order ODE is a two-parameter
family of solutions. The analytic solution of an nth-order ODS is an n-parameter family
of solutions. If the n-parameter family of solutions contains every possible solution of the
differential equation, we call it a general solution. The analytic solution of every
linear ODE is a general solution.
IVPs and Particular Solutions
When solving an ODE, we can obtain a solution that has no arbitrary parameters by
specifying a condition (or conditions) that the solution must satisfy. The conditions are
referred to as initial conditions if they all refer to same initial value of t0. If the
conditions do not refer to the same value of t, they are referred to as boundary
conditions.
An Initial Value Problem (abbreviated IVP) refers to a differential equation together
with enough initial conditions to find values for all of the n arbitrary parameters in the
family of solutions. A first-order IVP consists of a first-order ODE together with one
initial condition,(0 ) = 0 . A second-order IVP consists of a second-order ODE
together with two initial conditions: (0 ) = 0 , (0 ) = 1. An nth-order IVP consists
of an nth-order ODE together with n initial conditions: (0 ) = 0, (0 ) = 1 , . . . ,
(1) (0 ) = 1 . The solution of an IVP is referred to as a particular solution.
Particular solutions are free of arbitrary parameters.
Example 2. In Example 1 we sketched several geometrical curves of the one-parameter
family of solutions of = 2. In fact, because = 2 is linear, the one-parameter
family is a general solution. Each of the geometrical curves of the family is an integral
curve associated with a particular value of the parameter c.
a) What is the particular solution of the IVP, = 2, (0) = 3?

b) Sketch its integral curve.

c) What point must the integral curve pass through?

d) What is the slope of the tangent line to the integral curve at this point?

Section 1.1, Page 3 of 7

CONSTANT SOLUTIONS OF FIRST-ORDER ODES.

We refer to = (, ) or = (, ) as the normal form of a first order ODE.

The expression (, ) is often referred to as the rate function.
Constant solutions of = (, ) are the zeros of the rate function. Constant
solutions have the form () = .
2
Example 3. Put the ODE 2 = in normal form. Find the constant solution(s) of
2 =

GEOMETRIC METHOD OF VISUALIZING SOLUTIONS OF = (, ).

DIRECTION FIELDS
Given = (, ). One geometric way of visualizing solutions to is to use the fact
that (0 , 0 ) gives the slope of the tangent line to the solution y at the point (0 , 0 ). By
sketching a lot of little tangent segments we can obtain a direction field (or slope field).
Example 4: a) For the differential equation,
= , calculate the tangent slopes
for the points in the table. Check your
calculations against the tangent slopes
shown in the Maple printout below.

t
0
1
1
0

y
0
0
0
2

Tangent slope

b) Sketch solution curves that pass through the points

y(1) = 1

y(0) = 1

y(1) = 1

AUTONOMOUS FIRST-ORDER ODEs AND EQUILIBRIUM SOLUTIONS

An ODE in which the independent variable does not appear explicitly in the expression
for is said to be autonomous. If the symbol t denotes the independent variable, then

an autonomous first-order differential equation can be written as = (). We will

assume that the function f and its derivative f are continuous functions of y on some
interval I.
Check your understanding

Which of the following equations are autonomous?

dy

y2
a) = ( )
b)
c) y ' y x
dt

Section 1.1, Page 4 of 7

Equilibrium Solutions
Constant solutions of autonomous differential equations are referred to as equilibrium
solutions. If solutions on either side of (above and below) an equilibrium solution
converge to the equilibrium solution, we say that the equilibrium solution is stable. If
solutions on either side of the equilibrium solution diverge from the equilibrium solution,
the equilibrium solution is unstable. If solutions on one side converge to the equilibrium
solution, but diverge on the other side, we say that the equilibrium solution is semistable.
Determining the behavior of solutions of autonomous first-order ODEs.

Example 4. Given = (). What do we know about the behavior of y when y' is
positive? When y' is negative?

Example 5. Write a first-order autonomous

ODE in the form = + that has a
stable equilibrium solution at y = 5.
Sketch the equilibrium solution and show
the behavior of solutions above and below it.

Example 6. Consider the ODE, = 3 + 5 2 6.

a) Find the equilibrium solutions of = 3 + 5 2 6.

b) On what y-intervals are the solutions of = 3 + 5 2 6 increasing and

decreasing?

Section 1.1, Page 5 of 7

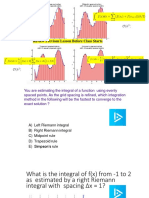
c) Determine which direction field below corresponds to = 3 + 5 2 6.

A
B

d) Determine the long range behavior of solutions of = 3 + 5 2 6 in the

following cases:
For 2 < y0 < 3, lim () = _____

For y0 < 0, lim () = _____

For y0 > 3, lim () = _____

d) Classify the equilibrium solutions as stable, unstable, or semi-stable.

Models Leading to First-Order ODEs

Differential equations are often used to describe some real-life system or phenomenon.
The mathematical description of a system of phenomenon is called a mathematical
model. The process of obtaining a mathematical model involves: (1) identifying
variables and making reasonable assumptions (that may include empirical laws); (2)
formulating the model, often in terms of rates of change (derivatives); (3) testing the
model through solving; and (4) possibly modifying the model in light of results obtained.

Words that lead to derivatives in differential equations include the following:

Section 1.1, Page 6 of 7

" rate of change of "

" rate of increase/decrease of
all of these indicate a derivative
" velocity"

" acceleration"
Other words or relationships of interest:
is
means
equal
A is (directly) proportional to B means A = kB, where k is the constant of
proportionality

A is inversely-proportional to B means =

The Field Mouse problem (see Example 3, pp. 8 9 of text)

One of the simplest models of population growth, called the Malthusian model of
exponential growth, was derived by the British economist Thomas Malthus (1766-1834)
who first observed that many biological populations increase at a rate proportional to the
current population.
Example 8. In the absence of predators a population of field mice inhabiting a certain
rural area grows at a rate proportional to the current population, p(t). Specifically, the
growth rate is 0.5/month. Initially there are 950 mice. Set up an IVP to model the
growth of the field mouse population. What will its solution tell us?

Example 9. a) Modify the model of Example 8 to include the fact that owls in the area
kill 15 mice/day. Express the modified model as an IVP.

b) Without solving, graph the solution of this IVP in

the direction field to the right and express its longterm behavior (the behavior of the solution as t
) as a limit.

c) Identify the equilibrium solution of the model of part b). Is the equilibrium solution
stable or unstable? What does the equilibrium solution tell us about the mice/owl
ecosystem (according to this model)?

Section 1.1, Page 7 of 7

Example using MATLAB to create direction fields

>> % Section 1.1 #2, y'=2y-3
>> % First set y'=0 to find the equilibrium solution y = 3/2.
>> % Set the y-range in meshgrid so that it shows values above and below y = 3/2
>> [X,Y]=meshgrid(0:0.2:4,-1:0.2:3);
>> S=2*Y-3;
>> L=sqrt(1+S.^2); % L is used to scale the arrow lengths
>> quiver(X,Y,1./L,S./L), axis tight, xlabel('t'), ylabel('y')

3
2.5
2

1.5
1
0.5
0
-0.5
-1
0

0.5

1.5

2.5
t

3.5