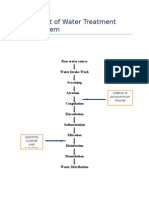
Escolar Documentos
Profissional Documentos
Cultura Documentos
Bernoulli Equation Derived
Enviado por
Vivian ChouDireitos autorais
Formatos disponíveis
Compartilhar este documento
Compartilhar ou incorporar documento
Você considera este documento útil?
Este conteúdo é inapropriado?
Denunciar este documentoDireitos autorais:
Formatos disponíveis
Bernoulli Equation Derived
Enviado por
Vivian ChouDireitos autorais:
Formatos disponíveis
Bernoulli equation for incompressible, smooth fluid flow.
http://www.4physics.com/phy_demo/bernoulli-effect-equation.html
The Bernoulli Effect
The Bernoulli Equation for an
Incompressible, Steady Fluid Flow
In 1738 Daniel Bernoulli (1700-1782) formulated
the famous equation for fluid flow that bears his
name. The Bernoulli Equation is a statement derived
from conservation of energy and work-energy ideas
that come from Newton's Laws of Motion.
An important and highly useful special case is where
friction is ignored and the fluid is incompressible.
This is not as unduly restrictive as it might first
seem. The absence of friction means that the fluid
flow is steady. That is, the fluid does not stick to the
pipe sides and has no turbulence. Most common
liquids such as water are nearly incompressible,
which meets the second condition.
Consider the case of water flowing though a smooth
pipe. Such a situation is depicted in the figure
below. We will use this as our working model and
obtain Bernoulli's equation employing the
work-energy theorem and energy conservation.
1 of 4
9/11/14 4:28 AM
Bernoulli equation for incompressible, smooth fluid flow.
http://www.4physics.com/phy_demo/bernoulli-effect-equation.html
We examine a fluid section of mass m traveling to the right as shown in the schematic
above. The net work done in moving the fluid is
Eq.(1)
where F denotes a force and an x a displacement. The second term picked up its
negative sign because the force and displacement are in opposite directions.
Pressure is the force exerted over the cross-sectional area, or P = F/A. Rewriting this as
F = PA and substituting into Eq.(1) we find that
Eq.(2)
The displaced fluid volume V is the cross-sectional area A times the thickness x. This
volume remains constant for an incompressible fluid, so
Eq.(3)
Using Eq.(3) in Eq.(2) we have
2 of 4
9/11/14 4:28 AM
Bernoulli equation for incompressible, smooth fluid flow.
http://www.4physics.com/phy_demo/bernoulli-effect-equation.html
Eq.(4)
Since work has been done, there has been a change in the mechanical energy of the
fluid segment. This energy change is found with the help of the next diagram.
The energy change between the initial and final positions is given by
Eq.(5)
Here, the the kinetic energy K = mv!/2 where m is the fluid mass and v is the speed of
the fluid. The potential energy U = mgh where g is the acceleration of gravity, and h is
average fluid height.
The work-energy theorem says that the net work done is equal to the change in the
system energy. This can be written as
Eq.(6)
Substitution of Eq.(4) and Eq.(5) into Eq.(6) yields
Eq.(7)
Dividing Eq.(7) by the fluid volume, V gives us
Eq.(8)
where
Eq.(9)
3 of 4
9/11/14 4:28 AM
Bernoulli equation for incompressible, smooth fluid flow.
http://www.4physics.com/phy_demo/bernoulli-effect-equation.html
is the fluid mass density. To complete our derivation, we reorganize Eq.(8).
Eq.(10)
Finally, note that Eq.(10) is true for any two positions. Therefore,
Eq.(11)
Equation (11) is commonly referred to as Bernoulli's equation. Keep in mind that this
expression was restricted to incompressible fluids and smooth fluid flows.
2003-2008, 4Physics
Shop for neat science stuff!
Search
4 of 4
9/11/14 4:28 AM
Você também pode gostar
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeNo EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeNota: 4 de 5 estrelas4/5 (5794)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreNo EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreNota: 4 de 5 estrelas4/5 (1090)
- Never Split the Difference: Negotiating As If Your Life Depended On ItNo EverandNever Split the Difference: Negotiating As If Your Life Depended On ItNota: 4.5 de 5 estrelas4.5/5 (838)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceNo EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceNota: 4 de 5 estrelas4/5 (890)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureNo EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureNota: 4.5 de 5 estrelas4.5/5 (474)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersNo EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersNota: 4.5 de 5 estrelas4.5/5 (344)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)No EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Nota: 4.5 de 5 estrelas4.5/5 (119)
- The Emperor of All Maladies: A Biography of CancerNo EverandThe Emperor of All Maladies: A Biography of CancerNota: 4.5 de 5 estrelas4.5/5 (271)
- The Little Book of Hygge: Danish Secrets to Happy LivingNo EverandThe Little Book of Hygge: Danish Secrets to Happy LivingNota: 3.5 de 5 estrelas3.5/5 (399)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyNo EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyNota: 3.5 de 5 estrelas3.5/5 (2219)
- The Yellow House: A Memoir (2019 National Book Award Winner)No EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Nota: 4 de 5 estrelas4/5 (98)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaNo EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaNota: 4.5 de 5 estrelas4.5/5 (265)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryNo EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryNota: 3.5 de 5 estrelas3.5/5 (231)
- Team of Rivals: The Political Genius of Abraham LincolnNo EverandTeam of Rivals: The Political Genius of Abraham LincolnNota: 4.5 de 5 estrelas4.5/5 (234)
- The Unwinding: An Inner History of the New AmericaNo EverandThe Unwinding: An Inner History of the New AmericaNota: 4 de 5 estrelas4/5 (45)
- Hmel GGSRP Bathinda 16/43: Piping Material Specification 6922-6-44-0005 Rev. 0Documento81 páginasHmel GGSRP Bathinda 16/43: Piping Material Specification 6922-6-44-0005 Rev. 0Krunal Shaj100% (1)
- Fluid Mechanics Multiple Choice QuestionsDocumento10 páginasFluid Mechanics Multiple Choice QuestionsCgpscAspirantAinda não há avaliações
- Daniel Nitrogen Loaded Valve (CV7NL) - DatasheetDocumento16 páginasDaniel Nitrogen Loaded Valve (CV7NL) - DatasheetMarcelo PinheiroAinda não há avaliações
- Venturimeter and Orifice MeterDocumento5 páginasVenturimeter and Orifice MeterVrushiket Patil100% (1)
- USM Process Heat Transfer ExamDocumento11 páginasUSM Process Heat Transfer ExamSaiful MunirAinda não há avaliações
- Universiti Tun Hussein Onn Malaysia: ConfidentialDocumento3 páginasUniversiti Tun Hussein Onn Malaysia: ConfidentialIrfan FadzailahAinda não há avaliações
- Sizing of Relief Valves (Critical and Two-Phase Flow) With Isentropic Nozzle Model (HEM)Documento2 páginasSizing of Relief Valves (Critical and Two-Phase Flow) With Isentropic Nozzle Model (HEM)Nadia BahloulAinda não há avaliações
- Commissioning the S-Series TurbineDocumento1 páginaCommissioning the S-Series TurbineVilas m ChinkeAinda não há avaliações
- Yoshitake SF-1S 1F Sight GlassDocumento1 páginaYoshitake SF-1S 1F Sight GlassJohn Marvin ValenzuelaAinda não há avaliações
- PumpsDocumento24 páginasPumpsDeva RajAinda não há avaliações
- FM Merge PDFDocumento80 páginasFM Merge PDFSushant PatilAinda não há avaliações
- Week 04 MS2220 Basic Fluid Mechanics CH 31 To 38 Fluid DynamicsDocumento99 páginasWeek 04 MS2220 Basic Fluid Mechanics CH 31 To 38 Fluid DynamicsJessy PatriciaAinda não há avaliações
- Job No.: Client: Project: Region:: Sl. No. EIL Ref. No. PO No. PO DescriptionDocumento6 páginasJob No.: Client: Project: Region:: Sl. No. EIL Ref. No. PO No. PO DescriptionSuyog GawandeAinda não há avaliações
- 19-31 Ariyanto, Tati NoviatiDocumento13 páginas19-31 Ariyanto, Tati Noviatibimokananda2019Ainda não há avaliações
- SWAT Modeling Runoff in Complex CatchmentsDocumento26 páginasSWAT Modeling Runoff in Complex CatchmentsalzyoudAinda não há avaliações
- Assignment 009Documento6 páginasAssignment 009KahledAinda não há avaliações
- Jadual Peratusan Masa C02 6.8Documento6 páginasJadual Peratusan Masa C02 6.8Cucu MaAtok MeseiryAinda não há avaliações
- Physics - 4. FluidDocumento28 páginasPhysics - 4. FluidPUSHKAR KUMARAinda não há avaliações
- Domestic Oil Tanks - 2500 LitreDocumento2 páginasDomestic Oil Tanks - 2500 LitreTitanEnvAinda não há avaliações
- Reference Reach Reference Reach: The Spreadsheet The SpreadsheetDocumento7 páginasReference Reach Reference Reach: The Spreadsheet The SpreadsheetJulio Carrion ContrerasAinda não há avaliações
- Assignment Water Supply (Individual)Documento24 páginasAssignment Water Supply (Individual)eryky21Ainda não há avaliações
- Alishba ShahidDocumento9 páginasAlishba Shahidalishbashahid0611Ainda não há avaliações
- Rapidly Varied Flow Examples and Channel ControlsDocumento17 páginasRapidly Varied Flow Examples and Channel ControlsNahom GebremariamAinda não há avaliações
- Blood Pressure ChartDocumento4 páginasBlood Pressure ChartSaleem KhanAinda não há avaliações
- Steady Flow, Otherwise It Is Called As Unsteady Flow.: Prof. Dr. Atıl BULUDocumento59 páginasSteady Flow, Otherwise It Is Called As Unsteady Flow.: Prof. Dr. Atıl BULUMigori Art DataAinda não há avaliações
- Pushing The Limits: The Pressures That Drive Hydraulic Fluids To New HeightsDocumento4 páginasPushing The Limits: The Pressures That Drive Hydraulic Fluids To New HeightsJako MishyAinda não há avaliações
- 4.5.2 Rankine Half-BodyDocumento1 página4.5.2 Rankine Half-Body224883061Ainda não há avaliações
- Complex Engineering Problem of FMDocumento9 páginasComplex Engineering Problem of FMRao MaazAinda não há avaliações
- ME320 Professor John M. Cimbala: Water Draining From A TankDocumento6 páginasME320 Professor John M. Cimbala: Water Draining From A TankShohag HossainAinda não há avaliações