Escolar Documentos
Profissional Documentos
Cultura Documentos
Elegant Connections Physics Lift Circulation PDF
Enviado por
Himanshu vermaTítulo original
Direitos autorais
Formatos disponíveis
Compartilhar este documento
Compartilhar ou incorporar documento
Você considera este documento útil?
Este conteúdo é inapropriado?
Denunciar este documentoDireitos autorais:
Formatos disponíveis
Elegant Connections Physics Lift Circulation PDF
Enviado por
Himanshu vermaDireitos autorais:
Formatos disponíveis
ELEGANT CONNECTIONS IN PHYSICS .
How Airplanes Fly:
Lift and Circulation
by Dwight E. Neuenschwander
Professor of Physics
Southern Nazarene University
Bethany, OK
where ρ denotes the fluid’s density and g the
N
o matter how much physics you know, gravitational field. Since the top and bottom
it’s still amazing to see a 380,000 lb. surfaces of a wing have essentially the same
airplane fly. Whenever I fly vertical coordinate y, it follows that Pl > Pu if and
commercially, I request a window seat. The only if vl < vu. But why should the air move
view of the landscape from on high is more faster over the top surface? Answering this
interesting than any movie. The airplane’s question introduces the closed-path line
wings are fascinating to watch too—not only for integral of velocity, the “circulation” Γ,
what you see with your eyes, but also for what
you see in your mind, thanks to physics.
Γ ≡ ∮ ∙ (2)
When an airplane flies, the pressure Pl on
the lower wing surface exceeds the pressure Pu
on the upper surface. Equivalently, the air where the closed path C is traversed counter-
rushing by the lower surface moves slower than clockwise. [1] Consider an airfoil—a wing’s
air passing over the upper surface. These cross-section—in Fig. 1. The “chord length” L
statements are equivalent thanks to Bernoulli’s denotes the distance between the airfoil’s
equation—the work-energy theorem applied to leading and trailing edges. Assuming
fluids. For any two points 1 and 2 (Fig. 1) in horizontal flow, the circulation evaluated over
non-turbulent, inviscid, incompressible, path ABCD gives Γ = (vl − vu)L < 0. Now three
irrotational flow, Bernoulli says statements— Pl > Pu, vl < vu, and Γ < 0—are
equivalent articulations of the condition
(½ ρv2 + ρgy + P )1 = (½ ρv2 + ρgy + P )2 (1) necessary for lift.
….. 1 Summer 2015 …..
ELEGANT CONNECTIONS IN PHYSICS .
boundary layer separation from the surface,
which would produce energy-consuming
turbulence.
Fig. 1. The airfoil and geometry for Eq. (1).
Under conditions where Bernoulli’s equation
holds, Γ = const. [2] This is “Kelvin’s circulation
theorem.” From Eq. (2) for a fixed closed path Fig. 2. Boundary layer due to viscosity.
we have
Returning to the puzzle, a simple
∮ ∙ . (3) demonstration illustrates the crucial point. [4]
Insert a ruler, held vertically, into a pan of still
water. Suddenly push the ruler horizontally,
Consider a parcel of air of volume dV = Ady. Its
such that its chord makes a non-zero “angle of
weight dm g = ρgAdy and the pressure force
attack” with the direction of motion. Watch the
[P(y) – P(y+dy)]A turn dF = dma into
water at the trailing edge. Thanks to viscosity,
P a counter-clockwise vortex forms there (Fig. 3).
̂ g . (4)
ρ [5]
Eq. (4) shows the integral of Eq. (3) to be path-
independent, proving the theorem. But this
raises a puzzle. An airplane sitting in still air
before takeoff has Γ = 0 for any closed path
about an airfoil, but in flight Γ < 0. However,
nonzero viscosity provides the loophole that lets Fig. 3. The starting vortex.
planes fly while respecting Kelvin’s theorem.
Inviscid fluids are idealizations—zero Return to the airplane before takeoff, and
viscosity fluids would be infinitely runny. consider the closed path ABHCDKA around the
Water has a small viscosity, molasses a large airfoil (Fig. 4). This path lies outside the
viscosity. With viscosity, adjacent layers of boundary layer, where the effects of viscosity
fluid exert frictional forces on one another, are negligible, so Kelvin’s theorem applies.
tangent to the flow. On the wing surface the Before takeoff, ΓABHCDKA = 0. When the plane
velocity is zero (driving your car does not sweep accelerates forward, the counter-clockwise
dust off it), and within a few millimeters above vortex forms at the wing’s trailing edge, within
the surface the velocity reaches its free-stream closed path HCDKH, so that ΓHCDKH > 0.
value (Fig. 2). This region of velocity gradient is Consider path ABHKA that surrounds the
the “boundary layer.” [3] Aircraft fuselages and airfoil but excludes the starting vortex (Figs. 4
wings taper to pointed trailing edges to prevent and 5). Since ΓABHCDKA = ΓABHKA + ΓHCDKH (section
….. 2 Summer 2015 …..
ELEGANT CONNECTIONS IN PHYSICS .
HK in ΓABHKA cancels KH in ΓHCDKH), Kelvin’s Before encountering the wing, the parcel
theorem requires ΓABHKA < 0. With the flows approaches it with horizontal velocity v∞.
along ABHKA parallel to the chord, this Compute Δpy/Δt, which equals the net vertical
requires vl < vu. By Bernoulli’s equation this force the wing exerts on the air parcel, which is
requires Pl > Pu, and the plane flies. opposite the upward force the air exerts on the
wing. We have Δpy/Δt = (Δm/Δt) vy where Δm =
ρwhΔx for a parcel having height h, width w, and
horizontal length Δx = v∞ Δt. Thus Δpy/Δt =
ρhwv∞vy, and the upward force exerted on the
wing by the air is −ρhwv∞vy which is > 0 because
vy < 0. A vertical section of the closed path that
includes vy contributes hvy < 0 to Γ. Thus the
lifting force/length is Fy/w = −ρv∞Γ > 0.
Fig. 4. The paths used in evaluating the circulation In 1902 Martin Kutta in Germany published
around an airfoil.
“Lifting forces in flowing fluids,” which related
lift to circulation for 2-D flow past a circular
arc with a trailing edge. In 1906 Nikolai
Joukowski in Russia generalized the lift
theorem, now called the “Kutta-Joukowski lift
theorem,” [7] relating circulation to the lift,
perpendicular to v∞, for any two-dimensional
airfoil: Lift/w = −ρv∞ Γ. The value of Γ depends on
the airfoil shape. A supplementary ad hoc
Kutta-Joukowski hypothesis proposed a
steady-flow value for Γ and thus a lift that
agrees beautifully with phenomenology. [8]
Specifically, for a thin symmetrical airfoil with a
Fig. 5. The circulation path ABHKA.
curved leading edge, sharp trailing edge, chord
From another perspective, a wing gets lift length L and angle of attack θ, the K-J
because it deflects the air’s momentum hypothesis puts Γ = −πv∞ Lsinθ, so that Lift/w =
downward (Fig. 6). Consider a parcel of air +πρ(v∞)2Lsinθ. This result is to classical airfoil
bouncing off a wing with nonzero angle of design what simple pendulums and Kepler’s
attack. [6] elliptical orbits are to other areas of mechanics:
a model that serves as an excellent
approximation to reality, and a starting-point
for extensions to more complex situations. The
K-J hypothesis works for θ less than 8 to 20
degrees depending on airfoil shape; at higher
angles boundary layer separation on the upper
surface causes a stall. [9]
On December 17, 1903, the Wright brothers
achieved the first successful powered flight.
They did not use the lift theorem, but took an
empirical hands-on approach. Their airfoil
designs were guided by data they collected from
their wind tunnel. In 1909 Wilbur Wright
Fig. 6. Wing with flaps down deflecting the air’s wrote, “…I think it will save me much time if I
momentum.
….. 3 Summer 2015 …..
ELEGANT CONNECTIONS IN PHYSICS .
follow my usual plan and let the truth make means the curl is everywhere locally zero, even
itself apparent in actual practice.” [10] The though there may be large-scale circulation.
Kutta-Jukowski hypothesis for Γ, along with [2] D.J. Acheson, Elementary Fluid Dynamics
their namesake lift theorem, affirms (Clarendon Press, Oxford, UK, 1990), 157-157
theoretically what the Wrights found offers a proof in three dimensions.
experimentally. [3] ibid., 26-28.
The next time you fly commercially, ask for [4] ibid., 1-2, for a more sophisticated version of
a window seat, and really look at the wing. this table-top demonstration.
Imagine the circulation around the airfoil [5] If your ruler has a sharp leading edge, a
generating the pressure differential that keeps vortex forms there too. A leading vortex does
the airliner aloft. In humid weather this not occur for airfoils with rounded leading
circulation is sometimes made visible to the edges.
eyes (Fig. 7) as well as to the mind—because [6] Flaps and curvature of the wing surfaces
the wing has finite length, this circulation can produce the momentum transfer even with zero
show up as vortex of water vapor spinning off angle of attack.
the wing-tips. [11] Bon voyage! [7] Acheson, ref. 2, Ch. 4.
[8] ibid., 20-21. The K-J hypothesis is ad hoc
but not arbitrary, motivated by considering 2-D
flow past a cylinder, whose velocity field can be
found exactly from the Navier-Stokes equation
(F = ma applied to a viscous fluid). One then
carries out a conformal transformation to
distort the cylinder into an airfoil with a sharp
trailing edge, and the velocity field is
transformed too. The K-J hypothesis ensures a
negative Γ without the velocity becoming
infinite at the trailing edge.
[9] ibid., 29-30.
[10] ibid., 121.
Fig. 7. Humidity making the flow visible. The
condensation above the wing shows the pressure to be [11] ibid., 22-23. Vortices trailing off the
lower there. wingtips can be seen when the air is humid
and the pressure change causes condensation,
giving a rope-like vortex spinning off the
Acknowledgments wingtip. Mathematically these occur because,
by Stokes’ theorem, Γ can be written as the flux
[1] Familiar closed-path integrals include those of the curl of v through any surface that has
of force (work ) and electric and magnetic fields closed path C for its boundary. That surface
(Faraday and Amperé laws). One may wonder can go around the wingtip like a butterfly net,
how a velocity field can be “irrotational” and and vorticity must pass through that surface.
have non-zero circulation. By Stokes’ theorem,
Γ equals the flux of the curl of v. “Irrotational” All photos courtesy of the author.
….. 4 Summer 2015 …..
Você também pode gostar
- Section 2 NotesDocumento50 páginasSection 2 NotesRbe Batu HanAinda não há avaliações
- 101 Paper RoughdraftDocumento5 páginas101 Paper RoughdraftWeiyu TongAinda não há avaliações
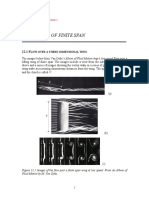
- Wings of Finite Span CantwellDocumento62 páginasWings of Finite Span CantwelljoereisAinda não há avaliações
- AA200 CH 12 Wings of Finite Span CantwellDocumento62 páginasAA200 CH 12 Wings of Finite Span CantwellMuthyala AkhilAinda não há avaliações
- AirofoilDocumento12 páginasAirofoilPrapthi gpAinda não há avaliações
- Fluids - Lecture 1 Notes: Formation of Lifting FlowDocumento78 páginasFluids - Lecture 1 Notes: Formation of Lifting FlowjavierzmorAinda não há avaliações
- Boom AeroDocumento55 páginasBoom Aeromihaly hegedusAinda não há avaliações
- Vena Contracta: Joseph Henry Laboratories, Princeton University, Princeton, NJ 08544Documento6 páginasVena Contracta: Joseph Henry Laboratories, Princeton University, Princeton, NJ 08544aiur111Ainda não há avaliações
- Cliff - Aerofoils and Wings DragDocumento9 páginasCliff - Aerofoils and Wings DragTimothy JimAinda não há avaliações
- Chapter 5 - IncompressibleFlowOver - FiniteWingDocumento18 páginasChapter 5 - IncompressibleFlowOver - FiniteWingChristian NobertoAinda não há avaliações
- Vorticity and CirculationDocumento5 páginasVorticity and CirculationChandana KarumanchiAinda não há avaliações
- Effects of WindDocumento2 páginasEffects of WindKarthikeya SrivathsavAinda não há avaliações
- Flight Without BernoulliDocumento13 páginasFlight Without BernoulliTaekevAinda não há avaliações
- VorticityDocumento5 páginasVorticitysamik4uAinda não há avaliações
- Airfoil: The Oshkosh Airfoil ProgramDocumento4 páginasAirfoil: The Oshkosh Airfoil ProgramFernando VazquezAinda não há avaliações
- Lifting Line TheoryDocumento14 páginasLifting Line Theoryhmalikn758150% (2)
- The Effect of Variable WingspanDocumento26 páginasThe Effect of Variable WingspanUriel CasiqueAinda não há avaliações
- Soil Mechanics Chapter 4Documento20 páginasSoil Mechanics Chapter 4Kc Kirsten Kimberly MalbunAinda não há avaliações
- Integral Conservation EquationsDocumento14 páginasIntegral Conservation EquationssidAinda não há avaliações
- Chap 5Documento5 páginasChap 5apratim.chatterjiAinda não há avaliações
- Fluid-Statics.: Gage Abs Atm Vac Atm AbsDocumento6 páginasFluid-Statics.: Gage Abs Atm Vac Atm AbsManu K VasudevanAinda não há avaliações
- Compressible and Finite Wing Aerodynamics: Naman BhattDocumento3 páginasCompressible and Finite Wing Aerodynamics: Naman BhattHarjaapAinda não há avaliações
- AYRS Hogg Mem Bourn 01-Oct-14Documento21 páginasAYRS Hogg Mem Bourn 01-Oct-14sbourn01Ainda não há avaliações
- Aerodynamics II - Lecture NotesDocumento17 páginasAerodynamics II - Lecture NotestherealslimAinda não há avaliações
- 11 Mechanical Properties of Fluids 2023-24.Documento33 páginas11 Mechanical Properties of Fluids 2023-24.parvezanas7Ainda não há avaliações
- Two-Dimensional Flow of Water Through Soils: Soil Mechanics-I (CENG-2202) Chapter 5: Seepage Through SoilsDocumento8 páginasTwo-Dimensional Flow of Water Through Soils: Soil Mechanics-I (CENG-2202) Chapter 5: Seepage Through SoilsbiniAinda não há avaliações
- Seepage PDFDocumento25 páginasSeepage PDFChan NovAinda não há avaliações
- AD-1key MLRITDocumento22 páginasAD-1key MLRITSaiAerrogantAinda não há avaliações
- AE 315 Lab 1: 1.1 ObjectivesDocumento18 páginasAE 315 Lab 1: 1.1 ObjectivesAngelo FonsecaAinda não há avaliações
- Vdocuments - MX - Class 11 Physics Investigatory ProjectcbseDocumento21 páginasVdocuments - MX - Class 11 Physics Investigatory ProjectcbseMiriam JomonAinda não há avaliações
- 3 Circulation Vorticity PVDocumento12 páginas3 Circulation Vorticity PVNura GuyoAinda não há avaliações
- Airflow TheoryDocumento7 páginasAirflow TheoryJoashAinda não há avaliações
- Fluid MechanicsDocumento11 páginasFluid Mechanicsjhc1123Ainda não há avaliações
- Theory of SeakeepingDocumento59 páginasTheory of Seakeepingjack white100% (2)
- Race Car AerodynamicsDocumento20 páginasRace Car AerodynamicsKrishna TejaAinda não há avaliações
- 4.9 The Joukowski Mapping: Circles To EllipsesDocumento11 páginas4.9 The Joukowski Mapping: Circles To Ellipseszero lift100% (2)
- Answer Key: B.E/B.Tech Degree Examinations: NOV/DEC-2019Documento13 páginasAnswer Key: B.E/B.Tech Degree Examinations: NOV/DEC-2019Vijayan SnAinda não há avaliações
- Physics Investigatory Project BernoullisDocumento20 páginasPhysics Investigatory Project Bernoullissamarthpanda18Ainda não há avaliações
- Gravity Waves On Water: Department of Physics, University of MarylandDocumento8 páginasGravity Waves On Water: Department of Physics, University of MarylandMainak DuttaAinda não há avaliações
- Lecture 23 - Buoyancy, Fluids in MotionDocumento4 páginasLecture 23 - Buoyancy, Fluids in MotionMol MolAinda não há avaliações
- Kutta-Joukowski Theorem: Lift Force FormulaDocumento5 páginasKutta-Joukowski Theorem: Lift Force FormulaHare krishan jhaAinda não há avaliações
- Model aeroplanes: The building of model monoplanes, biplanes, etc., together with a chapter on building a model airshipNo EverandModel aeroplanes: The building of model monoplanes, biplanes, etc., together with a chapter on building a model airshipAinda não há avaliações
- Lesher 1940Documento3 páginasLesher 1940Manabendra M DeAinda não há avaliações
- Physics Bernoulis Theorem Project CBSE Class 12Documento21 páginasPhysics Bernoulis Theorem Project CBSE Class 12Faaiz100% (3)
- Maheshwari Public School (Jawahar Nagar)Documento21 páginasMaheshwari Public School (Jawahar Nagar)Rajesh Kumar GuptaAinda não há avaliações
- Flow Past Immersed BodiesDocumento5 páginasFlow Past Immersed BodiesVijaykumar Nagathan100% (1)
- Lift-Vortex Theory PDFDocumento25 páginasLift-Vortex Theory PDFyticnisAinda não há avaliações
- Prandtl MixingDocumento4 páginasPrandtl MixingTomble BravoAinda não há avaliações
- Unit 2: Two Dimensional Inviscid, Incompressible Flow 2 Marks Question and Answers Aerodynamics 1Documento8 páginasUnit 2: Two Dimensional Inviscid, Incompressible Flow 2 Marks Question and Answers Aerodynamics 1sasiaeroAinda não há avaliações
- BarotropicDocumento3 páginasBarotropicghufron mubarokAinda não há avaliações
- Vorticity and CirculationDocumento18 páginasVorticity and CirculationShweta NagpalAinda não há avaliações
- Sistem Mekanika Hewan 2Documento23 páginasSistem Mekanika Hewan 2meet loversAinda não há avaliações
- Ananthu ProjectDocumento25 páginasAnanthu ProjectbijuAinda não há avaliações
- MODULE 5.6 OrificeDocumento19 páginasMODULE 5.6 OrificeFrancis HernandezAinda não há avaliações
- The Mechanics of Water-Wheels - A Guide to the Physics at Work in Water-Wheels with a Horizontal AxisNo EverandThe Mechanics of Water-Wheels - A Guide to the Physics at Work in Water-Wheels with a Horizontal AxisAinda não há avaliações
- C*-Algebra Extensions and K-Homology. (AM-95), Volume 95No EverandC*-Algebra Extensions and K-Homology. (AM-95), Volume 95Ainda não há avaliações
- Aviation - Theorico-Practical text-book for studentsNo EverandAviation - Theorico-Practical text-book for studentsAinda não há avaliações
- The Equidistribution Theory of Holomorphic Curves. (AM-64), Volume 64No EverandThe Equidistribution Theory of Holomorphic Curves. (AM-64), Volume 64Ainda não há avaliações
- Chemistry 1A03 Introductory Chemistry I: Unit 3 Atomic Structure & TheoryDocumento57 páginasChemistry 1A03 Introductory Chemistry I: Unit 3 Atomic Structure & TheoryRob SmithAinda não há avaliações
- Peperiksaan Percubaan SPM 2004Documento29 páginasPeperiksaan Percubaan SPM 2004Carolyn Chang Boon ChuiAinda não há avaliações
- HPSC AP Physics 2016Documento27 páginasHPSC AP Physics 2016SAHIN InspireAinda não há avaliações
- Unit Ii. Nuclear Chemistry Learning Objectives: at The End of This Chapter, The Student Will Be Able ToDocumento11 páginasUnit Ii. Nuclear Chemistry Learning Objectives: at The End of This Chapter, The Student Will Be Able ToIvyy Joyce BuanAinda não há avaliações
- SCORE300 - Phase II Test Series 2024 - T02 (Code A) - QuestionDocumento13 páginasSCORE300 - Phase II Test Series 2024 - T02 (Code A) - Questionudhav malpaniAinda não há avaliações
- Assignment 2Documento3 páginasAssignment 2Manu K Vasudevan0% (1)
- Buckling Lengths of Columns Rigorous ApproachDocumento8 páginasBuckling Lengths of Columns Rigorous ApproachBobaru MariusAinda não há avaliações
- Physics 2019 1st TermDocumento3 páginasPhysics 2019 1st TermsulayajannyAinda não há avaliações
- MIT8 01SC Problems11 SolnDocumento13 páginasMIT8 01SC Problems11 Solnडॉ. कनिष्क शर्माAinda não há avaliações
- Chlorodifluoromethane (R22), CHClF2, Physical Properties, Safety, MSDS, Enthalpy, Material Compatibility, Gas Liquid Equilibrium, Density, Viscosity, Flammability, Transport PropertiesDocumento4 páginasChlorodifluoromethane (R22), CHClF2, Physical Properties, Safety, MSDS, Enthalpy, Material Compatibility, Gas Liquid Equilibrium, Density, Viscosity, Flammability, Transport PropertiesRavi VikneshAinda não há avaliações
- Unity Secondary School Physics Chapter 21: Electromagnetism AnswersDocumento5 páginasUnity Secondary School Physics Chapter 21: Electromagnetism AnswersFrancis Ho HoAinda não há avaliações
- CSWIP Sample QuestionsDocumento31 páginasCSWIP Sample QuestionsNeo80% (5)
- PHY 101 Chapter 10 PostDocumento33 páginasPHY 101 Chapter 10 PostkjneroAinda não há avaliações
- Chemical Bonding and Molecular Structure - Recommended MCQsDocumento23 páginasChemical Bonding and Molecular Structure - Recommended MCQsAvijeet NaiyaAinda não há avaliações
- Residual StressesDocumento30 páginasResidual StressesFarhan AbbasAinda não há avaliações
- DC To DC Mobile Charging Using DDocumento12 páginasDC To DC Mobile Charging Using DanmolAinda não há avaliações
- Effects of Moisture Content On The Foundry Properties of Yola Natural SandDocumento12 páginasEffects of Moisture Content On The Foundry Properties of Yola Natural SandatikAinda não há avaliações
- Answer Key Chapter 7Documento4 páginasAnswer Key Chapter 7linAinda não há avaliações
- Mole Concept BOUNCEBACKDocumento154 páginasMole Concept BOUNCEBACKabhinav kota100% (2)
- Power Systems Unit 5Documento29 páginasPower Systems Unit 5Prathap VuyyuruAinda não há avaliações
- Secondary Test Physics DynamicsDocumento5 páginasSecondary Test Physics DynamicsApril NgAinda não há avaliações
- Numerical Analysis and Simulation of PlasticityDocumento317 páginasNumerical Analysis and Simulation of Plasticitysrikanthrajaram18100% (1)
- Vehicle TechnologiesDocumento16 páginasVehicle TechnologiesAhmet YaylıAinda não há avaliações
- 1463486214physical ChemistryDocumento4 páginas1463486214physical ChemistryShilp ShahAinda não há avaliações
- Phan Mem FBDocumento919 páginasPhan Mem FBAnonymous DNb6yWERfBAinda não há avaliações
- Intramolecular Forces and Intermolecular ForcesDocumento12 páginasIntramolecular Forces and Intermolecular ForcesDuyen Nguyen100% (1)
- Potential and Kinetic EnergyDocumento27 páginasPotential and Kinetic EnergyCza VerwinAinda não há avaliações
- Calculating Truss ForcesDocumento29 páginasCalculating Truss Forcesrecep1Ainda não há avaliações
- Solubility of Oxalic, Malonic, Succinic, Adipic, Maleic, Malic, Citric, and Tartaric Acids in Water - Alexander Apelblat & Emanuel ManzurolaDocumento4 páginasSolubility of Oxalic, Malonic, Succinic, Adipic, Maleic, Malic, Citric, and Tartaric Acids in Water - Alexander Apelblat & Emanuel ManzurolaGerardoEstebanRodríguezAinda não há avaliações
- Chemistry Form 5 (Soaps)Documento7 páginasChemistry Form 5 (Soaps)emir906Ainda não há avaliações