Escolar Documentos
Profissional Documentos
Cultura Documentos
Thermodynamics Compiled Vinodkallur
Enviado por
ravindrababugDescrição original:
Direitos autorais
Formatos disponíveis
Compartilhar este documento
Compartilhar ou incorporar documento
Você considera este documento útil?
Este conteúdo é inapropriado?
Denunciar este documentoDireitos autorais:
Formatos disponíveis
Thermodynamics Compiled Vinodkallur
Enviado por
ravindrababugDireitos autorais:
Formatos disponíveis
e-Notes by Prof.
Vinod Kalloru, RVCE, Bangalore
Thermodynamics
Basic Concepts
Session 1
Introduction:
Thermodynamics deals with heat inter-action and work inter-action with the
substances called systems. Work and heat are forms of energy. Transfer of heat or work
to a substance brings about certain changes in the substance and whatever change
happens is called a process. Thermo means heat. Since work is also a form of energy,
thermo is taken to mean heat and work. Dynamics refers to the changes that occur as a
result of heat or work transfer.
Biological systems are capable doing work. For example, micro-organism is
capable swimming in the body fluid of its host. It needs to do the work. Where does
energy for doing this work come from? It is the metabolic activity that converts some
form of energy (Nutrition that it takes form host is a form of chemical energy) into work.
It is important then to understand how this happens so that we can exploit this to our
engineering benefit.
In thermodynamics we have work transfer, heat transfer and then we have a
system for interaction which undergoes a process. Let us look at these basic terms.
System:
We need to fix our focus of attention in order to understand heat and work
interaction. The body or assemblage or the space on which our attention is focused is
called system. The system may be having real or imaginary boundaries across which the
interaction occurs. The boundary may be rigid and sometimes take different shapes at
different times. If the system has imaginary boundary then we must properly formulate
the idea of system in our mind.
1
Surroundings:
Every thing else apart from system constitutes surroundings. The idea of
surroundings gets formulated the moment we define system. System and surroundings
together form what is known as universe.
Closed system:
If the system has a boundary through which mass or material cannot be
transferred, but only energy can be transferred is called closed system. In an actual
system, there may not be energy transfer. What is essential for the system to be closed is
the inability of the boundary to transfer mass only.
Open system:
If the system has a boundary through which both energy and mass can transfer,
then it is called open system.
Properties:
Variables such as pressure, temperature, volume and mass are properties. A
system will have a single set of all these values.
Intensive properties:
The properties that are independent of amount contained in the system are called
extensive properties. For example, take temperature. We can have a substance with
varying amount but still same temperature. Density is another example of intensive
property because density of water is same no matter how much is the water. Other
intensive properties are pressure, viscosity, surface tension.
2
Extensive properties:
The properties that depend upon amount contained in the system are called
extensive properties. Mass depends upon how much substance a system has in it therefore
mass is an extensive property.
State:
It is defined as condition of a system in which there are one set of values for all its
properties. The properties that define the state of a system are called state variables.
There is certain minimum number of intensive properties that requires to be specified in
order to define the state of a system and this number is uniquely related to the kind of
system. This relation is phase rule which we shall discuss little later.
Process:
The changes that occur in the system in moving the system from one state to the other is
called a process. During a process the values of some or all state variables change. The
process may be accompanied by heat or work interaction with the system.
Heat:
It is a form of energy that exists only in transit. This transit occurs between two points
which differ in temperature. Since it exists only in transit, it should be accompanied by
changes that occur in the system. The moment this energy cease to move, it appears as
internal energy. We shall discuss internal energy when we deal with I law of
thermodynamics.
Work:
It is also a form energy that exists only in transit. The work cannot be stored. Work is
defined as the product of force and distance through the force moves. Mathematically,
3
where f is the force and d the displacement. Work is a scalar quantity.
Let us look at the following piston and cylinder arrangement containing some gas. The
system considered is the gas in the cylinder. It is exerting some pressure on the piston in
the upward direction. This is balanced by the atmospheric pressure plus the weight and
therefore piston though it is free to move, does not move. If the weight is increased, then
the piston moves downwards. The pressure of the gas increases and the movement of the
piston stops when the pressures become equal. The additional weight is doing the work
on the gas. The additional weight has to push the force created by the gas inside to move
the piston. So there is force and distance. But as the piston moves, the pressure
continuously changes. Therefore consider small distance (dL) for which work done (dW)
is also small as shown in the figure which results in small volume change (dV). Then by
definition of work, we have, if A is the cross sectional area of the piston
d f W
cos d f
dL
4
Integrating between the two locations of the piston,
2
1
2 1
pdV W
This is the equation we use to determine the work. Please note that in general p cannot
be taken out of the integral sign as p may be continuously changing as above.
If we have a p vs. V curve, we can determine the integral as area under the curve.
The area under the curve a21b is the work done on the gas.
We can carry out a process differently with the same initial and final states given
by the points 1 and 2. Since it is a different process, the curve will be different. In that
case the area under the curve will also be different which means to say the work done is
different though the initial and final states are same. Thus the work depends upon the
process or path or how the state is changing. Such quantities are called path functions.
Since heat is also energy in transit as the work is, heat must also be a path function. No
matter what process, as long we have same initial and final states, it brings about the
same pressure difference. Such properties which depend only on state are called state
properties.
1
2
a b
p
V
5
dL f dW
,
_
A
V
d pA
pdV
Thermodynamics
Basic Concepts
Session 2
Equilibrium state:
A system is said to be in thermodynamic equilibrium if it satisfies the condition
for thermal equilibrium, mechanical equilibrium and also chemical equilibrium. If it is in
equilibrium, there are no changes occurring or there is no process taking place.
Thermal equilibrium:
There should not be any temperature difference between different regions or
locations within the system. If there are, then there is no way a process of heat transfer
does not take place. Uniformity of temperature throughout the system is the requirement
for a system to be in thermal equilibrium.
Surroundings and the system may be at different temperatures and still system
may be in thermal equilibrium.
Mechanical equilibrium:
There should not be any pressure difference between different regions or locations
within the system. If there are, then there is no way a process of work transfer does not
take place. Uniformity of pressure throughout the system is the requirement for a system
to be in mechanical equilibrium.
Surroundings and the system may be at pressures and still system may be in
mechanical equilibrium.
6
Chemical equilibrium:
There should not be any chemical reaction taking place anywhere in the system,
then it is said to be in chemical equilibrium. Uniformity of chemical potential throughout
the system is the requirement for a system to be in chemical equilibrium.
Surroundings and the system may have different chemical potential and still
system may be in chemical equilibrium.
Thermodynamic process:
A system in thermodynamic equilibrium is disturbed by imposing some driving
force; it undergoes changes to attain a state of new equilibrium. Whatever is happening to
the system between these two equilibrium state is called a process. It may be represented
by a path which is the locus all the states in between on a p-V diagram as shown in the
figure below.
For a system of gas in piston and cylinder arrangement which is in equilibrium, altering
pressure on the piston may be driving force which triggers a process shown above in
which the volume decreases and pressure increases. This happens until the increasing
p
V
1
2
7
pressure of the gas equalizes that of the surroundings. If we locate the values of all
intermediate states, we get the path on a p-V diagram.
Phase rule:
The two gas samples below have the same density, viscosity and all other intensive
properties.
1 m3 of nitrogen at a pressure of 2 atmosphere and 300 K
2 m3 of nitrogen at a pressure of 2 atmosphere and 300 K
If a gas behaves ideally, then
RT
p
V
n
nRT pV
If M is the molecular weight of the gas, then
RT
pM
V
nM
V
m
RT
pM
Thus the density of an ideal gas depends upon only temperature and pressure as all other
quantities are constants. Since p and T are same for the above nitrogen samples, density is
same. If we take out 1 cc of sample from any of those two, by observing only this 1 cc
sample we can never from where we took the sample. This means to say the samples are
exactly same and indistinguishable. They are said to be in the same state.
In order to define this state of nitrogen, we need only T and p. Thus we need minimum
two variables to specify the state. This number is given by Gibbs phase rule which is
given by
N F + 2
8
where
F : degrees of freedom
: Number of phases
N : Number of components
For the above example, number of phases is one; number of components is one therefore
the degrees of freedom are two. For a system containing liquid water and its vapor in
equilibrium, we get the degrees of freedom to be one.
Following is the phase diagram of water which describes in what phase or phases
it can exist for different temperature and temperature.
9
T
p
Liquid
Solid
Vapor
10
For the system to have two phases, if we mention the temperature alone given by
the vertical line, the pressure has to be the one given by horizontal line. Given the
pressure, its temperature gets fixed. Thus we have a freedom of fixing only one of them
which amounts to say degrees of freedom is one.
Heat reservoirs:
If the temperature of the system does not change if we remove a finite quantity of
heat from it, then the system is said to be heat reservoir. If the temperature of the system
does not change if we add a finite quantity of heat to it, then the system is said to be heat
sink.
Ocean can be made to act either as heat reservoir or heat sink.
Heat Engine:
Work and heat are forms of energy and are inter-convertible. Any device which
converts continuous supply of heat into useful work continuously is called heat engine.
For any system to undergo continuous process, it should be cyclic. The detailed
mathematical treatment of heat engines will follow in 5
th
chapter on second law of
thermodynamics.
Irreversible process:
If a thermodynamic process takes place in such a way that we can retrace the path
exactly, the process is called reversible. Consider a piston and cylinder arrangement with
piston free to move at some pressure and temperature in equilibrium. The pressure of the
gas is balanced by a pressure equal to sum of atmospheric pressure and the weight on the
piston pan as shown. If the weight on the piston is reduced, then the piston moves up. Let
us just displace the part of the weight horizontally. This involves work. The piston moves
up as it is free to move until the pressures again become equal.
11
Following is the p-V diagram for the process.
State -2
12
State -1
Looking at the sequencing of the events, it is
1. Removal of part of weight on the piston which takes some work.
2. Moving of piston upward following some path on p-V diagram as shown.
Reaching a new steady position called state 2.
Reversal of these events will mean
1. Piston moving downward from state-2 to state-1.
2. Weight moving on to the piston.
Can this reversal be possible? During expansion step, the system does work on the
surroundings. In reverse then, the surroundings should do the work at state 2. This is
not possible as the system and the surroundings have the same pressure. Exact reversing
is not possible. The process of bringing the weight on the piston pan is also not possible
as we need to do only by moving horizontally. The pan level is higher than that of the
weight. This requires extra work to be done. Further, in moving the weight work was
done on the weight. In reverse then, the weight should do the work, go and sit on the pan!
Clearly this is ridiculous which is not possible.
p
2
1
13
V
In order for a process to be reversible, the driving force must be infinitesimally small. If
we remove the weight bit by bit and place it horizontally, every bit would be placed one
above the other and then piston moves upward. At any point, the piston and the bit
removed are at the same level. As a result, at any point, we can move the bit horizontally,
making the piston move a bit down where the next bit of weight is available at the same
level. Reversing is thus possible.
However there is one work that can never be reversed even in this process. That is the
work done on the bit to move it horizontally. But this is less irreversible compared to the
earlier process where large part of the weight was removed. Look at the state-2, in order
to reverse; the weight has to be lifted by some vertical distance which is missing in the bit
by bit process. We can only strive to make a process only closer to reversibility.
Thermodynamics
Session 3
First law is a statement of law of conservation of energy. For a closed system,
since there is no mass exchange with the surroundings, the total energy of the system
must be always a constant. One form of energy may be converted into another. The
system may possess several forms of energy such as kinetic energy, potential energy,
internal energy.
Potential energy:
It is the energy possessed by a body by virtue of its position. An object kept at a
height z, possesses energy to do the work. A spring kept in a compressed state is also
capable of doing work. A body is said to be possessing energy only if it can lift weight by
some mechanical means. If we tie a rope to a body at higher level, pass the rope over a
pulley and tie the other end to another body whose mass is slightly lower, the second
body will be lifted. To one end of the compressed spring in the vertical position, tie a
weight and then release the spring. The weight goes up. Thus a body at higher level or
14
spring in its compressed state possesses energy. The potential energy of a body of mass
m at height of z from some arbitrary level (reference level) is given by
mgz E
P
Arbitrary level may by any level. As long as the same, the changes in energy will also be
same. The changes in potential energy as the level changes will be
z mg z z mg E
i f P
) (
Kinetic energy:
It is defined as the energy possessed by a body by virtue of its velocity. For a
body of mass m which is moving with a velocity u, the kinetic energy is given by,
2
2
1
mu E
K
Change in kinetic energy is
2 2 2
2
1
) (
2
1
u m u u m E
i f K
Internal energy:
When some external work is transferred to a body, its temperature increases
indicating rise in internal energy. Internal energy is due to molecular energy of vibration
and rotation.
First law of thermodynamics for a closed system:
15
If Q is the amount of heat transfer to a system which does W amount of work
(work transfer form the system), then the change in the total energy of the system will be
Q W. This change will have its implications on the kinetic, potential and internal
energy. Since law of conservation is to be valid, the change in internal energy Q W
must be equal to the changes occurring in all forms energy. Mathematically,
K P
E E U W Q + +
Generally, the changes in kinetic and potential energy will be negligible compared to heat
and work interaction,
U W Q
This is first law of thermodynamics. Note that Q is the heat transfer to the system and W
is work done by the system.
Cyclic process:
If the process occurs in such a way that periodically its state repeats then the
process is called cyclic process. The following p V diagram represents a cyclic process.
16
The states 1, 2 and 3 keep repeating in the process in that order. Not only this, all the
states in between also will repeat. Every time process state changes from 1 to 2, 2 to 3
and 3 to 1 following the same paths. During such processes, there will be heat and work
interaction. All the properties will get the same values at state 1 regardless of number of
times cycle repeats. Thus
0
1 3 2 1 1 3 2 1 1 3 2 1 1 3 2 1
T p V U
First law applied to a cyclic process:
Since the change in internal energy is zero,
W Q
W Q
W Q U
0
This means that net heat transfer to the system is the net work done by the system.
p
V
1
2
3
17
Cyclic process consists of several steps. In the cyclic process shown in the diagram, there
are three steps viz., 1-2, 2-3 and 3-1.
Let us have another cyclic process for which heat and work interaction are known as
below.
Step Heat interaction Work interaction
1-2 Q
1-2
is added to the system No work interaction
2-3 Q
2-3
is removed form the system W
2-3
is the work done by the system
3-1 Q
3-1
is added to the system W
3-1
is the work done on the system
Net heat transfer to the system, 1 3 3 2 2 1
+ Q Q Q Q
Net work done by the system, 1 3 3 2
W W W
and
W Q
Flow processes:
So far we considered closed systems only. Let us look at open systems. Mass
exchange can occur. If the process variables do not change with respect to time for the
system, the process is said to be under steady state conditions. Under such conditions the
mass of the system is constant. This is due to the equality of mass entering and leaving.
If the system as a whole is moving undergoing changes, it constitutes steady state flow
process only when the system at a fixed location will have fixed values.
18
This diagram shows an open and steady state flow process. The equipment considered is
between 1 and 2. The gas enters at 1 and leaves at 2. Steady state flow process requires
mass entering at 1 is equal to mass leaving at 2. If certain mass of gas considered to be
the system, such as cylindrical shaped gas at 1, when it reaches a particular location such
as A, it will be at a state (having certain fixed values for all the properties). No matter
what time, the system at A will be in the same state. This is true for all locations.
However, state of the system differs from location to location. There is no variation of the
state with respect to time at a given location.
Heat in, Q
Work output, W
s
1
2
z
1
z
2
A
19
Thermodynamics
Session 4
First law applied to flow process:
Following is the equipment through which the steam is flowing.
Steam enters at 1 and leaves at 2. There is a heat exchanger which adds heat Q to
the steam making it superheated. The superheated steam runs the turbine and shaft work
is obtained. Thus the gas does the work W
s
. The kinetic, potential and internal energy of
the gas changes as it goes from one location to the other. The entrance 1 is at height z
1
and exit is at height z
2
from some reference datum. The velocity of the gas varies as the
flow area varies along the path.
Let us consider unit mass of steam whose volume is the volume of cylinder shown
at location 1. This steam element enters the equipment, goes through it receiving heat Q
in the exchanger, doing work at the turbine and comes out at 2. There are changes
occurring in potential (as the height at which the steam element is present changes),
Heat in, Q
Work output, W
s
1
2
z
1
z
2
20
kinetic energy (as the velocity changes) and internal energy. Let u
1
and u
2
be the
velocities at location 1 and 2. Change in kinetic energy, since m =1, is
) (
2
1
2
1
2
2
u u E
K
Change in potential energy of the steam from 1 to 2 is
) (
1 2
z z mg E
P
Let the change in internal energy be . U We must account for all heat and work
interaction that occur during the process of steam element moving form 1 to 2. The heat
Q is getting transferred in the heat exchanger to the steam element. Apart from work
output of the turbine, there are other fork forms. At location 1, the surrounding has to do
the work on the steam element to push it into the equipment. If the pressure of the steam
is p
1
, and the cross sectional area of the pipe is a
1
, then the distance moved by the steam
element is V
1
/ a1 where V
1
is the specific volume of the steam at 1. The work done at the
entrance on the steam element at 1 is then,
1 1
1
1
1 1 1
) ( V p
a
V
a p W
(Work done on the system)
Similarly work needs to be done by the steam element at section 2 as it has to push the
surrounding which is given by
2 2
2
2
2 2 2
) ( V p
a
V
a p W
(Work done by the system)
The entrance and exit work are also called as flow work. The product of pressure and
volume is the flow work.
21
If the steam element gets into the equipment, it receives work done by the previous steam
element and uses it to push the element next to it. Thus the net work is zero for all the
locations inside the equipment.
Thus the net work done by the element,
1 2
W W W W
S
+
1 1 2 2
V P V P W W
S
+
Substituting in first law of thermodynamics,
) ( ) (
) (
1 1 1 2 2 2
1 1 2 2 1 2
1 1 2 2
V p U V p U E E W Q
V p V p U U E E W Q
E E V p V p W Q
U E E W Q
P K S
P K S
P K S
P K
+ + + +
+ + +
+ + +
+ +
The group
pV U +
occurs frequently in flow processes and is called enthalpy denoted
by the letter H.
pV U H +
Since internal energy, pressure and volume are state functions, enthalpy is also state
function. The above equation becomes,
H E E W Q
H H E E W Q
P K S
P K S
+ +
+ +
1 2
This equation is first law of thermodynamics applied to flow processes. If the changes in
potential and kinetic energy are very small then,
H W Q
S
Heat capacity:
Heat capacity of a substance is defined as the heat transfer necessary to bring
about a change in the temperature of unit amount of substance by one degree centigrade.
Since it is heat transfer which is a path function, it depends upon the way heating is done.
For example gases can be heated to increase the temperature by two different methods.
The unit quantity of gas taken in container with rigid wall, when heated its volume
remains constant. Another method is to have the wall which is flexible. If the piston is
movable in the piston and cylinder arrangement, gas when heated pushes piston and
22
pressure will be constant. Even if we take unit amount of gas in both these heating
methods, it is observed the heat transfer is not the same. Thus we have heat capacity and
constant volume and heat capacity at constant pressure. Mathematically,
dT
dQ
C
p
p
dT
dQ
C
V
V
dT
dQ
C
The heat capacity at constant volume will not be equal to that at constant pressure.
23
Thermodynamics
Session 5
Prepared by Vinod Kallur, RVCE, Bangalore.
PVT Behavior of fluids
Pressure, temperature and volume of gases vary in a definite manner. Based upon the
conditions, matter can exist in solid, liquid and gas phase. This is represented in graphical
form as below. This diagram is for pure water. All pure substances will have more or less
similar diagrams.
Based upon the values of pressure and temperature, if the point lies in a region, the
substance will exist in the corresponding state represented. For example the point a
represents solid state and b represents vapor state. Any point lying on the curve
represents both the phases which are in equilibrium. For example, the point d represents
liquid water and its vapor in equilibrium. Thus there are numerous pair of pressure and
temperature values on the curve and all those points represent liquid and vapor in
equilibrium. Each curve will have always two phases in equilibrium.
T
p
24
Liquid
Solid
Vapor
Critical Point.
Fluid
Gas
a b
d
p T diagram for pure water
The point where all the curves meet is called triple point and at this condition, all the
three phase exist in equilibrium. Critical point is the highest temperature and highest
pressure where the liquid and its vapor can exist in equilibrium.
For all pressures and temperatures higher than those at critical point, the liquid and vapor
properties become similar. This state is called fluid.
Phase is considered liquid if it can be vaporized by reduction in pressure keeping T
constant. This is represented by vertical downward arrow in the figure. The initial point is
in liquid phase region. Phase is considered gas if it can be condensed by reduction in T
keeping p constant. This is shown by horizontal arrow pointing towards left. The point a
represents solid state which on increasing the temperature at constant pressure, only the
temperature of the solid increases until it reaches curve where first drop of liquid appears
and beyond this only vapor exists. This is shown as arrow a b.
The other way is representation using p V diagram for pure substance which is given in
the next figure.
S / V
L / V
L S
C
p
C
p
V
S / L
V
C
T
C
Gas
V
fluid
25
p V diagram for pure substance
There are regions where two phases co-exist in equilibrium. The dashed curve labeled Tc
represents an isotherm at critical temperature.
In thermodynamics, we deal largely with either vapor or gases. The significant portion of
the diagram is given below.
26
The substance at point 1 is in liquid state. If we decrease pressure keeping temperature
constant, the volume decreases along the dashed curve. But this change is very small and
this is why liquids are considered incompressible. Volume change with pressure at
L / V
L
C
p
C
p
V
V
C
T
C
Gas
V
fluid
1
2 3
T
1
4
27
p V diagram for pure substance
constant temperature is negligible for liquids. Decreasing pressure from 1 at constant
temperature (T
1
), a point 2 will be reached where first bubble of vapor appears. Any
further attempt to decrease the pressure fails bringing pressure down, instead more and
more liquid becomes vapor and the pressure and temperature remain constant represented
by dashed horizontal line. Thus point such as 3 represent liquid and vapor in equilibrium.
Further attempt in decreasing the pressure brings the state to the point 4 where all the
liquid becomes vapor. Further decrease in pressure at constant will follow the dashed
curve in the gas region. Thus the dashed line represents an isotherm (T
1
). Given in the
figure there is one more isotherm at a temperature less than T
1
. The dumb bell shaped
curve represents the locus of all points on all isotherms where the points similar to 2 and
3 lie. The isotherms of higher temperature lie on higher and saturated liquid and vapor
volume become closer and closer and finally merge at the critical point. This is point
where liquid and vapor cannot be distinguished. Isotherm T
C
has a point of inflexion at
the critical point.
A point on the curve is called point of inflexion if there is a tangent at that point which
lies on either side of the curve as shown below.
How do we represent this complicated behavior mathematically? This is a challenge
which led to lot of research and we have several mathematical equations. All these
equations do have limitations. We will use simple mathematical equation. This is not a
limitation as no matter what equation all it does is relate pressure, temperature and
volume of gases.
Ideal gas equation: For one mol of any gas,
Internal energy is a function of temperature only.
28
RT pV
2
1
T
T
V
dT C U
2
1
T
T
P
dT C H
No matter what process, the changes in internal energy and enthalpy are given by the
above expression not only for ideal gases even for real gases.
This law is valid for low pressures, large volumes and low temperatures.
At constant pressure
At constant volume
Isochoric Process:
Any process in which volume of the system does not change is called isochoric process.
Work done is zero.
Isobaric process:
pdV dQ dU
29
, dT C dQ
dT
dQ
C
P
p
P
,
_
, dT C dQ
dT
dQ
C
V
V
V
,
_
W Q U
Q U
) (
1 2
2
1
T T C dT C U
V
T
T
V
Q T T C dT C H
P
T
T
P
) (
1 2
2
1
dT C dQ
P
) ( ) (
1 2 1 2
V V p T T C
pdV dT C dU
P
P
) (
1 2
T T C Q H
P
) (
1 2
V V p W
Relation between heat capacities:
Isothermal Process:
Since the temperature is constant there will not be any change in internal energy.
RdT dU dH
RT U H
PV U H
+
+
+
RdT dT C dT C
V P
+
R C C
V P
+
R C C
V P
V P
C C >
30
dW dQ
dW dQ dU
2
1
1
2
ln ln
p
p
RT
V
V
RT W Q
0 U H
Adiabatic Process:
There will not any heat exchange, Q = 0.
dW dU
2
1
V
V
pdV
2
1
V
V
dV
V
RT
2
1
ln
p
p
RT
2
1
ln
p
p
RT
2
1
V
V
pdV W Q
dV
V
RT
dT C
V
dV
V
RT
dT C
V
V
dV
C
R
T
dT
V
31
2
2 2
1
1 1
T
V p
T
V p
V V
P
C
R
C
C
1
V V
P
C
R
C
C
1
1
V
C
R
The temperature and volume change according to the above equation.
The pressure, temperature and volume all vary in the adiabatic process.
Let us get a relation between the other variables.
Since the gas is ideal,
V
dV
T
dT
) 1 (
V
dV
T
dT
) 1 (
2
1
2
1
) 1 (
V
V
T
T
V
dV
T
dT
1
2
1
2
ln ) 1 ( ln
V
V
T
T
1
2
1
1
2
,
_
V
V
T
T
1
2
1
1
2
ln ln
,
_
V
V
T
T
32
2
2 2
1
1 1
T
V p
T
V p
1 1
2 2
1
2
V p
V p
T
T
1
2
1
2
1
1
2
,
_
V
V
V
V
p
p
2 2 1 1
V p V p
p T
T
V
T V
p
H
,
_
,
_
2
1
T
T
V
dT C W U
dW dU
) (
1
1 2
T T
R
1
2 2 1 1
V p V p
W
2
1
2
1
dT C U
dT C H
V
P
33
) (
1 2
T T C W
V
1
1 2
RT RT
1
1 1 2 2
V p V p
2 2 1 1
V p V p
,
_
1
2
2
1
V
V
p
p
1
2
1
1
2
,
_
p
p
V
V
1
1
1
]
1
,
_
1
2
1
1
2 1 1
1
1 p
p
p
p V p
W
1
1
1
]
1
,
_
1
1
2
1
2 1 1
1
1 p
p
p
p V p
1
1
1
]
1
,
_
1
1
1
2 1 1
1
1 p
p V p
W
( )
; 1
1
/ 1
1
2 1 1
1
1
]
1
,
_
p
p V p
W
( )
1
1
]
1
,
_
/ 1
1
2 1 1
1
1 p
p V p
U
Polytropic Process:
It is a representation of all the processes in a mathematical form as below.
Sl. No n Process
1. 0 Isobaric
2. 1 Isothermal
3.
Isochoric
Generally n lies between 1 and .
34
const pV
n
Thermodynamics
Session 6
Prepared by Vinod Kallur, RVCE, Bangalore.
Guidelines to represent processes on p V diagram:
In the figure above there are two isotherms shown. For these isotherms,
.
1 2
T T >
There
is one isotherm passing through every point on p V diagram. Higher the temperature
higher will be location of the isotherm. As they go downwards they converge as shown.
No two isotherms will ever intersect.
p
V
T
1
T
2
35
Similarly every point has an adiabatic curve passing through it. The adiabatic curve
follows the relation const pV
. Thus every point is an intersection of an isotherm and
an adiabatic curve as shown below. The adiabatic curve is steeper.
No two adiabatic curves will ever intersect.
The mathematical relation between pressure, volume and temperature applicable all
ranges of values has not been possible. However, there are equations which are valid over
certain ranges.
Conditions for any equation to be equation of state:
1. The equation should reduce to
RT pV
As p 0.
2. p-V curve should have a point of inflexion for isothermal at critical point C,
0
,
_
C
V
p
and 0
2
2
,
_
C
V
p
Van der Waals equation of state:
( ) RT b V
V
a
p
,
_
+
2
Here a and b are constants that depend upon the gas. If we apply the partial derivative
conditions, we get,
C
C
C
C
p
RT
b
p
T R
a
8
;
64
27
2 2
36
p
V
Isotherm
Adiabatic curve
The Van der Waals equation is cubic in V. Therefore it should have three roots for a
given set of values of pressure and temperature and for a given substance. For any
temperature higher than critical temperature, there is one positive root. For critical
temperature and critical pressure, all the three roots will be equal which gives critical
volume. For temperature and pressure less than critical values, there will be three roots,
least one gives the molar volume of saturated liquid and highest gives that of saturated
vapor which are volumes given by the two ends of horizontal section of the isotherm.
Redlich Kwong Equation:
T b V V
a
b V
RT
p
) ( +
Applying the partial derivative condition, we get
C
C
C
C
p
RT
b
p
T R
a
0867 . 0
;
4278 . 0
2 / 5 2
Note that the above equations reduce to the equation
, RT pV
as p 0.
Other equations of state are Peng Robinson and Virial equations.
Numerical problem:
Air is compressed from an initial state of 1 bar and 298 K to a final state of 5 bar and 298
K through two mechanically reversible processes in a closed system. First heating at
constant volume followed by cooling at constant pressure. Calculate W, Q, change in
enthalpy and internal energy. Use
2
5
,
2
7 R
C
R
C
V P
.
37
a
2
V
p
Isotherm at 298 K
The path is shown in the figure. 1 - a represents heating at constant volume and a - 2
represents cooling at constant pressure. Note that initial and final states lie on a single
isotherm.
Let us do the calculations for one mol of gas.
For the path 1 a, since volume is constant, work done is zero.
dQ dU
dT C dU
V
a
T
T
V a
dT C U
1
1
To use this we need to know temperature at a. Since it is closed system and volume is
same at 1 and a,
1 1
T p T p
a a
Since pressure at a is same as that at 2,
K
p
T p
p
T p
T
a
a
1490
1
) 298 ( 5
2
1 1 1 1
a
T
T
V a
dT C U
1
1
kJ
J
R
dT
R
775 . 24
7 . 24775
) 298 1490 (
2
) 314 . 8 ( 5
) 298 1490 (
2
5
2
5
1490
298
Thus Q
1-a
= U
1-a
= 24.775 kJ.
38
1
kJ J dT C H
P a
686 . 34 34686 ) 298 1490 (
2
) 314 . 8 ( 7
1490
298
1
You can use the formula
) ( ) (
1 1 1 1 1 1
V p V p U pV U H
a a a a a a
+ +
to calculate change in enthalpy.
For the step a 2,
dW dQ dU
2
2
T
T
V a
a
dT C U
kJ
J
R
dT
R
775 . 24
7 . 24775
) 1490 298 (
2
5
2
5
298
1490
kJ J dT C H
P a
686 . 34 34686 ) 1490 298 (
2
) 314 . 8 ( 7
298
1490
2
pdV dW
2
2
a
a
pdV W
Along the path a 2, since pressure is constant and equal to 5 bar,
2
2
a
a
pdV W
) ( 10 5
2
5
a
V V x
We should know the volume at a.
From gas law, at the initial condition,
3
5 1
02477 . 0
10 1
) 198 ( 314 . 8
m
x
V
Note that we have taken one mol.
39
1
1 1
2
2 2
T
V p
T
V p
The temperatures are equal,
2
1 1
2
p
V p
V
3
004954 . 0
5
) 02477 . 0 ( 1
m
Similarly,
3
5
1245 . 0
10 1
) 1498 ( 314 . 8
m
x p
RT
V
a
a
a
kJ J x V V p W
a a
773 . 59 59773 ) 1245 . 0 004954 . 0 ( 10 5 ) (
5
2 2
Since the volume is decreasing, work is done on the system.
kJ Q
Q
W Q U
a
a
a a a
548 . 84
) 773 . 59 ( 775 . 24
2
2
2 2 2
For the entire process,
kJ Q Q Q
a a
773 . 59 ) 548 . 84 ( 775 . 24
2 1 2 1
+ +
0 686 . 34 686 . 34
0 775 . 24 775 . 24
2 1 2 1
2 1 2 1
+
+
a a
a a
H H H
U U U
kJ W W W
a a
773 . 59 ) 773 . 59 ( 0
2 1 2 1
+ +
Since there are no changes in internal energy and enthalpy, work done on the system is
given out as heat.
40
Thermodynamics
Session 7
Determination of changes in internal energy and enthalpy:
No matter what is the process the internal energy and enthalpy are determined using the
following formulae.
dT C dH
dT C dU
P
V
If the process is isochoric, then
. dQ dT C dU
V
If the process is isobaric, then
. dQ dT C dH
P
Let us recall that
1. For ideal gases internal energy is a function of temperature only.
2. The change in internal energy is a state function.
Let us take an adiabatic process and determine change in internal energy.
41
p
V
1
2
Consider two states (1) and (2) on an adiabatic path. There is one isotherm for each state
as shown. Adiabatic curve at (1) is steeper than the isotherm. Whether the process
follows adiabatic path or another curve shown in the figure or any arbitrary path, as long
the initial and final state are same, we get the same change in internal energy.
Let us replace adiabatic path by two steps
1. 1 a constant volume process followed by
2. a 2 isothermal process
to accomplish the same change in the state.
2 1 2 1
+
a a
U U U
a
42
p
V
1
2
Since step 1 a is a constant volume process,
dT C dU
V
will have to be used. The
step a 2 is isothermal and therefore dU = 0.
0
1
2 1
+
a
T
T
V
dT C U
Since
, T T
a 2
2
1
2 1
T
T
V
dT C U
Any process between any two states can be replaced by either an isothermal process
followed by constant volume process or constant volume process followed by an
isothermal process. The total change in internal energy is the change in internal energy
for constant volume step only. Thus no matter what process the change in internal energy
is given by
dT C dU
V
.
Same idea may be extended to change in enthalpy.
Deviations of real gases form ideal behavior:
The deviation from ideal behavior is measured using what is known as
compressibility factor defined as the ratio of volume determined using ideal gas law
to the actual volume at any given temperature and pressure.
For ideal gases, Z = 1. Higher the value Z away from one higher will be the non-ideality.
Following figure gives the value of Z as a function pressure for different gases. All gases
approach ideal gas behavior at low pressures. This figure is called compressibility chart.
There will be as many curves as there are number of gases. The chart that is given here is
for one temperature. Therefore this figure becomes highly cumbersome if applied for all
gases and all temperatures.
43
RT
pV
V
V
Z
ideal
actual
Theory of corresponding states:
It states that all fluids, when compared at the same reduced temperature and reduced
pressure, will have same compressibility factor and all deviate from ideal behavior to the
same extent.
CH
4
N
2
Z
1.0
p
44
The reduced pressure and temperature are defined by
45
C
r
C
r
T
T
T
p
p
p
Here all gases with the same reduced temperature and pressure lie on the same curve.
This chart is called generalized compressibility chart. Different gases are indicated by
different points on the curve. There will be as many curves as there are temperatures.
This is less cumbersome compared to compressibility chart.
Z
p
r
0 1. T
r
5 1. T
r
5 2. T
r
46
The above table gives two gases with the same Z for different T and p. The reason is that
the critical values are different.
T p
T
c
p
c
T
r
p
r
N
2
189.
3
83.7
5
126.
2
33.
5
1.
5
2.
5
CH
4
286.0
5
114.
5
190.
7
45.
8
1.
5
2.
5
47
Thermodynamics
Session 8
Standard Heat of reaction:
It is defined as the enthalpy change accompanying a reaction when both reactants and
products are at their standard states at 298 K and is denoted by
298
0
H
.
) g ( CO ) g ( O ) s ( C 2 2
2
+
kJ . H 2 221 298
0
If the stoichiometry of the above reaction is represented as
Then,
kJ .
kJ .
H 6 110
2
2 221
298
0
Standard Heat of Combustion:
The standard heat of combustion of a substance is defined as the enthalpy change
accompanying the reaction when one mol of the substance undergoes combustion when
both reactants and products are at 298K.
The heat of combustion is 1168.12 kJ.
The standard heat of formation:
Standard heat of formation of a substance is defined as the change in enthalpy
accompanying the formation of 1 mol of the substance from the constituent elements
when the reactants and products are at 298K.
) g ( CO ) g ( O ) s ( C 2 2
2
+
kJ . H 2 221 298
0
Standard Heat of Formation of Carbon monoxide is kJ . H f 6 110
0
.
48
) g ( CO ) g ( O ) s ( C +
2
2
2
; O H ) g ( CO ) g ( O ) l ( CHO CH
2 2 2 2
2 2 2 2 + +
. kJ 222222 H 222
2
Hesss Law of constant heat summation:
The net enthalpy involved in a reaction is the same whether the reaction takes place in a
single step or in a series of steps.
C B A +
Let A and B react to form C with heat of reaction H. Let there be one more method of
carrying out this reaction in two steps as given below.
AB B A +
1
H
C AB
2
H
Treating arrow as an equal sign, adding these two reactions gives,
C B A + ,
2 1
H H +
It has been found that
2 1
H H +
is same as . H
This idea is used to determine heat of reaction from heat of formation or heat of
combustion data.
For example if we want to determine heat of formation of sulfuric acid, we must
determine this from the reaction,
No matter what we do, the above reaction cannot be carried out. Let us carry out other
possible reactions such that the over-all reaction is the formation reaction as below.
49
H
2 2 2 2
2 SO H O S H + +
2 2
SO O S +
1
H
----------(1)
3 2 2
2 2 SO O SO +
2
H
----------(2)
4 2 2 3
SO H O H SO +
3
H
-----------(3)
O H O H
2 2 2
2
1
+
4
H ----------(4)
2(1), 2(3) and 2(4) gives,
2 2
2 2 2 SO O S +
1
2 H ----------(1)
3 2 2
2 2 SO O SO +
2
H ----------(2)
4 2 2 3
2 2 2 SO H O H SO +
3
2 H
-----------(3)
O H O H
2 2 2
2 2 +
4
2 H ----------(4)
Adding these equations along with heat of reactions,
and heat of this reaction will be 2 4 3 1
2 H ) H H H ( + + +
Therefore heat of formation of sulfuric acid is
2
2
4 3 1
H
H H H + + +
This is how Hesss law can be used to determine the heat of reaction of a reaction from
heat of reaction of other reactions.
50
2 2 2 2
2 2 2 2 SO H O S H + +
Thermodynamics
Session 9
First deals with law of conservation of energy and defines internal energy.
A stone falls decreasing its potential energy and converting it into kinetic energy. Just
before it strikes the ground, it has maximum kinetic energy. From there why does it not
go up decreasing its kinetic energy and converting it into potential energy?
If we keep two bodies at different temperature in contact, why there is no heat transfer
from a body of low temperature to a body at higher temperature?
When we remove the wall which separates two gases, the two gases mix together without
any external work done on them. Why then the two gases in a mixed state separate
themselves without any external work?
For all the processes mentioned above there is absolutely no violation of I law. In spite of
that, we do not observe these processes. It appears that there is some sense of direction
for spontaneous processes. There is nothing in the first law to indicate any such direction
to any process.
Is there any difference between heat and work though they are both forms of energy? If
they inter-convertible, then any cyclic process should be able to convert all the heat
supplied into work completely as change in internal energy is zero. Does it happen? It has
been found that we cannot have a device whose sole effect is conversion of heat supplied
into work completely. Let us look at why this is so with an example of a process.
In the following figure, there is a heat exchanger where heat is supplied (Q
1
) to the
system which is water in this case and generates steam at high pressure. The steam flows
into a turbine and rotates it producing useful work W
S
. From the turbine, we get steam at
51
relatively lower pressure than with which it entered. The objective here is to convert heat
Q
1
into work. Since this heat is available, can we send the steam from turbine directly
into the heat exchanger in order to make it work continuously so that we get continuous
supply of work? This is shown by a dotted arrow.
The moment we establish this connection, whole process comes to an abrupt stop! We
have lower pressure steam line going into the heat exchanger in which there is higher
pressure steam. If there is connection like this, why does steam preferentially go into the
turbine line? It will enter into both the lines and stop the turbine. Therefore, in order to
have this going on, we must condense the steam bring about a change in its state so that it
can be fed to the heat exchanger. This state must be same as that of feed water to the heat
exchanger.
Thus there is no way Q
2
= 0. We cannot device any process which converts Q
1
completely
into work. The work obtained W
s
is less than Q
1
by an amount equal to Q
2
. By first law,
since for a cycle change in internal energy is zero,
2 1 S
Q Q W
Practically Q
2
cannot be zero.
If we analyze any cyclic process, there will be several heat and work interactions, such
that net work done is equal to net heat supplied. There will be always one step in which
Q
1
Q
2
W
S
Heat Exchanger
Condenser
Turbine
52
there is heat removed which brings down the amount of heat that is getting converted into
work.
This fact is the basis of statement of II law of thermodynamics. There are several
statements for the II law which are equivalent. In fact we can deduce one from any other.
All the statements are given below.
Second law of thermodynamics:
1. Heat cannot by itself pass from a cold to a hot body.
2. All spontaneous processes are to some extent irreversible and are
accompanied by degradation of energy.
3. It is impossible to construct a heat engine that operates continuously in a cycle
to produce no effect other than conversion of heat supplied completely into
work. This is called Kelvin Planck statement.
4. It is impossible to construct a heat pump (reverse heat engine) that operates
continuously to produce no effect other than transfer of heat from low
temperature body to a high temperature body.
Carnot cycle and Carnot engine:
The Carnot cycle consists of four steps and all the four steps are reversible. The cycle is
shown in the diagram below.
53
There are two isotherms and two adiabatic processes as shown. The isotherms are at TH
and TC.
AB Reversible isothermal expansion
BC Reversible adiabatic expansion
CD Reversible isothermal compression
DA Reversible adiabatic compression
According to first law, it can be shown that
B
A
H AB AB
p
p
ln RT W Q
) T T ( C W
C H V BC
D
C
C CD CD
p
p
ln RT W Q
) T T ( C W
H C V DA
The net work done is given by
p
V
A
B
C
D
T
H
T
C
54
DA CD BC AB net
W W W W W + + +
) T T ( C
p
p
ln RT ) T T ( C
p
p
ln RT
H C V
D
C
C C H V
B
A
H
+ + +
For adiabatic process BC,
/ ) 1 (
C
B
C
H
p
p
T
T
,
_
And for the adiabatic process DA,
/ ) 1 (
A
D
H
C
p
p
T
T
,
_
From these two,
B
A
C
D
p
p
p
p
Net work done becomes,
B
A
C H net
p
p
ln ) T T ( R W
Heat supplied with an objective of converting into work is
B
A
H AB AB
p
p
ln RT W Q
The efficiency is defined as
H
C H
B
A
H
B
A
C H
AB
net
T
T T
p
p
ln RT
p
p
ln ) T T ( R
Q
W
It is clear that efficiency of Carnot engine depends upon only the temperatures between
which it is operating and not on the working substance undergoing the cycle. Since
Carnot engine is reversible, it must have maximum efficiency.
From first law,
55
CD AB net
Q Q W
H
C
AB
CD
AB
CD AB
AB
net
T
T
1
Q
Q
1
Q
Q Q
Q
W
H
C
AB
CD
T
T
1
Q
Q
1
H
C
AB
CD
T
T
Q
Q
Let QCD is heat removed, and be equal to QC; and heat added as Q
H
, with sign convention,
H
C
H
C
T
T
Q
Q
which can be simplified to
0
T
Q
T
Q
C
C
H
H
+
This equation is applicable to the complete cycle and any quantity that adds to zero for
the cycle is a state property. Thus Q/T is a state property called entropy. Thus second law
of thermodynamics brings in the idea of entropy.
56
Thermodynamics
Session 10
Efficiency of engines:
The efficiency of reversible Carnot Engine is given by
H
C H
H
C H
T
T T
Q
Q Q
The maximum efficiency of any engine operated between two temperatures is always
given by
H
C H
T
T T
as the efficiency of a reversible engine is maximum.
Efficiency of real engine is always less than that of reversible engine. If the engine is
irreversible then efficiency is calculated from
H
C H
Q
Q Q
and not from temperatures.
For any irreversible engine,
H
C H
H
C H
T
T T
dQ
dQ dQ
<
H
C
H
C
T
T
dQ
dQ
<
H
H
C
C
T
dQ
T
dQ
<
Applying sign convention,
0
T
dQ
T
dQ
H
H
C
C
< +
57
Thus for irreversible engine,
0
T
dQ
<
If the processes are all reversible, then
0
T
dQ
In general,
0
T
dQ
This is called Clausius inequality. The sum of dQ / T terms over a cycle is less than or
equal to zero depending upon whether the cycle is irreversible or reversible.
The changes in entropy are always determined using,
58
T
dQ
dS
v Re
Let A1B Represent irreversible process and A2B represent reversible process between
the same states.
To determine entropy change we must have only reversible path. However the entropy
change between the states 1 and 2 is same regardless of the path as it is a state function.
What the above equation says is entropy is not equal to dQ/T along an irreversible path.
A
B
1
2
p
V
59
T
dQ
dS
v Re
B 2 A
B A
T
dQ
S d p
T
V
T V d T C d H
p
P
1
1
]
1
,
_
+
To determine entropy change for any irreversible path between two states, replace the
path by a reversible path with the same states, and find the entropy of the reversible path.
Entropy and irreversibility:
Let us look at a cyclic process given below.
Let A1B Represent reversible process and B2A represent irreversible process between
the same states. Therefore A2B is also irreversible. Since A1B is reversible,
B 1 A
B 1 A
T
dQ
S
Since cycle as a whole is irreversible and as per Clausius inequality,
A
B
1
2
p
V
60
0
T
dQ
T
dQ
A 2 B B 1 A
< +
RHS is independent of the path which will be equal to
B 1 A
S .
LHS is dQ / T term and it is along an irreversible path and therefore it does not represent
entropy change.
Mathematical Statement of II law:
For a process involving transfer of heat Q from heat source at T
1
to a heat sink at T
2
,
The process can be made less and less irreversible by lowering the temperature T
1
closer
and closer to T
2
.
As the temperatures become closer and closer, irreversibility decreases and
For any heat transfer there has to be some temperature difference. Therefore T
1
> T
2
and
hence,
61
2
T
dQ
<
2
T
dQ
S
A 2 B
B 2 A
< +
2
T
dQ
S
A 2 B
A 2 B
< +
A 2 B
A 2 B
S
T
dQ
<
2 2
total
T
Q
T
Q
) S ( +
,
_
2 2
2 2
total
T T
T T
Q ) S (
. 2 S
total
. 2 S
total
This is the mathematical statement of II law of thermodynamics. Thus the entropy of the
universe always increases and the energy is conserved.
Because of irreversibility, there will be some dissipation and degradation of energy which
will not be available as work. This is called lost work which is given by
total 0 lost
S T W
Where T
0
refers to the temperature of the sink to which heat is rejected.
Determination of entropy changes:
This is the basic equation. The heat transfer term may replaced by any term using first
law or any equation applicable to the process for which entropy change is to be
determined. This is applicable only the process is reversible. For example, for an ideal
gas undergoing isothermal reversible process,
pdV dW dQ
T
pdV
dS
V
RdV
dS
1
2
V
V
ln R S
This is how entropy changes may be determined
62
T
dQ
dS
R
Thermodynamics
Session 11
Fundamental Property Relations:
Apart from enthalpy, internal energy and entropy, there are other thermodynamic
properties which are necessary to apply to phase equilibria and reaction equilibria. So far
we have treated only closed systems which consist of single phase without any reaction.
In order treat the systems we need to know other energy terms involved with reaction and
phase equilibria. The use these properties will get clearer when we do the chapters on
these areas.
Let us derive the fundamental property relations from basics.
Enthalpy:
From I law,
dW dQ dU
Vdp TdS dH
Vdp pdV pdV TdS
Vdp pdV dU
d(pV) dU dH
pV U H
pdV TdS dU
+
+ +
+ +
+
+
Helmholtz free energy:
It is defined as
A = U TS
63
Differentiating,
dA = dU-d(TS)
= TdS pdV TdS SdT
dA= - pdV SdT
Gibbs Free energy:
It is defined as G = H TS
Differentiating, dG= dH TdS SdT
= TdS +Vdp TdS SdT
dG = Vdp - SdT
These four equations are called fundamental property relations as many equations are
derived from these equations.
Maxwells relations
As some of the thermodynamic properties are not directly measurable, we must write the
equations in terms of measurable properties. The measurable and determinable (by
experiment) properties are temperature, pressure, volume, heat capacities and in some
cases even enthalpies. These relations are derived from fundamental property relations.
The derivations are based upon a mathematical relation applied to exact differential
equations.
If z = f(x,y) then
dy
y
f
dx
x
f
df
x y
,
_
+
,
_
This equation is also written as
df = Mdx + Ndy
For this differential equation to be exact,
y x
x
N
y
M
,
_
,
_
64
Applying these conditions to all the property relations, we get,
Ndy Mdx df +
y x
x
N
y
M
,
_
,
_
pdV TdS dU
V S
S
p
V
T
,
_
,
_
Vdp TdS dH +
p
S
S
V
p
T
,
_
,
_
SdT pdV dA
T V
V
S
T
p
,
_
,
_
SdT Vdp dG
T p
p
S
T
V
,
_
,
_
Generating function:
Consider
2 2
T R
) RT ( Gd RTdG
RT
G
d
,
_
dT
RT
G
dG
RT
1
2
dT
RT
TS H
) SdT Vdp (
RT
1
2
,
_
RT
SdT
RT
HdT
RT
SdT
RT
Vdp
2
+
dT
RT
H
dp
RT
V
2
65
dT
RT
H
dp
RT
V
RT
G
d
2
,
_
From this equation, at constant temperature and at constant pressure we can write,
2 p
T
RT
H
T
) RT / G (
;
RT
V
p
) RT / G (
1
]
1
1
]
1
If we know G/RT in terms of p and T, it can be used to evaluate other
thermodynamic properties and hence it is called generating function.
Entropy changes:
We know that
V
V
p
P
T
Q
C ;
T
Q
C
,
_
,
_
Since
TdS dQ
,
T
C
T
S
T
S
T C
P
p
p
P
,
_
,
_
And
T
C
T
S
T
S
T C
V
V
V
V
,
_
,
_
Using these,
,
_
1
2
P
T
T
P
p
T
T
ln C
T
dT
C S
2
1
and
66
,
_
1
2
V
T
T
V
V
T
T
ln C
T
dT
C S
2
1
If S is considered as
S = f (T,p) then
dp
p
S
dT
T
S
dS
T p
,
_
+
,
_
In this equation, the first partial derivative is replaced by C
P
/T which is derived and
second by a Maxwells relation, we get,
dp
T
V
dT
T
C
dS
p
P
,
_
Similarly by taking S as function of V and T, we get,
dV
T
p
dT
T
C
dS
V
V
,
_
+
If there is any relation between three variables, from mathematics we have, a relation
between p, V and T as
1
V
T
T
p
p
V
p V T
,
_
,
_
,
_
Using these relations, we can get,
dV
) p / V (
) T / V (
dT
T
C
dS
T
p
V
dV p
) p / V (
) T / V (
T dT C dU
T
p
V 1
]
1
+
Internal energy may also be written as
1
1
]
1
+
,
_
pdV dp
T
V
T dT C dU
p
P
67
Using
, Vdp TdS dH +
we get
dp
T
V
T V dT C dH
p
P
1
1
]
1
,
_
+
68
Thermodynamics
Session 12
Internal energy changes:
The internal energy changes can be expressed in terms measurable quantities such as heat
capacities, pressure, volume and temperature. We can use Maxwells relations to get
these expressions.
The following are fundamental property relations.
We have derived the following relations.
Let us derive the expression for internal energy in terms C
P
and C
V
.
Replace dS in terms of C
V
,
dp
T
V
dT
T
C
dS
p
P
,
_
dV
T
p
dT
T
C
dS
V
V
,
_
+
dV
) p / V (
) T / V (
dT
T
C
dS
T
p
V
69
2
V
T
T
p
p
V
p V T
,
_
,
_
,
_
pdV TdS dU
pdV dV
) p / V (
) T / V (
dT
T
C
T dU
T
p
V
1
]
1
dV p
) p / V (
) T / V (
T dT C dU
T
p
V 1
]
1
+
pdV TdS dU
Vdp TdS dH +
SdT pdV dA
SdT Vdp dG
Internal energy change in terms of C
p
:
Replace dS in terms of C
p
,
Enthalpy changes:
Starting from
in the same way we can get,
We can use these expressions and find the changes in enthalpy. These equations are
applicable for any gas. P-V-T relations used should be for the gas for which you are
determining the changes.
Use these relations and derive the expressions for dH and dU for ideal gas.
Effect of p, V and T on U, H and S:
This is one of the Maxwells relations which gives the effect of pressure on entropy at
constant temperature.
This equation derived earlier gives the effect of temperature on entropy at constant
pressure.
70
pdV TdS dU
pdV dp
T
V
dT
T
C
T dU
p
P
1
1
]
1
,
_
1
1
]
1
+
,
_
pdV dp
T
V
T dT C dU
p
P
Vdp TdS dH +
dp
T
V
T V dT C dH
p
P
1
1
]
1
,
_
+
p T
T
V
p
S
,
_
,
_
T
C
T
S
P
p
,
_
At constant volume,
Or
This gives the effect of temperature on internal energy at constant volume.
At constant temperature, since dT is zero,
This gives the effect of volume of internal energy at constant temperature.
Similarly from
we can get,
At constant pressure,
At constant temperature,
These expressions give the effect of temperature and pressure on enthalpy.
Relationship between the heat capacities:
The heat capacities are related by the following expression.
which can also be written as
using the cyclic relation of partial derivatives of p, V and T.
71
dV
) p / V (
) T / V (
T Vdp dT C dU
T
p
V 1
]
1
+
V
C
dT
dU
V
V
C
T
U
,
_
1
]
1
+
,
_
p
) p / V (
) T / V (
T
V
U
T
p
T
dp
T
V
T V dT C dH
p
P
1
1
]
1
,
_
+
P
p
C
T
H
,
_
p T
T
V
T V
p
H
,
_
,
_
V p
V P
T
p
T
V
T C C
,
_
,
_
T
2
p
V P
V
p
T
V
T C C
,
_
,
_
are called Volume expansivity and isothermal Compressibility. The difference between
heat capacities is written in terms of these as
Effect of pressure and volume on heat capacities:
These are given by the following equations.
72
T
p
V
V
2
,
_
;
T
V
V
2
p
,
_
VT
C C
2
V P
p
2
2
T
P
T
V
T
p
C
,
_
,
_
2
R
V
p T
S
U
T
,
_
V
2
2
T
V
T
p
T
V
C
,
_
,
_
T
p
2
2
T
V
p
V
T
p
T
p
C
,
_
,
_
,
_
Thermodynamics
Session - 13
The equation of state of a gas
is given by
and the specific heat is given by
Derive the expressions for changes in internal energy, enthalpy and entropy for an
isobaric process.
As pressure is constant, dp = 0,
Internal energy:
Enthalpy:
Entropy:
73
2
T
c
p
RT
V
bT a C
p
+
) V V ( p ) T T (
2
b
) T T ( a U
2 2
2
2
2
2 2 2 2 2
+
pdV dT ) bT a ( dU +
pdV dT C dU
P
1
1
]
1
+
,
_
pdV dp
T
V
T dT C dU
p
P
dp
T
V
T V dT C dH
p
P
1
1
]
1
,
_
+
dT C dH
P
) T T (
2
b
) T T ( a H
2
2
2
2 2 2 2 2
+
dT
T
bT a
dS
,
_
) T T ( b
T
T
ln a S
2 2
2
2
2 2
+
dp
T
V
dT
T
C
dS
p
P
,
_
dT
T
C
dS
P
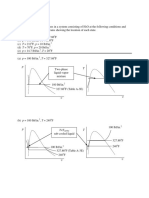
A perfect gas is heated from 60 to 300
o
C at a constant pressure of 4 bar. The gas is then
cooled to 60
o
C at constant volume. The mass of the gas is 5 kg. Determine total entropy
change. C
P
and C
V
are 1.0 and 0.72 kJ/kg.K
p
r
e
s
s
u
r
e
volume
1
1
T
2
T
2
3
74
2
2
T
T
2 2
T
dQ
S
2
2
T
T
p
T
dT C
Total entropy change = 5(0.2161)=1.0805 kJ / K
Prove that
dp ) T p ( V dT ) pV C ( dU
p
+
Where
p T
T
V
V
1
,
p
V
V
1
,
_
,
_
dp
p
U
dT
T
U
dU
T p
,
_
+
,
_
p p p
T
V
p
T
S
T
T
U
,
_
,
_
,
_
Equation (2) becomes
3
2
T
T
3 2
T
dQ
S
3
2
T
T
V
T
dT C
75
K . kg / kJ 2222 . 2
222
222
ln
222
222
ln 22 . 2 K . kg / kJ 2222 . 2
2 2 2 2 2 2
S S S
+
K . kg / kJ 2222 . 2
2222 . 2 2222 . 2 S
2 2
) p , T ( U U
pdV TdS dU
T
dQ
dS
T
dT C
dS
p
T
C
T
S p
p
,
_
p
p
p
T
V
p
T
C
T
T
U
,
_
,
_
,
_
pdV TdS dU
T p
p
S
T
V
,
_
,
_
T T T
p
V
p
p
S
T
p
U
,
_
,
_
,
_
For ideal gas show that
0
S
U
V
U
p
U
T T T
,
_
,
_
,
_
76
T p T
p
V
p
T
V
T
p
U
,
_
,
_
,
_
dp
p
V
p
T
V
T dT
T
V
p
T
C
T dU
T p p
p
1
1
]
1
,
_
,
_
+
1
1
]
1
,
_
,
_
dp
p
V
p
T
V
T dT
T
V
p C
T p p
p
1
1
]
1
,
_
+
,
_
1
1
]
1
,
_
dp ) pV V T ( dT ) pV C (
p
dp ) T p ( V dT ) pV C ( dU
p
+
pdV TdS dU
T T
S
V
p T
S
U
,
_
,
_
V T
p
T
p T
S
U
,
_
,
_
R
pV
T
R
V
p
T
V
,
_
2
R
V
p T
S
U
T
,
_
pdV TdS dU
p
V
S
T
V
U
T T
,
_
,
_
T V
V
S
T
p
,
_
,
_
p
T
p
T
V
U
V T
,
_
,
_
2 p
V
R
T
V
U
T
,
_
And hence
77
pV H U
pV U H
+
1
1
]
1
,
_
,
_
,
_
V
p
V
p
p
H
p
U
T T T
p T
T
V
T V
p
H
,
_
,
_
1
1
]
1
,
_
1
1
]
1
,
_
,
_
V
p
V
p
T
V
T V
p
U
T p T
T p T
p
V
p
T
V
T
p
U
,
_
,
_
,
_
2
p
RT
p
p
R
T
p
U
2
T
,
_
2
S
U
V
U
p
U
T T T
,
_
,
_
,
_
Thermodynamics
Session 14
Fugacity:
This is a concept used to determine Gibbs free energy for real gases. Recall that Gibbs
free energy is an important thermodynamic property used in phase and reaction
equilibria. We have one fundamental property relation,
At constant temperature,
If the gas is ideal,
Obviously this equation is not valid for real gases. To make it valid for real gases, let us
replace actual pressure by a fictitious term f, so that the equation becomes valid even for
real gases as
Here f is called fugacity and it will have the units of pressure.
Integrating,
For ideal gases,
Therefore
The fugacity is proportional to pressure.
78
SdT Vdp dG
Vdp dG
( ) p ln RTd dp
p
RT
dG
( ) p ln RTd dG
( ) f ln RTd dG
2
2
2 2
f
f
ln RT G G G
2
2
2 2
p
p
ln RT G G G
p f ., e . i
p
p
f
f
2
2
2
2
For ideal gases f = p.
As pressure is decreased, we know real gases will increasingly behave like ideal gases.
Mathematically,
Fugacity coefficient is defined as the ratio of fugacity to the pressure. The fugacity is
to be determined with reference to some standard state. The standard state is chosen such
that, the pressure is equal to fugacity. This means that, the gas is at a very low pressure.
This state is designated as f
0
corresponding to a low pressure p
0
.
Effect of temperature on fugacity:
Gibbs free energy change between any state and standard state is given by
Partial differential w. r. t. T at constant pressure,
Since f
0
is at low pressure, its variation with temperature will be negligible. Using Gibbs
Helmholtz equation,
This equation gives the effect of temperature on fugacity.
79
2
p
f
lim
2 p
2
2
f
f
ln RT G G
T
G
T
G
f
f
ln R
2
2
T
G
T
G
) f ln f (ln R
2
2
2 2
p
2
p p
2
p
T
) T / G (
T
) T / G (
T
f ln
T
f ln
R
,
_
,
_
1
1
]
1
,
_
,
_
2
2
p
RT
H H
T
f ln
,
_
Effect of temperature on fugacity:
At constant temperature,
Writing it as partial differential equation with respect to pressure at constant T,
This equation gives the effect of pressure on fugacity.
Determination of fugacity: Under isothermal condtions,
We need to integrate this between p = 0 to the pressure at which we want to determine
fugacity.
As p 0, f p , also note that
is not defined.
This can be avoided by certain simplification as below:
80
( ) f ln RTd Vdp dG
RT
V
p
f ln
T
,
_
( ) f ln RTd Vdp dG
( ) dp
p
Z
dp
RT
V
f ln d
2 p
p ln
dp
p
Z
dp
p
2
dp
p
2
+
( ) dp
p
2 Z
p ln d
+
dp
p
2 Z
p
f
ln d
,
_
( ) dp
p
Z
f ln d
( ) dp
p
2 Z
ln d
Method of residual volumes:
Residual volume is defined by
Using this in the relation,
af
Using equation of state:
81
( ) dp
p
2 Z
ln d
( )
p
2
p
2
dp
p
2 Z
ln d
p
RT
V
( ) dp
RT
V
f ln d
dp
RT
2
p
RT
,
_
+
dp
p
2
RT
,
_
+
( )
,
_
+ p ln d dp
RT
dp
RT p
f
ln d
,
_
( ) p d
RT
ln d
p
o
p
2
p d
RT
ln
p
o
( ) f ln RTd Vdp dG
( ) Vdp
RT
2
f ln d
( )
p
p
p
p
2 2
Vdp
RT
2
f ln d
p
p 2
2
Vdp
RT
2
f
f
ln
We need to apply the above result to the equation of state of your choice.
Application to Van der Waals equation:
Equation of state is
Substituting this in
We get,
Consider the integral,
Put
82
p
p 2
2
Vdp
RT
2
f
f
ln
2
2
V
a
b V
RT
p
RT ) b V (
V
a
p
,
_
+
dV
V
a 2
) b V (
RT
dp
2 2
,
_
p
p 2
2
Vdp
RT
2
f
f
ln
dV
V
a 2
) b V (
RT
V
RT
2
f
f
ln
2 2
V
V 2
2
,
_
V
V
2
V
V
2
2 2
RTV
aVdV 2
) b V (
VdV
V
V
2
V
V 2
2 2
) b V (
VdV
RTV
a 2
f
f
ln
+
V
V
2
2 2
2
) b V (
VdV
RTV
a 2
RTV
a 2
f
f
ln
V
V
2
2
2
) b V (
VdV
RTV
a 2
f
f
ln
2
) b V (
VdV
du dV
u b V
Since V
0
is at a very low pressure, it is very large. As an approximation which is valid,
0 0
V b V
This equation gives the expression for fugacity of a gas that follows Van der Waals
equation.
83
,
_
+ du
u
b
u
2
2
2
u
du ) b u (
u
b
u ln
b V
b
) b V ln(
b V
b
b V
b
b V
b V
ln
) b V (
VdV
2 2
V
V
2
2
,
_
b V
b
b V
b V
ln
2
,
_
2
) b V (
VdV
V
V
2
2
2
) b V (
VdV
RTV
a 2
f
f
ln
b V
b
b V
b V
ln
) b V (
VdV
2
V
V
2
2
,
_
b V
b
b V
b V
ln
RTV
a 2
f
f
ln
2 2
+
,
_
b V
b
V
b V
ln
RTV
a 2
p
f
ln
2 2
+
,
_
b V
b
V ln ) b V ln(
RTV
a 2
p ln f ln
2 2
+ +
b V
b
p
RT
ln ) b V ln(
RTV
a 2
2
+
,
_
+
b V
b
p ln ) RT ln( ) b V ln(
RTV
a 2
p ln f ln
2 2
+ +
RTV
a 2
b V
b
b V
RT
ln f ln
+
,
_
Approximate value of fugacity (Quick estimation):
Based on residual volume,
For low to moderate pressures,
And we know that
Assuming as an approximation, the residual volume may be assumed to be independent
of temperature, the above integral may be written as,
The above equation may be used for quick estimation of fugacity.
84
p d
RT p
f
ln
p
o
,
_
2
p
f
( ) 2 x x ln Lim
2 x
RT
p
2
p
f
RT
p
2
p
f
+
,
_
+
p
RT
V
RT
p
2
p
f
,
_
+
p
RT
V
RT
p
p f
2
,
_
+
p
RT
V
RT
p
p f
2
p
RT
V p
p f
2
+
RT
V p
f
2
Você também pode gostar
- Thermo NotesDocumento129 páginasThermo NotesManoj MallickAinda não há avaliações
- Thermodynamics: Basic ConceptsDocumento5 páginasThermodynamics: Basic ConceptsBijayaThaniAinda não há avaliações
- Thermo PDFDocumento129 páginasThermo PDFbansallove2008Ainda não há avaliações
- Thermodynamics Thermodynamics Is The Science That Deals With Heat and Work and Those Properties ofDocumento16 páginasThermodynamics Thermodynamics Is The Science That Deals With Heat and Work and Those Properties oftagoreboopathyAinda não há avaliações
- Eng Komolafe Thermodynamics Lecture Note. (Module 1-4) DocxDocumento35 páginasEng Komolafe Thermodynamics Lecture Note. (Module 1-4) DocxOyedotun Tunde100% (1)
- B T D NotesDocumento38 páginasB T D NotesvikramvivAinda não há avaliações
- Unit 1Documento31 páginasUnit 1araz_1985Ainda não há avaliações
- PIKEMDocumento18 páginasPIKEMFlorenceAinda não há avaliações
- 470 - Mce 204 Lecture Note 2Documento61 páginas470 - Mce 204 Lecture Note 2Wahyu WijanarkoAinda não há avaliações
- Introduction To ThermodynamicDocumento7 páginasIntroduction To Thermodynamicrskr_tAinda não há avaliações
- 1 BmeDocumento44 páginas1 BmepmagrawalAinda não há avaliações
- Me6301 Engineering Thermodynamics - Lecture NotesDocumento139 páginasMe6301 Engineering Thermodynamics - Lecture NotesBIBIN CHIDAMBARANATHAN100% (5)
- Metallurgical Thermodynamics Notes 1Documento16 páginasMetallurgical Thermodynamics Notes 1Nigel FaranandoAinda não há avaliações
- Cet Question BankDocumento42 páginasCet Question BankSruthi ChallapalliAinda não há avaliações
- CH I Concepts in ThermoDocumento14 páginasCH I Concepts in ThermoIsaac S Whuling IIIAinda não há avaliações
- Thermodynamics: Equilibrium StateDocumento7 páginasThermodynamics: Equilibrium Statemukesh3021Ainda não há avaliações
- TD NotesDocumento69 páginasTD NotesAnil ThotaAinda não há avaliações
- Chapter 1thermodynamicsDocumento10 páginasChapter 1thermodynamicsMatthew SmithAinda não há avaliações
- Me8391 Etd Lecture NotesDocumento137 páginasMe8391 Etd Lecture NotesSurya SAinda não há avaliações
- TD Lecture Notes PDFDocumento93 páginasTD Lecture Notes PDFMeenakshi SinghAinda não há avaliações
- PHẦN BÀI GHI CHÉPDocumento7 páginasPHẦN BÀI GHI CHÉPẨn DanhAinda não há avaliações
- Thermodynamics and ThermochemistryDocumento34 páginasThermodynamics and ThermochemistryBIJAY GAUTAMAinda não há avaliações
- Chemical Engineering Thermodynamics - Unit 1: EnergyDocumento10 páginasChemical Engineering Thermodynamics - Unit 1: EnergyaargovindAinda não há avaliações
- Thermodynamics 2 MarksDocumento23 páginasThermodynamics 2 MarksSanthana BharathiAinda não há avaliações
- BasicsDocumento65 páginasBasicsBas RamuAinda não há avaliações
- Me 291 Introduction To Mechechanical EngineeringDocumento11 páginasMe 291 Introduction To Mechechanical EngineeringDaniel Deng KuolAinda não há avaliações
- Thermodynamics Theory EDocumento45 páginasThermodynamics Theory Ethinkiit100% (1)
- Thermal EngineeringDocumento10 páginasThermal EngineeringGanesh Datt SharmaAinda não há avaliações
- ThermodynamicsDocumento192 páginasThermodynamicsDeepam SharmaAinda não há avaliações
- Unit-1 - Review of ThermodynamicsDocumento9 páginasUnit-1 - Review of ThermodynamicsiswaryaAinda não há avaliações
- Lecture 2 - Heat and WorkDocumento5 páginasLecture 2 - Heat and WorkMuhammadHamzaAinda não há avaliações
- ThermodynamicsDocumento60 páginasThermodynamicsMahender ThotakuriAinda não há avaliações
- 2 & 16 MarksDocumento23 páginas2 & 16 Markstamilselvan nAinda não há avaliações
- QuestionsDocumento8 páginasQuestionsAntonioAinda não há avaliações
- SCHX1014 - Chemical Engineering Thermodynamics - Unit 1: EnergyDocumento18 páginasSCHX1014 - Chemical Engineering Thermodynamics - Unit 1: EnergyShanmuga PriyaAinda não há avaliações
- Summary of Second Book About Law of Thermodynamics 1Documento12 páginasSummary of Second Book About Law of Thermodynamics 1Batak CyberTeamAinda não há avaliações
- Bme NotesDocumento44 páginasBme Notestempoterrace2306Ainda não há avaliações
- TDDocumento23 páginasTDB. RanjitAinda não há avaliações
- Chapter 1thermodynamicsDocumento9 páginasChapter 1thermodynamicsStanly ThomasAinda não há avaliações
- TD Basic ConceptsDocumento60 páginasTD Basic ConceptsSK.FARAZ HUSSAINAinda não há avaliações
- ATD Unit 1Documento39 páginasATD Unit 1Mr. P. Ramkumar MECHAinda não há avaliações
- Page 1 of 20 Prepared by G.RadhaboyDocumento20 páginasPage 1 of 20 Prepared by G.RadhaboyMani KandanAinda não há avaliações
- Unit 1 Lecture 1.0 Thermodynamic EquilibriumDocumento11 páginasUnit 1 Lecture 1.0 Thermodynamic Equilibriumsrijal kunwarAinda não há avaliações
- Module 1 NotesDocumento33 páginasModule 1 NoteskrbautoAinda não há avaliações
- Engineering ThermodynamicsDocumento30 páginasEngineering ThermodynamicsAddisu DagneAinda não há avaliações
- Asic Mechanical Engineering: Unit-1 Part-1 ThermodynamicsDocumento99 páginasAsic Mechanical Engineering: Unit-1 Part-1 ThermodynamicsSanjiv ParabAinda não há avaliações
- ME - 2307 - 1 - Thermodynamics BasicsDocumento31 páginasME - 2307 - 1 - Thermodynamics Basicsআজিজুর রহমান চৌধুরীAinda não há avaliações
- Thermodynamics: Basic DefinitionsDocumento8 páginasThermodynamics: Basic DefinitionsAnu RadhaAinda não há avaliações
- Thermodynamics Lecture 1Documento38 páginasThermodynamics Lecture 1MarkJude MorlaAinda não há avaliações
- 6 Thermodynamics - TextbooksDocumento86 páginas6 Thermodynamics - Textbooksmansoorshaik1991Ainda não há avaliações
- Bme Module Total SyllabusDocumento120 páginasBme Module Total Syllabussibaprasadpanda123456Ainda não há avaliações
- Thermodynamics Unit 1 NotesDocumento49 páginasThermodynamics Unit 1 Noteskapilraj_mech100% (1)
- Chapter 2, First Law of ThermodynamicsDocumento30 páginasChapter 2, First Law of ThermodynamicsMohamed AbdelaalAinda não há avaliações
- Physics 110 Lecture 3 A Glimpse of Entropy: 1 Reversible and Irreversible ProcessesDocumento11 páginasPhysics 110 Lecture 3 A Glimpse of Entropy: 1 Reversible and Irreversible ProcessesRahul BhattAinda não há avaliações
- Thermodynamics II - LectureDocumento82 páginasThermodynamics II - LectureJohn Panopio100% (1)
- System, Law of ThermodynamicDocumento31 páginasSystem, Law of ThermodynamicsamAinda não há avaliações
- “Foundations to Flight: Mastering Physics from Curiosity to Confidence: Cipher 4”: “Foundations to Flight: Mastering Physics from Curiosity to Confidence, #4No Everand“Foundations to Flight: Mastering Physics from Curiosity to Confidence: Cipher 4”: “Foundations to Flight: Mastering Physics from Curiosity to Confidence, #4Ainda não há avaliações
- Composite Materials and StructuresDocumento319 páginasComposite Materials and Structuresravindrababug100% (1)
- Chapter 2Documento28 páginasChapter 2ravindrababugAinda não há avaliações
- Yeild CriterionDocumento16 páginasYeild CriterionravindrababugAinda não há avaliações
- Lab Manual AnsysDocumento232 páginasLab Manual AnsyssharanmechAinda não há avaliações
- Static Failure Theories: Uniaxial TestDocumento11 páginasStatic Failure Theories: Uniaxial TestsantoshAinda não há avaliações
- Non TradDocumento70 páginasNon TradHelliel OliveiraAinda não há avaliações
- Bauschinger EffectDocumento206 páginasBauschinger EffectNiculae BulibasaAinda não há avaliações
- Handbook of Casting DefectsDocumento90 páginasHandbook of Casting DefectsAnshuman Roy90% (10)
- Tut Failure TheoriesDocumento39 páginasTut Failure TheoriesKamil Hakan TuranAinda não há avaliações
- Unit 11Documento20 páginasUnit 11Venkatesh Gangadhar100% (1)
- 6589789IC EngineDocumento21 páginas6589789IC EngineravindrababugAinda não há avaliações
- Section-A: Q. 1.1. (A) Explain Machine With Suitable ExamplesDocumento59 páginasSection-A: Q. 1.1. (A) Explain Machine With Suitable ExamplesravindrababugAinda não há avaliações
- Yield CriterionDocumento36 páginasYield CriterionravindrababugAinda não há avaliações
- Strain Gauges AnalysisDocumento1 páginaStrain Gauges AnalysisravindrababugAinda não há avaliações
- Structural MechanicsDocumento111 páginasStructural MechanicsDirkPons100% (5)
- Dynamics of MachinesDocumento176 páginasDynamics of MachinesAndré Da Luz Moreira100% (1)
- 1127 Sharygin, A. V., J. P. O'Connell, and R. H. Wood Ind. Eng. Chem. Res., 35 2808 (1996) .Documento5 páginas1127 Sharygin, A. V., J. P. O'Connell, and R. H. Wood Ind. Eng. Chem. Res., 35 2808 (1996) .CHIRE SARAYASI MANUELAinda não há avaliações
- General Chemistry Grade 12 ModuleDocumento90 páginasGeneral Chemistry Grade 12 ModuleJELANY AQUINOAinda não há avaliações
- T-4 Handbook of Material Properties Data Bases PDFDocumento382 páginasT-4 Handbook of Material Properties Data Bases PDFhamsterAinda não há avaliações
- Formation Evaluation by Paul GloverDocumento143 páginasFormation Evaluation by Paul GloverPraise Koobee100% (2)
- Gpa Research BrochureDocumento28 páginasGpa Research Brochuresyukur10% (1)
- Gen Chem Ii ReviewerDocumento10 páginasGen Chem Ii ReviewerKristine VenusAinda não há avaliações
- Supercritical CO2: Properties and Technological Applications - A ReviewDocumento38 páginasSupercritical CO2: Properties and Technological Applications - A ReviewXuân ĐứcAinda não há avaliações
- Liquid Liquid EquilibriumDocumento9 páginasLiquid Liquid EquilibriumLucas_ABAinda não há avaliações
- Taller Aspen TermodinámicaDocumento3 páginasTaller Aspen TermodinámicaJuanda BarbosaAinda não há avaliações
- تقرير عن التجربة الاولى في الثرموداينمك 1Documento7 páginasتقرير عن التجربة الاولى في الثرموداينمك 1أحمد ال عيسىAinda não há avaliações
- Department of ChemistryDocumento15 páginasDepartment of ChemistryWorcPrimerAinda não há avaliações
- Volumetric Properties of Pure FluidsDocumento19 páginasVolumetric Properties of Pure FluidsgAinda não há avaliações
- PVTsim Tutorial CalsepDocumento140 páginasPVTsim Tutorial CalsepEngineer theos100% (3)
- Brochures Phywe Tess Che 2010Documento108 páginasBrochures Phywe Tess Che 2010AtomuusAinda não há avaliações
- Phase BehaviorDocumento44 páginasPhase Behaviorforeruner343Ainda não há avaliações
- Virial Equation of State 2Documento7 páginasVirial Equation of State 2dnanaAinda não há avaliações
- Formation Evaluation MSC Course Notes Paul GloverDocumento148 páginasFormation Evaluation MSC Course Notes Paul GloverwamilovkerimAinda não há avaliações
- NH3&H2O Props EnglishDocumento53 páginasNH3&H2O Props EnglishPRASANNAAinda não há avaliações
- Chapter 6-Single Phase Systems 1Documento16 páginasChapter 6-Single Phase Systems 1Abdussalam Al-hakimi Mohd TahirAinda não há avaliações
- Supercritical Fluid Extraction: A New Technology To Herbals: Vaibhav Shinde and Kakasaheb MahadikDocumento8 páginasSupercritical Fluid Extraction: A New Technology To Herbals: Vaibhav Shinde and Kakasaheb Mahadikanwar hasanAinda não há avaliações
- ENG101 Acidizing L N2 - #11 - Nitrogen Physical Properties Rev2Documento80 páginasENG101 Acidizing L N2 - #11 - Nitrogen Physical Properties Rev2danielmcaeAinda não há avaliações
- Los Diagramas de Pourbaix para El Sistema Níquel-Agua Se Extienden A Condiciones Subcríticas y Bajo-SupercríticasDocumento7 páginasLos Diagramas de Pourbaix para El Sistema Níquel-Agua Se Extienden A Condiciones Subcríticas y Bajo-SupercríticasJoseBautistaAinda não há avaliações
- Designing For Pressure Safety Valves in Supercritical ServiceDocumento4 páginasDesigning For Pressure Safety Valves in Supercritical ServicelaquetengoAinda não há avaliações
- CH 222 Exam 2 Practice CombinedDocumento23 páginasCH 222 Exam 2 Practice CombinedSick JaysAinda não há avaliações
- Section VII, Nature of Pure Matter and Various Steam Tables: Refrigeration and Air Conditioning Principle LectureDocumento169 páginasSection VII, Nature of Pure Matter and Various Steam Tables: Refrigeration and Air Conditioning Principle LectureMuhammad RaflyAinda não há avaliações
- SFC PPT 2Documento30 páginasSFC PPT 2govind ashokraoAinda não há avaliações
- PET 521 A Natural Gas by Engr DR AnyadiegwuDocumento60 páginasPET 521 A Natural Gas by Engr DR Anyadiegwudavidchinedu008Ainda não há avaliações
- ME 231 Montazami Whharris 9-10-18 SOLUTIONDocumento4 páginasME 231 Montazami Whharris 9-10-18 SOLUTIONEduardo Perez UriegasAinda não há avaliações
- Critical Properties of Crude OilDocumento11 páginasCritical Properties of Crude Oilmuhammad usman aslamAinda não há avaliações
- Retrograde PhenomenonDocumento1 páginaRetrograde PhenomenonsamarAinda não há avaliações