Chapter Three

Describing Data: Numerical Measures

GOALS
When you have completed this chapter, you will be able to:
ONE
Calculate the arithmetic mean, median, mode, weighted
mean, and the geometric mean.
TWO
Explain the characteristics, uses, advantages, and
disadvantages of each measure of location.
THREE
Identify the position of the arithmetic mean, median,
and mode for both a symmetrical and a skewed
distribution.
Goals
3- 1
FOUR
Compute and interpret the range, the mean deviation, the
variance, and the standard deviation of ungrouped data.

Describing Data: Numerical Measures
FIVE
Explain the characteristics, uses, advantages, and
disadvantages of each measure of dispersion.
SIX
Understand Chebyshevs theorem and the Empirical Rule as
they relate to a set of observations.
Goals
Chapter Three
3- 2
Characteristics of the Mean
It is calculated by
summing the values
and dividing by the
number of values.
It requires the interval scale.
All values are used.
It is unique.
The sum of the deviations from the mean is 0.
The Arithmetic Mean
is the most widely used
measure of location and
shows the central value of the
data.
The major characteristics of the mean are:
Average
Joe
3- 3
Population Mean
N
X

=
where
is the population mean
N is the total number of observations.
X is a particular value.
E indicates the operation of adding.
For ungrouped data, the
Population Mean is the
sum of all the population
values divided by the total
number of population
values:
3- 4
Example 1
500 , 48
4
000 , 73 ... 000 , 56
=
+ +
= =

N
X

Find the mean mileage for the cars.

A Parameter is a measurable characteristic of a
population.
The Kiers
family owns
four cars. The
following is the
current mileage
on each of the
four cars.
56,000
23,000
42,000
73,000
3- 5
Sample Mean
n
X
X
E
=
where n is the total number of
values in the sample.
For ungrouped data, the sample mean is
the sum of all the sample values divided
by the number of sample values:
3- 6
Example 2
4 . 15
5
77
5
0 . 15 ... 0 . 14
= =
+ +
=
E
=
n
X
X
A statistic is a measurable characteristic of a sample.
A sample of
five
executives
received the
following
bonus last
year ($000):
14.0,
15.0,
17.0,
16.0,
15.0
3- 7
Properties of the Arithmetic Mean
Every set of interval-level and ratio-level data has a
mean.
All the values are included in computing the mean.
A set of data has a unique mean.
The mean is affected by unusually large or small
data values.
The arithmetic mean is the only measure of location
where the sum of the deviations of each value from
the mean is zero.
Properties of the Arithmetic Mean
3- 8
Example 3
| | 0 ) 5 4 ( ) 5 8 ( ) 5 3 ( ) ( = + + = E X X
Consider the set of values: 3, 8, and 4.
The mean is 5. Illustrating the fifth
property
3- 9
Weighted Mean
)
2 1
)
2 2 1 1
... (
... (
n
n n
w
w w w
X w X w X w
X
+ +
+ + +
=
The Weighted Mean of a set of
numbers X
1
, X
2
, ..., X
n
, with
corresponding weights w
1
, w
2
,
...,w
n
, is computed from the
following formula:
3- 10
Example 4
89 . 0 $
50
50 . 44 $
15 15 15 5
) 15 . 1 ($ 15 ) 90 . 0 ($ 15 ) 75 . 0 ($ 15 ) 50 . 0 ($ 5
= =
+ + +
+ + +
=
w
X
During a one hour period on a
hot Saturday afternoon cabana
boy Chris served fifty drinks.
He sold five drinks for $0.50,
fifteen for $0.75, fifteen for
$0.90, and fifteen for $1.10.
Compute the weighted mean of
the price of the drinks.
3- 11
The Median
There are as many
values above the
median as below it in
the data array.
For an even set of values, the median will be the
arithmetic average of the two middle numbers and is
found at the (n+1)/2 ranked observation.
The Median is the
midpoint of the values after
they have been ordered from
the smallest to the largest.
3- 12
The ages for a sample of five college students are:
21, 25, 19, 20, 22.
Arranging the data
in ascending order
gives:

19, 20, 21, 22, 25.

Thus the median is
21.
The median (continued)
3- 13
Example 5
Arranging the data in
ascending order gives:

73, 75, 76, 80

Thus the median is 75.5.
The heights of four basketball players, in inches,
are: 76, 73, 80, 75.
The median is found
at the (n+1)/2 =
(4+1)/2 =2.5
th
data
point.
3- 14
Properties of the Median
There is a unique median for each data set.
It is not affected by extremely large or small
values and is therefore a valuable measure of
location when such values occur.
It can be computed for ratio-level, interval-
level, and ordinal-level data.
It can be computed for an open-ended
frequency distribution if the median does not
lie in an open-ended class.
Properties of the Median
3- 15
The Mode: Example 6
Example 6: The exam scores for ten nursing
students are: 81, 93, 84, 75, 68, 87, 81, 75, 81, 87.
Because the score of 81 occurs the most often, it is the
mode.
Data can have more than one mode. If it has two
modes, it is referred to as bimodal, three modes,
trimodal, and the like.
The Mode is another measure of location and
represents the value of the observation that appears
most frequently.
3- 16
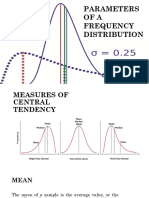
Symmetric distribution: A distribution having the
same shape on either side of the center
Skewed distribution: One whose shapes on either
side of the center differ; a nonsymmetrical distribution.
Can be negatively skewed, or positively skewed
The Relative Positions of the Mean, Median, and Mode
3- 17
The Relative Positions of the Mean, Median, and Mode:
Symmetric Distribution
Zero skewness Mean
=Median
=Mode
Mode
Median
Mean
3- 18
The Relative Positions of the Mean, Median, and Mode:
Right Skewed Distribution
Positively skewed: Mean and median are to the right of the
mode.
Mean>Median>Mode
Mode
Median
Mean
3- 19
Negatively Skewed: Mean and Median are to the left of the Mode.





Mean<Median<Mode
The Relative Positions of the Mean, Median, and
Mode: Left Skewed Distribution
Mode
Mean
Median
3- 20
Dispersion
refers to the
spread or
variability in
the data.
Measures of dispersion include the following: range,
mean deviation, variance, and standard
deviation.
Range = Largest value Smallest value
Measures of Dispersion
0
5
10
15
20
25
30
0 2 4 6 8 10 12
3- 21
The following represents the scores of the 25 master of
Nursing students during the first long examination.
65.0 60.0 59.0 81.0 73.0
48.0 95.0 63.0 92.0 53.0
78.0 56.0 79.0 95.0 78.0
80.0 89.0 79.0 97.0 69.0
65.0 77.0 80.0 83.0 75.0
Example 9
Highest score:97
Lowest score:48
Range = Highest value lowest value
= 97 - 48
= 49
3- 22
Mean
Deviation
The arithmetic
mean of the
absolute values
of the
deviations from
the arithmetic
mean.
The main features of the
mean deviation are:
All values are used in the
calculation.
It is not unduly influenced by
large or small values.
Mean Deviation
MD =
X - X
n
3- 23
The weights of a sample of crates containing books
for the bookstore (in pounds ) are:
103, 97, 101, 106, 103
Find the mean deviation.
X = 102
The mean deviation is:
4 . 2
5
5 4 1 5 1
5
102 103 ... 102 103
=
+ + + +
=
+ +
=
E
=
n
X X
MD
Example 10
3- 24
Variance: the
arithmetic mean
of the squared
deviations from
the mean.
Standard deviation: The square
root of the variance.
Variance and standard Deviation
3- 25
Not influenced by extreme values.
All values are used in the calculation.
The major characteristics of the
Population Variance are:
Population Variance
3- 26
Population Variance formula:
E (X - )
2
N
o
2
=
X is the value of an observation in the population
m is the arithmetic mean of the population
N is the number of observations in the population
o
=
Population Standard Deviation formula:
2
o
Variance and standard deviation
3- 27
Sample variance (s
2
)
s
2
=
E(X - X)
2
n-1
Sample standard deviation (s)
2
s s =
Sample variance and standard deviation
3- 28
40 . 7
5
37
= =
E
=
n
X
X
( ) ( ) ( )
30 . 5
1 5
2 . 21
1 5
4 . 7 6 ... 4 . 7 7
1
2 2
2
2
=

=

+ +
=

E
=
n
X X
s
Example 11
The hourly wages earned by a sample of five students are:
$7, $5, $11, $8, $6.
Find the sample variance and standard deviation.
30 . 2 30 . 5
2
= = = s s
3- 29
Chebyshevs theorem: For any set of
observations, the minimum proportion of the values
that lie within k standard deviations of the mean is at
least:






where k is any constant greater than 1.
2
1
1
k

Chebyshevs theorem
3- 30
Empirical Rule: For any symmetrical, bell-shaped
distribution:
About 68% of the observations will lie within 1s of
the mean
About 95% of the observations will lie within 2s of
the mean
Virtually all the observations will be within 3s of
the mean
Interpretation and Uses of the
Standard Deviation
3- 31
Bell -Shaped Curve showing the relationship between and . o
3o
2o 1o +1o +2o
+ 3o
68%
95%
99.7%
Interpretation and Uses of the Standard Deviation
3- 32
The Mean of Grouped Data
n
f X
X
E
=
The Mean of a sample of data
organized in a frequency
distribution is computed by the
following formula:
3- 33
From the example on hours spent in studying, we have
H o u r s s t u d y i n g C l a s s M i d p o i n t ( X ) F r e q u e n c y ( f ) f X
3 0 . 2 3 5 . 1 3 2 . 6 5 1 3 2 . 6 5
2 5 . 2 3 0 . 1 2 7 . 6 5 3 8 2 . 9 5
2 0 . 2 2 5 . 1 2 2 . 6 5 7 1 5 8 . 5 5
1 5 . 2 2 0 . 1 1 7 . 6 5 1 1 1 9 4 . 1 5
1 0 . 2 1 5 . 1 1 2 . 6 5 8 1 0 1 . 2
f X = 5 6 9 . 5

Therefore, the mean hours spent in studying is 569.5 /
30 = 18.98 hours
The Median of Grouped Data
) (
2
i
f
CF
n
L Median

+ =
where L is the lower limit of the median class, CF is the
cumulative frequency preceding the median class, f is
the frequency of the median class, and i is the class
width.
The Median of a sample of data organized in a
frequency distribution is computed by:
3- 35
Finding the Median Class
To determine the median class for grouped
data
Construct a cumulative frequency distribution.
Divide the total number of data values by 2.
Determine which class will contain this value. For
example, if n=30, 30/2 = 15, then determine which
class will contain the 15
th
value.
3- 36
From the example on hours spent in
studying
Hours
Studying
Lower
Limit

f Cumulative
Frequency

30.2 35.1 30.2 1 30
25.2 30.1 25.2 3 29
20.2 25.1 20.2 7 26
15.2 20.1 15.2 11 19
10.2 15.1 10.2 8 8

n/2 = 30/2 = 15. The second class (15.2 20.1)
having a cumulative frequency of 19 is the
median class. The lower limit is 15.2. The
cumulative frequency (CF) that precedes the
median class is 8. The frequency (f) of the
median class is 11.The class width, i = 5.
Therefore, the median is:
Median = 15.2 + (15-8)(5) = 18.4
11

The Mode of Grouped Data
The Mode for grouped data is
approximated by the formula


3- 39
|
|
.
|

\
|
+
+ =
2 1
1
d d
d
Lb Mo
(i)
where
L = lower limit of the modal class interval
d1 = diff. between the freq. of the modal CI
and the next class lower in value
d2 = diff. between the freq. of the modal CI
and the next class higher in value
i = class width
From the example on the hours spent in
studying, we have
the modal class is 15.2 20.1 with the highest
frequency of 11(L = 15.2)
d1 =11-8 = 3
d2 = 11-7 = 4
i = 5
Therefore, the mode is
Mode = 15.2 +[3/(3+4)](5) = 17.3
Since the Mean = 18.98 > median = 18.4> mode = 17.3,
therefore the distribution of the number of hours
spent in studying is positively skewed.
Variance for Grouped Data
( )
2
2
2
) 1 (

=

n n
fx fx n
s
where
n = sample size
f = frequency
x = class marks

From the example on hours spent in studying, we have
Hours studying X f fX fX
2

30.2 35.1 32.65 1 32.65 1066.02
25.2 30.1 27.65 3 82.95 2293.57
20.2 25.1 22.65 7 158.55 3591.16
15.2 20.1 17.65 11 194.15 3426.75
10.2 15.1 12.65 8 101.2 1280.18
fX=569.5 fX
2
=11657.68

19 . 29
870
25 . 25399
) 1 30 ( 30
) 5 . 569 ( ) 65 . 11657 ( 30
2
2
= =

= s
And the standard deviation is

S = (29.19)
1/2
= 5.4

Therefore, the variance is
Chapter Four
One-Sample Tests of Hypothesis
GOALS
When you have completed this chapter, you will be able to:
ONE
Define a hypothesis and hypothesis testing.
TWO
Describe the five step hypothesis testing procedure.
THREE
Distinguish between a one-tailed and a two-tailed test of
hypothesis.
FOUR
Conduct a test of hypothesis about a population mean.
Chapter Ten continued
GOALS
When you have completed this chapter, you will be able to:
FIVE
Conduct a test of hypothesis about a population proportion.
SIX
Define Type I and Type II errors.
One-Sample Tests of Hypothesis
What is a
Hypothesis?
What is a
Hypothesis?
A HYPOTHESIS is defined by Webster as
a tentative theory or supposition
provisionally adopted to explain certain
facts and to guide in the investigation of
others.

A statistical hypothesis is an
assertion or statement that may or may
not be true concerning one or more
population.
Example of Statistical
Hypotheses
A leading drug in the treatment of hypertension has
an advertised therapeutic success rate of 84%. A
medical researcher believes he has found a new
drug for treating hypertensive patients that has
higher therapeutic success rate than the leading
drug but with fewer side effects. He should assume
that it is no better than the leading drug and then
set out to reject this contention. The two
statements: the new drug is no better than the old
one (p = 0.84) and the new drug is better than the
old one (p > 0.84) are examples of statistical
hypothesis.
What is Hypothesis Testing?
Hypothesis testing
Based on sample
evidence and
probability theory
Used to determine whether the
hypothesis is a reasonable statement and
should not be rejected, or is unreasonable
and should be rejected
Types of Hypothesis



1. Null Hypothesis (Ho) - the hypothesis that two or more variables are not related or
that two or more statistics (e.g. means for two different groups) are not significantly
different. It is a negation of the theory that the researcher would like to derive. In the
above example, the statement the new drug is no better than the old one is an
example of a null hypothesis. It is usually constructed to enable the researcher to
evaluate his own theory or the research hypothesis. In other words, the null hypothesis
is stated with the sole purpose of rejecting it, thereby accepting the research
hypothesis. Equality symbol (=) is commonly used in stating the null hypothesis.

Types of Hypothesis


2. Alternative Hypothesis (H
1
) the hypothesis derived from the theory of the
investigator and generally state a specified relationship between two or more
variables or that two or more statistics significantly differ. In other words, it is the
operational statement of the investigators research hypothesis. The second
statement the new drug is better than the old one (above example) is an example
of alternative hypothesis. The symbols commonly used are >, < and =.
Two ways of stating the alternative hypothesis:

Predictive H
1
(One-tailed or directional) specifies the type of relationship existing
between two or more variables (e.g. direct or inverse relationship) or specifies the
direction of the difference between two or more statistics (e.g.
1
>
2
or
1
<
2
).
Non-predictive H
1
(Two-tailed or non-directional ) does not specify the type of
relationship or the direction of the difference ( e.g.
1
=
2
)


One-Tailed and Two-Tailed Tests
A test of any hypothesis where the alternative hypothesis is predictive such as
Ho:
1
=
2

H
1
:
1
>
2
or
1
<
2


is called a one-tailed test. The rejection region for the alternative hypothesis
1
>
2
lies
entirely in the right tail of the distribution, while the rejection region for the alternative
hypothesis
1
<
2
lies entirely in the left tail.

A test of any hypothesis where the alternative hypothesis is non-predictive such as
Ho:
1
=
2

H
1
:
1
=
2


is called a two-tailed test, since the rejection region is split into two equal parts
placed in each tail of the distribution.


More Examples of Stating Hypothesis


Example1. Suppose you want to study the association between job satisfaction of the
employees and the labor turnover in a certain private hospital.
Ho: There is no significant relationship between job satisfaction and the
labor turnover in a certain private school or stated differently, job satisfaction does
not significantly affect labor turnover
H
1
: There is an inverse relationship between job satisfaction and labor
turnover, more specifically, when job satisfaction decreases, labor turnover
increases.(predictive)


More Examples . . .

Example 2. A researcher is conducting a study to determine if suicide incidence among
teenagers can be attributed to drug use.
Ho: There is no significant difference between the suicide rates of teenagers
who use drugs and those who do not.
H
1
: Suicidal rates of teenagers who use drugs are significantly higher than the
suicidal rates of non-users.(predictive)
H
1
: There is a significant difference between the suicide rates of teenagers
who use drugs and those who do not.(non-predictive)

More Examples . . .



Example 3. A social researcher is conducting a study to determine if the level of womens
participation in community extension programs of the barangay can be affected by their
educational attainment, occupation, income, civil status, and age.
Ho : The level of womens participation in community extension programs is
not affected by their educational attainment, occupation, income, civil status and age.
H
1
: The level of womens participation in community extension programs is
affected by their educational attainment, occupation, income, civil status and age.

Hypothesis Testing
Do not reject null Reject null and accept alternate
Step 5: Take a sample, arrive at a decision
Step 4: Formulate a decision rule
Step 3: Identify the test statistic
Step 2: Select a level of significance
Step 1: State null and alternate hypotheses
Three
possibilities
regarding
means
H
0
:

= 0
H
1
:

= 0
H
0
:

= 0
H
1
:

> 0
H
0
:

= 0
H
1
:

< 0
Step One: State the null and alternate
hypotheses
The null
hypothesis
always contains
equality.
3 hypotheses
about means
Step Two: Select a Level of
Significance.
The probability of rejecting the null
hypothesis when it is actually true; the
level of risk in so doing.
Rejecting the null hypothesis
when it is actually true (o).
Accepting the null hypothesis
when it is actually false (|).
Level of Significance
Type I Error
Type II Error
Step Two: Select a Level of Significance.
Researcher
Null Accepts Rejects
Hypothesis H
o
H
o

H
o
is true


H
o
is false
Correct
decision
Type I
error
(o)
Type II
Error
(|)
Correct
decision
Risk table
Step Three: Select the
test statistic.
A value, determined from
sample information, used to
determine whether or not to
reject the null hypothesis.
Examples: z, t, F, _
2
Test statistic
z Distribution as a test statistic
n / o

=
X
z
The z value is based on the sampling
distribution of X, which is normally distributed
when the sample is reasonably large (recall
Central Limit Theorem).
Step Four: Formulate the decision rule.
Critical value: The dividing point between the region where the null hypothesis is
rejected and the region where it is not rejected.
0
1.65
Do not
reject
[Probability =.95]
Region of
rejection
[Probability=.05]
Critical value
Sampling Distribution
Of the Statistic z, a
Right-Tailed Test, .05
Level of Significance
Reject the null
hypothesis
and accept the
alternate
hypothesis if
Computed -z

< Critical -z

or
Computed z

> Critical z
Decision Rule
Decision Rule
Using the p-Value in
Hypothesis Testing
If the p-Value is larger than or equal
to the significance level, o, H
0
is not
rejected.
p-Value
The probability, assuming that the null hypothesis is true, of
finding a value of the test statistic at least as extreme as the
computed value for the test
Calculated from the probability
distribution function or by computer
Decision Rule
If the p-Value is smaller than the
significance level, o, H
0
is
rejected.
>.05
.10 p
>.01
.05 p
Interpreting p-values

SOME evidence H
o
is not true
>.001
.01 p
STRONG evidence H
o
is not true
VERY STRONG evidence H
o
is not
true
Step Five: Make a decision.
Movie
Test Concerning Means (o is known or n > 30) a sample mean is to be compared with
the population mean.
a.) Ho:

=
o
b.) Ho:

=
o
c.) Ho:

=
o

H
1
:

<
o
H
1
:

>
o
H
1
:

=
o


Test Statistic:

Rejection Region:
a.) Z < -Zo b.) Z > -Zo c.) Z < -Z

Z > Z
o/2


o
n x
z
o
) (
=
An Example
A private university hypothesized that the mean starting monthly salary of its
graduates is P8000 with a standard deviation of P1500. A sample of 25 employed
graduates showed an average starting salary of P7500. Test this hypothesis at 5% level of
significance.
Solution:
Ho:

= 8000
H1:

= 8000
Level of significance: o/2 = 0.05/2 = 0.025 (two-tailed)
Rejection Region: Z > 1.96 and Z s -1.96 (refer to Table A.1 Appendix)


Computation of the Test Statistic:
Given: = 7500, o = 900, n = 25







Decision: Since the value of the test statistic (z = -1.67) is greater than the tabular value
of 1.96, then do not reject Ho and conclude that the claim of the private university is
true.


67 . 1
1500
25 ) 8000 7500 ( ) (
=

=
o
n x
z
o
Test Concerning Means (o is unknown and n < 30)
a.) Ho:

=
o
b.) Ho:

=
o
c.) Ho:

=
o

H
1
:

<
o
H
1
:

>
o


H
1
:

=
o


Test Statistic:

Rejection Region:

a.) t < -t
o
b.) .) t > -t
o
c.) .) t < -t
o/2
and t > t
o/2



s
n x
t
o
) (
=
An Example
A perfume company claims that their best selling brand, Blue Ginger, has an average
purity of 87.9%. Twenty bottles were examined to have an average purity of 85.6% with a
standard deviation of 8.3%. Test at the 1% significance level whether the perfume
company is telling the truth.
Solution:
H
O
: The average purity of blue ginger is equal to 87.9% (

= 0.879).
H
1
: The average purity of blue ginger is less than 87.9%, or (

< 0.879).
Significance Level : 1%
Rejection Region: t s - 2.539 (with o = 0.01 and degrees of freedom of 19, i.e.20 1 = 19



Computation of the Test Statistic: t test









Decision: Since 1.24 is outside the rejection region, then we accept H
O
: at the 1%
significance level. Therefore, the average purity of blue ginger is equal or greater than
87.9%. Therefore, the perfume company is telling the truth.



856 . 0 = x
879 . 0 =
O

083 . 0 = s
20 = n
n
s
x
t
O

=
20
083 . 0
879 . 0 856 . 0
=
24 . 1 =
Test Concerning Proportion
Tests of hypotheses concerning proportions are required in many areas. A drug
manufacturer is certainly interested in knowing what fraction of the patients recover
after taking the medicine. In business, manufacturing firms are concerned about the
proportion of defective when shipment is made. A social researcher might be interested
in determining the proportion of people favoring the legalization of abortion in the
Philippines.

Steps in testing a proportion
1. Ho: p = p
o

2. H
1
: p < p
o
, p > p
o
or

p = p
o

Choose a level of significance of size o.
Establish the rejection region
Computation:

where p= sample proportion
p
0 =
population proportion
n = sample size
Make a decision that is, reject Ho if z falls in the rejection region, otherwise do not reject
Ho.


n
p p
p p
z
O O
O
) 1 (

=
An Example

A television station intends to stop airing a telenovela show, Maganda ang Buhay, if
less than 35% of its intended televiewers watch the said program. A random sample of
1500 households yields an average viewing percentage of 32.9%. Should the television
company pull out the airing of the show? Use the 5% significance level.

Solution:
H
O
: The average viewing percentage of the telenovela Maganda ang Buhay is equal
35% (p = .35).

H
1
: The average viewing percentage of the telenovela Maganda ang Buhay is less than
35% (p <.35)

Significance Level: 5%

Rejection Region:


o
z z < 65 . 1 < z
Computation of Test Statistics: z test











Decision: Since 1.71 is within the rejection region, then we reject H
O
at the 5%
significance level. Therefore, the average viewing percentage of the telenovela Maganda
ang Buhay is less than 35% and the television company should pull out the airing of the
show.


1500 = n 329 . 0 = p
35 . 0 =
O
p
n
p p
p p
z
O O
O
) 1 (

=
1500
) 35 . 0 1 ( 35 . 0
35 . 0 329 . 0

=
71 . 1 =
Exercises
1. A sample of size 60 has a mean of 12.8 and a standard deviation of 2.5. Test the
hypothesis that the population mean is 12 using a.) a one-tailed test at 0.01 level
and b.) a two-tailed test at 0.05 level.
2. Suppose it is known that the mean annual income of assembly line workers in a
certain plant is P100,000 with a standard deviation of P7000. You suspect that
workers with active union interests have higher than the average incomes and take
a random sample of 85 of these active members, obtaining a mean of P105,000.
Can you say that active union members have significantly higher incomes? Use 5%
level of significance.


3. Last year the employees of the city sanitation department donated an average of 250
pesos to the volunteer rescue squad. Test the hypothesis at 0.01 level that the average
contribution this year is still 250 if a random sample of 15 employees showed an average
of 265 pesos with a standard deviation of 15 pesos. Assume that the donations are
approximately normally distributed.
4. Suppose that in the past 40% of all adults favored capital punishment. Do we have
reason to believe that the proportion of adults favoring capital punishment today has
increased if, in a random sample of 200 adults 120 favor capital punishment? Use a 0.05
level of significance.

5. The average height of males in the freshmen class of a certain university has been
65.8 inches, with a standard deviation of 3.2 inches. Is there reason to believe that there
has been an increase in the average height if a random sample of 40 males in the
present freshmen class have an average height of 67.5 inches? Use a 1% level of
significance.
6.A researcher knows that the average height of Filipino women is 1.525 meters. A
random sample of 25 women was taken and was found to have a mean height of 1.572
meters, with a standard deviation of .12 meters. Is there reason to believe that the 25
women in the sample are significantly taller than the others at .05 level of significance?

7. A random sample of 100 recorded deaths in the Philippines during the past year showed an
average life span of 71.8 years with a standard deviation of 8.9 years. Does this seem to
indicate that the average life span today is greater than 70 years? Use a 0.05 level of
significance.
8. A mayoralty candidate in a certain city expects that approximately 60% of the voters will
favor him in the coming election. To support his claim, he let a social researcher conduct a
survey consisting of 100 randomly selected voters in the different barangays comprising the
city. Results showed that 70 interviewed voters favor this particular mayoralty candidate. Is
this sufficient evidence to conclude that the proportion of voters favoring this candidate in
the coming election is higher than what he expected. Use .01 level of significance.



Chapter Five
Two-Sample Tests of Hypothesis
GOALS
When you have completed this chapter, you will be able to:
TWO
Conduct a test of hypothesis regarding the difference in two
population proportions.
THREE
Conduct a test of hypothesis about the mean difference between
paired or dependent observations.
ONE
Conduct a test of hypothesis about the difference between two
independent population means.
Chapter Eleven continued
Two Sample Tests of Hypothesis
GOALS
When you have completed this chapter, you will be able to:

FOUR
Understand the difference between dependent and
independent samples.
Difference of Means Test ( o
1
and o
2
are
known) two sample means are being
compared.

a.) Ho:
1
=
2
b.) Ho:
1
=
2
c.) Ho:
1
=
2

H
1
:
1
<
2
H
1
:
1
>
2
H
1
:
1

=
2

Test Statistic:

2
2
2
1
2
1
0 2 1
) (
n n
d x x
z
o o
+

=
Rejection Region:
a.) Z < -Zo b.) Z > Zo c.) Z < -Z
o/2
or Z > Z
o/2

An Example
A university investigation team conducted a study to
determine whether car ownership of students affects
their academic performance. A random sample of 50
students who are non-car owners showed a grade
point average (GPA) of 85 with a standard deviation of
10.2 while a group of 60 car owners got an average
grade of 80 with a standard deviation of 8.9. Do the
data provide sufficient evidence to indicate that the
non-car owners are better than car owners in terms of
academic performance? Test using 5 % level of
significance.

Solution:
Let
1
= mean grade for non-car owners

2
= mean grade for car owners
Ho:
1
=
2


H
1
:
1
>
2
(one-tailed)
Level of significance: o= 0.05
Rejection Region: Z > 1.645 ( refer to Table A.1
Appendix)

Computation of the Test Statistic:
Given:
60 , 9 . 8 , 80
50 , 2 . 10 , 85
2 2 2 2
1 1 1
1
= = = =
= = = =
n s x
n s x
o
o
The value of the z statistic will be




Decision: Since the value of the test statistic (z=
2.71) is greater than the tabular value of
1.645, then reject Ho. The data provide
sufficient evidence to indicate non-car owners
have better academic performance than car
owners.

71 . 2
60
) 9 . 8 (
50
) 2 . 10 (
0 ) 80 85 ( ) (
2 2
2
2
2
1
2
1
0 2 1
=
+

=
+

=
n n
d x x
z
o o
Difference of Means Test ( o
1
= o
2
= o but unknown)
a.) Ho:
1
=
2
b.) Ho:
1
=
2
c.) Ho:
1
=
2

H
1
:
1
<
2
H
1
:
1
>
2
H
1
:
1
=
2

Test Statistic:



where

with degrees of freedom v = n
1
+ n
2
-2


2 1
0 2 1
1 1
) (
n n
Sp
d x x
t
+

=
2
) 1 ( ) 1 (
2 1
2
2 2
2
1 1
+
+
=
n n
s n s n
Sp
Rejection Region:
a.) t < -t
o
b.) t > t
o
c.) t < -t
o/2

t > t
o/2

An Example
A businessman is planning to put up either a computer
store or a video store. He randomly selected 10
computer stores and 10 video stores. The average weekly
incomes are P45,000 and P53,000 respectively with
corresponding standard deviations of P17,500 and
P15,000. At the 1% significance level, indicate whether
he should be convinced to put up a computer store or a
video store.

Solution:
Let
1
= mean weekly income of a computer stores

2
= mean weekly income of video stores
Ho:
1
=
2

H
1
:
1

2
(two-tailed)
Significance Level: 1%
Rejection Region: and

and t> 2.878


18 , 005 .
t t <
18 , 005 .
t t >
878 . 2 < t
Computation of Test Statistics: t test

(

+
+
+

=
2 1 2 1
2
2 2
2
1 1
2 1
1 1
2
) 1 ( ) 1 (
n n n n
s n s n
x x
t
10
2 1
= = n n
000 , 45
1
P x = 000 , 53
2
P x = 500 , 17
1
P = o 000 , 15
2
P = o
1 . 1
10
1
10
1
2 10 10
) 000 , 15 )( 1 10 ( ) 500 , 17 )( 1 10 (
000 , 53 000 , 45
2 2
=
(

+
+
+

= t
Decision: Since 1.1 is not within the
rejection region, then we accept H
O
: at the
1% significance level. Therefore, there is no
significant difference whether the
businessman puts up either a computer store
or video store. Therefore, opening a computer
store is as profitable as opening a video store.
Testing the Difference of Two Proportions

a) Ho: P
1
= P
2
b.) Ho: P
1
= P
2
c.) Ho: P
1
= P
2

H
1
: P
1
< P
2
H
1
: P
1
> P
2
H
1
: P
1
= P
2

Test Statistic:


where

Rejection Region:

a.) Z < -Zo b.) Z > Zo c.) Z < -Z
o/2
and Z > Z
o/2


(

=
2 1
2 1
1 1
) 1 (
n n
p p
p p
z
2
2
2
1
1
1
,
n
x
p
n
x
p = =
2 1
2 2 1 1
n n
p n p n
p
+

=
An Example

Consider random samples of 85 married couples last
year and another 100 couples this year. Data show
that 70 of last years married couples and 95 of this
years married couples are entrepreneurs. Using the
1% significance level, can it be stated that the
proportion of entrepreneurs has significantly
increased from last year to this year?
Solution: Let P
1
and P
2
be the true proportion of
married couples last year and this year who are
entrepreneurs, respectively.
H
O
: The proportion of entrepreneurs has not
significantly increased from last year to this
year, or (p
1
= p
2
).
H
1
: The proportion of entrepreneurs significantly
increased from last year to this year, or . (p
1
<
p
2
).
Significance Level : 1%
Rejection Region:

2 / o
z z <
005 .
z z <
33 . 2 < z
Computation of Test Statistics: z test

(

=
2 1
2 1
1 1
) 1 (
n n
p p
p p
z
85
1
= n 100
2
= n
823 . 0
85
70
1
= = p
95 . 0
100
95
2
= = p
89 . 0
100 85
) 95 . 0 ( 100 ) 823 . 0 ( 85
2 1
2 2 1 1
=
+

=
+

=
n n
p n p n
p
73 . 2
100
1
85
1
) 89 . 0 1 )( 89 . 0 (
95 . 0 823 . 0
=
(

= z
Decision: Since 2.73 is within the rejection
region, then reject H
O
: at the 1% significance
level. Therefore, the proportion of
entrepreneurs has significantly increased from
last year to this year.



Dependent Samples

Samples are called dependent if any one of the following
cases is true.
1. Before and after experiments - an experimental
variable is being measured in terms of its effectiveness.
This can be done by comparing the observations taken
from the same group before and after the introduction
of the experimental variable. If significant difference
exists, then the experimental variable is said to be
effective.
2.Two different groups matched pair by pair with respect
to some relevant characteristics. The primary purpose
of matching is to ensure that observations may differ
because of the experimental variable being tested.

A study is conducted to determine the effect of fraternity
membership to the performance of the students. One way
to measure the effect of fraternity membership
(experimental variable) is to consider say for instance 30
students and their performance (grades) before and after
membership to fraternity are being compared (case 1).
Another way is to compare the performance of two groups
of students, those who are fraternity members and those
who are non-fraternity members. The students in the first
group should be carefully matched with the students in the
second group with respect to some relevant characteristics
such as IQ level, study habits, gender, etc. This will ensure
that if a significant difference in the performance exists,
then this could solely be attributed to the fact that the first
group of students are fraternity members and the second
group are non-members.

a.) Ho:
1
=
2
b.) Ho:
1
=
2
c.) Ho:
1
=
2

H
1
:
1
<
2
H
1
:
1
>
2


H
1
:
1
=
2


Test Statistic:


where:
Sd
n d d
t
) (
0

=
) 1 (
) ( ) (
2

E E
=
n n
d d n
Sd
i
e
i
with v = n

1, n is the number of pairs

Rejection Region:
a.) t < -t
o
b.) t > t
o
c.) t < -t
o/2
and t > t
o/2

Example. If you wished to measure the
effectiveness of a new diet you would weigh
the dieters at the start and at the finish of the
program


Chapter Six
Analysis of Variance
GOALS
When you have completed this chapter, you will be able to:
ONE
Understand the purpose of Analysis of Variance.
TWO

Discuss the general idea of analysis of variance.
THREE
Organize data into a one-way

Chapter Twelve continued
Analysis of Variance
GOALS
When you have completed this chapter, you will be able to:
FOUR
Define and understand the terms treatments and blocks.
FIVE
Conduct a test of hypothesis among three or more treatment means.
Purpose of ANOVA

The Analysis of Variance (ANOVA for short) is a
technique designed to test whether or not more
than two sample means differ significantly from each
other.
In the preceding chapter, we learned that the t-test
or the z-test is used to test for the significance of
difference between two sample means. ANOVA,
therefore, which can be used to test for the equality
of several means simultaneously is an extension of
the t-test or the z-test which can handle only two
means at a time.

Illustration
Suppose for example, three methods of teaching (A,
B, C) are being compared in terms of effectiveness
and are being employed to three groups of students.
If the researcher uses the t-test, he will have to test
separately for the following pairs: A and B, A and C,
and B and C. In other words, the researcher would
be using the t-test formula three times which would
mean spending so much time and effort. Of course
there is a possibility that none of the pairs are
significantly different and so it is a waste of time and
effort on the part of the researcher.

Purpose of ANOVA
Now, if the researcher uses ANOVA, he could take all
the three sample means simultaneously and the test
stops if the conclusion arrived at is that of no
significant difference. However, if the conclusion
arrived at in using ANOVA shows significant
difference between the three sample means (A, B, C),
then the t-test must be used to find which pair of
means differ significantly. Another way is to use the
Duncans Multiple Range Test (DMRT) which is
beyond the scope of this manual.

Why the name analysis of variance?
The phrase analysis of variance means that we will
be analyzing the total variation in a set of
observations that can be attributed to specific
sources or causes of variation. With reference to the
above example, two such specific sources of
variations might be (1) actual differences in the three
methods that can be shown in the varying
performance of the three group of students
(treatment), and (2) chance, which in problems like
this is usually called experimental error.

The populations have equal standard
deviations.

ANOVA requires the following conditions

Underlying assumptions for ANOVA
The sampled populations follow the
normal distribution.
The samples are independent
Steps in ANOVA
The following are the steps and computations
involved in the Analysis of Variance technique.
Ho:
1
=
2
=
3
= . . . =
k
( for k sample
means)
H
1
: At least two means differ significantly
Test Statistic:
Rejection Region: F > F tabular (o, k-1, n-k)
where

MSE
MSTr
F =
1
) (

=
k
SSTr
Treatment MeanSquare MSTr
n
GrandTotal
n
ct
n
ct
n
ct
t esTreatmen SumofSquar SSTr
k
k
2
2
2
2
2
1
2
1
) (
...
) (

|
|
.
|

\
|
+ + + =
Computational Formulas
k n
SSE
Error MeanSquare MSE

= ) (
SSTr TSS esError SumofSquar SSE = ) (
n
GrandTotal
x Squares TotalSumof TSS
i
n
i
2
2
1
) (
) ( =
E
=
Source of Variation Degrees of
Freedom(df)
Sum of
Squares(SS)
Mean
Square(MS)
F
Value
Treatment k-1 SSTr MSTr F = MSTr/ MSE
Error n-k SSE MSE
Total n-1 TSS
Analysis of Variance (ANOVA) Table




ECP Restaurants specialize in meals for families. The owner recently
developed a new meat loaf dinner. Before making it a part of the regular
menu she decides to test it in several of her restaurants.
Example 1
She would like to know if there is a difference
in the mean number of dinners sold per day at
Restaurants A, B, and C. Use the .05
significance level.
Number of Dinners Sold by Restaurant
Restaurant
Day
A B C
Day 1
Day 2
Day 3
Day 4
Day 5
13
12
14
12
10
12
13
11
18
16
17
17
17
Example 1 continued
Solution:
H
o
:
A
=
B
=
C

H
1
: At least 2 means differ significantly
Level of significance is .05.
Example 2 continued
Rejection Region:
The numerator degrees of freedom, k-1, equal 3-1 or 2. The denominator degrees of
freedom, n-k, equal 13-3 or 10. The value of F at 2 and 10 degrees of freedom is 4.10.
Thus, H
0
is rejected if F>4.10
Example 2 continued
Using the data provided, the ANOVA
calculations follow.
Computations
= 13
2
+ 12
2
+ . . .+ 17
2
- (182)
2
/ 13

= 2634 2548 = 86

n
GrandTotal
x Squares TotalSumof TSS
i
n
i
2
2
1
) (
) ( =
E
=
25 . 76 2548 25 . 2624
13
) 182 (
)
5
85
4
46
4
51
(
) (
...
) (
2 2 2 2
2
2
2
2
2
1
2
1
= =
+ + =

|
|
.
|

\
|
+ + + =
n
GrandTotal
n
ct
n
ct
n
ct
t esTreatmen Sumof Squar SSTr
k
k
75 . 9 25 . 76 86 ) ( = = = SSTr TSS esError SumofSquar SSE
ANOVA Table
Source of
Variation
Sum of
Squares
Degrees
of
Freedom
Mean
Square
F
Treatments 76.25 3-1
=2
76.25/2
=38.125

38.125
.975
= 39.103
Error 9.75 13-3
=10
9.75/10
=.975
Total 86.00 13-1
=12
Example 1
continued
Example 1
continued
The ANOVA tables on the next two
slides are from the SPSS and EXCEL
systems
The mean number of meals
sold at the three locations is
not the same. Specifically, as
shown in the Duncans
Multiple Range Test, the meals
sold at Restaurant C is
significantly higher than A and
B, but A and B do not differ
significantly.
Since an F of 39.103 > the critical F of
4.10, the decision is to reject the null
hypothesis and conclude that
At least two of the treatment means are
not the same.
Example 1 continued
ANOVA
volsold
Sum of Squares df Mean Square F Sig.
Between Groups 76.250 2 38.125 39.103 .000
Within Groups 9.750 10 .975
Total 86.000 12



volsold
Duncan
Restaurant N Subset for alpha = 0.05
1 2
2 4 11.5000
1 4 12.7500
3 5 17.0000
Sig. .094 1.000
Means for groups in homogeneous subsets are displayed.

SUMMARY
Groups Count Sum Average Variance
Aynor 4 51 12.75 0.92
Loris 4 46 11.50 1.67
Lander 5 85 17.00 0.50
ANOVA
Source of Variation SS df MS F P-value F crit
Between Groups 76.25 2 38.13 39.10 2E-05 4.10
Within Groups 9.75 10 0.98
Total 86.00 12
Anova: Single Factor
Example 2
continued


Some common Post Hoc Tests are Duncans Multiple
Range Test of DMRT and Tukeys Test.
When I reject the null
hypothesis that the
means are equal, I want
to know which treatment
means differ.
Chapter Seven
Linear Regression and Correlation
GOALS
When you have completed this chapter, you will be able to:
ONE
Draw a scatter diagram.
TWO
Understand and interpret the terms dependent variable and independent variable.
THREE
Calculate and interpret the coefficient of correlation, the coefficient of determination,
and the standard error of estimate.
FOUR
Conduct a test of hypothesis to determine if the population coefficient of correlation is
different from zero.
Goals
Chapter Thirteen continued
Linear Regression and Correlation
GOALS
When you have completed this chapter, you will be able to:
FIVE
Calculate the least squares regression line and interpret the slope and intercept
values.
SIX
Construct and interpret a confidence interval and prediction interval for the
dependent variable.
SEVEN
Set up and interpret an ANOVA table.

Goals
Correlation Analysis
The Independent
Variable provides the
basis for estimation. It
is the predictor variable.
Correlation Analysis is a group of statistical techniques to
measure the association between two variables.
A Scatter Diagram is
a chart that portrays the
relationship between
two variables.
The Dependent
Variable is the variable
being predicted or
estimated.
Advertising Minutes and $ Sales
0
5
10
15
20
25
30
70 90 110 130 150 170 190
Advertising Minutes
S
a
l
e
s

(
$
t
h
o
u
s
a
n
d
s
)
The Coefficient of
Correlation, r
Negative values indicate an
inverse relationship and
positive values indicate a
direct relationship.
The Coefficient of Correlation (r) is a measure of the
strength of the relationship between two variables.
-1
1 0
Pearson's r
Also called Pearsons r and
Pearsons product moment
correlation coefficient.
It requires interval or ratio-
scaled data.
It can range from
-1.00 to 1.00.
Values of -1.00 or 1.00
indicate perfect and strong
correlation.
Values close to 0.0 indicate
weak correlation.
Perfect Negative
Correlation
0 1 2 3 4 5 6 7 8 9 10
10
9
8
7
6
5
4
3
2
1
0
X
Y
0 1 2 3 4 5 6 7 8 9 10
10
9
8
7
6
5
4
3
2
1
0
X
Y
Perfect Positive
Correlation
0 1 2 3 4 5 6 7 8 9 10
10
9
8
7
6
5
4
3
2
1
0
X
Y
Zero Correlation
0 1 2 3 4 5 6 7 8 9 10
10
9
8
7
6
5
4
3
2
1
0
X
Y
Strong Positive Correlation
Formula for r
We calculate the coefficient of correlation from the
following formula.
] ) ( ) ( ][ ) ( ) ( [
) )( (
2 2 2 2
y y n x x n
y x xy n
r
E E E E
E E E
=
Coefficient of Determination
It is the square of the coefficient of correlation.
It ranges from 0 to 1.
It does not give any information on the direction
of the relationship between the variables.
The coefficient of determination (r
2
) is the
proportion of the total variation in the dependent
variable (Y) that is explained or accounted for by the
variation in the independent variable (X).
Example

Suppose an investigator wants to determine
the extent to which a relationship exists
between size of income and the number of
years of education the individual has
completed. The following table shows the
data of ten individuals. Compute and
interpret r.


Individual # Y, Income (P,000) X, Education (years)
1 45 20
2 63 19
3 36 16
4 52 20
5 29 12
6 33 14
7 48 16
8 55 18
9 72 20
10 66 22

Solution
Preliminary computations of the above data:
n = 10 Ex = 177 Ey = 499 Exy= 9,173
Ex
2
= 3,221 Ey
2
= 26,793
Therefore,

] ) ( ) ( ][ ) ( ) ( [
) )( (
2 2 2 2
y y n x x n
y x xy n
r
E E E E
E E E
=
83 .
] ) 499 ( ) 26793 ( 10 ][ ) 177 ( ) 3221 ( 10 [
) 499 )( 177 ( ) 9173 ( 10
2 2
=


= r
The value of r
2
which is (.83)
2
= .6889 means that 68.89% of the total
variability in income is being explained by its linear relationship with
education.

Testing for the Significance of r
The sample correlation coefficient r is a value computed
from a random sample of n pairs of measurements.
Different random samples of size n from the same
population will generally produce different values of r.
Therefore, we need to test for the significance of the
computed r value. The null hypothesis will be = 0 against
the alternative that = 0. The rejection of Ho will lead to a
conclusion that the existing relationship is significant at
alpha level. However, failure to reject Ho would imply that
the relationship is not significant and thus it can be
attributed to chance.
From the above result, test the null hypothesis that there is
no linear relationship between income and education.. Use
a 0.05 level of significance.


Solution:
Ho: = 0
H
1
: = 0 (two-tailed)
Level of Significance: 0.05 / 2 = 0.025
Rejection Region: t > 2.306 and t < -2.306
Computation of the Test Statistic:



Decision: Since the value of the test statistic (t = 4.26) is
greater than the tabular value of 2.306, therefore
reject the null hypothesis of no linear relationship and
conclude that there is a significant relationship
between education and income. Specifically, the higher
the educational attainment, the higher the income
earned


26 . 4
) 83 (. 1
) 8 ( 83 .
1
) 2 (
2 2
=

=
r
n r
t
Regression
Analysis
The least squares criterion
is used to determine the
equation. That is the term
E(Y Y)
2
is minimized.
In Regression Analysis we use the independent
variable (X) to estimate the dependent variable (Y).
The relationship
between the
variables is linear.
Both variables
must be at least
interval scale.
The Y values are statistically independent. This means
that in the selection of a sample, the Y values chosen
for a particular X value do not depend on the Y values
for any other X values.
For each value of X, there is a group of Y values, and
these Y values are normally distributed.
Assumptions Underlying Linear Regression
The means of these normal
distributions of Y values all
lie on the straight line of
regression.
The standard deviations
of these normal
distributions are the
same.
Regression
Analysis
The regression equation is Y(hat)= a + bX (1)
where
Y(hat) is the predicted value of Y for any X.

a is the Y-intercept.
It is the estimated Y value when X=0

b is the slope of the line, or the average change
in Y for each change of one unit in X

The least squares principle is used to obtain a
and b.
Deterministic Model
Model (1) is called a deterministic model. It
gives an exact relationship between x and y.
This model expresses that y is determined
exactly by x and for a given value of x there is
one and only one value of y.
Probabilistic Model
However, in many cases the relationship between variables is
not exact. For instance, if y is food expenditure and x is
income, then model (1) would state that food expenditure
is determined by income only and that all households with
the same income will spend the same amount of food. But
food expenditure is determined by many other variables
such as household size, taste and preference which explains
why different households with the same income spend
different amounts of money for food. Hence, to take these
variables into considerations and to make our model
complete, we add another term to the right side of
model(1) called the random error term (c ).
The complete regression model is written as
y = A + Bx + c (2)


The regression model (2) is called a probabilistic model or
a statistical relationship.
The random error term (c) is included in the model to
represent the following two phenomena.
Missing or omitted variables. As mentioned earlier,
food expenditure is affected by many variables other
than income. The random error term is included to
capture the effect of all those missing variables that
have not been included in the model.
Random variation. Human behavior is unpredictable.
For example, a household may have many parties
during the month and may spend more than usual on
food during that month. This variation in food
expenditure may be called random variation.

Regression
Analysis
The least squares principle is used to obtain a and b.
The equations to determine a and b are:
2 2
) ( ) (
) )( (
x x n
y x xy n
b
E E
E E E
=
An Example
We have already established a significant linear relationship
between income and education (i.e. number of years in
education). We may now formulate an equation allowing us to
predict the income of a person given the number of years he
attended for his education. Referring to the above example,
we
find that
n = 10 EXi = 177 EYi = 499 EXi
2
= 3221 EYi
2
= 2679 EXiYi =
9173 Y(bar) = 49.9 X(bar) = 17.7

Therefore,



And


The model for prediction purposes is given by
.
87 . 3
) 177 ( ) 3221 ( 10
) 499 )( 177 ( ) 9173 ( 10
) ( ) (
) )( (
2 2 2
=

=
E E
E E E
=
x x n
y x xy n
b
59 . 18 ) 7 . 17 ( 87 . 3 9 . 49 = = = x b y a
x y 87 . 3 58 . 18 + =
The equation can be interpreted as per
additional year in
educational attainment, there corresponds 3.87
or 3,870 pesos
increase in the income of a person.


We can use the
regression equation
to estimate values
of Y.
The estimated income of a person
who have spent 16 years of
education will be:
34 . 43 ) 16 ( 87 . 3 58 . 18 = + = Income
Standard Error of Estimate (SEE)
a measure of the variability of the regression line, i.e. the
dispersion around the regression line
it tells how much variation there is in the dependent
variable between the raw value and the expected value in
the regression



this SEE allows us to generate the confidence interval on
the regression line as we did in the estimation of means


Exercise

It is generally known that the number of road accidents is
inversely proportional with road width. The following data
show the results of a study indicating the number of
accidents occurring annually at roads with different
widths:
Road width (in feet) (X)
75 52 60 33 22 40 70 35 55 80
Number of accidents (Y)
40 84 55 92 90 86 38 88 78 32
Draw the scatter diagram.
Find the correlation coefficient and test for its significance.
Establish a regression equation of the form Y = a + bX
Predict the number of accidents for a 50 ft road width.