1.

3 Parabolas 2
After this lesson, students should be able to:
Define a parabola
...
Find the equation of the
parabola with vertex (h, k)
and focus (h+p, k)
Find the equation of the
parabola with vertex (h, k)
and focus (h, k+p)
1.3 Parabolas 3
After this lesson, students should be able to:
Determine the vertex and
focus of a parabola by
completing the square
Introduce the applications
of parabola such as
suspension bridge, arch
and reflector
1.3 Parabolas 4

The parabola (from the Greek: ) is a conic
section generated by the intersection of a right
circular conical surface and a plane parallel to a
generating straight line of that surface.

A parabola can also defined as locus of points which
are equidistant from a given point (the focus) and a
given line (the directrix).

1.3 Parabolas 5
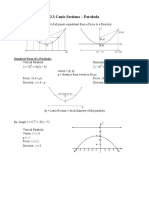
(y-k)
2
= 4p(x-h)
The equation of parabola with vertex V (h, k)
When p > 0
(Open Right)
When p < 0
(Open Left)
Vertex V(h,k)
Focus F(h+p, k)
Directrix x = h - p
Vertex V(h,k)
Focus F(h+p, k)
Directrix x = h - p
y
x
x = h - p
V(h,k)

F(h+p, k)
y
x
x = h - p
V(h,k)

F(h+p, k)
1.3 Parabolas 6
(x-h)
2
= 4p(y-k)
The equation of parabola with vertex V (h, k)
When p > 0
(Open Upwards)
When p < 0
(Open Downwards)
Vertex V(h,k)
Focus F(h, k+p)
Directrix y = k - p
Vertex V(h,k)
Focus F(h, k+p)
Directrix y = k - p
y
x
y = k - p
V(h,k)

F(h, k+p)
y
x
y = k - p
V(h,k)

F(h, k+p)
1.3 Parabolas 7

The equation

(y k)
2
= 4p(x h) or (x h)
2
= 4p (y k) {Standard Equation}

Ay
2
+ Dx + Ey + F = 0 or Ax
2
+ Dx + Ey + F = 0 {General Equation}

1.3 Parabolas 8
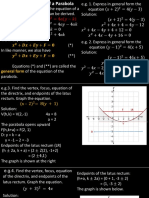
Example 1
Write the equation of the a parabola with
i) Vertex (0, 0) and focus, F (0, 5)
Sketch each graph.
Solution
** Equation of parabola is y
2
= 4px or x
2
= 4py

ii) When p = -5,
Equation of the Parabola
x
2
= 20y
Focus F ( 0, P)
F (0, -5)

Vertex, V (h, k)
V (0, 0)

Directrix, y= p
y = (-5) = 5
x
Y =5
y
F(0, -5)
V(0, 0)
.
.
1.3 Parabolas 9
Solution
** Equation of parabola is y
2
= 4px or x
2
= 4py

Example 2
Find the focus and directrix of the parabola
and sketch the graph
2
8
1
x y =
y = (1/8) x
2
X
2
= 8y
4p = 8
p = 2
Compare to
X
2
= 4py
Focus, F(0,2)
Directrix y = -2
Focus, F (0, p)
Directrix, y = -p
x
F (0,2)
V (0,0)
y
y = -2
1.3 Parabolas 10

Example 3
Find the equation of a parabola that has vertex at
origin, opens left, and passes through the point
P (-5,4).
Solution
** Equation of parabola is y
2
= 4px or x
2
= 4py
x
F (p, 0)
y

P(-5, 4)
V (0, 0)

y
2
= 4px
When P(-5,4)
y
2
= 4px
4
2
= 4p(-5)
P=-(4/5)


y
2
= 4px
y
2
= 4(-4/5)x
y
2
= (-16/5)x
1.3 Parabolas 11

Example 4
State the vertex, focus and directrix of
i) (y 2)
2
= 12 (x 3)
ii) (x - 1)
2
= 5 (y + 2)

Solution

i) (y 2)
2
= 12 (x 3)

Vertex, V(3, 2)

Focus, F(6,2)

Directrix, x =0

Compare with
(y-k)
2
= 4p(x h)
V(h, k)
Compare with
(y-k)
2
= 4p(x h)
4p = 12
P =3
F(h+p,k)
Compare with
(y-k)
2
= 4p(x h)
X=h-p

ii) (x 1)
2
= 5 (y + 2)

Vertex, V(1, -2)

Focus, F(1,-3/4)

Directrix, y =-13/4

Compare with
(x - h)2 = 4p(y - k)
V(h, k)
Compare with
(x - h)2 = 4p(y - k)
4p = 5
P = 5/4
F(h, k+p)
Compare with
(x - h)2 = 4p(y - k)
4p = 5
P = 5/4
y = k - p
1.3 Parabolas 12

Example 5
Sketch the graph of (y 2)
2
= 12 (x - 1).

Solution


(y 2)
2
= 12 (x - 1)

Vertex, V(h,k) V(1, 2)

Focus, F (h+p, k) F(4, 2)

Directrix, x = h p x = -2


x
y

X = -2
V(1 ,2) F(4, 2)
1.3 Parabolas 13

Example 6
Write down the equation of given parabola below in
standard form and state the coordinates of the vertex,
focus and the directrix. Sketch each graph.
i)x
2
+ 8x + 4y + 12 = 0

Solution
( )
( )
( ) ( )
( ) ( ) 1 y 4 4 x
0 1 y 4 4 x
0 4 4y 4 x
0 12 16 4y 4 x
0 12 4y
2
8
2
8
8x x
0 12 4y 8x x
2
2
2
2
2 2
2
2
=
= +
= +
= + +
= + +
|
.
|

\
|

|
.
|

\
|
+ +
= + + +
y
x

F(4,0)
V(4,1)
y = 2
1.3 Parabolas 14

Example 6
Write down the equation of given parabola below in
standard form and state the coordinates of the vertex,
focus and the directrix. Sketch each graph.
i)y
2
+ 8y -2x + 22 =0

Solution
( )
( )
( ) ( )
( ) ( ) 3
2
1
4 4
3 2 4
6 2 4
0 6 2 4
0 22 2 16 8
2
2
2
2
2

|
.
|

\
|
= +
=
=
= +
= + +
x y
x y
x y
x y
x y y
x
y

F(7/2, -4)
x = 5/2
V(3, -4)

1.3 Parabolas 15

Example 7
Find the equation of a parabola which satisfies the
following conditions, vertex (-1,-2) , its axis parallel to the
y-axis and the parabola passes through the point (3,6)

Solution
The parabola passes through (3, 6), then substitute

( ) ( )
( )
2
8 4 16
2 6 4 1 3
2
=
=
+ = +
p
p
p

(x+1)
2
=4p(y+2)
( ) ( )( )
( ) ( )
0 15 8 2
16 8 1 2
2 8 1
2 2 4 1
2
2
2
2
= +
+ = + +
+ = +
+ = +
y x x
y x x
y x
y x
The equation
of the
Parabola
1.3 Parabolas 16

Example 8
A necklace hanging between two fixed points A and B at
the same level. The length of the necklace between the two
point is 100 cm. The mid point of the necklace is 8 cm
below A and B. Assume that the necklace hangs in the form
of parabolic curve, find the equation of the curve

Solution

y
x
A
B
50 cm
50 cm
8 cm
General equation
( ) ( ) k y p h x = 4
2
Vertex V(0, -8)
A(-50,0), B(50,0)
( )
( ) 8
2
625

8
32
2500
4 thus
32
2500
8 0 4 50
0 and 50 substitute the 8 4
2
2
2
2
+ =
+ |
.
|

\
|
=
=
+ =
= = + =
y x
y x
p
p
y x y p x
) (
) ( ) (
1.3 Parabolas 17

Example 9
A gigantic gate to the entrance of a theme park in the shape of parabola is
constructed on a level ground. The horizontal distance between the end
points to the gigantic gate is 20m. The maximum height of the gigantic
gate from the ground is 5m. Calculate the height of the gigantic gate at a
horizontal distance of 4 meters from one of the end points.

Solution
y
x
4 cm
10 cm
5 cm
10 cm
General equation
( ) ( ) k y p h x = 4
2
Vertex V(0, 5)
A(-10,0), B(10,0)
( )( )
( ) 5 20
5 5 4 thus
5
20
100
5 0 4 10
0 and 10 substitute the 5 4
2
2
2
2
=
=
= =
=
= = =
y x
y x
p
p
y x y p x
) (
) ( ) (
( )
m y
y
y
y
x
2 . 3
64 20
100 20 36
5 20 6
6 when
2
=
=
+ =
=
=