1

1. Introduo.

O conceito de funo que hoje pode parecer simples o resultado de uma lenta e longa
evoluo histrica iniciada na Antiguidade quando, por exemplo, os matemticos Babilnicos
utilizaram tabelas de quadrado e de razes quadradas e cbicas ou quando os Pitagricos
tentaram relacionar a altura do som emitido por cordas submetidas mesma tenso com seu
comprimento. Nesta poca o conceito de funo no estava claramente definido.
S no sc. XVII, quando Descartes e Pierre Fermat introduziram as coordenadas
cartesianas, se tornou possvel transformar problemas geomtricos em problemas algbricos e
estudar analiticamente funes.
A Matemtica recebe assim um grande impulso a partir de observaes ou
experincias realizadas, a procurar e determinar a frmula ou funo que relaciona as
variveis em estudo. Por outro lado, a introduo de coordenadas, alm de facilitar o estudo
de curvas j conhecidas permitiu a criao de novas curvas, imagens geomtricas de
funes j definidas por relaes entre variveis.
Fermat deu conta das limitaes do conceito clssico de reta tangente a uma curva
como sendo aquela que encontrava a curva num nico ponto, para determinar uma tangente a
uma curva num ponto P considerou outro ponto Q sobre a curva; considerou a reta PQ secante
curva, obtendo deste modo retas PQ que se aproximavam duma reta t a que Fermat chamou
a reta tangente curva no ponto P.
Estas idias constituram o embrio do conceito de derivada e levou Laplace a
considerar Fermat o verdadeiro inventor do Clculo Diferencial. Contudo, Fermat no
dispunha de notao apropriada e o conceito de limite no estava ainda claramente definido.
S no sc. XIX Cauchy introduzia formalmente o conceito de limite e o conceito de derivada,
a partir do sc. XVII, com Leibniz e Newton, o Clculo Diferencial torna-se um instrumento
cada vez mais indispensvel pela sua aplicabilidade aos mais diversos campos da cincia.

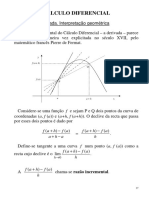
2. A Reta Tangente e a Derivada.

2.1 Reta Tangente.
Sejam f uma funo e p um ponto de seu domnio. Limites do tipo
( ) ( )

lim

ocorrem de modo natural tanto na geometria como na fsica.

Consideremos, por exemplo, o problema de definir a reta tangente ao grfico de f no
ponto (p, f(p)). Evidentemente, tal reta deve passar pelo ponto (p, f(p)); assim a reta tangente
fica determinada se dissermos qual deve ser seu coeficiente angular. Consideremos, ento, a
reta que passa pelos pontos (p, f(p)) e (x, f(x), conforme figura 2.1.

sx
f (x)
f(x) - f(p)

f(p)
x-p

x
Figura 2.1 Reta Secante ao grfico de .

Coeficiente angular de

( )

( )

Quando x tende a p, o coeficiente angular de

(

) = lim

tende a f(p), onde

( ) ( )

Observe que f(p) (leia: f linha de p) apenas uma notao para indicar o valor do
limite acima. Assim medida que x vai se aproximando de p, a reta
vai tendendo para a
posio da reta T da equao
( )=

)( ).

(1)

Figura 2.2 Reta Tangente ao grfico de .

natural, ento, definir a reta tangente em (p, f(p)) como sendo a reta de equao (1).
Suponhamos, agora, que s=f(t) seja a equao horria do movimento de uma partcula
vinculada a uma reta orientada na qual se escolheu uma origem. Isto significa dizer que a
funo f fornece a cada instante a abscissa ocupada pela partcula na reta. A velocidade mdia
( )
( )
da partcula entre os instantes e t definida pelo quociente

A velocidade (instantnea) da partcula no instante

v(t ) = lim

definida como sendo o limite

( ) ( )

Esses exemplos so suficientes para levar-nos a estudar de modo puramente abstrato

as propriedades do limite
lim

( ) ( )

2.2 - Derivada de uma Funo.

Sejam f uma funo e p um ponto de seu domnio. O limite
lim

( ) ( )

quando existe e finito, denomina-se derivada de f em p e indica-se por f (p) (leia: f linha de
p).

Assim,
( ) ( )

Se f admite derivada em p, ento diremos que f derivvel ou diferencivel em p.

Dizemos que f derivvel ou diferencivel em A
se f for derivvel em cada p A.
Diremos simplesmente, que f uma funo derivvel ou diferencivel se f for derivvel em
cada ponto de seu domnio.
(

) = lim

Observao: Segue das propriedades dos limites que

lim

( ) ( )
( + )
= lim

( )

Assim,
( ) = lim

( ) ( )

( ) = lim

( + )

( )

Conforme vimos na introduo a reta de equao ( ) = ( )( ), por

definio,a reta tangente ao grfico de f no ponto (p, f(p)). Assim, a derivada de f em p, o
coeficiente angular da reta tangente ao grfico de f no ponto de abscissa p.
Exemplos.
1 - Seja f(x) =

. Calcule:

a) f (1)
b) f (x)
c) f (-3)
Soluo:
) f (1) = lim

( ) (1)
= lim

Assim,
f(1) = 2.
(A derivada de f(x) =
) ( ) = lim

Como
( + )

1
= lim(

+ 1) = 2.

, em p=1, igual a 2.).

( + ) ( )
( + )
= lim

2 +
= 2 + , 0

Segue que
( )
= lim(2 + ) = 2 .

Portanto,
f(x) =
f(x)=2x.
Observe que f(x) = 2x uma frmula que nos fornece a derivada de f(x) =
x real.
)Segue de ( )que
f(-3) = 2 (-3) = -6.

, em todo

2 - Seja f(x) =

. Determine a equao da reta tangente ao grfico de f no ponto:

a) (1, f(1)).

b) (-1, f(-1)).

Soluo:
a) A equao da reta tangente em (1, f(1))
y f(1) = f (1) (x 1)

( 1) = 1 = 1
( ) = 2 (exemplo 1, item b)

(1) = 2

Substituindo em (1), vem

y 1 = 2(x 1) ou y = 2x 1.
Assim y = 2x 1 a equao da reta tangente ao grfico de f(x) =

, no ponto (1 ,

f(1)).
b) A equao da reta tangente em (1, f(1)) y f(1) = f(1) (x-(1)) ou
y f(1) = f(1) (x+ 1)
f(1) = (1) = 1
f(p) = 2p f (1)
1 = 2( + 1)

substituindo esses valores na equao vem

= 2 1 Que a equao da reta tangente pedida.
y

y = 2x - 1
(1, f(1))

-1

y = - 2x - 1
Figura 2.3 grfico das retas tangentes de nos pontos (1, (1)) e (1, ( (1)).

3 - Seja f(x) = k uma funo constante. Mostre que f(x) = 0 para todo o x. (A derivada de uma
constante zero).
Soluo:
(

) = lim

( + ) ( )
.

Como f(x) = k para todo x, resulta f (x + h) = k para todo x e todo h, assim

(

) = lim

= lim 0 = 0.

4 Calcule a derivada de f(x) =

e use-a para determinar a inclinao da reta tangente
curva y = no ponto x = -1. Qual a equao da reta tangente nesse ponto?
Soluo:
A inclinao da reta tangente curva y = f(x) no ponto (c, f(x)) dada por
acordo com a definio de derivada,
(

) = lim

( ) = lim

( )=3

= f(c). De

( + ) ( )
( + )
= lim

+3

+ 3 + )

= lim (3

+3 + )

Nesse caso, a inclinao da reta tangente curva y =

3(1) = 3.

no ponto x = -1 f (-1) =

Para determinar a equao da reta tangente, precisamos tambm da coordenada y do

ponto de tangencia, y=(1) = -1. Assim, a reta tangente passa pelo ponto (-1, -1) com
inclinao trs. Usando a forma ponto-inclinao da equao de uma reta, temos:
(1) = 3 [ (1)]
y =3x + 2.
=

( + ) ( )

( + )

( + )

( )

5 - Encontre a equao da reta normal curva y = 3 que seja paralela reta 6x + 3y 4

= 0.
Soluo:
Seja a reta dada. Para encontrarmos a declividade de, escrevermos sua equao na forma
+

reduzida, que y =

. Portanto, a declividade de

2, e a declividade da reta

normal procurada tambm 2, pois suas retas so paralelas.

Para encontrarmos a declividade da reta tangente curva dada em qualquer ( ,
aplicamos a frmula
(

( ) = lim

),

+ ) ( )

Com f(x) = 3 obtemos

+ 3

( ) = lim

Para calcularmos esse limite, racionalizamos o numerador.

+ 3

( ) = lim

( ) = lim

3 (
+ 3+

+ 3+

+ 3+

3)

3)

Dividindo numerador e denominador por , desde 0, obtemos

1

( ) = lim

( )=

+ 3+
1

Conforme mostramos acima, a declividade da reta procurada -2. Assim, resolvemos

a equao 2
3 = -2 resultando
= 4. Portanto, A reta procurada a reta que passa
pelo ponto (4, 1) sobre a curva e tem uma declividade 2. Usando a forma ponto-declividade
da equao da reta obtemos y 1 = 2(x4) ou 2x + y 9 = 0.
Veja a figura 2.4, que mostra um esboo da curva junto com a reta normal PN em (4,
1) e a reta tangente PT em (4,1).

N
y

T
90
P(4,1)

Figura 2.4 Grfico da Reta Normal a curva

= 3.

6 - Calcule a derivada de ( ) = e use o resultado para determinar a equao da reta

tangente curva y = no ponto x = 4.
Soluo:
A derivada de

= em relao x dada por:

= lim

( + ) ( )
+
= lim

= lim

+ ( + + )
( + + )

= lim

= lim

+
( + + )
1
++

= lim

1
2

( + + )

Para x = 4, a coordenada correspondente y no grfico de y = y = 4 = 2; ento,

o ponto de tangncia P(4, 2). Como f(x) = 1/2 , a inclinao da reta tangente curva de
f(x) no ponto P (4, 2) dado por f(4) =

. Usando a forma ponto-inclinao da

equao de uma reta, descobrimos que a equao da reta tangente no ponto

P

2 = ( 4) ou

+ 1.

7 - Seja ( ) = ( ) = . Calcule f(2).

Soluo:
(

2) = lim

( ) (2)
2
= lim

2
2

Assim,
(

2) = lim

1
1
2
= lim
=

+ 2
22
2 ( + 2)

Isto ,
(

2) =

1
22

3. Regras de Derivao.
3.1. Derivada da Funo Constante.
Se c um nmero constante e a funo constante definida por ( ) = , ento f
diferencivel para todo nmero e a funo definida por ( ) = 0.
Prova:
(

) = lim

( + ) ( )

= lim
= lim 0 = 0.

Exemplos.
1 - Seja f uma funo constante definida pela equao ( ) = 5 +

. Calcule .

Soluo:
Pela regra da Constante, a funo definida pela equao ( ) = 0.

2 - Calcule

5 + 3 .

Soluo:
Pela regra da Constante,

(5 + 3) = 0.

10

3.2. Derivada da Funo Potncia.

Seja n um nmero inteiro maior que 1 e seja f a funo definida por ( ) =
f diferencivel para todo nmero e a funo definida por
(

)=

. Ento

Prova:
A prova se processa por induo matemtica, iniciando com n = 2. Para n = 2 temos, pelas
regras do produto e da identidade,
(

)=

(
(

)=
)=

( . ) = .(
+

=2 =2

)+(

Assim o teorema vlido quando n = 2. Agora, assumindo que n maior que 2 e que
o teorema seja vlido para expoentes menores que n, os Teoremas 4 e 2 implicam que
(

)=

)=

)=

. )=

+ [( 1)

( )=

].

.(
=

)+(
+ ( 1)

Exemplos.
1 - Seja ( ) = 4

encontre ( ).

Soluo:
( )=4
( )=4.
( )=

8
3

8
3

2 - Seja ( ) = 2

8
3

4 + 5, encontre h(x).

Soluo:
( ) = (2

4 + 5)

1
( ) = (2
2
( )=

4 + 5) (6
3

2
4 +5

4)

).

11

3.3. Derivada da Soma.

Sejam f e g funes diferenciveis em um nmero x, e seja h = f + g. Ento h
diferencivel em e
( )=

( )+

( ).

Prova:
(

( ) = lim

+ ) ( )

) = lim

) = lim

) = lim

) = lim

[ (

+ )+ (

+ ) ( )+ (

+ ) ( )

+ ) ( ) g(x + x) g(x )
+

( )=

+ )] [ ( ) + ( )]

+ ) ( )
+ lim

( )+

+ ) ( )

( ).

Exemplos.
1 - Seja ( ) = 3

+8x+5. Calcule a derivada.

Soluo:
( ) = 3(4

) + 8.1 + 0

( ) = 12

+ 8.

2 Seja ( ) = 7

( ).

+ 8 + 5,

Soluo:
( )=
= 28

(7
6

2
+8.

+ 8 + 5) =

(7

)+

(2

)+

(8 ) +

( 5) =

12

3.5. Derivada da Funo Produto.

Sejam f e g funes ambas diferenciveis em um nmero
tambm diferencivel em e
( ) = ( ).

( )+

, e seja =

g. Ento h

( ). ( ).

Prova:
(

( ) = lim

+ ) ( )

( ) = lim

+ ). (

+ ) ( ). ( ).

Usaremos agora um curioso, mas eficiente artifcio algbrico a expresso

( + ). ( ) subtrada do numerador e depois adicionada de novo (o que, claro,
mantm o valor do numerador sem alterao).

O resultado

( )=
(
= lim

+ ). (

+ ) (

) = lim

( ) = lim

+ ). ( ) + (

+ ) ( + ). ( )

f(x + x). g(x ) f(x ). g(x )

+
x
(

( ) = lim

+ ). (

+ )

+ ) ( ) f(x + x) f(x )
+
g(x )

+ ) lim

g(x + x) g(x )
f(x + x) f(x )
+ lim

x
x

lim g(x )

) = lim (

+ ). ( ) ( ). ( )

+ ) .

( )+

( )

lim

( )

13

Desde que, f diferencivel em

ela contnua em

Assim,
lim (

+ ) = lim ( ) = ( )

Tambm desde que g( ) uma constante,

( )= ( )

lim

Segue que,
( ) = ( ). g (x ) + f (x ). g(x ).

Exemplos.
[(3

1 - Calcule

+ 1)(7

+ )] pelo uso da regra da multiplicao.

Soluo:
[(3

+ 1)(7

+ )] = (3

= (3

+ 1)(21

= (63

+ 24

+ 1) + (42

= 105

+ 30

+ 1.

+ 1)[

+ 1) + (6 )(7
+6

(7

+ )] + [

(3

+ 1)](7

+ )

+ )
)

2 - Suponha que f e g so funes diferenciveis no nmero 2 e que f (2) = 1, g(2) = 10, f(2)
= e g(2) = 3. Se h= f . g, calcule h (2).
Soluo:
(

( ).

( )+

Ento:
(2) = (2).
Ou

( ). ( )

(2) +

(2) = (1)(3) +

(2). (2)

(10) = 8.

14

3.4. Derivada do Quociente.

e suponha que ( ) 0.

Sejam f e g funes ambas diferenciveis em um numero

Ento, se =

segue que h diferencivel em

( ).

( )=

( ) ( ).
[( )]

( )

Prova:
Note que h = f(1/g); assim pelas regras do produto e da inversa aritmtica,
( ) = ( ).
( )=

( )
+
[ ( )]

( ). ( )
+
[ ( )]

( ) =

( ).

1
( )

( ).

( ). ( )
[ ( )]

( ) ( ).
[ ( )]

( )
.

Exemplos.
1 - Sendo ( ) =

Calcule ( ).

Soluo:
( )=
( )=

5 + 3). (2.4 0) (2 3)(2 5)

( 5 + 3)
5 + 3)(8 ) (2 3)(2 5)

( 5 + 3)

(
(

2 - Calcule ( ) da funo

Soluo:
( )=

( )=

( )=

)(

2 (

+ 7) (
( + 7)
+ 7) (3
( + 7)

14

( + 7)

+ 7)

15

4. Derivada da funo composta (Regra da Cadeia).

Suponhamos que = ( + 5 ) e que desejamos determinar dy/dx. Uma sada
expandir ( + 5 ) e ento diferenciarmos o polinmio resultante.
Assim,
=(

+5 ) =

+ 15

+ 75

+ 125

=6

, ento

+ 75

+ 300

+ 375

Outro mtodo fazermos,

=

+ 5 , tal que

, dy/Du = 3

, du/dx = 2 + 5 .

Ento,
=

=3

(2 + 5) = 3(

+ 5 ) (2 + 5) = 6

+ 75

+ 300

+ 375

O ltimo clculo produziu a resposta certa, mas existe um detalhe nele. As expresses
so apenas smbolos para as derivadas nas quais os numeradores e denominadores
ainda no tiveram nenhum significado quando vistos separadamente, logo no estvamos
realmente seguros em supor que

. De fato, a legitimidade desse clculo garantida

por uma das mais importantes regras de diferenciao em clculo a regra da cadeia.

4.1 - A regra da cadeia.

Se y uma funo diferencivel de u e se u uma funo diferenvel de x, ento y
uma funo diferencivel de x e
=

claro, a regra da cadeia pode ser escrita na notao de operador como

=(

)(

).

Se fizermos y = f(u), onde u uma funo de x, faremos

( )=

( )

16

Exemplos.
(

1 - Calcule

+5 )

Soluo:
Aqui
(

+ 5 e n = 100, assim

+5 )

= 100(

2 - Se ( ) =

+5 )

+ 5 ) = 100(

+ 5 ) (2 + 5).

( ).

, calcule

Soluo:
Aqui ( ) = (3 1) , ento
( )=

( )=

(3 1)

= (4)(3 1)

( ) = (4)(3 1) (3) = 12(3 1)

3 - Calcule

(3 1)

Soluo:
3
+7

= 10

3
+7

3
+7

= 10

3
+7

3
+7

4 - Calcule

3
+7
(

(3 ) (210 30
( + 7)

( )

( ) = (2

+ 7)(3) (3 )(2 )
( + 7)
)

5 + 1) .

Soluo:
( ) = 7(2

5 + 1) (4 5) =

35 28

(2 5 + 1)

17

[(

5 - Calcule

+ 6 ) (1 3 ) ].

Soluo:
[(

+ 6 ) (1 3 ) ] = [

[(

+ 6 ) (1 3 ) ] = [10(
+(

+ 6 ) ](1 3 ) + (

+6 ) [

(1 3 ) ]

+ 6 ) (2 + 6)](1 3 ) +
+ 6 ) [4(1 3 ) (3)]

[(

+ 6 ) (1 3 ) ] = (

+ 6 ) (1 3 ) [10(2 + 6)(1 3 ) 12(

[(

+ 6 ) (1 3 ) ] = (

+ 6 ) (1 3 ) (72

+ 6 )]

232 + 60).

No clculo de derivadas algumas vezes necessrio usar a regra da cadeia

repetidamente. Por exemplo, se y uma funo de v, v uma funo de u, e u funo de x,

Ento,
=

6 - Seja

=( 1+

, e da

) . Use o fato de que

e a regra da cadeia para determinar

.
Soluo:
Seja

=1+

, tal que

= ( ) = (1 +

) .

Assim,
=
7 - Calcule

= (3

1
2

[1 + (1 +

(2 ) = 3( )

=3 =3

) ] .

Soluo:
Usando a regra da cadeia repetidamente, temos
[1 + (1 +

) ] = 7[1 + (1 +

) ]

[1 + (1 +

) ] = 7[1 + (1 +

) ] [6(1 +

[1 + (1 +

) ] = 7[1 + (1 +

) ] 6(1 +

) (5

[1 + (1 +

) ] = 210

[1 + (1 +

[1 + (1 +

) ] (1 +

) ]
(1 +

) .

)]

1+

18

A regra da cadeia realmente uma regra para a diferenciao da composta f g de

duas funes. Para ver isso, seja y = f(u) e u = g(x), tal que = ( ) = [ ( )] =
( )( ).

Desta forma, pela regra da cadeia,

( ) ( ) = [ ( )] ( ).

Denotando a composta f g por h, podemos escrever a regra da cadeia como a seguir:

Se h = f g, ento h(x) = (f g)(x) = f[ ( )] ( ).

Aqui, claro, estamos assumindo que g diferencivel no nmero x e f diferencivel

no nmero g(x).
8 - Seja ( ) = 4

+ 2 , ( ) =

. Calcule (f g) (x).

Soluo:
( )=4

( )=2

+ 1 ; assim, pela regra da cadeia

( )( )=

[ ( )] ( ) = 4[ ( )]

( )( )=4

1
4

2
3

( )

2 .

5. Derivada da Funo Inversa.

Seja = ( ) uma funo que admite inversa
seja,
( )= ,
Aplicando a regra da cadeia, temos
(

)( )=

1
( )

)( )=

( )

Portanto,

Desde que

( ) 0.

( ). Como

, ou

19

Exemplos.
1 Seja = ( ) = 5 . Obtenha (
regra da derivada inversa.

) (40) ( ) invertendo a funo, e ( ) utilizando a

Soluo:
=5

(a)

( )=

Logo,
(

)( )=

1
3 5

1
1
. =
5 15 5

Portanto,
= 40

(b)
(

) (40) =

2 Seja ( ) =

=5

( ) = 15

= 2. Como

, usando a regra da funo teremos

1
1
=

(2) 60

para

> 0. Determine (

) ( ).

Soluo:
J que definida e diferenciavl no intervalo aberto (0, ), e como ( ) = 2 0
para todos os valores de
no intervalo, segue do teorema da funo inversa que

inversivl,
diferencivel e
(
Vlido para todo
( ) = . Ento (

)( )=

no domnio de
)( )=

( )

( )

1
2

( )

. Desde que ( ) =

simplismente significa que

para
=

> 0, segue que

20

6. Derivada da Funo Exponencial.

6.1. Derivada da Funo Exponencial Composta.
Exemplos.
1 - Determine a derivada da funo ( ) =

Soluo:
De acordo com a regra do quociente,
( )=(

+ 1)(3

) (2 )

3( + 1) 2
( 1)

( )=

(2 )
3 2 3

( + 1)

2 - Determine a derivada da funo ( ) =

Soluo:
De acordo com a regra da cadeia,

( )=

3 - Determine a derivada da funo ( ) =

+ 1) = 2

Soluo:
De acordo com a regra do produto,
( )=

)+

( ) = (2

)+

(1) = (2 + 1)

6.2. Derivada da Funo Exponencial Logartmica.

Exemplos.
1 - Determine a derivada da funo

( ) = ln .

Soluo:
Combinando a regra do produto com a expresso da derivada de ln x, temos
( )=

1
+ ln
2

= 1 + ln .

21

2 - Determine a derivada da funo.

( )=

Soluo:
Como

, temos, de acordo com a regra da potncia para logaritmos

( )=

2
=3

Aplicando a regra do quociente para derivadas, obtemos:

3
2

( )=

2
( )=
3

) (
( )
1

2 14
3

( )=

3 - Determine a derivada da funo ( ) = ( + ln ) .

Soluo:

( )=

A funo tem forma

derivadas, obtemos:

, onde u = t + ln t aplicando a regra da potncia para

3
2

( )=

( )=

= ( +

( )=

) aplicando a regra da potncia para derivadas, obtemos:

3
2

( )=

3
( +
2

( )=

3
( +
2

( +
1+

)
.

22

7. Derivada das Funes trigonomtricas.

Antes de calcular as derivadas das funes trigonomtricas, observemos que
lim

cos 1

lim

cos 1

cos 1

(cos + 1)

= lim

= 1

0
1+1

cos 1

lim

= lim

lim

1
(cos + 1)

lim

= lim

cos 1

cos + 1

= 0.

7.1. Derivada da Funo Seno.

O quociente de Newton da funo sen x
( + )

Para calcular seu limite, desenvolvemos sen (x+h) usando a frmula do seno da soma
de dois arcos.
Ento temos,

( + )

= lim

( + )

= lim

( + )

= lim

( + )

( + )

= cos .

Logo,
(

) = cos .

cos +

. cos

(cos 1) + sen

cos 1
+

0+1

cos

23

Exemplos.
=

1 - Determine a derivada da funo

=

Soluo:
=

).

= cos . 2
= 2 . cos(

).

( )

2 Determine a derivada da funo

( )

Soluo:
(

( ) =

(3

( ) =

+
+

( ) =
( ) =

3 Calcule a derivada da funo h(x) =

h(x )= (

(3 ) + 3

h(x) = 3
h(x) = 3

(3 ) +

(3 )]
(3 )

(3 ) + cos (3 )].

7.2. Derivada da Funo Cosseno.

Se y = cos x, ento y = sen x.
Prova:
Seja y =
= lim

aplicando a definio
cos( + ) cos

(3 ).

24

aplicaremos a frmula trigonomtrica:

Cos p cos q = 2 sen

. sen

Ento,

= lim

+ +
.
2

2 +
2

y = lim 2

/2

2. 2

. lim

1
. .1
2

= 2.
=

+
2

Exemplos.
= cos (1/x).

1 - Determinar a derivada da funo

=

Soluo:

y= cos u, u = (1/x)
y = ( sen u ) . u
y = [
y =

(1/ )]. 1/

sen (1/x).

2 Determinar a derivada da funo

= cos (1/x).

Soluo:
y= cos u, u = (1/x)
y = ( sen u ) . u
y = [
y =

(1/ )]. 1/

sen (1/x).

25

( ). ( ) , no ponto

=2

3 - Determine a derivada da funo

Soluo:
( ) = 2 cos( ) .

( ) = 2[(cos ( )) .

+ cos( ) . (

( )=2

+ cos( ) .

( ).

( ) = 2

( )+

( ) = 2

( )+

( ) =2 0+

1
1

. cos ( )
. cos ( )

7.3. Derivada da Funo Tangente.

Usando a relao t g =
(

) =

) =

) =

) =

) =

1
.

Logo,
(

) =

obtemos

. (

)]

= .

26

Exemplos.
1 Calcule a derivada da funo ( ) =

( )

Soluo:
(

( )=

( )=

2 ). (5

2) .
(

(5

2)

2 Calcule

(
(
=

se

2 )

)
2 )
)

2 )

4 .

Soluo:
Como

4 =(

= 3(

4 ) , a regra da potncia d

4 )

4 .
=4 ,

Pela frmula (1) com

4 =(

4 )(4),

E, juntando os vrios pedaos, obtemos

= 12

4 .

7.4. Derivada da Funo Cotangente.

=

Usando a relao
Obtemos,
. (

) =

) =

) =

) =

1
.

Logo,

) =

27

Exemplos.

1 - Calcule

(1 3 ).

se =

Soluo:
Pela frmula
=
com

= 13 ,
(1 3 ). (3) = 3

(1 3 ).

7.5. Derivada da Funo Secante.

A partir de sec

obtemos

. 0 1 . (

) =

) =

) =

) =

) =

Logo,
(

Exemplos.
1 - Determinar a derivada da funo

= sec (

+ 3 + 7).

Soluo:
=

=
= [

=
.

= (2 + 3)

+3 +7
.

+ 3 + 7) .
(

+ 3 + 7)]. (2 + 3)

+ 3 + 7).

+ 3 + 7)

28

7.6. Derivada da Funo Cossecante.

De

vem,

.0 1 .

) =

) =

) =

) =

1
.

Logo,
(

) =

Exemplos
=

1 - Dada a funo

. Calcule sua derivada.

Soluo:
=

.
+1
.
1

=
=

+1
.
1

2
.
( 1)

2 Dada

+1
1
+1
.
1

(6 ). Calcule

=4

2
( 1)
+1
.
1

Soluo:
= 4. (
= 24

(6 ).
(6 ).

(6 ). (6))
(6 ).

29

8. Derivada das Funes trigonomtricas Inversas.

8.1. Derivada arc seno.
A funo arc seno , a inversa da funo seno. Para que a funo seno se tornasse
inversvel, tomamos o intervalo

para seu domnio e [1 , 1] para contradomnio.

Assim a funo arc seno x a inversa da funo f :

[1 , 1] dada por y = f (x) =

sen x.
Usemos ento, a letra y para indicar a varivel da inversa de f que a funo g(y) = arc
seno .
Assim, desde que ( ) =

, temos

1
( )

( )=
( )=

0 ,ou seja ,

1
cos

Como

, temos cos

= 1

> 0 , o que exige cos

devemos ter

. Sabendo que

. Conseqentemente ( ) =

ou
(

) =

. Usando novamente a letra x para representar a varivel da funo

arco-seno, temos
(

)=

Exemplos.
1 Dada

encontre

Soluo:
Aplicando a frmula

)=
=

, obtemos

1
1(

(2 ) =

2
1

30

8.2. Derivada arc cosseno.

Relembrando: a funo f: [0,

] [1 , 1] dada por y = f(x) = cos x a inversa da

funo
g(y) = arc cos y.

Logo,
desde que f(x) = sem x 0 , ou seja , x (0 , ),

Temos,
1
( )

( ) =
( )=

Como
=

, temos

, e sabendo que

[0 , ] , temos,

.
( )=

Assim,

= 1

, ou (arc cos y)=

E usando novamente a letra x para indicar a varivel da funo arc cos, temos
(arc cos x) =

Exemplos.
1 Dada ( ) =

, encontre

Soluo:
( )=
=
=

1
1

2 . 1
1
2

1
2

31

8.3. Derivada arc tangente.

Como a funo f:

dada por y = f(x) = tg x a inversa de g(y) = acr tg y ,

temos,
( ) =
( ) =

1
( )
1

. Como

Temos,
=1+
=1+

Logo,
( ) =

, ou (

) =

) =

, ou , ainda ,(arc

Exemplos.
1 Dada ln( + ) =

encontre

Soluo:
Derivando, implicitamente, os dois membros da equao dada em relao a , obtemos

1
(1 +
+

1+

Ou
1+
+

Ou
+

+(

Ou
=

2 +

32

8.4. Derivada arc cotangente.

: (0 , ) dada por

A funo
.

( ) =

a inversa de

Logo,
1
( )

( ) =
( ) =

De

= 1+

, vem

Portanto,
( ) =
(

ou (

) =

1
1+

) =

ou, ainda,

encontre

Exemplos.
1 Dada

Soluo:
= 3

1
+
3

=3

1
3

3
9+

1
1
1+
9

1
3

8.5. Derivada arc secante.

Como

, temos

Logo,
(

) =

) =

1
1
1

( ) =

33

) =

1
(

) =

) =

) =

1
1
1

1
| |
1

| |.

8.6 Derivada arc cossecante.

=

Como

, temos a

Assim,
(

) =

) =

1
1
1

) =

) =

) =

1
1

1
1

1
| |
1

| | .

34

9. Derivadas Sucessivas ou de Ordem Superior.

De um modo geral, se uma funo diferencivel em algum intervalo aberto, ento a
derivada de
novamente uma funo definida neste intervalo aberto e podemos perguntar
se diferencivel no intervalo. Se o for, ento sua derivada( ) escrita, por simplicidade,
como "(leia-se duas linhas). Denominamos " de derivada de segunda ordem, ou
simplesmente de derivada segunda da funo . Por exemplo, se uma partcula se move ao
longo de uma reta orientada de acordo com a lei de movimentos = ( ), ento
so
representados na notao simplificada.
=

( ),

( ) = "( ).

No existe nada que prove, ao se tomar, sucessivamente, derivadas de uma funo

tantas vezes quantas forem necessrias, que as funes derivadas permaneam diferenciveis
em cada estagio. Desta forma, se
e uma funo e se ,
"so diferenciveis num
intervalo aberto, ns podemos formar a derivada de terceira ordem, ou derivada terceira,
=
( ) ; se,
tambem diferencivel no intervalo, podemos obter a derivada de quarta
ordem, ou derivada qurta,
= ( ) , e assim por diante. Se pode ser sucessivamente
diferenciavel vezes desta forma, dizemos que vezes diferencivel.
Visto que

( )

e uma funo constante,todas as derivadas subseqentes so nulas,

isto ,
( )(

)=0

para

5.

Assim como para a derivada primeira, ns freqentemente ignoramos deliberadamente

a distino entre a funo derivada de ordem -sima ( ) ( )e o valor desta funo ( ) no
ponto x, e ambas so referidas como a -sima derivada.
A notao operacional para derivadas de ordem superior auto-explicativa; sem
dvida, D
( ) significa ( ) ( ). A correspondente notao de Leibniz induzida como se
segue: Se = ( ) tal que

( )=

( ),

Ento a segunda derivada dada por

( )=

O smbolo

( ).

para a derivada segunda incmodo. O tratamento algbrico

formal, como se fosse frao real, converte-se

em (

. Os parnteses do denominador

so, na prtica, omitidos, e a derivada segunda escrita como

. Notao anloga

empregada no das derivadas de ordem superior com se constata pela tabela 1.

35

= ( )

Notao simplificada
=

1. derivada
primeira

Operador

Leibniz

( )

( )
=

( ) =

2. derivada
segunda

3. derivada
terceira

) =

( )

( )

)=

)=

( )

.derivada
-sima

( )

( )

( )

( )

( )

( )

( )

)=

( )
=

( )

Tabela 9.1 Tabela de derivadas de ordem .

Exemplos.
1 encontre todas as derivadas de ordem superior da funo polinomial
8 + 3 2 + 4.
Soluo:
( ) = 60
( ) = 180

24

+ 6 2,

48 + 6,

( ) = 360 48,
( )=
( )=

( )=
( )=

( )

( ) = 360,

( ) = 0.

( ) = 15

36

= 2

2 Se

, ache:

(a)

(b)

(c)

Soluo:
(a)

(b)

(c)

4+

3 Seja ( ) =

=4 +
=

. Ache:

(0).

(a)

=4

(b)

(1).

Soluo:
( )=

(3 + 2)(2) (2 1)(3)
7
=

(3 + 2)
(3 + 2)

e
( )=

7
(3 + 2)

=7

[(3 + 2) ] = 14(3 + 2)

Portanto,
( ) (0) =

7
7
=
[3(0) + 2]
4

( )

(1) =

42
42
=
[3(1) + 2]
125

( )

(0) =

42
42
21
=
=

[3(0) + 2]
8
4

( 3 + 2) =

42

( 3 + 2)

37

10. Diferenciao Implcita.

Exemplos.
1 Dada ( + ) ( + ) =

encontre

Soluo:
Diferenciando implicitamente em relao a , temos 2( + )(2 + 2 )
(2 2 )
= 4 +4
do qual obtemos,
2 + 2 + (2 + 2 )
(4 4

)=4

2 + 2 + (2 2 )

=4

2 +2 +

+4

2 Encontre a equao da reta tangente curva

= 9 no ponto (1, 2).

Soluo:
Diferenciando implicitamente em relao a , obtemos 3

+3

=0

Portando,
=
Portanto, no ponto (1, 2),

= . Ento a equao da reta tangente :

1
2 = ( 1)
4

3 Dada a equao
+
= 9, encontre: (a)
por diferenciao implcita; (b) duas
funes definidas pela equao; (c) a derivada de cada uma das funes obtidas na parte (b)
por diferenciao implcita; (d) verifique se o resultado obtido na parte (a) concorda com os
resultados obtidos na parte (c).
Soluo:
(1) Diferenciando implicitamente, encontramos 2 + 2
(2) Resolvendo a equao dada para , obtemos
= 9

= 9

= 0 e assim

38

Seja

a funo para a qual

( )=

a funo para a qual ( ) = 9

(3) Como

( ) = (9

) usando a regra da cadeia obtemos

1
( ) = (9
2

(2 ) =

Analogamente, obtemos
( )=

(4) Para

( ) onde

( ) = 9

, temos da parte (3)

( )=

Que coerente com a resposta n aparte (1). Para

da parte (3)
( )=

Que tambm est de acordo com a resposta (1).

( ), onde

( ) = 9

, temos

39

11. Teorema de L`Hospital.

As regras de L`Hospital, que vamos enunciar a seguir, aplicam-se a clculos de limite
que apresentam indeterminaes do tipo

11.1 - 1 Regra de L`Hospital:

Sejam e derivaveis em ]p - r , p[ e em ]p , p + r[ ( r > 0), com g`(x) 0 para 0 < I
x - p I < r. Nestas condies, se

lim ( ) = 0, lim

lim

( )
( )
existir( inito ou in inito), ento lim
existir e
( )

( )

lim

( ) = 0.

( )
( )

lim

( )

( )

Observamos que a primeira regra de L`Hospital continua valida se substituirmos x

ou x
ou x .

11.2- 2 Rregra de L`Hospital:

Sejam e

derivveis em ] m, p [ , com g (x) 0 em ] m, p [ . Nestas condies, se

lim

lim

( ) = + ,

lim

( )
existir ( inito ou in inito) ento lim

( )

lim

( )
= lim

( )

( ) = +

( )
existir e
( )
( )

( )

Observamos que a 2 regra de L`Hospital continua vlida se substituirmos

por ou por xp ou por x . A regra permanece vlida se substituirmos

um dos smbolos +, ou -.

40

Exemplos.

Calcule lim

+ 8
1

Soluo:
6

lim

+ 8
1

0
.
0

Temos,
lim

6
(

+ 8 3)
5
= lim

1)

18
4

+ 8

Pela 1 regra de L`Hospital

lim

+8 3
(
= lim

6
(

+ 8 3)
5
=
1)
4

Ou seja,
lim

+8 3
5
=
1
4

calcule lim

Soluo:
Pela 2 regra de L`Hospital,
lim

= lim

Assim,
lim

= + .

( )
= lim
( )

= + .

41

Calcule lim

ln

= [0 . ()].

Soluo:
Note que uma indeterminao que poder ser colocada na forma
interessante aqui pass-la para a forma
lim

ln

ln
lim
1

= lim

ln

=
.
1

1
(ln )
= lim
= lim
= lim ( ) = 0
1
1

Ou seja,
lim

, que nos permitir eliminar o ln x.

ln = 0 .

ou

mais

42

12. Diferencial.
At ento, a derivada

= ( ) foi vista como uma simples

de uma funo real

notao. Interpretaremos, a partir da definio de diferencial, a derivada como um quociente

de acrscimo.
12.1 - [Acrscimos e decrescimento] Um acrscimo (decrscimo) feito a um valor x se
somarmos (subtrairmos) um valor .
12.2 [Diferencial da varivel Independente] Seja = ( ) uma funo derivvel. O
diferencial de , denotado por , o valor do acrscimo , isto ,
= .
12.3 [Diferencial de Varivel Independente] O diferencial de , denotado por
acrscimo na ordenada da rgua tangente , correspondente ao acrscimo
em .

Figura 12.1 Interpretao Geomtrica da Derivada

Considere a reta tangente ao grfico da funo
de inclinao de .

= ( ) no ponto . Seja

De acordo com a figura 12.1, podemos observar que

, o

( ). Mas,

o ngulo

( )=

( ), pois esta a interpretao geomtrica da derivada. Logo,

=

( ).

O acrscimo
pode ser visto como uma aproximao para . Esta aproximao
tanto melhor quanto for o valor de
0, ento
0.
Segue que podemos considerar
= ( + ) ( ),
( +

se
for suficientemente pequeno. Como
( + ) ( ) . Segue que
) ( )+

( )

43

Exemplos.
1 Encontre aproximadamente o volume de uma concha esfrica cujo raio interior 4 cm e
cuja espessura

cm.

Soluo:
Consideremos o volume da concha esfrica como o incremento do volume de uma esfera.
Sejam,
= Ao nmero de centmetros no raio de uma esfera;
= Ao nmero de centmetros cbicos no volume de uma esfera;
= Ao nmero de centmetros cbicos de uma concha esfrica.
=

4
3

Logo,
=4
Substituindo

=4

nas expresses anteriores, Obtemos

= 4 ( 4)

1
=4
16

Portanto,
V 4, e conclumos que o volume da concha esfrica aproximadamente 4 cm .
2 o raio de uma esfera de ao mede 1,5 centmetros e sabe-se que o erro cometido na sua
medio no excede 0,1 centmetros. O volume da esfera e calculado a partir da medida de
seu raio usando-se a frmula = 4 3
. Estime o erro possvel no calculo de seu volume.
Soluo:
O valor real do raio 1,5 + , onde o erro de medida. Sabemos que | | 0,1. o
valor verdadeiro o volume 4 3 (1,5 + ) , enquanto o valor do volume do raio calculado
medido 4 3 (1,5) . A diferena = 4 3 (1,5 + ) 4 3 (1,5) , representa o erro
no clculo do volume. Colocamos
= e estimamos por
como se segue. Observe
que
=
Conseqentemente,

4
3

=4

44

= 4 (1,5) = 9 .

=4

Portanto, | | |9 | = 9 | | 9 (0,1) = 0,9 , e ento o erro possvel

limitado em valor absoluto por cerca de 0,9 2,8
.
3 Use diferenciais para achar o volume aproximado de uma camada cilndrica circular de 6
cm de altura cujo raio interno mede 2 centmetros e cuja espessura e de 1 10

.
Soluo:
O volume de um cilindro circular reto igual sua altura vezes a sua rea da base. Se V
.
denota o volume de um cilindro (slido) de altura 6 centmetros e raio r, ento = 6
.A
diferena no volume desses dois cilindros o volume procurado da camada. Fazemos
=

e usamos a aproximao

(6

= 12

12
= 12 (2) 1 10 =
.
5
7,5 centmetros cbicos.

Assim, o volume da camada aproximadamente

13. Taxa de Variao.

Suponhamos que uma partcula se desloca sobre o eixo

com funo posio
= ( ). Isto significa dizer que a funo fornece a cada instante a posio ocupada pela
partcula na reta. A velocidade mdia da partcula entre os instantes e + definida pelo
quociente entre

( )

, onde = ( + ) ( ) o deslocamento da partcula no

instante e + . A velocidade da partcula no instante

(caso exista) de em , isto :
( )=

definida como sendo a derivada

( ).

Assim, pela definio de derivada,

( ) = lim

( + ) ( )

A acelerao no instante definida como sendo a derivada em da funo ( ) =

Pela definio de derivada,
( ) = lim

O quociente

( )

( + ) ( )

a acelerao mdia entre os instantes

+ .

45

Exemplos.

1 Uma escada de 5 metros de altura est apoiada numa parede vertical. Se a base da escada
arrastada horizontalmente da parede a 3 m/seg, a que velocidade desliza a parte superior da
escada ao longo da parede, quando a base se encontre a 3 m da parede?

Soluo:
Seja,
= Ao nmero de segundos transcorridos desde que a escada comeou a deslizar na parede.
= Ao nmero de metros desde o piso at a parte superior da escada em t seg.
= Ao nmero de metros desde a base da escada parede em t seg.
Como a base da escada arrastada horizontalmente da parede a 3 m/seg.
encontrar
quando = 3.

= 3. Queremos

Do teorema de Pitgoras, temos

= 25

(1)

Como
e obtemos

so funes de , derivamos ambos os membros da eq. (1) em relao a

= 2

Dando-nos
=

(2)

Quando
]

= 3, segue da eq. (1) que

= 4. Como

= 3, temos de (2)

3
9
3=
4
4

Portanto, a parte superior da escada est deslizando na parede taxa de 2

m/seg,

quando a base est a 3 m da parede. ( O significado do sinal menos que decresce quando
cresce.

46

2 Dois carros, um dirigindo-se para o leste taxa de 72 km/h e o outro para o sul taxa de
54 km/h esto viajando em direo ao cruzamento de duas rodovias. A que taxa os carros se
aproximam um do outro, no instante em que o primeiro estiver a 400 m e o segundo estiver a
300 m do cruzamento?
Soluo:
Seja,
= Ao nmero de metros que o primeiro carro est distante de P em seg.
= Ao nmero de metros que o segundo carro est distante de P em seg.
= Ao nmero de metros que indica a distancia entre os dois carros em
Desde que o primeiro carro se aproxima de P taxa de72km/h = 72
que

decresce quando t cresce, temo0s conseqentemente

54 km/h = 54

quando

= 20m/seg e

= 20. Analogamente, como

= 15.

m/s = 15 m/s,

Queremos encontrar

= 400

= 300.

Do teorema de Pitgoras, temos

=

(3)

Derivando os dois membros da eq. (3) em relao a t, obtemos

2

=2

+2

E assim,
=

Quando
substituindo-se
]

(4)

= 400
= 300, com base na eq. (3) temos que = 500. na eq. (4)
= 20,
= 15, = 400, = 300
= 500 obtemos

(400)(20) + (300)(15)
= 25.
500

Portanto, no instante em questo os carros aproximam-se um do outro taxa de -25

m/seg.

47

3 Um empresrio calcula que quando unidades de um certo produto so fabricadas,a

receita bruta associada ao produto dada por ( ) = 0,5
+ 3 - 2 milhares de reais.qual
a taxa de variao da receita com o nvel de produo
quando 3 unidades esto sendo
fabricadas? Para esse nvel de produo, a receita aumenta ou diminui com o aumento da
produo?
Soluo:
Como representa o numero de unidades fabricadas, temos necessariamente
quociente diferena de ( )

0. O

( + ) ( )
=

=
=

[0,5(

+ 2 + ) + 3( + ) 2] [0,5

+ 0.5 + 3
=

+ 3 2]

+ 0,5 + 3.

14 Intervalos de Crescimento e Decrescimento.

14.1 Teorema.
Seja
(a, b).
(i)
(ii)

uma funo definida no intervalo fechado [a, b] e derivvel no intervalo aberto

Se
Se

( ) > 0, para todo ( , ), ento crescente em [ , ];

( ) > 0, para todo ( , ), ento decrescente em [ , ];

Em ambos os casos

dita montona.

14.2 Interpretao geomtrica.

Observe na figura 14.1, que quando a inclinao da reta tangente for positiva, a funo
ser crescente e quando a inclinao da reta for negativa, a funo ser decrescente. Como
( ) a inclinao da reta tangente curva = ( ), crescente quando ( ) < 0.

Figura 14.1 Representao Grfica da inclinao da reta Tangente.

48

Exemplos.
1 A funo
;

( )=

crescente em , pois sua derivada

Figura 14.2 grfico da funo ( ) =

( )=3

0,

2 A funo ( ) = decrescente em qualquer intervalo que no contenha o zero, pois

sua derivada

( )=

< 0,

Figura 14.3 Grfico da funo ( ) =

15. Mximos e Mnimos.

Freqentemente nos interessamos por uma funo definida num dado intervalo e
queremos encontrar o maior ou o menor valor da funo no intervalo. Discutiremos esta
questo a seguir.

49

15.1 Definies:
Sejam :

uma funo e

. Dizemos que

ponto de:

15.1.1 Mximo relativo.

Se existir um intervalo aberto contendo

tal que

( ) ( ),

15.1.2 Mximo absoluto.

Se ( ) ( ),

15.1.3 Mnimo Relativo.

Se existir um intervalo aberto contendo

tal que

( ) ( ),

15.1.4 Mnimo absoluto.

Se ( ) ( ),

Figura 15.1 Grfico de uma Funo , contendo Mximo e Mnimo local.

A figura 15.1, mostra o esboo de parte do grfico de uma funo, tendo um valor mnimo
local em = e um valor mximo local em = .

Em geral, um ponto de mximo ou de mnimo chamado de ponto extremo.

50

Exemplos.
1 Dada ( ) = 2 encontre os extremos.
Soluo:
em [1,4).

A figura 15.1, apresenta um esboo do grfico de

A funo tem um valor mnimo absoluto de 2 em [1,4). No existe um valor

mximoabsoluto de em [1, 4), pois
lim ( ) = 8,

Mas ( ) sempre menor que 8 no intervalo dado.

Absolutos de

no intervalo [1, 4) se existirem.

y
8

Figura 15.2 grfico de

2 - Dada ( ) =

em [1,4).

encontre os extremos absolutos de

em (3, 2] se existirem.

Soluo:
A figura 15.3, mostra um esboo do grfico de

em (-3, 2].

A funo tem um valor mximo absoluto de 0 em (3, 2]. No existe valor mnimo
absoluto de em(3,2], pois
lim ( ) = 9,

mas ( ) sempre menor que 9 no intervalo dado.

y
-3

-4

-9

Figura 15.3 Grfico de

em (-3, 2]

51

3 - Dada ( ) =

+1
6 +7

<1
1

encontre os extremos absolutos de

em [5,4]

se existirem.
Soluo:
em [5, 4].

A figura 15.4, mostra um esboo do grfico de

O valor mximo absoluto de em [5,4] ocorre em 1 e (1) = 2; o valor mnimo absoluto

de em [5,4] ocorre em 5, e (5) = 4. Note que tem um valor mximo relativo em
1 e um valor mnimo relativo em 3. Note tambm que 1 um numero crtico de , pois
no existe em 1, e 3 um numero crtico de , pois (3) = 0.

Figura 15.4 Grfico da Funo

em [-5, 4]

4 - A funo ( ) = 3 12 tem um mximo relativo em

(2,2) tal que (0) ( ) para todo (2,2).

= 0, pois existe o intervalo

Em
= 2
= +2, a funo dada tem mnimos relativos, pois (2)
( ) para todo (2,0)
(2) ( ) para todo (0,2), conforme figura 15.5.
Y

-2 - 2

2
X

-12

Figura 15.5 Grfico da Funo ( ) = 3

12

52

15.2 Teorema de Weirstrass.

Se f for continua em [a, b], ento existiro
f( ) para todo x em [a,b].

em [a, b] tais que f( ) f(x)

Demonstrao:
Sendo f continua em [a, b], f ser limitada em [a, b], da o conjunto A = {f(x) / x
[a,b]} admitir supremo e nfimo.
Sejam,
M = Sup {f(x) / x [a, b]}.
m = Inf {f(x) / x [a, b]}.

Assim, para todo x em [a, b], m f(x) M.

Provaremos, a seguir, que M = f( ) para algum
para todo x em [a, b], a funo g(x) =

( )

em [a, b]. Se tivssemos f(x) < M

, x [a,b] ( veja observao na outra pgina).

Seria continua em [a, b], mas no limitada em [a, b] que uma contradio (Se g
fosse limitada em [a, b], ento existiria um > 0 tal que para todo x em [a, b]
0<=

( )

<

e, portanto, para todo x em [a, b],

f(x) < M E assim,
M no seria supremo de A).
Segue que f(x) < M para todo x em [a, b] no pode ocorrer, logo devemos ter M =
f( ) para algum em [a, b]. Com raciocnio anlogo, prova -se que f( ) = m para algum
, em [a, b].
Observao: A idia que nos levou a construir tal funo g foi a seguinte: Sendo M o
supremo dos f(x), por menor que seja r > 0, existir x tal que M r < f(x) < M; assim, a
diferena M f(x) poder se tornar to pequena quanto se queira e, portanto, g(x) poder se
tornar to grande quanto se queira.

53

15.3 Teorema de Fermat.

Seja : uma funo derivvel, um intervalo e
1.
2.
3.

Ento

tal que:

um ponto de mximo ou de mnimo local;

um dos extremos do intervalo , isto , se = [ , ], ento
derivvel em ;

( ) = 0.

15.3.1 Definio.
O ponto
pertencente ao domnio de
chamado de ponto crtico de .

tal que

( )=0

( ) no existe,

Portanto, uma condio necessria para a existncia de um extremo relativo em um ponto

que seja um ponto crtico de .

15.4 Teorema (Critrio da primeira derivada).

Seja [ , ] uma funo contnua e derivvel em (a, b) exceto possivelmente em
( , ).
I.
II.

Se ( ) > 0,
de .
Se ( ) < 0,
de .

<

( ) < 0,

> , ento c um ponto de mximo local

<

( ) > 0,

> , ento c um ponto de mnimo local

Esse teste estabelece essencialmente que se for contnua em c e ( ) mudar de sinal

positivo para negativo quando cresce atravs de c, ento ser um valor mximo relativo
em c, e se ( ) mudar o sinal de negativo para positivo enquanto x cresce atravs de c, ento
ter um valor mnimo relativo em c.
Observe a Figura 15.6, ela mostra que, numa vizinhana de um ponto c de mximo local,
as retas tangentes a curva passam de coeficiente angular positivo ( esquerda de c) para
negativo ( direita de c). E o coeficiente angular justamente a derivada de .
Enquanto que, na 15.7, temos uma vizinhana de um ponto c de mnimo local, onde as
retas tangentes curva passam de coeficiente angular negativo ( esquerda de c) para (
direita de c). Note que em ambos os casos ( ) existe e igual a zero.

54

Figura 15.6

Figura 15.7

Resumidamente, este teste estabelece essencialmente que se for contnua em c e

( ) mudar de sinal positivo para negativo quando cresce atravs de c, e se ( )
mudar o sinal de negativo para positivo enquanto cresce atravs de c, ento ter um
valor mnimo relativo em c.

Exemplos.
1 A funo ( ) = ( 2) , esboada na Figura 15.8, mostra, que mesmo tendo um
( ) > 0 quando > 2 ou seja, no tem um
ponto crtico, nesse caso em
=2
extremo relativo em 2.

Figura 15.8

55

2 A figura15.9, mostra um esboo de grfico de uma funo , que tem um valor mximo
relativo num nmero c mas ( ) no existe, contudo ( ) > 0 quando <
( )<0
quando > .

Figura 15.9
Em suma, para determinar os extremos relativos de :
(1) Ache ( );
(2) Ache os nmeros crticos de ( ), isto , os valores de
para os quais ( ) no existe;
(3) Aplique o teste da derivada primeira

para os quais

( ) = 0, ou

3 Dada ( ) =
12 + 9 + 1 ache os extremos relativos de , aplicando teste da
derivada primeira. Determine os valores de nos quais ocorrem extremos relativos, bem
como os intervalos nos quais crescente e aqueles onde decrescente. Faa um esboo
do grfico.
Soluo:
Temos que ( ) = 3 12 + 9 e ( ) existe para todos os valores de por se tratar
de um polinmio. Portanto, resolve-se a equao ( ) = 0, ou seja, 3 12 + 9 =
3( 3)( 1) = 0. Segue que: = 3
= 1 so nmeros crticos de . Pra determinar
se possui extremos relativos nesses nmeros, aplicaremos o teste da primeira derivada,
conforme o tabela 15.1, e Figura 15.10.

Tabela 15.1

Figura 15.10

56

15.5 outro teste para o clculo de mximos e mnimos.

Com o teste da primeira derivada, podemos determinar se uma funo tem valor
mximo ou mnimo relativo num nmero crtico c, verificando o sinal de em nmeros
contidos em intervalos direita e esquerda de c. Veremos a seguir, outro teste para extremos
relativos envolvendo somente o nmero crtico c.

15.5.1 critrio da segunda derivada.

Sejam : [ , ] uma funo contnua e derivvel at segunda ordem em
( , ), com derivadas
tambm contnuas em e c tal que ( ) = 0.

Ento,
(1) Se
(2) Se

( ) < 0, c ponto de mximo local;

( ) > 0, c ponto de mnimo lolcal.

Percebe-se, facilmente, nas Figuras, que exibiremos a seguir, que o teste falha quando
f (c) = 0, nada se pode concluir quanto aos extremos relativos. Deve-se, portanto, utilizar
somente o teste da derivada primeira.

Figura 15.11

Figura 15.12

Figura 15.13

Considerando as funes = , = e = , notemos que cada uma delas

possui a segunda derivada nula em = 0. Em = 0, a funo =
possui um mnimo
relativo, e = possui um mximo relativo, no entento, para y = x no tem mximo e
nem mnimo relativo.

57

15.6 Teorema de Lagrange.

Se [ , ] uma funo contnua em [a, b] e derivvel em (a, b), ento existe pelo
menos um ponto ( , ) tal que
( ) ( )
=

( ).

15.6.1 Interpretao geomtrica do Teorema de Lagrange.

Num esboo do grfico da funo , conforme Figura 15.14,

( )

( )

a inclinao do

segmento de reta que liga os pontos A( , ( )) e B( , ( )). O Teorema de Lagrange afirma

que existe um ponto sobre a curva entre A e B, onde a reta tangente paralela reta secante
( )=

por A e B, ou seja, existe um ( , ) tal que

( )

( )

( ).

Figura 15.14

16. Concavidade e ponto de inflexo.

Seja derivvel no intervalo e seja
grfico de
( )=

( )( ) ou

= ( )+

um ponto de . A reta tangente em ( , ( )) ao

( )( ).

Deste modo, a reta tangente em ( , ( )) o grfico da funo T dada por

( ) = ( )+

( )( ).

58

Definies.
1 Dizemos que tem a concavidade para cima no intervalo aberto , conforme as Figuras
16.1 e 16.2, se quaisquer que sejam e em , com .
y

Figura 16.1

2 Dizemos que

Figura 16.2

tem a concavidade para baixo no intervalo se

( ) < ( ).

Quaisquer que sejam

em , com

3 Sejam uma funo e , com contnua em . Dizemos que ponto de inflexo

de se existirem nmeros reais e , com ] , [ , tal que tenha concavidade de
nomes contrrios em ]a, p[ e em ]p, b[, como podemos perceber nas Figuras 16.3 e 16.4.
Y

f
p

Figura 16.3

Figura 16.4

59

Teorema.
Seja

uma funo que admita derivada at a 2 ordem no intervalo aberto .

(i)
(ii)

Se
Se

( ) > 0 em , ento
( ) < 0 em , ento

ter a concavidade voltada para cima em .

ter a concavidade voltada para baixo em I.

Exemplos.
1 Seja
inflexo.

( )=

. Estude

com relao concavidade e determine os pontos de

Soluo:
( )=
( )=(

Como

> 0 para todo , o sinal de

1)

( ) o mesmo que o de

Figura 16.5
( ) > 0 em ] , 1[ e em ]1, +[.
( ) < 0 em ] 1, 1[.
Ento, conforme a Figura 16.5,
tem a concavidade voltada para cima em ] , 1[ e em ]1, +[ ;
tem a concavidade voltada para baixo em ] 1,1[ ;
Pontos de inflexo: 1 1.

1.

60

2 Dada a funo de inida por ( ) =

6 + 9 + 1 ache o ponto de inflexo do
grfico de , caso tenha, e determine onde o grfico cncavo e convexo.
Soluo:
( ) = 6 12. ( ) existe, para todos valores
Temos que ( ) = 3 12 + 9 e
de . ( ) = 0 6 12 = 0 = 2. Para determinar se existe ou no um ponto de
inflexo em = 2, precisa verificar se ( ) muda de sinal; ao mesmo tempo, determinamos
a concavidade do grfico para respectivos intervalos, conforme Tabela 16.1 e Figura 16.6.

Tabela 16.1

Figura 16.6

3 Dada ( ) =
5 3 verifique que a hiptese do teorema do valor satisfeita
para = 1
= 3. Ento, encontre todos os nmeros no intervalo aberto (1,3) tais que
( )=

(3) (1)

31

Soluo:
Como uma funo polinomial, continua e derivvel para todos os valores de .
Portanto, a hiptese do teorema do valor mdio satisfeita para qualquer
.
( )=3
(1) = 7

10 3
(3) = 27

Logo,
(3) (1) 27 (7)
=
= 10.
31
2
Determinando

( ) = 10, obtemos
3

10 3 = 10

Ou
3

10 + 7 = 0

61

Ou
(3 7)( 1) = 0
Que resulta:
=

7
3

= 1.

Como 1 no pertence ao intervalo aberto (1,3), o nico valor possvel para

7

4 Dada ( ) = trace um esboo do grfico de . Mostre que no existe nmero

intervalo aberto (2,2) tal que

no

( )=

(2) (2)

2 (2)

Que condio da hiptese do teorema do valor mdio no verificada para

2
=2?
Soluo:
Um esboo do grfico de

mostrado na figura 16.7.

y

-2

-1

Figura 16.7 Grfico da Funo ( ) =

( )=

2
3

Portanto,
( )=

2
3

quando

62

(2) (2) 4
=
2 (2)
No existe nmero para o qual 23

4
4

= 0.

= 0.

A funo continua no intervalo fechado [2,2]. Contudo, no derivvel no

intervalo aberto (2,2), pois (0) no existe. Portanto, a condio (ii) da hiptese do
teorema de valor mdio no verificada para quando = 2
= 2.

17. Assntotas.
17.1 Assntotas Horizontais.
=

A reta
( ) lim

uma assntota horizontal de do grfico de uma funo

( )= .

Ou
( )= .

lim

Exemplos.
1 As reta
=

+2

=1e

= 1 so assntotas horizontais do grfico de

Porque,
lim

+2

=1

lim

+2

= 1.

Y
1

X
-1

Figura 17.1 Grfico da Funo

= ( ) se ocorrer:

63

2 A reta
=

= 1 uma assntota horizontal da funo

1
, pois
1+

lim

1
= 1.
1+

Figura 17.2 Grfico da funo

17.2 Assntotas Verticais.

A reta = uma assntota vertical do grfico de uma funo
pelo menos uma das situaes:
( ) lim

( ) = +
( ) =

( ) lim

( ) lim
(

) lim

( ) = +
( ) =

Exemplos.
1 - A reta
lim

= 0 uma assntota vertical da funo

= ln ( ), pois

( ) = .

Figura 17.3

= ( ) se ocorrer

64

2 Reta
lim

= 1 uma assntota vertical de funo

, pois

1
= +
( 1)

Figura 17.4 Grfico da

=(

17.3 Assntotas Oblquas.

A reta

+ uma assntota oblqua do grfico de uma funo

( ) lim [ ( ) (

+ )] = 0 ou

( ) lim [ ( ) (

+ )] = 0

= ( ), se ocorrer:

possvel se mostrar que

= lim

( )

E uma vez determinado o k, que

= lim [ ( )

].

(1) Substituindo-se , obtem-se, analogamente, as expresses de k e de b para

outra possvel assntota oblqua.
(2) Em ambos os caso, se no existir um dos limites acima de inidas para k e b,
no existe a assntota oblqua.
(3) As assntotas horizontais so casos particulares das assntotas oblquas, ocorrendo
quando = 0.
(4) Uma funo pode ter no mximo duas assntotas oblquas, incluindo as horizontais.

65

18. Esboo Grfico de Funes.

Para obtermos o esboo grfico de uma funo, devemos seguir os seguintes passos:
1.
2.
3.
4.
5.
6.
7.
8.

Determinar o domnio de .
Calcular os pontos de interseco do grfico com os eixos coordenados;
Determinar os pontos;
Determinar os pontos de Mximos e Mnimos;
Estudar a concavidade;
Determinar os pontos de inflexo;
Determinar as assntotas;
Esboar o grfico.

Exemplos.
1 - Esboar o grfico da funo ( ) = (

1) .

Soluo:
( ) = ;
1) Domnio:
2) Interseces com os eixos coordenados: se = 0, ento = 1 e, se
= 0 ento
(
)
(
)
(
)
1; a curva passa pelos pontos 1, 0 , 1, 0 e 0, 1 .
3) Pontos crticos de : ( ) = 6 ( 1 ) . Logo, resolvendo a equao ( ) = 0,
obtemos = 0, = 1 e = 1, que so os pontos crtico de .
4) Mximos e mnimos relativos de : ( ) = 6( 1)(5 1). Logo, (0) > 0 e 0
o ponto mnimo relativo de . (1) = 0 e o teste da segunda derivada no nos diz
nada. Usando, ento, o teste da primeira derivada para analisar a mudana de sinal
temos: ( ) < 0, para > 0, ento = 1 no ponto extremo de .
5) Concavidade

( ) = 6(

1)(5

( ) > 0 se

(, 1)

( ) < 0 se

1,

1) = 0 implica que

(1, +).

Concluso: : tem C.V.C. nos intervalos (, 1),

tem C.V.B. nos intervalos 1,

= 1 e

e (1,+).

,1 .

6) Ponto de inflexo: As abscissas dos pontos de inflexo de

7) Assntotas de : A curva no possui assntotas;
8) Esboo do grfico de .

so

= 1 e

66

Figura 18.1 Grfico da Funo ( ) = (

2 Esboar o gr ico da funo ( ) = 7 + 12 3

1) .

Soluo:
( ) = ;
1) Domnio:
2) Interseco com os eixos coordenados:
= 0, ento = 7
= 0, = 1
7
=
2;
( )
3)

:
= 12 6 6 .
,

( )

= 0,

= 2, = 1
.
( )
( )
4)

:
= 6 12 .
,
1 <0
1

.
:

5)
(

) < 0 se

2) > 0

2 ponto de mnimo.

) = 6 12 = 0

= .

)>0

<

> .

Concluso: o gr ico de

tem C. V. C. em ,

e tem C. V. B. Em , + .

6) Ponto de in lexo: A abscissa do ponto de in lexo de

7) Assntotas de : A curva no possui assntotas.

8) Esboo do grfico de .

Figura 18.2 Grfico da Funof(x) = 7 + 12x + 3x 2x .

67

19. Problemas de Otimizao Envolvendo mximos e Mnimos.

Exemplos.
1 - No planejamento de uma lanchonete foi estimado que se existem lugares para 40 a 80
pessoas o lucro semanal ser de R$ 70,00 por lugar,contudo a capacidade de assentos esta
acima de 80 lugares,o lucro semanal em cada lugar ser reduzido em 50 centavos pelo numero
de lugares excedentes.qual devera ser a capacidade de assentos para se obter o maior lucro
semanal?

Soluo:
Sejam x= o numero de lugares que a lanchonete comporta;
P= o numero de cruzeiros no lucro total semanal,
O valor de p depende de x e obtido ao multiplicarmos x pelo numero de cruzeiros
obtido no lucro por lugar. Quando 40
80, o lucro por lugar $ 70,00 e por tanto
= 70 .contudo,quando > 80 o lucro de cruzeiros por lugar [ 70 0,5( 80 )],ou
seja,

[70 0,5( 80 )] = 100 0,5

( )=

70
110 0,5

. Assim, temos

40
80

80
220

O extremo superior de 220 para obtido notando que 110 0,5

220 e 110 0,5 negativo para > 220.

=0 quando

Embora x seja um inteiro, por definio, para termos uma funo continua devemos
tomar x para todos os valores reais no intervalo [40, 220]. Notemos que p continua em 80,
pois
lim

( ) = lim 70 = 5.600.

e
lim

( ) = lim (110 0,5 ) = 5.600.

De onde resulta que

lim ( ) = 5.600 = (80).

68

Logo, continua no intervalo fechado [ 40, 220] e o teorema do valor extremo

garante a existncia de um valor Mximo absoluto de neste intervalo.
Quando 40 < x < 80, p(x) = 70 e (80) = 30. Determinando ( ) = 0,
Temos,
110

= 0

= 110.
Logo, os nmeros crticos de p so 80 e 110. Calculamos ( ) nos extremos do
intervalo [40, 220] e nos nmeros crticos, temos
(40) = 320, (80) = 5.600, (110) = 6050
(220) = 0. Ento, o valor Maximo
absoluto de p 6050 e o corre quando x = 110. A capacidade de assentos deve ser de 110
lugares, que da um lucro semanal total de $ 6050,00.
2 Um fabricante deseja construir caixas de papelo sem tampa e de base regular, dispondo
de um pedao retangular de papelo com 8 cm de lado e 15cm de comprimento.Para tanto,
deve-se tirar de cada canto quadrados iguais,em seguida viram-se os lados para
cima.determine o comprimento dos lados dos quadrados que devem ser cortados para a
produo de uma caixa de volume Maximo.
Soluo:

A altura da caixa x; a largura (8 2x) e o comprimento (15 2x), observando que 0 <
x < 4.
Logo, devemos maximizar:
V(x) = x (8 2x)(15 2x) = 4

- 46

+ 120x.

Derivando-se e igualando a zero:

V( ) = 12

Obtemos

= 6 ou

- 92 + 120 = ( 6)(12 20) = 0,

= . Mas, 6 < (0,4); ento,

logo, estudando o sinal de V,

o ponto Maximo. Ento

o nico ponto critico de v.

1,6

v= 90,74

69

19.3 Um tanque sem tampa em forma de cone feito com material plstico, tem capacidade
de 1.000 . Determine as dimenses do tanque que minimiza a quantidade do plstico usada
na sua fabricao.
Soluo:
A rea do cone
+ , em que a ltima igualdade usamos o teorema de Pitgoras.
Por outro lado, o volume do tanque de 1.000
logo,
1.000=
E =

r h.

. Substituindo na expresso da rea. Temos:

=
Como antes minimizaremos

=(

3.000

) . Logo:
( )=

Em que = (3.000) . Derivando-se e igualando a zero, obtemos que

8,733
aproximadamente, 12,407 .
Conseqentemente,

aproximadamente, 418,8077

aproximadamente,