Teorema do Valor Médio e suas Conseqüências

Revisão para a terceira prova
Aula 30
Alexandre Nolasco de Carvalho

Universidade de São Paulo
São Carlos SP, Brazil
22 de Maio de 2014
Primeiro Semestre de 2014
Turma 2014106 - Engenharia Mecânica
Alexandre Nolasco de Carvalho ICMC - USP SMA 301 Cálculo I

O Teorema do Valor Médio e suas Conseqüências
O Teorema do Valor Médio é um dos Teoremas mais importantes

do Cálculo. A sua demonstração é feita mostrando primeiramente
o caso particular f (a) = f (b) conhecido como Teorema de Role.
Teorema (do Valor Médio - TVM)
Seja f : [a, b] → R uma função contı́nua em [a, b] e diferenciável
em (a, b). Então existe c ∈ (a, b) tal que
f (b) − f (a) = f ′ (c)(b − a) ,
ou seja
f (b) − f (a)
f ′ (c) = .
b−a

Teorema (De Cauchy)
Se f e g são contı́nuas em [a, b] e diferenciáveis em (a, b), existe
c ∈ (a, b) tal que
[f (b) − f (a)]g ′ (c) = [g (b) − g (a)]f ′ (c).
Prova: Considere h(x) = [f (b) − f (a)]g (x) − [g (b) − g (a)]f (x) e

aplique o Teorema de Role.

Regras de L’Hospital
As regras de L’Hospital se aplicam a cálculos de limites que

apresentam as seguintes indeterminações
0 ∞
ou .
0 ∞

Teorema (Regra de L’Hospital)
Sejam f e g funções differenciáveis em x com g ′ (x) 6= 0 em
(p − r , p + r )\{p} para algum r > 0. Se
lim f (x) = 0 = lim g (x)

x→p x→p
f ′ (x) f (x)
e lim = ℓ ∈ R (ou ℓ = ±∞), então lim =ℓ
x→p g ′ (x) x→p g (x)

Prova: Como os valores de f (p) e g (p) não influem no cálculo do
limite, podemos assumir que f (p) = g (p) = 0. Assim, do Teorema
de Cauchy, para cada x ∈ (p − r , p + r )\{p} existe c entre x e p
(distinto de ambos) tal que
f (x) − f (p) f ′ (c) f ′ (x)

= lim = lim ′ = lim ′ .
x→p g (x) − g (p) x→p g (c) x→p g (x)

Observação: A regra de L’Hospital ainda será válida se, em lugar
de x → p , tivermos x → p + , x → p − , x → +∞ ou x → −∞ .

a Regra de L’Hospital: Sejam f e g funções deriváveis em
2¯
(p − r , p + r )\{p} , r > 0 , com g ′ (x) 6= 0 para 0 < |x − p| < r .
Se
lim f (x) = +∞ = lim g (x)
x→p x→p
f ′ (x)
e o limite lim existir (ou divergir para ± infinito), então o
x→p g ′ (x)
f (x)
limite lim também existirá (ou divergirá para ± infinito) e
x→p g (x)
teremos
f (x) f ′ (x)
lim = lim ′ .
x→p g (x) x→p g (x)

Observação: A 2¯a regra de L’Hospital ainda será válida se, em
lugar de x → p , tivermos x → p + , x → p − , x → +∞ ou
x → −∞ . Esta regra também permanecerá válida caso tenhamos
−∞ em lugar de +∞ em um ou ambos os limites.
Observação: As Regras de L’Hospital se aplicam a

0 ∞
indeterminações da forma e . As outras formas de
0 ∞
indeterminação, 0 · ∞, ∞ − ∞, 0 , ∞0 , 1∞ , podem ser reduzidas a
0
estas.

Monotonicidade
Agora vamos obter informação do comportamento de uma função

a partir de suas derivadas (usando o Teorema do Valor Médio).
Corolário (Teste de Monotonicidade)
Seja f uma função contı́nua no intervalo [a, b] e diferenciável no
intervalo (a, b).
◮ Se f ′ (x) > 0 para todo x ∈ (a, b), então f será estritamente
crescente em [a, b].
◮ Se f ′ (x) < 0 para todo x ∈ (a, b) então f será estritamente
decrescente em [a, b].

É fácil ver que, se f for diferenciável e crescente (resp.
decrescente) em (a, b), então f ′ (x) ≥ 0 (resp. f ′ (x) ≤ 0), para
todo x ∈ (a, b). A recı́proca também é verdadeira.
Corolário
Seja f uma função contı́nua no intervalo [a, b] e diferenciável no
intervalo (a, b).
◮ Se f ′ (x) ≥ 0 para todo x ∈ (a, b), então f será crescente em
[a, b].
◮ Se f ′ (x) ≤ 0 para todo x ∈ (a, b) então f será decrescente em
[a, b].

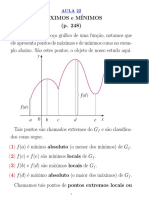
Máximos e Mı́nimos
Definição
Um ponto crı́tico de uma função f é um ponto c onde ou
f ′ (c) = 0 ou f ′ (c) não existe.
Proposição
Seja I um intervalo aberto e f : I → R uma função diferenciável.
Se c ∈ I for um ponto extremo (máximo ou mı́nimo) de f , então
f ′ (c) = 0.
Observação: Todo ponto extremo de uma função diferenciável em

num intervalo aberto é um ponto crı́tico e que nem todo ponto
crı́tico é um ponto extremo. Logo, se f estiver definida em um
intervalo aberto, procuramos os pontos extremos entre os pontos
crı́ticos.

Observações:
◮ Se I não for um intervalo aberto podemos ter pontos crı́ticos
para os quais a derivada não é zero.
◮ Um ponto crı́tico não precisa ser um ponto extremo.
◮ x = 0 é um ponto de mı́nimo para f (x) = |x| (f ′ (0) 6 ∃).

O Teorema de Weierstrass afirma que uma função contı́nua em um
intervalo fechado tem um valor máximo e um mı́nimo global, mas
não diz como encontrar esses valores extremos.
Notemos que o valor extremo de uma função contı́nua definida

num intervalo fechado ou ocorre num ponto crı́tico ou ocorre em
um extremo do intervalo.

Para encontrar os valores máximos e mı́nimos globais de uma
função contı́nua f num intervalo fechado [a, b] :
1. Encontre os valores de f nos pontos crı́ticos de f em (a, b).

2. Encontre os valores de f nos extremos do intervalo.
3. O maior valor das etapas 1 e 2 é o valor máximo global e o
menor desses valores é o mı́nimo global.

A proposição seguinte segue dos corolários do TVM.
Proposição (Critério da derivada primeira)
Seja f uma função contı́nua e c um ponto crı́tico de f .
(i) Se o sinal de f ′ mudar de positivo para negativo em c, então
f tem um máximo local em c.
(ii) Se o sinal de f ′ mudar de negativo para positivo em c, então
f tem um mı́nimo local em c.

Teorema
Sejam f : [a, b] → R derivável em (a, b) e p ∈ [a, b]. Valem as
afirmações:
(i) Se f ′ (p) = 0 e f ′ for crescente em (a, b), então p será ponto
de mı́nimo local de f .
(ii) Se f ′ (p) = 0 f ′ for decrescente em (a, b), então p será ponto
de máximo local de f .

Proposição (Critério da derivada segunda)
Suponhamos que f : [a, b] → R admita derivadas até segunda
ordem contı́nuas em (a, b) e seja p ∈ (a, b). Valem as afirmações:
(i) Se f ′ (p) = 0 e f ′′ (p) > 0, então p será ponto de mı́nimo
local de f .
(ii) Se f ′ (p) = 0 e f ′′ (p) < 0, então p será ponto de máximo
local de f .

Concavidade
Sejam f : (a, b) → R uma funçãõ diferenciável e p ∈ (a, b). A reta
tangente ao gráfico de f no ponto (p, f (p)) é o gráfico de
Tp (x) = f (p) + f ′ (p)(x − p).
Definição
Seja f derivável em (a, b) . Diremos que
◮ f tem concavidade para cima em (a, b) se, para quaisquer
x, p ∈ (a, b), com x =
6 p, tivermos
f (x) > Tp (x).
◮ f tem concavidade para baixo em (a, b) se, para quaisquer

x, p ∈ (a, b), com x =
6 p, tivermos
f (x) < Tp (x).

O próximo teorema estabelece condições suficientes para que uma
função f tenha concavidade para cima ou para baixo.
Teorema (Critério para determinar concavidade-I)
Seja f uma função derivável em (a, b). Valem as afirmações
(i) Se f ′ for estritamente crescente em (a, b), então f tem
concavidade para cima em (a, b).
(ii) Se f ′ for estritamente decrescente em (a, b), então f tem
concavidade para baixo em (a, b).

Corolário (Critério para determinar concavidade-II)
Seja f uma função derivável até segunda ordem em (a, b) . Valem
as afirmações
(i) Se f ′′ (x) > 0, para todo x ∈ (a, b), então f tem concavidade
para cima (a, b).
(ii) Se f ′′ (x) < 0, para todo x ∈ (a, b), então f tem concavidade
para baixo em (a, b) .

Pontos de Inflexão
Definição
Seja f uma função contı́nua em p ∈ Df . Diremos que p é ponto
de inflexão de f se a concavidade de f muda em p.
Definição
Se f for uma função diferenciável em p ∈ (a, b) e p for um ponto
de inflexão de f , diremos que p é um ponto de inflexão
horizontal, se f ′ (p) = 0 (ponto crı́tico). Caso contrário diremos
que p é um ponto de inflexão oblı́quo.

Corolário
Se f for duas vezes diferenciável em (a, b) e p ∈ (a, b) for um
ponto de inflexão de f , então f ′′ (p) = 0.
Teorema
Seja f três vezes diferenciável em (a, b) com derivada terceira
contı́nua. Se p ∈ (a, b) for tal que f ′′ (p) = 0 e f ′′′ (p) 6= 0, então p
será um ponto de inflexão de f .

Polinônios de Taylor
O polinômio
f ′′ (p) f (n) (p)

Pn (x) = f (p)+f ′ (p)(x −p)+ (x −p)2 + ... + (x −p)n ,
2 n!
é chamado de polinômio de Taylor de ordem n de f (x) ao

redor de p.

O teorema a seguir nos fornece uma fórmula para o erro.
Teorema (Fórmula de Taylor com resto de Lagrange)
Suponhamos que a função f (x) seja (n + 1) vezes diferenciável no
ao redor do ponto p. Então
f n+1 (x̄)
Rn (x) = (x − p)n+1
(n + 1)!
para algum x̄ entre x e p.

Assı́ntotas Verticais, Horizontais e Oblı́quas
Definição (Assı́ntota Vertical)

A reta x = p é uma assı́ntota vertical ao gráfico de f se
lim f (x) = +∞ ou lim f(x) = +∞ ou lim f(x) = +∞

x→p x→p− x→p+
ou
lim f (x) = −∞ ou lim f(x) = −∞ ou lim f(x) = −∞.

x→p x→p− x→p+

Definição (Assı́ntota Horizontal)
A reta y = L é uma assı́ntota horizontal ao gráfico de f se
lim f (x) = L ou lim f (x) = L

x→+∞ x→−∞
Exemplo
x2 − 1
A reta y = 1 é assı́ntota horizontal de f (x) = .
x2 + 1

Definição (Assı́ntota Oblı́qua)
Seja f uma função. Se existir uma reta de equação y = mx + n
tal que
lim [f (x) − (mx + n)] = 0
x→+∞
ou
lim [f (x) − (mx + n)] = 0 ,
x→−∞
então tal reta será dita uma assı́ntota para f . Se m = 0, teremos

uma assı́ntota horizontal e, se m 6= 0, teremos uma assı́ntota
oblı́qua.

Procedimento para determinar assı́ntotas: Primeiro determine
m, caso exista, através do limite
f (x)
m = lim .
x→±∞ x
Em seguida, calcule
n = lim [f (x) − mx].

x→±∞
Se n for finito então y = mx + n será assı́ntota para x → ±∞.

Esboço de Gráficos de Funções
A lista de informações necessárias para fazer um esboço do gráfico

de uma função.
1. Explicite o domı́nio da função.
2. Calcule os limites laterais de f nos pontos onde f não é
contı́nua ou não estiver definida.
3. Calcule os limites de f para x → +∞ e x → −∞.
4. Determine as assı́ntotas.
5. Localize as raı́zes de f .
6. Encontre os pontos crı́ticos e determine os intervalos de
crescimento e de decrescimento.
7. Determine os pontos de máximo e mı́nimo e calcule os valores
da função nestes pontos.
8. Estude a concavidade e destaque os pontos de inflexão.
9. Esboce a curva utilizando todas as informações anteriores.

Anti-derivadas ou Primitivas
Sabemos que a derivada de uma função constante é zero.

Entretanto, uma função pode ter derivada zero em todos os pontos
x
de seu domı́nio e não ser constante; por exemplo f (x) = é tal
|x|
que f ′ (x) = 0 em todo ponto de seu domı́nio, mas não é constante.
No entanto vale o seguinte resultado
Corolário
Se f for contı́nua em [a, b] e diferenciável em (a, b) e f ′ (x) = 0
para todo x ∈ (a, b), então f será constante.

Corolário
Duas funções f , g : (a, b) → R tais que f ′ (x) = g ′ (x) para todo
x ∈ (a, b) diferem por uma constante.
Definição
Uma primitiva ou anti-derivada de f definida em um intervalo I é
uma função derivável F definida em I tal que
F ′ (x) = f (x), para todo x ∈ I .
Observação: Se F for uma primitiva de f , então F será contı́nua,

pois F é derivável. Duas primitivas de uma função definida em um
intervalo diferem por uma constante.

Segue que as primitivas de f são da forma F (x) + k, com k
constante. Denotamos por
Z
f (x) dx = F (x) + k, k constante
à famı́lia de primitivas ou integral indefinida de f .

Das fórmulas de derivação já vistas seguem as seguintes primitivas
Z Z
(a) c dx = cx + k; (b) e x dx = e x + k;
x α+1
Z Z
(c) x α dx = , α 6= −1; (d) cos x dx = sen x + k;
α+1
1 1
Z Z
(e) dx = ln x + k, x > 0; (f ) dx = ln(−x) + k, x < 0;
Z x Z x
(g ) sen x dx = − cos x + k; (h) sec2 x dx = tg x + k;
1
Z Z
(i ) sec x tg x dx = sec x + k; (j) dx = arctg x + k;
Z Z 1 + x2
(k) sec xdx = ln |sec x +tg x|+ k; (l ) tg x dx = − ln | cos x| + k;
1
Z
(m) √ dx = arcsen x +k.
1−x 2

Mudança de Variável ou Regra da Substituição
Sejam f e g tais que Im(g ) ⊂ Df . Suponhamos que F seja uma

primitiva de f .
Então F (g (x)) é uma primitiva de f (g (x))g ′ (x), de fato, pela

Regra da Cadeia,
[F (g (x))]′ = F ′ (g (x))g ′ (x) = f (g (x))g ′ (x).
Portanto, Z
f (g (x))g ′ (x) dx = F (g (x)) + k ,
onde k é uma constante arbitrária.

Integração por Partes
Sejam f , g : [a, b] → R diferenciáveis em (a, b). Então, para cada

x ∈ (a, b), vale
[f (x)g (x)]′ = f ′ (x)g (x) + f (x)g ′ (x),
ou seja,
f (x)g ′ (x) = [f (x)g (x)]′ − f ′ (x)g (x) .
Logo
Z Z
′
f (x)g (x) dx = f (x)g (x) − f ′ (x)g (x) dx . (1)

A integral de Darboux
Vamos dar uma noção (devido a Darboux) equivalente à noção de

integral de Riemann que apresenta algumas vantagens na obtenção
de critérios de integrabilidade. Seja f : [a, b] → R uma função
limitada e
P : a = x0 < x1 < x2 < · · · < xnP = b,
uma partição de [a, b]. Sejam
Mi = sup f (x) e mi = inf f (x), 1 6 i 6 n.
x∈[xi −1 ,xi ] x∈[xi −1 ,xi ]
Defina a soma superior Sp (inferior sP ) de f relativamente à

partição P por
nP nP
!
X X
SP = Mi ∆xi sP = mi ∆xi .
i =1 i =1

Seja P uma partição e Q uma partição obitida de P adicionando
um ponto x̄. É imediato que SQ ≤ SP e que sQ ≥ sP . Mais
geralmente, se P ⊂ Q temos que SQ ≤ SP e que sQ ≥ sP .
Dadas duas partições P e Q denotamos por P ∪ Q à partição

formada pelos pontos de P e de Q.
Segue que, dadas duas partições P e Q quaisquer
inf f (x)(b − a) ≤ sP ≤ sP∪Q ≤ SP∪Q ≤ SQ ≤ sup f (x)(b − a)

x∈[a,b] x∈[a,b]

Definição
Se P denota o conjunto de todas as partições do intervalo [a, b] e
f : [a, b] → R é uma função limitada a integral superior (inferior)
de f é definida por
Z b Z b !
f (x)dx = inf {SP : P ∈ P} f (x)dx = sup {sP : P ∈ P}
a a
Definição
Uma função limitada f : [a, b] → R é Darboux integrável se, e
somente se,
Z b Z b
f (x)dx = f (x)dx
a a
Z b
e neste caso o valor comum é denotado por D f (x)dx
a

Critério de Integrabilidade para integrais de Darboux
Teorema
Uma função limitada f : [a, b] → R é Darboux integrável se, e
somente se, dado ǫ > 0 existe partição P ∈ P tal que
SP − sP < ǫ.
Recorde que, se R, Q ∈ P então,

Z b Z b
SR ≥ SR∪Q ≥ f (x)dx ≥ f (x)dx ≥ sR∪Q ≥ sQ .
a a

Teorema
Uma função limitada f : [a, b] → R é Riemann integrável se, e
somente se, é Darboux integrável e em qualquer caso
Z b Z b
D f (x)dx = f (x)dx.
a a

Critério de Integrabilidade
Proposição
Se f for contı́nua em [a, b] então,
◮ f é uniformemente contı́nua; isto é, dado ǫ > 0 existe δ > 0
(que depende somente de ǫ) tal que, se x, y ∈ [a, b] e
|x − y | < δ então, |f (x) − f (y )| < ǫ.
◮ f é Darboux integrável em [a, b].

Definição Z b
Se existir a integral f (x) dx , então definiremos
a
Z a Z b
f (x) dx = − f (x) dx .
b a

Propriedades da Integral
Sejam f , g : [a, b] → R funções integráveis. Então
◮ Para todo k ∈ R, a função f + kg é integrável e
Z b Z b Z b
(f + kg )(x) dx = f (x) dx + k g (x) dx.
a a a
◮ Se a ≤ c < d ≤ b, então f é integrável em [c, d].
Rb
◮ Se f (x) ≥ 0, para todo x ∈ [a, b], então a f (x) dx ≥ 0. Em
particular, se g (x) ≤ f (x) para todo x ∈ [a, b], então
Z b Z b
g (x) dx ≤ f (x) dx.
a a
Rc Rb
◮ Se existirem as integrais a f (x) dx e c f (x) dx , com
Rb
c ∈ [a, b], então existirá a integral a f (x) dx e
Z b Z c Z b
f (x) dx = f (x) dx + f (x) dx .
a a c

O Teorema Fundamental do Cálculo
Teorema (Teorema Fundamental do Cálculo)

Se f : [a, b] → R é contı́nua então, a função g definida por
Z x
g (x) = f (t) dt, a≤x ≤b
a
é diferenciável em [a, b] e g ′ (x) = f (x).

Cálculo de Integrais Definidas
Do Teorema Fundamental do Cálculo, se f : [a, b] → R é contı́nua

então Z x
F (x) = f (t)dt
a
é uma primitiva de f . Se G é outra primitiva de f , temos que
existe uma constante k ∈ R tal que F (x) = G (x) + k. Como
F (a) = 0 temos que G (a) = −k e
Z x
F (x) = f (t)dt = G (x) − G (a).
a
Em particular
Z b
f (t)dt = G (b) − G (a).
a

Cálculo de áreas
Então A é o conjunto dos pontos (x, y ) ∈ R2 limitado pelas retas

x = a, x = b e pelos gráficos das funções f e g , onde f (x) ≥ g (x),
para todo x ∈ [a, b]. Segue que
Z b Z b Z b
área A = [f (x) − g (x)] dx = f (x)dx − g (x)dx
a a a

Deslocamento e Espaço Percorrido
Consideremos uma partı́cula que se desloca sobre o eixo x com

equação de posição x = x(t) e com velocidade v = v (t) contı́nua
dx
em [a, b]. Sabemos que (t) = v (t), ou seja, x(t) é uma
dt
primitiva de v (t). Portanto, pelo Teorema Fundamental do
Cálculo, temos Z b
v (t) dt = x(b) − x(a) (2)
a
que é o deslocamento da partı́cula entre os instantes a e b.

Para calcular a distância percorrida durante o intervalo de tempo,
teremos que considerar os intervalos quando v (t) ≥ 0 e também
quando v (t) ≤ 0. Portanto, definimos por
Z b
| v (t)| dt (3)
a
o espaço percorrido pela partı́cula entre os instantes a e b .

Observação: Se v (t) ≥ 0, para todo t ∈ [a, b], então (2) e (3)
implicam que o espaço percorrido pela partı́cula e o seu
deslocamento coincidem entre os instantes a e b e são iguais à
Z b
v (t) dt
a
que determina a área do conjunto limitado pelas retas t = a, t = b,

pelo eixo 0t e pelo gráfico de v = v (t). Veja a figura abaixo.

v (t) ✻
v = v (t)
✲
a b t

Observação: Seja c ∈ [a, b] e suponha que v (t) ≥ 0 em [0, c] e
v (t) ≤ 0 em [c, b] conforme a figura.
v (t) ✻
v = v (t)
✲ A1
✲
a b t
A2 ✙

Então o deslocamento da partı́cula é dado por (2) acima, ou seja,
Z b
x(b) − x(a) = v (t) dt = A1 − A2 ,
a
mas a distância percorrida entre os instantes a e b é dada por

(3), ou seja,
Z b Z c Z b
| v (t)| dt = v (t) dt − v (t) dt = A1 + A2 .
a a c
Logo, neste caso, a distância percorrida percorrida não coincidem.

Trabalho
Nesta seção, vamos definir trabalho realizado por uma força que
varia com a posição. No caso de uma força constante F , o
trabalho realizado é definido pelo produto da força pela distância d
que o objeto se move:
τ = Fd , trabalho = força × distância.
Vamos considerar agora uma força F que atua sobre uma partı́cula
que se desloca sobre o eixo x. Suponhamos que esta força seja
paralela ao deslocamento e variável com a função de posição x.
Então escrevemos
~ (x) = f (x)~i ,
F
onde f (x) é a componente de F ~ (x) na direção do deslocamento
(isto é, na direção de ~i ).

Com isto
Definição
O trabalho τ realizado por uma força F ~ (x) = f (x)~i sobre uma
partı́cula no deslocamento de x = a até x = b é dado por
n
X Z b
τ = lim f (ci )∆xi = f (x) dx .
∆P →0 a
i =1

Teorema do Valor Médio e suas Conseqüências

Enviado por

Dados do documento

Título original

Direitos autorais

Formatos disponíveis

Compartilhar este documento

Compartilhar ou incorporar documento

Opções de compartilhamento

Você considera este documento útil?

Este conteúdo é inapropriado?

Direitos autorais:

Formatos disponíveis

Teorema do Valor Médio e suas Conseqüências

Enviado por

Direitos autorais:

Formatos disponíveis

Revisão para a terceira prova

Alexandre Nolasco de Carvalho

Alexandre Nolasco de Carvalho ICMC - USP SMA 301 Cálculo I

O Teorema do Valor Médio é um dos Teoremas mais importantes

f (b) − f (a) = f ′ (c)(b − a) ,

Alexandre Nolasco de Carvalho ICMC - USP SMA 301 Cálculo I

[f (b) − f (a)]g ′ (c) = [g (b) − g (a)]f ′ (c).

Prova: Considere h(x) = [f (b) − f (a)]g (x) − [g (b) − g (a)]f (x) e

Alexandre Nolasco de Carvalho ICMC - USP SMA 301 Cálculo I

As regras de L’Hospital se aplicam a cálculos de limites que

Alexandre Nolasco de Carvalho ICMC - USP SMA 301 Cálculo I

lim f (x) = 0 = lim g (x)

Alexandre Nolasco de Carvalho ICMC - USP SMA 301 Cálculo I

f (x) − f (p) f ′ (c) f ′ (x)

Alexandre Nolasco de Carvalho ICMC - USP SMA 301 Cálculo I

Alexandre Nolasco de Carvalho ICMC - USP SMA 301 Cálculo I

Alexandre Nolasco de Carvalho ICMC - USP SMA 301 Cálculo I

Observação: As Regras de L’Hospital se aplicam a

Alexandre Nolasco de Carvalho ICMC - USP SMA 301 Cálculo I

Agora vamos obter informação do comportamento de uma função

Alexandre Nolasco de Carvalho ICMC - USP SMA 301 Cálculo I

Alexandre Nolasco de Carvalho ICMC - USP SMA 301 Cálculo I

Observação: Todo ponto extremo de uma função diferenciável em

Alexandre Nolasco de Carvalho ICMC - USP SMA 301 Cálculo I

Alexandre Nolasco de Carvalho ICMC - USP SMA 301 Cálculo I

Notemos que o valor extremo de uma função contı́nua definida

Alexandre Nolasco de Carvalho ICMC - USP SMA 301 Cálculo I

1. Encontre os valores de f nos pontos crı́ticos de f em (a, b).

Alexandre Nolasco de Carvalho ICMC - USP SMA 301 Cálculo I

Alexandre Nolasco de Carvalho ICMC - USP SMA 301 Cálculo I

Alexandre Nolasco de Carvalho ICMC - USP SMA 301 Cálculo I

Alexandre Nolasco de Carvalho ICMC - USP SMA 301 Cálculo I

Tp (x) = f (p) + f ′ (p)(x − p).

f (x) > Tp (x).

◮ f tem concavidade para baixo em (a, b) se, para quaisquer

f (x) < Tp (x).

Alexandre Nolasco de Carvalho ICMC - USP SMA 301 Cálculo I

Alexandre Nolasco de Carvalho ICMC - USP SMA 301 Cálculo I

Alexandre Nolasco de Carvalho ICMC - USP SMA 301 Cálculo I

Alexandre Nolasco de Carvalho ICMC - USP SMA 301 Cálculo I

Alexandre Nolasco de Carvalho ICMC - USP SMA 301 Cálculo I

f ′′ (p) f (n) (p)

é chamado de polinômio de Taylor de ordem n de f (x) ao

Alexandre Nolasco de Carvalho ICMC - USP SMA 301 Cálculo I

para algum x̄ entre x e p.

Alexandre Nolasco de Carvalho ICMC - USP SMA 301 Cálculo I

Definição (Assı́ntota Vertical)

lim f (x) = +∞ ou lim f(x) = +∞ ou lim f(x) = +∞

lim f (x) = −∞ ou lim f(x) = −∞ ou lim f(x) = −∞.

Alexandre Nolasco de Carvalho ICMC - USP SMA 301 Cálculo I

lim f (x) = L ou lim f (x) = L

Alexandre Nolasco de Carvalho ICMC - USP SMA 301 Cálculo I

então tal reta será dita uma assı́ntota para f . Se m = 0, teremos

Alexandre Nolasco de Carvalho ICMC - USP SMA 301 Cálculo I

n = lim [f (x) − mx].

Se n for finito então y = mx + n será assı́ntota para x → ±∞.

Alexandre Nolasco de Carvalho ICMC - USP SMA 301 Cálculo I

A lista de informações necessárias para fazer um esboço do gráfico

Alexandre Nolasco de Carvalho ICMC - USP SMA 301 Cálculo I

Sabemos que a derivada de uma função constante é zero.

No entanto vale o seguinte resultado

Alexandre Nolasco de Carvalho ICMC - USP SMA 301 Cálculo I

F ′ (x) = f (x), para todo x ∈ I .