Manual de Apoio - Limites de Funções e Continuidade de Funções

2023/2024
TEMA:Limites Funções e Continuidade de Funções

1
de
1. LIMITE DE UMA FUNÇÃO

1.1 Definição
Diz-se que o limite da função f(x) quando x tende a “a” é igual

ao número real L se, e somente se, os números reais f(x) para os
infinitos valores de x permanecem próximos a L, sempre que x
estiver muito próximo de “a”. Indica-se lim 𝑓(𝑥) = 𝐿.
𝑥→𝑎
Se para todo e qualquer número 𝜀 > 0, existir 𝛿 > 0 tal que se

0 < |𝑥 − 𝑎| < 𝛿 então |𝑓(𝑥) − 𝐿| < 𝜀.
Simbolicamente, temos:
𝐥𝐢𝐦 𝒇(𝒙) = 𝑳 ⇔ ∀𝜺 > 𝟎, ∃𝜹 > 𝟎 / se 𝟎 < |𝒙 − 𝒂| < 𝜹 ⇒ |𝒇(𝒙) − 𝑳| < 𝜺.
𝒙→𝒂
Definição de Limite (Segundo Heine)
Seja 𝑓(𝑥) uma função de variável real e, 𝒂 e 𝒃 constantes

quaisquer finitas ou infinitas, diz-se que 𝑓(𝑥) tende para 𝒃
quando 𝑥 tende para 𝒂, se a toda a sucessão de valores de 𝑥
tendente para 𝒂, corresponde uma sucessão de valores de 𝒇(𝒙)
tendente para 𝒃, e escreve-se: lim 𝑓(𝑥) = 𝑏.
𝑥→𝑎
Definição de Limite (Segundo Cauchy)
Sendo 𝒂 e 𝐿 números reais, diz-se que uma função 𝑓(𝑥) tende

para 𝒂, se dado um número positivo 𝛿(𝑑𝑒𝑙𝑡𝑎), se pode sempre
associar-se-lhe um número 𝜀 (é𝑝𝑠𝑖𝑙𝑜𝑛), de modo que |𝑓(𝑥) − 𝐿| < 𝜀,
desde que |𝑥 − 𝑎| < 𝛿 com 𝑥 ≠ 𝑎.
Simbolicamente, temos:
𝐥𝐢𝐦 𝒇(𝒙) = 𝑳 ⇔ ∀𝜺 > 𝟎, ∃𝜹 > 𝟎 / se 𝟎 < |𝒙 − 𝒂| < 𝜹 ⇒ |𝒇(𝒙) − 𝑳| < 𝜺.

𝒙→𝒂
Dionísio A. Palma / 921 935 906 / 951 962 371 / dionisiopalma00@gmail.com

2023/2024
3𝑥+1
2 EXEMPLO 1:Considere a função 𝑦 = 𝑥+2
e determine nos termos da
3𝑥+1
definição, segundo Heine, o lim .
𝑥→3 𝑥+2
Resolução:
Consideremos uma sucessão qualquer de valores de 𝑥 que tende para 3. Por exemplo:
3 3𝑛
𝑥1 = 2 , 𝑥2 = 2 , … , 𝑥𝑛 = 𝑛+1…
Se substituirmos estes valores na função dada obtemos uma sucessão de valores de 𝑦,

cujo limite será o valor pedido. Assim temos:
3 3𝑛
3∙( )+1 3∙2+1 3( )+1
2 𝑛+1
𝑦1 = 3 , 𝑦2 = , … , 𝑦𝑛 = 3𝑛 …
+2 2+2 +2
2 𝑛+1
3𝑛 9𝑛+𝑛+1
3( )+1 10𝑛+1
𝑛+1
Como, lim 𝑦𝑛 = lim 3𝑛 = lim 𝑛+1
3𝑛+2𝑛+2 = lim =2
𝑛→∞ 𝑛→∞ 𝑛+1
+2 𝑛→∞ 𝑛+1
𝑛→∞ 5𝑛+2
3𝑥+1
Portanto, lim = 2.
𝑥→3 𝑥+2
EXEMPLO 2: Aplicando a definição de limite segundo Cauchy, mostre

que lim 2𝑥 + 3 = 5
𝑥→1
Resolução:
lim 2𝑥 + 3 = 5 ⟺ ∀𝜖 > 0, ∃𝛿 > 0?/ se 0 < |𝑥 − 1| < 𝛿 ⟹ |𝑓(𝑥) − 5| < 𝜖.

𝑥→1
Como, |𝑓(𝑥) − 5| = |2𝑥 + 3 − 5| = |2𝑥 − 2| = |2(𝑥 − 1)| = |2| ∙ |𝑥 − 1| =
𝜖
= 2|𝑥 − 1| < 𝜖 ⟺ |𝑥 − 1| < 2 = 𝛿.
𝜖
Logo, dado 𝜖 > 0, tomamos 𝛿 = 2 , temos:
𝜖 𝜖
Se 0 < |𝑥 − 1| < 𝛿 = 2 ⟹ |𝑓(𝑥) − 5| = 2|𝑥 − 1| < 2 (2) = 𝜖 ⟹ |𝑓(𝑥) − 5| < 𝜖
Portanto, lim 2𝑥 + 3 = 5.
𝑥→1

2023/2024
3
1.2 Operações com Limites (Propriedades dos Limites)
Supondo que 𝑘 é uma constante e 𝑛 um número inteiro positivo, se
os limites de 𝑓(𝑥) e 𝑔(𝑥) existem quando 𝑥 → 𝑎, então valem as
seguintes operações:
1. Constante
lim 𝑘 = 𝑘
𝑥→𝑎
2. Múltiplo Constante
lim [𝑘 ∙ 𝑓(𝑥)] = 𝑘 ∙ lim 𝑓(𝑥)

𝑥→𝑎 𝑥→𝑎
3. Adição
lim [𝑓(𝑥) ± 𝑔(𝑥)] = lim 𝑓(𝑥) ± lim 𝑔(𝑥)

𝑥→𝑎 𝑥→𝑎 𝑥→𝑎
4. Multiplicação
lim [𝑓(𝑥) ∙ 𝑔(𝑥)] = lim 𝑓(𝑥) ∙ lim 𝑔(𝑥)

5. Divisão
lim 𝑓(𝑥)
𝑓(𝑥) 𝑥→𝑎
lim = , lim 𝑔(𝑥) ≠ 0
𝑥→𝑎 𝑔(𝑥) lim 𝑔(𝑥) 𝑥→𝑎
𝑥→𝑎
6. Potência
𝑛
lim [𝑓(𝑥)]𝑛 = [lim 𝑓(𝑥)]
7. Radical
𝑛
lim √𝑓(𝑥) = 𝑛√ lim 𝑓(𝑥)
8. Logaritmo
lim [ln 𝑓(𝑥)] = ln [lim 𝑓(𝑥)]

{ , lim 𝑓(𝑥) > 0
∗ 𝑥→𝑎
lim [log 𝑘 𝑓(𝑥)] = log 𝑘 [lim 𝑓(𝑥)] , 𝑒𝑚 𝑞𝑢𝑒 𝑘 ∈ ℝ+ − {𝟏}
9. lim cos(𝑓(𝑥)) = cos (lim 𝑓(𝑥))


2023/2024
4 10. lim sen(𝑓(𝑥)) = sen (lim 𝑓(𝑥))

lim 𝑓(𝑥)
11. lim ef(x) = e𝑥→𝑎
𝑥→𝑎
12. lim 𝑃(𝑥) = 𝑃(𝑎), sendo 𝑃(𝑥) um polinómio.

𝑥→𝑎
1.3 Símbolos de Indeterminação
∞
1.
∞
0
2.
0
3. ∞ − ∞
4. 1∞
5. 0 × ∞
6. ∞0
7. 00
1.4 Algumas Operações Determinadas

Sendo 𝑘 um número real, temos as seguintes operações
determinadas:
I. Adição e Subtracção
a) ±𝑘 + ∞ = ∞
b) ±𝑘 − ∞ = −∞
c) +∞ + ∞ = ∞
d) −∞ − ∞ = −∞
II. Multiplicação
a) 𝑘 × (±∞) = ±∞, 𝑘 > 0
b) 𝑘 × (±∞) = ∓∞, 𝑘 < 0
c) (+∞) × (+∞) = +∞
d) (−∞) × (−∞) = +∞
e) (−∞) × (+∞) = −∞

2023/2024
III. Divisão
5
𝑘
a) = 0, ∀𝑘 ∈ ℝ
±∞
±𝑘
b) = ±∞, 𝑘 ≠ 0
0
0
c) = 0, 𝑘 ≠ 0
𝑘
±∞
d) = ±∞, 𝑘 > 0
𝑘
±∞
e) = ∓∞, 𝑘 < 0
𝑘
IV. Potência e Exponencial
a) 𝑘 0 = 1, 𝑘≠0
b) ∞𝑘 = ∞, 𝑘 > 0
c) ∞𝑘 = 0, 𝑘<0
d) 𝑘 +∞ = ∞, |𝑘| > 1
e) 𝑘 −∞ = 0, |𝑘| > 1
f) 𝑘 ∞ = 0, 0<𝑘<1
g) (−∞)𝑛 = −∞, 𝑛 ∈ ℕ, ímpar e 𝑛 ≠ 0
h) (−∞)𝑛 = +∞, 𝑛 ∈ ℕ, par e 𝑛 ≠ 0

V. Radiciação
a) 𝒏√+∞ = +∞, ∀𝑛 ∈ ℕ e 𝑛 ≥ 2
𝒏
b) √−∞ = −∞, ∀𝑛 ∈ ℕ, ímpar e 𝑛 ≥ 3
𝑎 ∞
𝒂 𝒙 𝒂 ∞
𝑠𝑒 𝑎 > 𝑏, (𝑏) = ∞
NOTA: 𝐥𝐢𝐦 (𝒃) = (𝒃) = { 𝑎 ∞
𝒙→∞
𝑠𝑒 𝑎 < 𝑏, (𝑏) = 0
OBSERVAÇÃO: Se 𝑓(𝑥) = 𝑃(𝑥) = Polinómio em x. Então, com
𝑓(𝑥) = 𝑃(𝑥) = 𝑎𝑛 𝑥 𝑛 + 𝑎𝑛−1 𝑥 𝑛−1 + ⋯ + 𝑎2 𝑥 2 + 𝑎1 𝑥 + 𝑎0 , vem:

lim 𝑓(𝑥) = lim 𝑃(𝑥) = 𝑎𝑛 𝑥 𝑛
𝑥→±∞ 𝑥→±∞
EXEMPLO 3:
3 ∙ (+∞)5 = +∞
lim 3𝑥 5 + 2𝑥 2 + 𝑥 + 1 = lim 3𝑥 5
𝑥→±∞ 𝑥→±∞
3 ∙ (−∞)5 = −∞

2023/2024
6
1.5 Produtos Notáveis (Identidades Algébricas Notáveis)
1. 𝑎2 − 𝑏 2 = (𝑎 − 𝑏)(𝑎 + 𝑏)
2. 𝑎3 − 𝑏 3 = (𝑎 − 𝑏)(𝑎2 + 𝑎𝑏 + 𝑏 2 )
3. 𝑎3 + 𝑏 3 = (𝑎 + 𝑏)(𝑎2 − 𝑎𝑏 + 𝑏 2 )
4. 𝑎4 − 𝑏 4 = (𝑎2 − 𝑏 2 )(𝑎2 + 𝑏 2 ) = (𝑎 − 𝑏)(𝑎 + 𝑏)(𝑎2 + 𝑏 2 )
5. (𝑎 + 𝑏)2 = 𝑎2 + 2𝑎𝑏 + 𝑏 2
6. (𝑎 − 𝑏)2 = 𝑎2 − 2𝑎𝑏 + 𝑏 2
7. (𝑎 − 𝑏)3 = 𝑎3 − 3𝑎2 𝑏 + 3𝑎𝑏 2 − 𝑏 3
8. (𝑎 + 𝑏)3 = 𝑎3 + 3𝑎2 𝑏 + 3𝑎𝑏 2 + 𝑏 3
1.6 Limites Laterais
Se 𝑥 < 𝑎, convencionalmente, escreve-se 𝑥 → 𝑎− ; por analogia, se

𝑥 > 𝑎, expressa-se da seguinte forma: 𝑥 → 𝑎+ .
Os números 𝑓(𝑎− ) = lim− 𝑓(𝑥) e 𝑓(𝑎+ ) = lim+ 𝑓(𝑥), chamam-se,

respectivamente, limite à esquerda da função 𝑓(𝑥) no ponto 𝒂, e

limite à direita da função 𝑓(𝑥) no ponto 𝒂.
Para a existência do limite da função 𝒇(𝒙), sendo 𝒙 → 𝒂, é

necessário e suficiente que exista a igualdade:
𝒇(𝑎− ) = 𝒇(𝑎+ ) ⇔ 𝐥𝐢𝐦− 𝒇(𝒙) = 𝐥𝐢𝐦+ 𝒇(𝒙).

𝒙→𝒂 𝒙→𝒂
Nota: Se 𝐥𝐢𝐦− 𝒇(𝒙) ≠ 𝐥𝐢𝐦+ 𝒇(𝒙), então não existe 𝐥𝐢𝐦 𝒇(𝒙).
𝒙→𝒂 𝒙→𝒂 𝒙→𝒂

2023/2024
7 Notações
Os limites laterais indicam-se da seguinte forma:
 Limite à esquerda de a:
lim 𝑓(𝑥) ou lim 𝑓(𝑥)
𝑥→𝑎−𝜀
𝑥→𝑎−
𝜀→0
 Limite à direita de a:
lim 𝑓(𝑥) ou lim 𝑓(𝑥)

𝑥→𝑎+𝜀
𝑥→𝑎+
𝜀→0
EXEMPLO 4:
𝑥+2 , 𝑠𝑒 𝑥 ≤ 2
1. Seja 𝑓(𝑥) = { , determine o lim 𝑓(𝑥).
2−𝑥 , 𝑠𝑒 𝑥 > 2 𝑥→2
Resolução:
∃ lim 𝑓(𝑥) ⟺ lim− 𝑓(𝑥) = lim+ 𝑓(𝑥)

𝑥→2 𝑥→2 𝑥→2
lim 𝑓(𝑥) = lim−(𝑥 + 2) = 2 + 2 = 4

𝑥→2− 𝑥→2
lim 𝑓(𝑥) = lim+(2 − 𝑥) = 2 − 2 = 0

𝑥→2+ 𝑥→2
Como, lim− 𝑓(𝑥) ≠ lim+ 𝑓(𝑥) logo, lim 𝑓(𝑥) não existe.
𝑥→2 𝑥→2 𝑥→2
|𝑥|
2. Verifique a existência do limite da função 𝑓(𝑥) = no
𝑥
ponto 𝑥 = 0.
Resolução:
−𝒙, 𝒔𝒆 𝒙 < 𝟎
Recorde que: |𝒙| = {
𝒙, 𝒔𝒆 𝒙 ≥ 𝟎
∃ lim 𝑓(𝑥) ⟺ lim− 𝑓(𝑥) = lim+ 𝑓(𝑥).
𝑥→0 𝑥→0 𝑥→0
−𝑥
lim− 𝑓(𝑥) = lim− = −1
𝑥→0 𝑥→0 𝑥
𝑥
lim+ 𝑓(𝑥) = lim+ 𝑥 = 1
𝑥→0 𝑥→0
Como, lim− 𝑓(𝑥) ≠ lim+ 𝑓(𝑥) logo, lim 𝑓(𝑥) não existe.
𝑥→0 𝑥→0 𝑥→0

2023/2024
𝑥 2 − 5, 𝑠𝑒 𝑥 < 3
8 3. Seja 𝑓(𝑥) = { , determine o lim 𝑓(𝑥).
√𝑥 + 13, 𝑠𝑒 𝑥 ≥ 3 𝑥→3
Resolução:
∃ lim 𝑓(𝑥) ⟺ lim− 𝑓(𝑥) = lim+ 𝑓(𝑥).

𝑥→3 𝑥→3 𝑥→3
lim 𝑓(𝑥) = lim−(𝑥 2 − 5) = 9 − 5 = 4

𝑥→3− 𝑥→3
lim 𝑓(𝑥) = lim+ √𝑥 + 13 = √3 + 13 = √16 = 4

𝑥→3+ 𝑥→3
Como, lim− 𝑓(𝑥) = lim+ 𝑓(𝑥) logo, existe lim 𝑓(𝑥) = 4.

𝑥→3 𝑥→3 𝑥→3
Obs.: Devemos recorrer aos limites laterais quando ao procurarmos 𝑥→𝑎

lim 𝑓(𝑥) se obtém:
a) Um limite infinito.
0
b) A indeterminação 0 (em certos casos).
c) A função seja definida por mais de uma expressão analítica (função definida em
ramo).
|𝑥|
d) A função seja revestida de aspectos especiais como: 𝑓(𝑥) = .
𝑥
1.7 Cálculo de limites indeterminados
 Ao calcular-se o limite da razão de dois polinómios

inteiros em relação a 𝑥, quando 𝑥 → ∞, é útil dividir
previamente em 𝑥 𝑛 (variável de maior grau) ambos os
membros da razão, onde 𝑛 é a potência máxima destes
polinómios.
 Tal método pode ser empregado, também, em muitos casos
para fracções, que contêm expressões irracionais.
 Ao calcular-se o limite da razão de dois polinómios
inteiros em relação a 𝑥, quando 𝑥 → 𝒂, isto quer dizer
que, a fracção (razão) tem pelo menos um fator comum no
numerador e no denominador que é da forma (𝑥 − 𝒂), onde 𝒂
é a tendência do limite.

2023/2024
9  As expressões irracionais se reduzem, em muitos casos, à

forma racional através da introdução de uma nova variável
(quando 𝑥 → 𝒂).
 Outro método, através do qual pode-se encontrar o limite,
a partir de uma expressão irracional, é o transporte do
conjugado da parte irracional do numerador para o
denominador, ou ao contrário, do denominador para o
numerador (quando 𝑥 → 𝒂).
 O método acima, também aplica-se nos limites de
expressões irracionais quando 𝑥 → ∞
∞
 Levantamento de indeterminação do tipo
∞
EXEMPLO 5:
0
𝑥 3 +5𝑥 ∞
1. lim = ∞ (𝑖𝑛𝑑. )
𝑥→∞ 2𝑥 3 −𝑥 2 +4
𝑥 3 5𝑥 5
𝑥 3 + 5𝑥 𝑥 3 + 𝑥3 1+ 2
𝑥 1+0 𝟏
lim 3 = lim = lim = =
𝑥→∞ 2𝑥 − 𝑥 2 + 4 𝑥→∞ 2𝑥 3 𝑥2 4 1 4
2−𝑥+ 3 2−0+0 𝟐
𝑥→∞
3 − 3+ 3 𝑥
𝑥 𝑥 𝑥
0 0
𝑥 ∞
2. lim = ∞ (𝑖𝑛𝑑. )
𝑥→∞ √𝑥 2 +1
𝑥
𝑥 𝑥 1 1 1 1
lim = lim = lim = lim = = =𝟏
𝑥→∞ √𝑥 2 + 1 𝑥→∞ √𝑥 2 + 1 1
√1 + 12 √1
𝑥→∞ 𝑥 2 𝑥→∞
√ 2 + 12
𝑥 𝑥 𝑥 𝑥

2023/2024
𝟎
10  Levantamento de indeterminação do tipo
𝟎
𝑥 4 −2𝑥+1 1−2+1 0
1. lim 𝑥 3 +3𝑥 2 +1 = 1+3+1 = 5 = 𝟎
𝑥→1
𝑥 2 +2𝑥−3 1−2−3 −4 𝟒
2. lim = = −7 = 𝟕
𝑥→−1 4𝑥−3 −4−3
𝑥 2 −𝑥+6 4−2+6 8
3. lim = =0=∞ NOTA:
𝑥→2 𝑥−2 2−2
Calculemos os limites laterais: 𝑥 2 − 𝑥 + 6 22 − 2 + 6

lim− = =
𝑥→2 𝑥−2 2− − 2
𝑥2 − 𝑥 + 6 (2 − 𝜀)2 − (2 − 𝜀) + 6
lim = lim = 𝟖
𝑥→2−𝜀 𝑥−2 𝜀→0 2−𝜀−2 = = −∞
𝜀→0 𝟎−
4 − 4𝜀 + 𝜀 2 − 2 + 𝜀 + 6 𝜀 2 − 3𝜀 + 8 8 𝑥 2 − 𝑥 + 6 22 − 2 + 6
= lim = lim = = −∞ lim = =
𝜀→0 −𝜀 𝜀→0 −𝜀 −0 𝑥→2+ 𝑥−2 2+ − 2
𝟖
𝑥2 − 𝑥 + 6 (2 + 𝜀)2 − (2 + 𝜀) + 6 = = +∞
lim = lim = 𝟎+
𝑥→2+𝜀 𝑥−2 𝜀→0 2+𝜀−2
𝜀→0
4 + 4𝜀 + 𝜀 2 − 2 − 𝜀 + 6 𝜀 2 + 3𝜀 + 8 8
= lim = lim = = +∞
𝜀→0 𝜀 𝜀→0 𝜀 0
Como os limites à esquerda e à direita de 𝟐 são diferentes,

𝑥 2 −𝑥+6
então não exite lim .
𝑥→2 𝑥−2
𝑥 2 +5𝑥+4 0
4. lim = 0 (𝑖𝑛𝑑.)
𝑥→−4 𝑥 2 +3𝑥−4
𝑥 2 + 5𝑥 + 4 (𝑥 + 4)(𝑥 + 1) 𝑥 + 1 −4 + 1 𝟑
lim 2 = lim = lim = =
𝑥→−4 𝑥 + 3𝑥 − 4 𝑥→−4 (𝑥 + 4)(𝑥 − 1) 𝑥→−4 𝑥 − 1 −4 − 1 𝟓
2𝑥 3 +𝑥 2 −4𝑥+1 0
5. lim 𝑥 3 −3𝑥 2 +5𝑥−3 = 0 (𝑖𝑛𝑑. )
𝑥→1
2𝑥 3 + 𝑥 2 − 4𝑥 + 1 (𝑥 − 1)(2𝑥 2 + 3𝑥 − 1) 2𝑥 2 + 3𝑥 − 1
lim = lim = lim 2 =
𝑥→1 𝑥 3 − 3𝑥 2 + 5𝑥 − 3 𝑥→1 (𝑥 − 1)(𝑥 2 − 2𝑥 + 3) 𝑥→1 𝑥 − 2𝑥 + 3
2+3−1 4
= = =𝟐
1−2+3 2
3𝑥 3 −4𝑥 2 −𝑥+2 0
6. lim = 0 (𝑖𝑛𝑑. )
𝑥→1 2𝑥 3 −3𝑥 2 +1
3𝑥 3 − 4𝑥 2 − 𝑥 + 2 (𝑥 − 1)2 (3𝑥 + 2) 3𝑥 + 2 𝟓
lim = lim = =
𝑥→1 2𝑥 3 − 3𝑥 2 + 1 𝑥→1 (𝑥 − 1)2 (2𝑥 + 1) 2𝑥 + 1 𝟑

2023/2024
√1+𝑥 − 2 0
11 7. lim = (𝑖𝑛𝑑. )
𝑥→3 𝑥−3 0
2
√1+𝑥 – 2 (√1+𝑥 −2)(√1+𝑥 +2) (√1+𝑥) − 22
Lim 𝑥−3 = lim (𝑥−3)(√1+𝑥 +2)
= lim (𝑥−3)( =
𝑥→3 𝑥→3 𝑥→3 √1+𝑥 +2)
1+𝑥−4 𝑥−3 1 𝟏
= lim (𝑥−3)( = lim (𝑥−3)( = lim =𝟒
𝑥→3 √1+𝑥 +2) 𝑥→3 √1+𝑥 +2) 𝑥→3 √1+𝑥 +2
√𝑥 − 1 0
8. lim = 0 (𝑖𝑛𝑑. )
𝑥→1 √2𝑥+3 − √5
√𝑥 − 1 (√𝑥 − 1)(√𝑥 + 1)(√2𝑥 + 3 + √5)

lim = lim =
𝑥→1 √2𝑥 + 3 − √5 𝑥→1 (√2𝑥 + 3 − √5)(√2𝑥 + 3 + √5)(√𝑥 + 1)
(𝑥 − 1)(√2𝑥 + 3 + √5) (𝑥 − 1)(√2𝑥 + 3 + √5)
= lim = lim =
𝑥→1 (2𝑥 + 3 − 5)(√𝑥 + 1) 𝑥→1 (2𝑥 − 2)(√𝑥 + 1)
(𝑥 − 1)(√2𝑥 + 3 + √5) √2𝑥 + 3 + √5 2√5 √𝟓

= lim = lim = =
𝑥→1 2(𝑥 − 1)(√𝑥 + 1) 𝑥→1 2(√𝑥 + 1) 4 𝟐
3 3
√𝑥 − √2 0
9. lim = 0 (𝑖𝑛𝑑. )
𝑥→2 𝑥−2
3 3 3 3 3 3 3
√𝑥 − √2 ( √𝑥 − √2)( √𝑥 2 + √2𝑥 + √22 )
lim = lim =
𝑥→2 𝑥−2 𝑥→2 3 3 3
(𝑥 − 2)( √𝑥 2 + √2𝑥 + √22 )
3 3
√𝑥 3 − √23 𝑥−2
= lim 3 3 3 = lim 3 3 3 =
𝑥→2 (𝑥 − 2)( √𝑥 2 + √2𝑥 + √22 ) 𝑥→2 (𝑥 − 2)( √𝑥 2 + √2𝑥 + √22 )
𝟑
1 √𝟐 1 1
= lim 3 = = =
3
𝑥→2 √𝑥 2 + 3√2𝑥 + √22 3 3 3 3
√4 + √4 + √4 3√4 𝟔
(3−𝑥)4 − 16 0
10. lim = 0 (𝑖𝑛𝑑. )
𝑥→1 𝑥3 −1
(3 − 𝑥)4 − 16 (1 − 𝑥)(5 − 𝑥)((3 − 𝑥)2 + 4)

lim = lim =
𝑥→1 𝑥3 − 1 𝑥→1 (𝑥 − 1)(𝑥 2 + 𝑥 + 1)
−(𝑥 − 1)(5 − 𝑥)((3 − 𝑥)2 + 4) −(5 − 𝑥)((3 − 𝑥)2 + 4)
= lim = lim =
𝑥→1 (𝑥 − 1)(𝑥 2 + 𝑥 + 1) 𝑥→1 𝑥2 + 𝑥 + 1
−(5 − 1)(22 + 4) 𝟑𝟐
= =−
1+1+1 𝟑
 Levantamento de indeterminação do tipo ∞ − ∞
1. lim √𝑥 + 3 − √𝑥 = ∞ − ∞ (𝑖𝑛𝑑. )
𝑥→∞
(√𝑥 + 3 − √𝑥)(√𝑥 + 3 + √𝑥)

lim √𝑥 + 3 − √𝑥 = lim =
𝑥→∞ 𝑥→∞ √𝑥 + 3 + √𝑥

2023/2024
2 2
12 (√𝑥 + 3) − (√𝑥) 𝑥+3−𝑥 3
= lim = lim = lim =
𝑥→∞ √𝑥 + 3 + √𝑥 𝑥→∞ √𝑥 + 3 + √𝑥 𝑥→∞ √𝑥 + 3 + √𝑥
3 3 3
= = = =𝟎
√∞ + 3 + √ ∞ ∞ + ∞ ∞
2. lim √𝑥 2 − 5𝑥 + 4 − 𝑥 = ∞ − ∞ (𝑖𝑛𝑑. )
𝑥→∞
(√𝑥 2 − 5𝑥 + 4 − 𝑥)(√𝑥 2 − 5𝑥 + 4 + 𝑥)
lim √𝑥 2 − 5𝑥 + 4 − 𝑥 = lim =
𝑥→∞ 𝑥→∞ √𝑥 2 − 5𝑥 + 4 + 𝑥
𝑥 2 − 5𝑥 + 4 − 𝑥 2 −5𝑥 + 4
= lim = lim =
𝑥→∞ √𝑥 2− 5𝑥 + 4 + 𝑥 𝑥→∞ √𝑥 2
− 5𝑥 + 4 + 𝑥
5𝑥 4 4
− 𝑥 +𝑥 −5 + 𝑥 𝟓
= lim = lim =−
𝑥→∞ 𝑥 2 𝑥→∞ 𝟐
√ 2 − 5𝑥2 + 42 + 𝑥 √1 − 5 + 42 + 1
𝑥 𝑥 𝑥 𝑥 𝑥 𝑥
 Levantamento de indeterminação do TIPO 1∞ :

Exercícios que podem ser resolvidos com auxílio dos limites
fundamentais (Limites Notáveis):
𝟏 𝒙
1) 𝐥𝐢𝐦 (𝟏 + ) = 𝒆, (sendo 𝑒 (𝐸𝑢𝑙𝑒𝑟) a base do logaritmo
𝒙→±∞ 𝒙
neperiano (natural) 𝑒 = 𝟐, 𝟕𝟏𝟖 …)

𝑘 𝑥
2) lim (1 + ) = 𝑒 𝑘
𝑥→±∞ 𝑥
𝟏
3) 𝐥𝐢𝐦(𝟏 + 𝒙) = 𝒆 𝒙
𝒙→𝟎
1
4) lim (1 + 𝑘𝑥 )𝑥 = 𝑒 𝑘
𝑥→0

2023/2024
13
EXEMPLO 6:
8 𝑥
1. lim (1 + 𝑥) = 1∞ (𝑖𝑛𝑑. )
𝑥→∞
1ª via:
8
𝑥 𝑥∙𝑥
𝑥
8 8 8 lim
8𝑥
lim (1 + ) = lim [(1 + ) ] = 𝑒 𝑥→∞ 𝑥 = 𝑒 8
𝑥→∞ 𝑥 𝑥→∞ 𝑥
8 𝑥
lim (1 + ) = 1∞ (𝑖𝑛𝑑. )
𝑥→∞ 𝑥
2ª via:
8 8
Fazendo = 𝑦 ⇒ 𝑥 = 𝑦, quando 𝑥 → ∞, 𝑦 → 0. Então: 1
𝑥
Nota: lim (1 + 𝑦)𝑦 = 𝑒
8
𝑦→0
8 1
8 𝑥 8
lim (1 + 𝑥) = lim (1 + 𝑦) = lim [(1 + 𝑦) ] = 𝑒
𝑦 𝑦
𝑥→∞ 𝑦→0 𝑦→0
8 𝑥
lim (1 + 𝑥) = 1∞ (𝑖𝑛𝑑. )
𝑥→∞
3ª via:
8 1
Fazendo = 𝑦 ⇒ 𝑥 = 8𝑦, quando 𝑥 → ∞, 𝑦 → ∞. Então:
𝑥
1 𝑦
8
Nota: lim (1 + ) = 𝑒
8 𝑥 1 8𝑦 1 𝑦 𝑦→∞ 𝑦
lim (1 + 𝑥) = lim (1 + 𝑦) = lim [(1 + 𝑦) ] = 𝑒 8
𝑥→∞ 𝑦→∞ 𝑦→∞
1 𝑥
2. lim (1 + 2𝑥) = 1∞ (𝑖𝑛𝑑. )
𝑥→∞
1
∙𝑥
1 𝑥 1 2𝑥 2𝑥 lim
𝑥 1
lim (1 + ) = lim [(1 + ) ] = 𝑒 𝑥→∞2𝑥 = 𝑒 2 = √𝑒
𝑥→∞ 2𝑥 𝑥→∞ 2𝑥

2023/2024
1 𝑥+2
14 3. lim (1 + 𝑥) = 1∞ (𝑖𝑛𝑑. )
𝑥→∞
1 𝑥+2 1 𝑥 1 2
lim (1 + ) = lim (1 + ) ∙ lim (1 + ) = 𝑒 ∙ 1 = 𝑒
𝑥→∞ 𝑥 𝑥→∞ 𝑥 𝑥→∞ 𝑥
1 4−𝑥
4. lim (1 + 𝑥) = 1∞ (𝑖𝑛𝑑. )
𝑥→∞
1 4
1 4−𝑥 lim (1 + 𝑥) 1
𝑥→∞
lim (1 + ) = 𝑥 =
𝑥→∞ 𝑥 1 𝑒
lim (1 + 𝑥)
𝑥→∞
1 2𝑥
5. lim (1 + 𝑥) = 1∞ (𝑖𝑛𝑑. )
𝑥→∞
2
1 2𝑥 1 𝑥
lim (1 + ) = lim [(1 + ) ] = 𝑒 2
𝑥→∞ 𝑥 𝑥→∞ 𝑥
𝑥−1 𝑥
6. lim (𝑥+1) = 1∞ (𝑖𝑛𝑑. )
𝑥→∞
𝑥−1 𝑥 𝑥−1 𝑥
𝑥−1−𝑥−1 𝑥
lim ( ) = lim (1 + − 1) = lim (1 + ) =
𝑥→∞ 𝑥+1 𝑥→∞ 𝑥+1 𝑥→∞ 𝑥+1
−2
𝑥+1 𝑥+1 ∙ 𝑥
𝑥
−2 −2 −2 lim
−2𝑥 1
= lim (1 + ) = lim [(1 + ) ] = 𝑒 𝑥→∞ 𝑥+1 = 𝑒 −2 =
𝑥→∞ 𝑥+1 𝑥→∞ 𝑥+1 𝑒2

2023/2024
15 1.8 Limites notáveis de funções exponenciais e

logarítmicas
 Limite Exponencial Fundamental
𝟏 𝒙
𝐥𝐢𝐦 (𝟏 + 𝒙) = 𝒆, onde 𝒆 é o número irracional cujo valor aproximado é
𝒙→±∞
𝟐, 𝟕𝟏𝟖𝟐𝟖𝟏𝟖𝟐𝟖𝟒𝟓𝟗 ….
1
Teorema 1 : Seja a função 𝑓(𝑥) = (1 + 𝑥)𝑥 definida em {𝑥 ∈ ℝ: −1 < 𝑥 ≠ 0},
então:
1
lim(1 + 𝑥)𝑥 = 𝑒
𝑥→0
Demonstração:
1 1 𝑞𝑢𝑎𝑛𝑑𝑜 𝑥 → 0+ , 𝑢 → +∞
Supondo que 𝑥 = 𝑢 ⇒ 𝑥 = 𝑢, { , temos:
𝑞𝑢𝑎𝑛𝑑𝑜 𝑥 → 0− , 𝑢 → −∞
1 1 𝑢
lim (1 + 𝑥)𝑥
= lim (1 + ) = 𝑒
𝑥→0+ 𝑢→+∞ 𝑢
1 1 𝑢
lim−(1 + 𝑥) = lim (1 + ) = 𝑒
{𝑥→0
𝑥
𝑢→−∞ 𝑢
1
Portanto, lim(1 + 𝑥)𝑥 = 𝑒.
𝑥→0
𝑎𝑥 −1
Teorema 2 : Se 0 < 𝑎 ≠ 1, então temos que lim 𝑥
= ln 𝑎
𝑥→0
Demonstração:
Supondo que 𝑎 𝑥 − 1 = 𝑡 ⇒ 𝑎 𝑥 = 𝑡 + 1 ⇒ ln 𝑎 𝑥 = ln(𝑡 + 1) ⇒ 𝑥 ∙ ln 𝑎 = ln(𝑡 + 1) ⇒
ln(𝑡+1)
⇒𝑥= , quando 𝑥 → 0, 𝑡 → 0, temos:
ln 𝑎
𝑎𝑥 − 1 𝑡 𝑡 ∙ ln 𝑎 𝑡
lim = lim = lim = ln 𝑎 ∙ lim =
𝑥→0 𝑥 𝑡→0 ln(𝑡 + 1) 𝑡→0 ln(𝑡 + 1) 𝑡→0 ln(𝑡 + 1)
ln 𝑎
1 1 ln 𝑎
= ln 𝑎 ∙ lim = ln 𝑎 ∙ lim = =
𝑡→0 1 𝑡→0 1 1
𝑡 ∙ ln(𝑡 + 1) ln(𝑡 + 1) 𝑡 lim [ln(𝑡 +
𝑡→0
1) 𝑡 ]
ln 𝑎 ln 𝑎 ln 𝑎
= 1 = = = ln 𝑎
ln 𝑒 1
ln [lim(𝑡 + 1) 𝑡 ]
𝑡→0

2023/2024
𝑎𝑥 −1
16 Portanto, lim = ln 𝑎.
𝑥→0 𝑥
Observação: Quando 𝑎 = 𝑒 teremos que lim 𝑥→0

𝑒 𝑥 −1
𝑥
= ln 𝑒 = 1
𝑎 1
Nota 1: 𝑏 = 𝑏 ∙ 𝑎 Nota 4: 𝑛 ∙ ln 𝑥 = ln 𝑥 𝑛
𝑎 1 1
Nota 2: 𝑏 = 𝑏 =1 Nota 5: 𝑒 → 𝐸𝑢𝑙𝑒𝑟
∙𝑏
𝑎 𝑎
Nota 3: 𝑎 + 𝑏 = 𝑏 + 𝑎 Nota 6: ln 𝑒 = 1
Em resumo temos:
Limites Notáveis de Funções Exponenciais e
Logarítmicas
1 𝑥
 lim (1 + ) = 𝑒, (sendo 𝑒 (𝐸𝑢𝑙𝑒𝑟) a base do logaritmo neperiano
𝑥→±∞ 𝑥
(natural) 𝑒 = 2,718 …)
1
 lim (1 + 𝑥 ) = 𝑒 𝑥
𝑥→0
𝑎𝑥 −1
 lim = ln 𝑎
𝑥→0 𝑥
𝑒 𝑥 −1
 lim =1
𝑥→0 𝑥
ln(𝑥+1)
 lim =1
𝑥→0 𝑥
𝑒𝑥
 lim = +∞, (𝑝 ∈ ℝ)
𝑥→+∞ 𝑥 𝑝
ln 𝑥
 lim =0
𝑥→+∞ 𝑥

2023/2024
17
EXEMPLO 7: Calcule os seguintes limites:
8 𝑥
a) lim (1 + 𝑥) = 1∞ (𝑖𝑛𝑑. )
𝑥→∞
Resolução:
8 8
Fazendo 𝑥 = 𝑦 ⇒ 𝑥 = 𝑦 , quando 𝑥 → ∞, 𝑦 → 0. Então: 1
Nota: lim (1 + 𝑦)𝑦 = 𝑒
8
𝑦→0
8 1
8 𝑥
lim (1 + 𝑥) = lim (1 + 𝑦) = lim [(1 + 𝑦) ] = 𝑒 8
𝑦 𝑦
𝑥→∞ 𝑦→0 𝑦→0
Outra maneira de resolver o exercício
8 1
Fazendo 𝑥 = 𝑦 ⇒ 𝑥 = 8𝑦, quando 𝑥 → ∞, 𝑦 → ∞. Então:
1 𝑦
8
Nota: lim (1 + ) = 𝑒
8 𝑥 1 8𝑦 1 𝑦 𝑦→∞ 𝑦
lim (1 + 𝑥) = lim (1 + 𝑦) = lim [(1 + 𝑦) ] = 𝑒 8
𝑥→∞ 𝑦→∞ 𝑦→∞
√3𝑥 − 1 0
b) lim = 0 (𝑖𝑛𝑑. )
𝑥→0 𝑥
Resolução:
𝑥
√3𝑥 − 1 (√3) − 1
lim = lim = ln √3
𝑥→0 𝑥 𝑥→0 𝑥
𝑒 2𝑥 −𝑒 8𝑥 0
c) lim = 0 (𝑖𝑛𝑑. )
𝑥→0 3𝑥
Resolução:
𝑒 2𝑥 − 𝑒 8𝑥 𝑒 2𝑥 − 𝑒 8𝑥 − 1 + 1 (𝑒 2𝑥 − 1) + (−𝑒 8𝑥 + 1)
lim = lim = lim =
𝑥→0 3𝑥 𝑥→0 3𝑥 𝑥→0 3𝑥
(𝑒 2𝑥 − 1) − (𝑒 8𝑥 − 1)
= lim
𝑥→0 3𝑥
𝑒 2𝑥 − 1 𝑒 8𝑥 − 1
= lim − lim
𝑥→0 3𝑥 𝑥→0 3𝑥 𝑦
2𝑥 = 𝑦 ⇒ 𝑥 = 2 , 𝑞𝑢𝑎𝑛𝑑𝑜 𝑥 → 0, 𝑦 → 0
1 𝑒 2𝑥 −1 1 𝑒 8𝑥 −1 supondo que: { 𝑧
= 3 ∙ lim − 3 ∙ lim , 8𝑥 = 𝑧 ⇒ 𝑥 = 8 , 𝑞𝑢𝑎𝑛𝑑𝑜 𝑥 → 0, 𝑧 → 0
𝑥→0 𝑥 𝑥→0 𝑥
1 𝑒𝑦 − 1 1 𝑒𝑧 − 1
= ∙ lim 𝑦 − ∙ lim 𝑧
3 𝑦→0 3 𝑧→0
2 8

2023/2024
1 2(𝑒 𝑦 − 1) 1 8(𝑒 𝑧 − 1)
18 = ∙ lim − ∙ lim
3 𝑦→0 𝑦 3 𝑧→0 𝑧
=
2
∙ lim
𝑒𝑦 − 1 8
− ∙ lim
𝑒𝑧 − 1 Nota:
3 𝑦→0 𝑦 3 𝑧→0 𝑧
2 8
 𝑎 − 𝑏 = 𝑎 + (−𝑏)
= ∙1− ∙1
3 3  −𝑏 + 𝑎 = +(−𝑏 + 𝑎) = −(𝑏 − 𝑎)
2 8 𝑎−𝑏 1 𝑎−𝑏
= −  = ∙
3 3 𝑘𝑥 𝑘 𝑥
2−8 𝑎−𝑏 𝑘(𝑎−𝑏)
=  =
3 𝑥
𝑥
𝑘
6
= − = −𝟐
3
ln(𝑥+3)−ln 3 0
d) lim = 0 (𝑖𝑛𝑑. )
𝑥→0 𝑥
Resolução:
𝑥+3
ln(𝑥 + 3) − ln 3 ln ( 3 ) 1 𝑥+3
lim = lim = lim ∙ ln ( )=
𝑥→0 𝑥 𝑥→0 𝑥 𝑥→0 𝑥 3
1
𝑥+3 𝑥
= lim ln ( )
𝑥→0 3
1
𝑥+3 𝑥
= ln [lim ( ) ]
𝑥→0 3
1
𝑥 𝑥
= ln [lim ( + 1) ]
𝑥→0 3
1
𝑥 𝑥 𝑥
= ln [lim (1 + ) ], supondo que 3 = 𝑡 ⇒ 𝑥 = 3𝑡, 𝑞𝑢𝑎𝑛𝑑𝑜 𝑥 → 0, 𝑡 → 0
𝑥→0 3
1
= ln [lim(1 + 𝑡)3𝑡 ]
𝑡→0
1 Nota:
1 3
= ln [lim(1 + 𝑡) 𝑡 ] 𝑎+𝑏 𝑎 𝑏
𝑡→0
1
 = +
𝑘 𝑘 𝑘
= ln 𝑒 3 1
1
= ∙ ln 𝑒
 lim(1 + 𝑡) = 𝑒 𝑡
3 𝑡→0
1 𝑥
= ∙1  ln 𝑥 − ln 𝑦 = ln ( )
3 𝑦
𝟏  𝑎+𝑏 =𝑏+𝑎
=
𝟑

2023/2024
19 EXERCÍCIOS PROPOSTOS
1. Calcule os seguintes limites:
𝑒 𝑎𝑥 – 𝑒 𝑏𝑥
1.1 Lim
𝑥→0 𝑥
23𝑥 − 1
1.2 lim
𝑥→0 𝑥
7
√𝑒 𝑥 + 𝑥 − 1
1.3 lim
𝑥→0 2𝑥
𝑒 5𝑥 − 1
1.4 lim
𝑥→0 𝑥
𝑒 8𝑥 − 1
1.5 lim
𝑥→0 𝑥
5
1− √𝑒 𝑥
1.6 lim
𝑥→0 𝑥
𝑒 5𝑥 − 𝑒 4𝑥
1.7 lim
𝑥→0 𝑥
𝑒 7𝑥 − 𝑒 𝑥
1.8 lim
𝑥→0 3𝑥
𝑎𝑥 − 𝑏𝑥
1.9 lim , (𝑎, 𝑏 > 0)
𝑥→0 𝑥
22𝑥 −4∙2𝑥 + 3
1.10 lim
𝑥→0 2𝑥 −1
log(1+10𝑥)
1.11 lim
𝑥→0 𝑥
1.12 lim 𝑥[ln(𝑥 + 1) − ln 𝑥]

𝑥→+∞
1.13 lim [ln(2𝑥 + 1) − ln(𝑥 + 2)]

𝑥→+∞
1 2𝑥
1.14 lim (1 + 𝑥)
𝑥→∞
1 −𝑥
1.15 lim (1 + 𝑥)
𝑥→∞
1 3𝑥
1.16 lim (1 + 𝑥)
𝑥→∞
𝑥
1 −2
1.17 lim (1 + )
𝑥→∞ 𝑥
1 𝑥
1.18 lim (1 + 2𝑥)
𝑥→∞
1 2𝑥
1.19 lim (1 + 𝑥)
𝑥→∞

2023/2024
20 1.9 Limites de funções trigonométricas
Em muitos casos, ao calcularmos os limites, utilizamos a fórmula:
𝒔𝒆𝒏𝒙
𝐥𝐢𝐦 =𝟏
𝒙→𝟎 𝒙
e pressupõe-se que lim 𝑠𝑒𝑛𝑥 = 𝑠𝑒𝑛𝑎 e lim 𝑐𝑜𝑠𝑥 = 𝑐𝑜𝑠𝑎 sejam

conhecidos.
EXEMPLO 8:
𝑠𝑒𝑛3𝑥 0
1. lim = 0 (𝑖𝑛𝑑. )
𝑥→0 10𝑥
𝑠𝑒𝑛3𝑥 1 𝑠𝑒𝑛3𝑥 1 𝑠𝑒𝑛3𝑥 3 𝑠𝑒𝑛3𝑥 3 3

lim = ∙ lim = ∙ lim ∙3= ∙ lim = ∙1=
𝑥→0 10𝑥 10 𝑥→0 𝑥 10 𝑥→0 3𝑥 10 𝑥→0 3𝑥 10 10
𝑡𝑔𝑥 0
2. lim = 0 (𝑖𝑛𝑑. )
𝑥→0 𝑥
𝑠𝑒𝑛𝑥
𝑡𝑔𝑥 𝑠𝑒𝑛𝑥 𝑠𝑒𝑛𝑥 1
lim = lim 𝑐𝑜𝑠𝑥 = lim = lim ∙ lim =1∙1=1
𝑥→0 𝑥 𝑥→0 𝑥 𝑥→0 𝑥𝑐𝑜𝑠𝑥 𝑥→0 𝑥 𝑥→0 𝑐𝑜𝑠𝑥
𝑠𝑒𝑛5𝑥 0
3. lim 𝑠𝑒𝑛2𝑥 = 0 (𝑖𝑛𝑑. )
𝑥→0
𝑠𝑒𝑛5𝑥 𝑠𝑒𝑛5𝑥 𝑠𝑒𝑛5𝑥

𝑠𝑒𝑛5𝑥 5∙ lim
lim = lim 5𝑥 = ∙ lim 5𝑥 = ∙ 𝑥→0 5𝑥 = 5 ∙ 1 = 5
5 5
𝑥→0 𝑠𝑒𝑛2𝑥 𝑥→0 𝑠𝑒𝑛2𝑥 2 𝑥→0 𝑠𝑒𝑛2𝑥 2 𝑠𝑒𝑛2𝑥 2 1 2
2 ∙ 2𝑥 lim
2𝑥 𝑥→0 2𝑥
𝑠𝑒𝑛𝑘𝑥 0
4. lim = 0 (𝑖𝑛𝑑. )
𝑥→0 𝑥
NOTA:
𝑠𝑒𝑛𝑘𝑥 𝑠𝑒𝑛𝑘𝑥 𝑠𝑒𝑛𝑘𝑥 𝑎
lim = lim ∙ 𝑘 = 𝑘 ∙ lim =𝑘∙1=𝑘
𝑥→0 𝑥 𝑥→0 𝑘𝑥 𝑥→0 𝑘𝑥 𝑎 𝑦
a) = 𝑏
2𝑥 0
𝑏
5. lim 𝑠𝑒𝑛𝑥 = 0 (𝑖𝑛𝑑. ) 𝑦
𝑥→0 𝑥 1
b) = 𝑎
𝑎
2𝑥 2 lim 2 2 𝑥
lim = lim 𝑠𝑒𝑛𝑥 = 𝑥→0𝑠𝑒𝑛𝑥 1 = 2
=
𝑥→0 𝑠𝑒𝑛𝑥 𝑥→0 lim
𝑥 𝑥→0 𝑥

2023/2024
1−𝑐𝑜𝑠𝑥 0
21 6. lim = (𝑖𝑛𝑑. )
𝑥→0 𝑥 0
1 − 𝑐𝑜𝑠𝑥 (1 − 𝑐𝑜𝑠𝑥)(1 + 𝑐𝑜𝑠𝑥) 1 − 𝑐𝑜𝑠 2 𝑥

lim = lim = lim =
𝑥→0 𝑥 𝑥→0 𝑥(1 + 𝑐𝑜𝑠𝑥) 𝑥→0 𝑥(1 + 𝑐𝑜𝑠𝑥)
𝑠𝑒𝑛2 𝑥 𝑠𝑒𝑛𝑥 ∙ 𝑠𝑒𝑛𝑥 𝑠𝑒𝑛𝑥 𝑠𝑒𝑛𝑥

= lim = lim = lim ∙ lim =1∙0=0
𝑥→0 𝑥(1 + 𝑐𝑜𝑠𝑥) 𝑥→0 𝑥(1 + 𝑐𝑜𝑠𝑥) 𝑥→0 𝑥 𝑥→0 (1 + 𝑐𝑜𝑠𝑥)
EXERCÍCIOS PROPOSTOS
1. Calcule os seguintes limites:

1.1 Lim 𝑥 ∙ 𝑐𝑜𝑠𝑠𝑒𝑐𝑥
𝑥→0
1−𝑐𝑜𝑠𝑥
1.2 lim
𝑥→0 𝑥2
𝑠𝑒𝑛2 𝑥
1.3 lim 1−𝑐𝑜𝑠𝑥
𝑥→0
𝑠𝑒𝑐𝑥−𝑐𝑜𝑠𝑥
1.4 lim
𝑥→0 𝑥2
1−√𝑐𝑜𝑠𝑥
1.5 lim
𝑥→0 𝑥2
𝑡𝑔𝑥−𝑠𝑒𝑛𝑥
1.6 lim
𝑥→0 𝑥3

2023/2024
22 Alguns infinitésimos equivalentes, quando 𝑥 → 0
1. 𝑙𝑖𝑚 𝑒 𝑥 − 1 ≈ 𝑥
𝑥→0
2. 𝑙𝑖𝑚 𝑎 𝑥 − 1 ≈ 𝑥 𝑙𝑛 𝑎 , (𝑎 > 0 e 𝑎 ≠ 1)
𝑥→0
3. 𝑙𝑖𝑚 𝑠𝑒𝑛𝑥 ≈ 𝑥
𝑥→0
𝑥2
4. 𝑙𝑖𝑚 1 − 𝑐𝑜𝑠𝑥 ≈
𝑥→0 2
5. 𝑙𝑖𝑚 𝑡𝑔𝑥 ≈ 𝑥
𝑥→0
6. 𝑙𝑖𝑚 𝑎𝑟𝑐𝑠𝑒𝑛𝑥 ≈ 𝑥
𝑥→0
7. 𝑙𝑖𝑚 𝑎𝑟𝑐𝑡𝑔𝑥 ≈ 𝑥
𝑥→0
8. 𝑙𝑖𝑚 𝑙𝑛(1 ± 𝑥) ≈ ±𝑥
𝑥→0
𝑛 𝑥
9. 𝑙𝑖𝑚 √1 + 𝑥 − 1 ≈
𝑥→0 𝑛
1
10. 𝑙𝑖𝑚 − 1 ≈ ±𝑥
𝑥→0 1±𝑥
EXEMPLO 9:
𝑒 8𝑥 − 1 0
lim = 0 (ind.) NOTA: 𝑙𝑖𝑚 𝑒 8𝑥 − 1 ≈ 8𝑥
𝑥→0 𝑥
𝑥→0
𝑒 8𝑥 − 1 8𝑥
lim = lim =8
𝑥→0 𝑥 𝑥→0 𝑥

2023/2024
23 1.10 Assímptotas
Uma assímptota é uma recta na qual o gráfico da funcão se

aproxima à medida que a variável independente (𝒙) ou a variável
dependente (𝒚) se aproxima de um determinado valor. Ou seja são
rectas que tangenciam o gráfico de uma funcão no infinito e,
normalmente são paralelas aos eixos de 𝑥 e 𝑦. Isto é, estes mesmos
eixos também podem ser assímptotas.
𝐀𝐬𝐬í𝐦𝐩𝐭𝐨𝐭𝐚 𝐯𝐞𝐫𝐭𝐢𝐜𝐚𝐥 (AV)

Classificação das assímptotas:{ Assímptota horizontal (AH)
𝐀𝐬𝐬í𝐦𝐩𝐭𝐨𝐭𝐚 𝐧ã𝐨 𝐯𝐞𝐫𝐭𝐢𝐜𝐚𝐥 (ANV) {
Assímptota oblíqua (AO)
 Assímptota vertical
A recta 𝑥 = 𝑎 é uma assímptota vertical da curva C: 𝑦 = 𝑓(𝑥) se

cumprir a relacão seguinte:
lim 𝑓(𝑥 ) = ∞.
𝑥→𝑎
 Passos para a sua determinação:
1º. Determinar o domínio da função (𝑫𝒇 )
Situações onde AV existe
 Se 𝑫𝒇 = ℝ ∖ {𝒂} existe AV: lim 𝑓(𝑥) = ±∞, então 𝒙 = 𝒂 é AV.

𝑥→𝑎
 Se 𝑫𝒇 = ]𝒂; +∞[ existe AV: lim+ 𝑓(𝑥) = ±∞, então 𝒙 = 𝒂 é AV.

𝑥→𝑎
 Se 𝑫𝒇 = ]−∞; 𝒂[ existe AV: lim− 𝑓(𝑥) = ±∞, então 𝒙 = 𝒂 é AV.

𝑥→𝑎
Nota: Se 𝑥→𝑎
lim± 𝑓(𝑥) = 𝑘, onde 𝑘 ∈ ℝ, não existe AV e, 𝑷(𝒂; 𝒌) é um ponto de
descontinuidade.

2023/2024
24
Situações onde AV não existe
 Se 𝑫𝒇 = ℝ, não existe AV.
 Se 𝑫𝒇 = [𝒂; +∞[, não existe AV.
 Se 𝑫𝒇 = ]−∞; 𝒂], não existe AV.
 Assímptota horizontal
A recta 𝑦 = 𝑏 é uma assímptota horizontal da C: 𝑦 = 𝑓(𝑥) se cumprir

a relacão seguinte:
𝐥𝐢𝐦 𝒇(𝒙) = 𝒃, onde 𝒃 ∈ ℝ

𝒙→±∞
 Assímptota não vertical
A forma prática de encontrar as assímptotas oblíqua (horizontal)
de uma curva C: 𝑦 = 𝑓(𝑥) é da maneira seguinte:
Se existem os limites,
𝑓(𝑥)
lim =𝑚 e lim [𝑓(𝑥 ) − 𝑚𝑥 ] = 𝑏
𝑥→±∞ 𝑥 𝑥→±∞
A recta 𝒚 = 𝒎𝒙 + 𝒃 é uma assímptota oblíqua. E, é horizontal
quando 𝑚 = 0.
RESUMO:
𝑓(𝑥) 𝐒𝐞 𝒎 ≠ 𝟎 ⟹ 𝑦 = 𝑚𝑥 + 𝑏 é AO
𝑙𝑖𝑚 = 𝑚{ ; 𝒎 𝐞 𝒃 ≠ ±∞
𝐀𝐎: 𝑦 = 𝑚𝑥 + 𝑏{ 𝑥→±∞ 𝑥 𝐒𝐞 𝒎 = 𝟎 ⟹ 𝑦 = 𝑏 é AH
ۖ
𝑙𝑖𝑚 [𝑓(𝑥) − 𝑚𝑥] = 𝑏
ANV 𝑥→±∞
𝐀𝐇: lim 𝑓(𝑥) = 𝑏, sendo 𝑏 ∈ ℝ
ۖ 𝑥→±∞
{𝐀 𝐀𝐎 𝐞 𝐀𝐇 não existem em simultâneo, ou seja, se a função possui 𝐀𝐎, ela não possui 𝐀𝐇 , e vice versa.

2023/2024
25
EXEMPLO 10:
𝑥 2 +1
1. Calcule a assímptota vertical da curva 𝑓(𝑥) = .
𝑥−1
Resolução:
𝑫𝒇 : 𝑥 − 1 ≠ 0 ⟹ 𝑥 ≠ 1.
𝑥 2 + 1 12 + 1 2
lim 𝑓(𝑥) = lim = = =∞
𝑥→1 𝑥→1 𝑥 − 1 1−1 0
Portanto, a recta 𝑥 = 1 é uma assímptota vertical da curva dada.
𝑥 2 +1
2. Calcule a assímptota horizontal da curva 𝑓(𝑥) = 𝑥 2 −1.
0
Resolução:
∞ 0
∞ 1 1
𝑥2 + 1 𝑥 2 (1 + 2 ) 1+ 2
lim 𝑓(𝑥) = lim 2 = lim 𝑥 = lim 𝑥 =1
𝑥→±∞ 𝑥→±∞ 𝑥 − 1 𝑥→±∞ 2 1 𝑥→±∞ 1
𝑥 (1 − 2 ) 1− 2
𝑥 𝑥
Logo, a recta 𝑦 = 1 é uma assímptota horizontal da curva dada.

2023/2024
26  Limites das funções logarítmicas e exponenciais
 Propriedades
Se 𝒂 for a base, temos:
 lim ln 𝑥 = +∞
1) Se 𝒂 > 𝟏 𝑥→+∞
 lim log 𝑎 𝑥 = +∞  lim+ ln 𝑥 = −∞

𝑥→+∞ 𝑥→0
 lim+ log 𝑎 𝑥 = −∞
𝑥→0
2) Se 𝟎 < 𝒂 < 𝟏
 lim log 𝑎 𝑥 = −∞
𝑥→+∞
 lim+ log 𝑎 𝑥 = +∞
𝑥→0
a>1 0<a<1
f(x) é decrescente e Im=IR
Função logarítmica
3) Se 𝒂 > 𝟏  lim 𝑒 𝑥 = +∞
𝑥→+∞
 lim 𝑎 𝑥 = +∞
𝑥→+∞
 lim 𝑒 𝑥 = 0
𝑥 𝑥→−∞
 lim 𝑎 = 0
𝑥→−∞
4) Se 𝟎 < 𝒂 < 𝟏  lim 𝑒 −𝑥 = 0

𝑥→+∞
 lim 𝑎 𝑥 = 0  lim 𝑎−𝑥 = +∞

𝑥→+∞ 𝑥→−∞
 lim 𝑎 𝑥 = +∞
𝑥→−∞

2023/2024
27 Função exponencial

2023/2024
28 2. CONTINUIDADE DE FUNÇÕES
 Continuidade
O que se entende por fenómeno contínuo?
Cada ser humano apresenta uma ideia intuitiva de continuidade.
Se pedíssemos a uma criança para desenhar numa folha o tempo,

possivelmente ela iria desenhar uma linha, sem interrupções.
Haverá alguma relação entre a continuidade e o dia-a-dia?
São diversas as ciências que recorrem à continuidade para

progredirem nos seus estudos. Normalmente este conceito está mais
direccionado para o ramo das ciências exactas tais como a
Matemática, a Física, a Biologia, a Química entre outras.
Perante as mais variadas situações, o Homem depara-se

constantemente com situações de continuidade.
O simples facto de “correr sangue nas nossas veias” é sinónimo de

continuidade, pois à partida que tal deixa de ser feito, a
continuidade é quebrada. Um exemplo, muito comum no nosso dia-a-dia é a
representação do horizonte, pois este é algo infinito, mas também contínuo.
 Estudo da Continuidade
O sinónimo que caracteriza o termo “Continuidade”, segundo

diversos dicionários, é algo que sofre de ausência de interrupção,
ou seja, em linguagem corrente significa que “não é interrompido”
ou “não está dividido em partes”.

2023/2024
29
SEGUNDO O MATEMÁTICO DESCARTES (1596 – 1650), uma função diz-se
contínua quando se consegue desenhar um gráfico “sem nunca ter levantado o lápis do
papel”.
Graficamente:
Função Contínua

2023/2024
30 Função Descontínua

2023/2024
31 2.1. Definição
Seja 𝑓(𝑥) uma função de domínio 𝐷 ⊂ ℝ e 𝒂 um valor 𝐷. Dizemos que

𝑓(𝑥) é contínua em 𝒂 se: lim 𝑓(𝑥) = 𝑓(𝑎).
𝑥→𝑎
Em decorrência da definição, dizemos que uma função 𝑓(𝑥) é contínua

em 𝒂 nas seguintes condições:
1. Existe 𝑓(𝑎)
2. Existe 𝑙𝑖𝑚 𝑓(𝑥)
𝑥→𝑎
3. 𝑙𝑖𝑚 𝑓(𝑥) = 𝑓(𝑎)

𝑥→𝑎
Observação: Caso uma das três condições impostas para que a

função seja contínua em 𝒂 não venha a ocorrer, dizemos então que
ela é descontínua (não é contínua) em 𝒂.
Casos há em que para determinarmos o limite de uma função quando

𝒙 → 𝒂 temos que recorrer aos limites laterais e portanto a
definição pode ser dada da forma seguinte:

2023/2024
32
1. Existe 𝑓(𝑎)
2. Existe 𝑙𝑖𝑚 𝑓(𝑥) ⇔ 𝑙𝑖𝑚− 𝑓(𝑥) = 𝑙𝑖𝑚+ 𝑓(𝑥)
3. 𝑙𝑖𝑚 𝑓(𝑥) = 𝑓(𝑎)

𝑥→𝑎
EXEMPLO 11:
1. Verifique se a função 𝑓(𝑥) = 𝑥 3 − 2𝑥, é contínua no ponto 𝑥 = 2.
Resolução: Obs.: Neste caso, não é necessário

recorrer aos limites laterais para
i. 𝑓(2) = 23 − 2 ∙ 2 = 8 − 4 = 4, existe.
mostrar a existência do limite quando 𝑥
ii. lim 𝑓(𝑥) = lim(𝑥 3 − 2𝑥) = 23 − 2 ∙ 2 = 8 − 4 = 4 tende para 2 da função 𝑓(𝑥) = 𝑥 3 − 2𝑥

𝑥⟶2 𝑥→2
iii. lim 𝑓(𝑥) = 𝑓(2) = 4

𝑥→2
Portanto, a função é contínua no ponto 𝑥 = 2.
𝑥 + 3 , 𝑠𝑒 𝑥 ≠ 1
2. Verifique se a função 𝑓(𝑥) = { , é contínua no ponto 𝑥 = 1
2 , 𝑠𝑒 𝑥 = 1
Resolução:
Obs.: Neste caso, não é necessário
i. 𝑓(1) = 2, existe. recorrer aos limites laterais para

mostrar a existência do limite quando
ii. lim 𝑓(𝑥) = lim(𝑥 + 3) = 1 + 3 = 4 𝑥 tende para 1 da função dada.
𝑥→1 𝑥→1
iii.lim 𝑓(𝑥) ≠ 𝑓(1)

𝑥→1
Portanto, a função não é contínua no ponto 𝑥 = 1.

2023/2024
𝑥+3 , 𝑠𝑒 𝑥 ≤ 2
33 3. Verifique se a função 𝑓(𝑥) = { , é contínua no ponto 𝑥 = 2.
3𝑥 − 1 , 𝑠𝑒 𝑥 > 2
Resolução:
i. 𝑓(2) = 2 + 3 = 5, existe.
ii. ∃ lim 𝑓(𝑥) ⇔ lim− 𝑓(𝑥) = lim+ 𝑓(𝑥)

𝑥→2 𝑥→2 𝑥→2
lim 𝑓(𝑥) = lim− (𝑥 + 3) = 2 + 3 = 5

𝑥→2− 𝑥→2
} ⇒ ∃ lim 𝑓(𝑥) = 5
lim+ 𝑓(𝑥) = lim+ (3𝑥 − 1) = 3 ∙ 2 − 1 = 6 − 1 = 5 𝑥→2
𝑥→2 𝑥→2
iii.lim 𝑓(𝑥) = 𝑓(2) = 5

𝑥→2
𝑥+2 , 𝑠𝑒 𝑥 ≤ 2
4. Verifique se a função 𝑓(𝑥) = { , é contínua no ponto 𝑥 = 2.
2−𝑥 , 𝑠𝑒 𝑥 > 2
Resolução:
i. 𝑓(2) = 2 + 2 = 4, existe.
𝑥→2 𝑥→2 𝑥→2
lim 𝑓(𝑥) = lim− (𝑥 + 2) = 2 + 2 = 4

𝑥→2− 𝑥→2
} ⇒ ∄ lim 𝑓(𝑥)
lim+ 𝑓(𝑥) = lim+ (2 − 𝑥) = 2 − 2 = 0 𝑥→2
𝑥→2 𝑥→2
Logo, a função não é contínua no ponto 𝑥 = 2, ou seja é descontínua no ponto 𝑥 = 2.
5. Determinar 𝑚 (𝑚 ∈ ℝ), de modo que a função
𝑥 2 − 4𝑥 + 3, 𝑠𝑒 𝑥 ≠ 2
𝑓(𝑥) = { seja contínua em 𝑥 = 2.
2𝑚 + 1 , 𝑠𝑒 𝑥 = 2
Resolução:
i. 𝑓(2) = 2𝑚 + 1
ii. lim 𝑓(𝑥) = lim (𝑥 2 − 4𝑥 + 3) = 22 − 4 ∙ 2 + 3 = 4 − 8 + 3 = −1

𝑥→2 𝑥→2

2023/2024
34 iii.Para que 𝑓(𝑥) seja contínua em 𝑥 = 2, devemos ter: lim 𝑓(𝑥) = 𝑓(2) ⇒
𝑥→2
−1 = 2𝑚 + 1 ⇒ 2𝑚 = −2 ⇒ 𝑚 = −1
Logo, 𝑓(𝑥) é contínua em 𝑥 = 2, se 𝑚 = −1.
6. Determinar 𝑘 (𝑘 ∈ ℝ), de modo que a função
7𝑥 − 2, 𝑠𝑒 𝑥 ≤ 1
𝑘𝑥 2 , 𝑠𝑒 𝑥 > 1
Resolução:
i. 𝑓(1) = 7 ∙ 1 − 2 = 7 − 2 = 5, existe.

𝑥→1 𝑥→1 𝑥→1
lim 𝑓(𝑥) = lim−(7𝑥 − 2) = 7 ∙ 1 − 2 = 7 − 2 = 5

𝑥→1− 𝑥→1
lim+ 𝑓(𝑥) = lim+𝑘𝑥 2 = 𝑘 ∙ 12 = 𝑘 ∙ 1 = 𝑘
𝑥→1 𝑥→1
Para que exista o limite de 𝑓(𝑥) quando 𝑥 tende para 1, é necessário e

suficiente que: lim− 𝑓(𝑥) = lim+ 𝑓(𝑥) ⇒ 5 = 𝑘 ⇔ 𝑘 = 5
𝑥→1 𝑥→1
Portanto, 𝑓(𝑥) é contínua em 𝑥 = 1, se 𝑘 = 5.
7. Determinar 𝑘 (𝑘 ∈ ℝ), de modo que a função
𝑘𝑥 2 , 𝑠𝑒 𝑥 ≤ 2
2𝑥 + 𝑘 , 𝑠𝑒 𝑥 > 2
Resolução:
i. 𝑓(2) = 𝑘 ∙ 22 = 𝑘 ∙ 4 = 4𝑘

𝑥→2 𝑥→2 𝑥→2
lim 𝑓(𝑥) = lim− 𝑘𝑥 2 = 𝑘 ∙ 22 = 𝑘 ∙ 4 = 4𝑘

𝑥→2− 𝑥→2
lim+ 𝑓(𝑥) = lim+(2𝑥 + 𝑘) = 2 ∙ 2 + 𝑘 = 4 + 𝑘
𝑥→2 𝑥→2
Para que exista o limite de 𝑓(𝑥) quando 𝑥 tende para 2, é necessário e

suficiente que: lim− 𝑓(𝑥) = lim+ 𝑓(𝑥) ⇒ 4𝑘 = 4 + 𝑘 ⇒ 4𝑘 − 𝑘 = 4 ⇒
𝑥→2 𝑥→2

2023/2024
4
35 ⟹ 3𝑘 = 4 ⇒ 𝑘 =
3
4
Portanto, 𝑘 = 3.
8. Estude a continuidade da função nos pontos indicados.
𝑥, 𝑠𝑒 𝑥 > 1
𝑓(𝑥) = {2𝑥 − 1, 𝑠𝑒 0 ≤ 𝑥 ≤ 1 , em 𝑥 = 0 e 𝑥 = 1
−1 + 𝑥, 𝑠𝑒 𝑥 < 0
Resolução:
Analisando a continuidade nos pontos 𝑥 = 0 e 𝑥 = 1.
i. 𝑓(0) = 2 ∙ 0 − 1 = 0 − 1 = −1 e 𝑓(1) = 2 ∙ 1 − 1 = 2 − 1 = 1, existe.
ii. ∃ lim 𝑓(𝑥) ⇔ lim− 𝑓(𝑥) = lim+ 𝑓(𝑥) e ∃ lim 𝑓(𝑥) ⇔ lim− 𝑓(𝑥) = lim+ 𝑓(𝑥)
𝑥→0 𝑥⟶0 𝑥⟶0 𝑥→1 𝑥⟶1 𝑥⟶1
lim 𝑓(𝑥) = lim−(−1 + 𝑥) = −1 + 0 = −1

𝑥⟶0− 𝑥⟶0
} ⇒ ∃ 𝐥𝐢𝐦 𝒇(𝒙) = −𝟏
lim+ 𝑓(𝑥) = lim+(2𝑥 − 1) = 2 ∙ 0 − 1 = 0 − 1 = −1 𝒙→𝟎
𝑥⟶0 𝑥⟶0
lim 𝑓(𝑥) = lim−(2𝑥 − 1) = 2 ∙ 1 − 1 = 2 − 1 = 1

𝑥⟶1− 𝑥⟶1
} ⇒ ∃ 𝐥𝐢𝐦 𝒇(𝒙) = 𝟏
lim+ 𝑓(𝑥) = lim+ 𝑥 = 1 𝒙→𝟏
𝑥⟶1 𝑥⟶1
iii. lim 𝑓(𝑥) = 𝑓(0) = −1 e lim 𝑓(𝑥) = 𝑓(1) = 1

𝑥→0 𝑥→1
Portanto, a função é contínua nos pontos 𝑥 = 0 e 𝑥 = 1.
𝑥 3 +𝑥 2 −𝑥
2 −6𝑥
, 𝑠𝑒 𝑥 < 0
ۖ 1𝑥
9. Verifique se a função 𝑓(𝑥) = , 𝑠𝑒 𝑥 = 0, é contínua no ponto 𝑥 = 0.
6
ۖ √𝑥+9 − 3 , 𝑠𝑒 𝑥 > 0
{ 𝑥
Resolução:
i.
1
𝑓(0) = 6, existe.

𝑥→0 𝑥→0 𝑥→0

2023/2024
𝑥3 + 𝑥2 − 𝑥 𝑥(𝑥 2 + 𝑥 − 1) 𝑥2 + 𝑥 − 1 1
36 lim− 𝑓(𝑥) = lim− = lim = lim =
𝑥→0 𝑥→0 𝑥 2 − 6𝑥 𝑥→0− 𝑥(𝑥 − 6) 𝑥→0− 𝑥−6 6
√𝑥+9 – 3 (√𝑥+9 – 3)(√𝑥+9 + 3) 𝑥+9−9
Lim+ 𝑓(𝑥) = lim+ = lim+ = lim+ 𝑥(√𝑥+9 + 3) =
𝑥→0 𝑥→0 𝑥 𝑥→0 𝑥(√𝑥+9 + 3) 𝑥→0
𝑥 1 1
= lim+ 𝑥(√𝑥+9 + 3) = lim+ =6
𝑥→0 𝑥→0 √𝑥+9 + 3
1
Como, lim− 𝑓(𝑥) = lim+ 𝑓(𝑥) ⟹ ∃ lim 𝑓(𝑥) = 6
𝑥→0 𝑥→0 𝑥→0
iii.
1
lim 𝑓(𝑥) = 𝑓(0) = 6.
𝑥→0
 Definição: Dado um ponto 𝒂 do domínio de uma função 𝑓. Dizemos que 𝑓 é

contínua à direita de 𝒂 se:
𝐥𝐢𝐦 𝒇(𝒙) = 𝒇(𝒂)

𝒙→𝒂+
E, Dizemos que 𝑓 é contínua à esquerda de 𝒂 se:
𝐥𝐢𝐦 𝒇(𝒙) = 𝒇(𝒂)

𝒙→𝒂−
 Definição: Dizemos que uma função 𝑓 é contínua em um intervalo fechado

[𝑎; 𝑏] se 𝑓 é contínua no intervalo aberto (𝑎; 𝑏) ou ]𝑎; 𝑏[ e se é contínua à direita
de 𝒂 e à esquerda de 𝒃.
Teorema 3: Se 𝑓 e 𝑔 forem contínuas em um ponto 𝒂 e se 𝒌 for uma constante,

então as seguintes funções também são contínuas em 𝒂:
𝒇
1) 𝒇 ± 𝒈 2) 𝒇 ∙ 𝒈 3) , sendo 𝑔(𝑎) ≠ 0 4) 𝒌 ∙ 𝒇
𝒈
Teorema 4: Toda função é contínua para todo número de seu domínio.

2023/2024
37 EXERCÍCIOS PROPOSTOS
1. Verifique a existência dos limites, nos pontos indicados.
𝑥 2 − 5, 𝑠𝑒 𝑥 < 3
a) 𝑓(𝑥) = { , no valor 𝑥 = 3 Nota: Por definição de módulo
√𝑥 + 13, 𝑠𝑒 𝑥 ≥ 3
de um número real, temos:
2
3𝑥 − 2, 𝑝𝑎𝑟𝑎 𝑥 ≥ 3 2 −𝑥, 𝑠𝑒 𝑥 < 0
b) 𝑓(𝑥) = { , no valor 𝑥 = 3 |𝑥| = {
2 𝑥, 𝑠𝑒 𝑥 ≥ 0
4 − 6𝑥, 𝑝𝑎𝑟𝑎 𝑥 < 3
2𝑥 + 1, 𝑠𝑒 𝑥 > 1
c) 𝑓(𝑥) = { , no valor 𝑥 = 1
𝑥 − 3, 𝑠𝑒 𝑥 ≤ 1
4 − 𝑥 2 , 𝑠𝑒 𝑥 ≥ 0
d) 𝑓(𝑥) = { , no valor 𝑥 = 0
3 − 𝑥, 𝑠𝑒 𝑥 < 0
𝑥2, 𝑠𝑒 𝑥 > 1
e) 𝑓(𝑥) = { , no valor 𝑥 = 1
2𝑥 − 1, 𝑠𝑒 𝑥 ≤ 1
|𝑥|
f) 𝑓(𝑥) = , para 𝑥 = 0
𝑥
𝑥 3 −2𝑥 2 −5𝑥+6
, 𝑠𝑒 𝑥 < 3
𝑥−3
g) 𝑓(𝑥) = { , no valor 𝑥 = 3
√𝑥+1 − 1
, 𝑠𝑒 𝑥 ≥ 3
𝑥+2
3 − √1 − 𝑥 , 𝑠𝑒 𝑥 ≤ 0
h) 𝑓(𝑥) = { 𝑥 , no valor 𝑥 = 0
𝑒2 + 1 , 𝑠𝑒 𝑥 > 0
2. Verifique, em cada caso, se a função 𝑓(𝑥) é contínua no valor

dado.
2, 𝑠𝑒 𝑥 < 5
a) 𝑓(𝑥) = { , no valor 𝑥 = 5
3, 𝑠𝑒 𝑥 ≥ 5
𝑥2, 𝑝𝑎𝑟𝑎 𝑥 ≤ 1
b) 𝑓(𝑥) = { , no valor 𝑥 = 1
3𝑥 − 2, 𝑝𝑎𝑟𝑎 𝑥 > 1
𝑥 + 3, 𝑠𝑒 𝑥 ≠ 1
c) 𝑓(𝑥) = { , no valor 𝑥 = 1
2 , 𝑠𝑒 𝑥 = 1
2𝑥
d) 𝑓(𝑥) = 𝑥−2, no valor 𝑥 = 2
𝑥 2 +𝑥−2
, 𝑠𝑒 𝑥 > 1
e) 𝑓(𝑥) = { 𝑥−1 , no valor 𝑥 = 1
2 − 𝑥 , 𝑠𝑒 𝑥 ≤ 1
𝑥 2 +𝑥−2
, 𝑠𝑒 𝑥 > 1
f) 𝑓(𝑥) = { 𝑥−1 , no valor 𝑥 = 1
𝑥 + 2 , 𝑠𝑒 𝑥 ≤ 1
𝑥 2 −4
, 𝑠𝑒 𝑥 ≠ 2
g) 𝑓(𝑥) = { 𝑥−2 , no valor 𝑥 = 2
3 , 𝑠𝑒 𝑥 = 2

2023/2024
𝑥 2 −4
38 , 𝑠𝑒 𝑥 ≠ 2
h) 𝑓(𝑥) = { 𝑥−2 , no valor 𝑥 = 2
4 , 𝑠𝑒 𝑥 = 2
𝑥 2 −5𝑥+4
, 𝑠𝑒 𝑥 ≠ 4
i) 𝑓(𝑥) = { 𝑥−4 , no valor 𝑥 = 4
5, 𝑠𝑒 𝑥 = 4
√4+𝑥 − √4−𝑥
, 𝑠𝑒 𝑥 ≠ 0
j) 𝑓(𝑥) = {1 𝑥 , no valor 𝑥 = 0
, 𝑠𝑒 𝑥 = 0
3
8−𝑥
, 𝑠𝑒 𝑥 < 8
k) 𝑓(𝑥) = { 3√𝑥 − 2 , no valor 𝑥 = 8
3 − 2𝑥, 𝑠𝑒 𝑥 ≥ 8
1 − 𝑥 2 , 𝑠𝑒 𝑥 ≤ 1
l) 𝑓(𝑥) = {𝑥 − 1, 𝑠𝑒 1 < 𝑥 < 2 , no valor 𝑥 = 1 e 𝑥 = 2
1, 𝑠𝑒 𝑥 ≥ 2
2𝑥 + 3, 𝑠𝑒 𝑥 ≤ 1
m) 𝑓(𝑥) = { 8 − 3𝑥, 𝑠𝑒 1 < 𝑥 < 3 , no valor 𝑥 = 1 e 𝑥 = 3
𝑥 + 3, 𝑠𝑒 𝑥 ≥ 3
𝑥, 𝑠𝑒 𝑥>1
n) 𝑓(𝑥) = { 2𝑥 − 1, 𝑠𝑒 0 ≤ 𝑥 ≤ 1 , no valor 𝑥 = 0 e 𝑥 = 1
−1 + 𝑥, 𝑠𝑒 𝑥 < 0
3. Determine o valor de 𝒂, em cada caso, para que 𝑓(𝑥) seja contínua

no valor considerado:
𝑥 2 −4
, 𝑠𝑒 𝑥 ≠ 2
a) 𝑓(𝑥) = { 𝑥−2 , no valor 𝑥 = 2
𝑎 , 𝑠𝑒 𝑥 = 2
7𝑥 − 6, 𝑠𝑒 𝑥 < 2
b) 𝑓(𝑥) = { , no valor 𝑥 = 2
2𝑎 , 𝑠𝑒 𝑥 ≥ 2
1 + 𝑥2, 𝑠𝑒 𝑥 < 0
c) 𝑓(𝑥) = { , no valor 𝑥 = 0
𝑎 + 3𝑥 , 𝑠𝑒 𝑥 ≥ 0
𝑎2 𝑥 2 , 𝑠𝑒 𝑥 ≤ 2
d) 𝑓(𝑥) = { , no valor 𝑥 = 2
1−𝑎, 𝑠𝑒 𝑥 > 2
2𝑎 + 𝑥, 𝑠𝑒 𝑥 ≥ 2
e) 𝑓(𝑥) = { 𝑥 2 −2𝑥 , no valor 𝑥 = 2
, 𝑠𝑒 𝑥 < 2
𝑥 2 −5𝑥+6
3𝑥 − 1, 𝑠𝑒 𝑥 ≤ 2
f) 𝑓(𝑥) = { , no valor 𝑥 = 2
2𝑥 − 𝑎 , 𝑠𝑒 𝑥 > 2
𝑎 + 2𝑥, 𝑠𝑒 𝑥 = −3
g) 𝑓(𝑥) = {𝑥 2 −9 , no valor 𝑥 = −3
, 𝑠𝑒 𝑥 ≠ −3
𝑥+3
𝑥 2 −4
, 𝑠𝑒 𝑥 ≠ −2
h) 𝑓(𝑥) = { 𝑥+2 , no valor 𝑥 = −2
𝑎 , 𝑠𝑒 𝑥 = −2

2023/2024
𝑥 2 −4
39 , 𝑠𝑒 𝑥 > −2
i) 𝑓(𝑥) = {𝑥 2 +2𝑥 , no valor 𝑥 = −2
𝑥+𝑎, 𝑠𝑒 𝑥 ≤ −2
3𝑥 − 1, 𝑠𝑒 𝑥 < 1
j) 𝑓(𝑥) = { 𝑎2 − 𝑎, 𝑠𝑒 𝑥 = 1 , no valor 𝑥 = 1
𝑥 + 1, 𝑠𝑒 𝑥 > 1
𝑥 2 −4
, 𝑠𝑒 𝑥 > −2
k) 𝑓(𝑥) = {𝑥 2 +2𝑥 , no valor 𝑥 = −2
𝑥+𝑎, 𝑠𝑒 𝑥 ≤ −2
15𝑠𝑒𝑛𝑥
, 𝑠𝑒 𝑥 ≠ 0
l) 𝑓(𝑥) = { 𝑥 , no valor 𝑥 = 0
𝑎2 + 2𝑎 , 𝑠𝑒 𝑥 = 0
𝑠𝑒𝑛2𝑥
− 2, 𝑠𝑒 𝑥 ≠ 0
m) 𝑓(𝑥) = { 𝑥 , no valor 𝑥 = 0
0 , 𝑠𝑒 𝑥 = 0
𝑥𝑒 𝑥−1 , 𝑠𝑒 𝑥 ≤ 1
n) 𝑓(𝑥) = { , no valor 𝑥 = 1
ln 𝑘𝑥 , 𝑠𝑒 𝑥 > 1
EXERCÍCIOS PROPOSTOS
𝑥 3 +𝑥 2 −𝑥
2 −6𝑥
, 𝑠𝑒 𝑥 < 0
ۖ 1𝑥
1. Verifique se a função 𝑓(𝑥) = 6
, 𝑠𝑒 𝑥 = 0 , é contínua no ponto 𝑥 = 0.
ۖ √𝑥+9 − 3 , 𝑠𝑒 𝑥 > 0
{ 𝑥
2. Considere a função g definida por

2x 2 + 2x − 4
2−4
, se x < −2
g(x) = x
2β − 12
, se x ≥ −2
{ β+1
para β ∈ ℝ ∖ {−1}. Determine o valor de β para o qual a função g é contínua em

x = −2.
3. Considere a função g definida em ℝ, por

x
se x < 0
ۖ 3 − √9 − x
g(x) = 6 se x = 0
ۖ5x + ln(x + 1) se x > 0
{ x

2023/2024
Estude a continuidade de g em x = 0.
40
4. Considere a função w, de domínio ℝ, definida por

x 2 + 2x
se x < 0
ۖ x3 + x
w(x) = 2 se x = 0
2
ۖ3x − xln(x + 1) se x > 0
{ x2
Averigue se w é contínua em x = 0. Justifique a sua resposta.
5. Seja f a função, de domínio ℝ, definida por

3x 2 + 6x
se x < 0
ۖ 3x 3 + 3x
f(x) = 2 se x = 0
2
ۖ4x − xln(2x + 1) se x > 0
{ x2
Averigue se f é contínua em x = 0. Justifique a sua resposta.
6. Para um certo valor de α e para um certo valor β, é contínua em x = 0 a função h,

definida por
e2x − 1
se x < 0
ۖ x
h(x) = α se x = 0
ۖβ − ln(x + 1) se x > 0
{ x
Determine os valores de α e de β.
2 − 2e2+x , se x < −2
7. Considere a função g(x) = { 2
(x + 1) − 1 , se x ≥ −2
Prove que g é contínua em x = −2.
1−x
8. Considere a função f(x) = { e , se x < 1
1 + 4 ln x , se x ≥ 1
Prove que f é contínua em x = 1.

2023/2024
41 9. Seja 𝑓 uma função de domínio ℝ definida por

𝑒𝑥, 𝑠𝑒 𝑥 ≤ 0
𝑓(𝑥) = {
𝑥 + 1, 𝑠𝑒 𝑥 > 0
Justifique que 𝑓 é contínua no ponto 𝑥 = 0.
x2 + 1 , se x ≤ 0
10. Considere a função f(x) = { 1 , se 0 < x < e
ln x , se x ≥ e
Estude a continuidade de f em x = 0 e x = e.

2023/2024
42 ANEXO
CONCEITO DE LIMITE
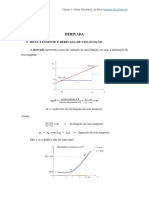
O conceito de limite é fundamental no cálculo diferencial, um

campo da Matemática que iniciou – se no século XVII sendo bastante
produtivo em resultados e aplicações em várias áreas do
conhecimento, como a Física, a Engenharia, a Economia, a Geologia,
a Astronomia, a Biologia, entre outras.
Com o desenvolvimento do cálculo diferencial, matemáticos como

Huygens (1629 – 1695), Newton (1642 – 1727) e Leibniz (1646 –
1716) tiveram papel marcante. Buscando aperfeiçoar a conceituação
de limites, tiveram destaques as contribuições de d’ Alembert
(1717 – 1783) e de Cauchy ( 1789 – 1857).
Na Matemática atual, as definições de convergência, divergência,

continuidade, derivada e integral estão baseadas no conceito de
limite.
Noção Intuitiva de Limites
Exemplos:
a) Considerando uma região quadrada de área igual a 1.

Inicialmente vamos colorir a metade do quadrado.
1
Parte colorida = 2 da figura
Após, vamos pintar a metade da região e mais metade do que restou.
1 1 3
Parte colorida = 2 + 4 = 4 da figura

2023/2024
43
No próximo , vamos colorir o que havia sido colorido e mais metade

do que restou:
1 1 1 7
Parte colorida = 2 + 4 + 8 = 8 da figura
E assim, sucessivamente e indefinidamente, a área da região

colorida resultante vai tendendo a 1. Dizemos, então, que o limite
desse desenvolvimento, quando o número de momentos tende ao
infinito, é colorir a figura toda, ou seja, obter uma área colorida
igual a 1.
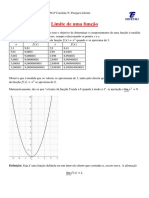
b) Seja a função f(x) = 2x + 1. Vamos associar valores de x que

se aproximem de 1, pela sua direita (valores maiores que 1) e pela
esquerda (valores menores que 1) e calcular o valor correspondente
de y.
Observamos que quando x tende para 1, y tende para 3 e o limite

da função é 3.
lim 2𝑥 + 1 = 3
𝑥→1
De maneira geral, escrevemos lim 𝑓(𝑥) = 𝑏, se, quando x se aproxima

𝑥→𝑎
de a ( x →a), f (x) se aproxima de b ( f(x) →b).


Manual de Apoio - Limites de Funções e Continuidade de Funções

Enviado por

Dados do documento

Título original

Direitos autorais

Formatos disponíveis

Compartilhar este documento

Compartilhar ou incorporar documento

Opções de compartilhamento

Você considera este documento útil?

Este conteúdo é inapropriado?

Direitos autorais:

Formatos disponíveis

Manual de Apoio - Limites de Funções e Continuidade de Funções

Enviado por

Direitos autorais:

Formatos disponíveis

2023/2024

TEMA:Limites Funções e Continuidade de Funções

1. LIMITE DE UMA FUNÇÃO

Diz-se que o limite da função f(x) quando x tende a “a” é igual

Se para todo e qualquer número 𝜀 > 0, existir 𝛿 > 0 tal que se

Definição de Limite (Segundo Heine)

Seja 𝑓(𝑥) uma função de variável real e, 𝒂 e 𝒃 constantes

Definição de Limite (Segundo Cauchy)

Sendo 𝒂 e 𝐿 números reais, diz-se que uma função 𝑓(𝑥) tende

𝐥𝐢𝐦 𝒇(𝒙) = 𝑳 ⇔ ∀𝜺 > 𝟎, ∃𝜹 > 𝟎 / se 𝟎 < |𝒙 − 𝒂| < 𝜹 ⇒ |𝒇(𝒙) − 𝑳| < 𝜺.

Dionísio A. Palma / 921 935 906 / 951 962 371 / dionisiopalma00@gmail.com

Se substituirmos estes valores na função dada obtemos uma sucessão de valores de 𝑦,

EXEMPLO 2: Aplicando a definição de limite segundo Cauchy, mostre

lim 2𝑥 + 3 = 5 ⟺ ∀𝜖 > 0, ∃𝛿 > 0?/ se 0 < |𝑥 − 1| < 𝛿 ⟹ |𝑓(𝑥) − 5| < 𝜖.

Como, |𝑓(𝑥) − 5| = |2𝑥 + 3 − 5| = |2𝑥 − 2| = |2(𝑥 − 1)| = |2| ∙ |𝑥 − 1| =

Dionísio A. Palma / 921 935 906 / 951 962 371 / dionisiopalma00@gmail.com

lim [𝑘 ∙ 𝑓(𝑥)] = 𝑘 ∙ lim 𝑓(𝑥)

lim [𝑓(𝑥) ± 𝑔(𝑥)] = lim 𝑓(𝑥) ± lim 𝑔(𝑥)

lim [𝑓(𝑥) ∙ 𝑔(𝑥)] = lim 𝑓(𝑥) ∙ lim 𝑔(𝑥)

lim [ln 𝑓(𝑥)] = ln [lim 𝑓(𝑥)]

9. lim cos(𝑓(𝑥)) = cos (lim 𝑓(𝑥))

Dionísio A. Palma / 921 935 906 / 951 962 371 / dionisiopalma00@gmail.com

4 10. lim sen(𝑓(𝑥)) = sen (lim 𝑓(𝑥))

12. lim 𝑃(𝑥) = 𝑃(𝑎), sendo 𝑃(𝑥) um polinómio.

1.3 Símbolos de Indeterminação

1.4 Algumas Operações Determinadas

b) 𝑘 × (±∞) = ∓∞, 𝑘 < 0

Dionísio A. Palma / 921 935 906 / 951 962 371 / dionisiopalma00@gmail.com

h) (−∞)𝑛 = +∞, 𝑛 ∈ ℕ, par e 𝑛 ≠ 0

OBSERVAÇÃO: Se 𝑓(𝑥) = 𝑃(𝑥) = Polinómio em x. Então, com

𝑓(𝑥) = 𝑃(𝑥) = 𝑎𝑛 𝑥 𝑛 + 𝑎𝑛−1 𝑥 𝑛−1 + ⋯ + 𝑎2 𝑥 2 + 𝑎1 𝑥 + 𝑎0 , vem:

Dionísio A. Palma / 921 935 906 / 951 962 371 / dionisiopalma00@gmail.com

4. 𝑎4 − 𝑏 4 = (𝑎2 − 𝑏 2 )(𝑎2 + 𝑏 2 ) = (𝑎 − 𝑏)(𝑎 + 𝑏)(𝑎2 + 𝑏 2 )

7. (𝑎 − 𝑏)3 = 𝑎3 − 3𝑎2 𝑏 + 3𝑎𝑏 2 − 𝑏 3

8. (𝑎 + 𝑏)3 = 𝑎3 + 3𝑎2 𝑏 + 3𝑎𝑏 2 + 𝑏 3

1.6 Limites Laterais

Se 𝑥 < 𝑎, convencionalmente, escreve-se 𝑥 → 𝑎− ; por analogia, se

Os números 𝑓(𝑎− ) = lim− 𝑓(𝑥) e 𝑓(𝑎+ ) = lim+ 𝑓(𝑥), chamam-se,

respectivamente, limite à esquerda da função 𝑓(𝑥) no ponto 𝒂, e

Para a existência do limite da função 𝒇(𝒙), sendo 𝒙 → 𝒂, é

𝒇(𝑎− ) = 𝒇(𝑎+ ) ⇔ 𝐥𝐢𝐦− 𝒇(𝒙) = 𝐥𝐢𝐦+ 𝒇(𝒙).

Dionísio A. Palma / 921 935 906 / 951 962 371 / dionisiopalma00@gmail.com

lim 𝑓(𝑥) ou lim 𝑓(𝑥)

∃ lim 𝑓(𝑥) ⟺ lim− 𝑓(𝑥) = lim+ 𝑓(𝑥)

lim 𝑓(𝑥) = lim−(𝑥 + 2) = 2 + 2 = 4

lim 𝑓(𝑥) = lim+(2 − 𝑥) = 2 − 2 = 0

Dionísio A. Palma / 921 935 906 / 951 962 371 / dionisiopalma00@gmail.com

∃ lim 𝑓(𝑥) ⟺ lim− 𝑓(𝑥) = lim+ 𝑓(𝑥).

lim 𝑓(𝑥) = lim−(𝑥 2 − 5) = 9 − 5 = 4

lim 𝑓(𝑥) = lim+ √𝑥 + 13 = √3 + 13 = √16 = 4

Como, lim− 𝑓(𝑥) = lim+ 𝑓(𝑥) logo, existe lim 𝑓(𝑥) = 4.

Obs.: Devemos recorrer aos limites laterais quando ao procurarmos 𝑥→𝑎

1.7 Cálculo de limites indeterminados

 Ao calcular-se o limite da razão de dois polinómios

Dionísio A. Palma / 921 935 906 / 951 962 371 / dionisiopalma00@gmail.com

9  As expressões irracionais se reduzem, em muitos casos, à

Dionísio A. Palma / 921 935 906 / 951 962 371 / dionisiopalma00@gmail.com

Calculemos os limites laterais: 𝑥 2 − 𝑥 + 6 22 − 2 + 6

Como os limites à esquerda e à direita de 𝟐 são diferentes,

Dionísio A. Palma / 921 935 906 / 951 962 371 / dionisiopalma00@gmail.com

√𝑥 − 1 (√𝑥 − 1)(√𝑥 + 1)(√2𝑥 + 3 + √5)

(𝑥 − 1)(√2𝑥 + 3 + √5) √2𝑥 + 3 + √5 2√5 √𝟓

(3 − 𝑥)4 − 16 (1 − 𝑥)(5 − 𝑥)((3 − 𝑥)2 + 4)